復雜儲層連通孔隙度評價與滲透率定量計算方法

李雄炎 秦瑞寶 曹景記 汪 鵬 劉小梅 平海濤

(中海油研究總院有限責任公司，北京 100028)

0 引言

常規砂巖儲層主要發育粒間孔，孔隙類型單一，儲層相對均質。而復雜儲層發育溶蝕孔、生物孔、晶間孔、鑄模孔、微裂縫等，孔隙類型多樣，孔隙結構復雜，非均質性強。復雜儲層中普遍存在孔隙度相近而滲透率(K)差異較大的現象。目前尚未見孔隙連通性的評價和連通孔隙度(φc)的計算模型等方面的研究成果。基于總孔隙度(φ)[1-3]、孔隙結構參數[4-7]計算滲透率的一系列方法在復雜儲層中均未獲得理想的效果。另外，在基于核磁共振測井的方法中，盡管針對孔徑組分、雙截止值、T2譜分別建立了滲透率評價方法[8-12]，但未能建立具有普適性的孔隙度指數模型及核磁共振T2模型。采用機器學習算法及地震曲率預測滲透率[13-16]并不適用于復雜儲層。在實際應用中，為了減小核磁共振T2模型的評價誤差，往往是基于適當的巖心實驗標定，選擇適用于不同類型儲層的孔隙度指數，但均未闡明孔隙度指數變化的根本原因。

針對上述問題，本文首先采用鑄體薄片、核磁共振、CT掃描成像等實驗方法求取巖心的連通孔隙度，再從巖石孔隙空間“連通”和“導電”的角度出發，以導電孔隙度(φf)為橋梁，建立連通孔隙度的計算模型，分析十二種不同類型巖石中連通孔隙度與總孔隙度的關系。基于連通孔隙度的計算模型，改進核磁共振T2模型，形成復雜儲層滲透率的定量計算方法。然后以石灰巖儲層為例，在相近孔隙度條件下，從不同類型巖石滲透率之間的差異出發，推導、建立孔隙度指數模型和適用于石灰巖儲層核磁共振T2模型。實際結果表明，基于孔隙度指數模型建立的核磁共振T2模型能更準確地評價石灰巖儲層的滲透率。因此，連通孔隙度模型、孔隙度指數模型及普適性的核磁共振T2模型對于復雜儲層連通孔隙度評價與滲透率定量計算具有一定的理論價值和實際意義。

1 連通孔隙度的實驗測定

在復雜儲層中，孔隙結構是滲透率的一個主控因素，連通孔隙度是決定滲透率大小的一個重要參數[17-22]。巖石內孔隙連通性可以通過鑄體薄片、核磁共振、CT掃描成像等實驗進行評價。其中，鑄體薄片實驗可以在平面上直觀顯示不同類型孔隙之間的連通性，但不能定量計算連通孔隙度； 核磁共振實驗可以定量計算連通孔隙度，但不能直觀顯示不同類型孔隙之間的連通性[21]； CT掃描成像實驗不僅可以在空間上直觀顯示不同類型孔隙之間的連通性，而且可以定量計算連通孔隙度[23-24]。

1.1 鑄體薄片實驗

兩塊白云巖巖心樣品的鑄體薄片如圖1所示。根據孔隙充填的程度可知，兩塊樣品的孔喉半徑、總孔隙度均相近，但連通性不同，導致滲透率存在較大差異。

盡管鑄體薄片可以在平面上直觀顯示兩塊樣品的連通孔隙度存在差異，但無法定量給出連通孔隙度的大小。

圖1 兩塊白云巖巖心樣品的鑄體薄片

1.2 核磁共振實驗

兩塊白云巖巖心樣品飽和時與驅替后的橫向弛豫時間T2譜如圖2所示。巖心樣品飽和時的核磁孔隙度可以認為是總孔隙度，驅替后的核磁孔隙度可以認為是不連通孔隙度，二者之差即為連通孔隙度。因此，巖心樣品1的連通孔隙度為2.62%，連通孔隙占比為59.82%； 巖心樣品2的連通孔隙度為0.69%，連通孔隙占比為15.83%。

盡管核磁共振實驗可以定量給出巖心樣品連通孔隙度的大小，但無法在平面上或空間上直觀顯示不同類型孔隙之間的連通性。

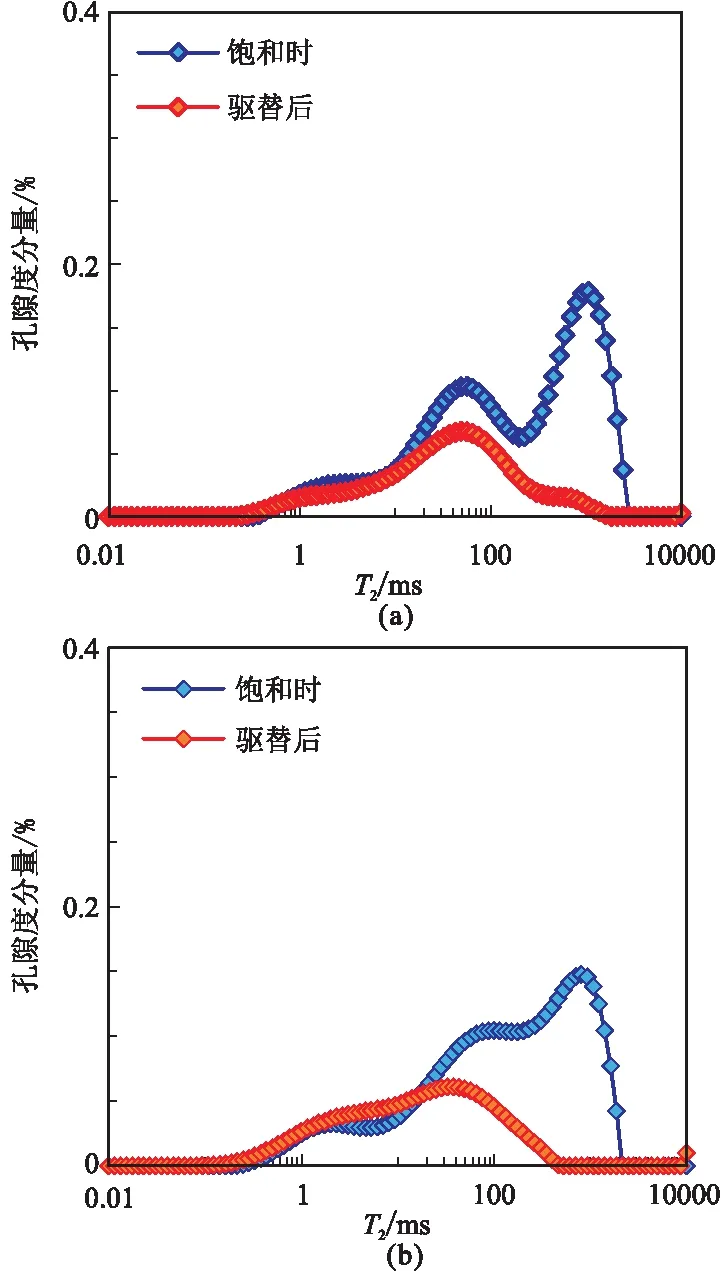
圖2 兩塊白云巖巖心樣品飽和時與驅替后的核磁共振橫向弛豫時間T2譜分布圖

1.3 CT掃描成像實驗

典型的X射線CT掃描成像布局如圖3所示。其中X射線源與探測器分別置于巖心樣品轉臺的兩側，X射線穿透放置在轉臺上的巖心樣品后被探測器接收，巖心樣品可以進行縱向、橫向平移或垂直升降運動。當巖心樣品縱向距X射線源越近，巖心樣品放大倍數越大，內部細節同時會被放大，因而圖像分辨率越高，可探測的區域越小； 相反，巖心樣品縱向距X射線源越遠，巖心樣品放大倍數越小，圖像分辨率越低，可探測區域越大。巖心樣品的橫向平移和垂直升降可用于改變掃描區域，但不改變圖像分辨率。將旋轉360°后所獲得的一系列投影圖像進行重構后，便可得到巖心樣品CT掃描的三維圖像。

通過鉆取巖心樣品、濾波降噪、二值化分割、孔隙填涂，重建巖心樣品的三維數字模型，并建立孔喉球棍(體)模型和孔隙連通(體)模型，可展示巖心樣品的三維內部結構(圖4、圖5)。

對比圖4h與圖5h可知，巖心樣品1的孔隙連通性明顯好于巖心樣品2。巖心樣品的CT掃描成果(表1)揭示，兩塊巖心樣品的總孔隙度、孔喉半徑、孔隙數量、孔隙體積均相近，但孔隙連通體積百分比和連通孔隙度的差異較大。

另外，由于鑄體薄片、核磁共振、CT掃描成像實驗中巖心樣品的尺寸相差甚大，且白云巖儲層非均質性強，因而不同方法所測定的連通孔隙度、總孔隙度之間存在著一定的差異。

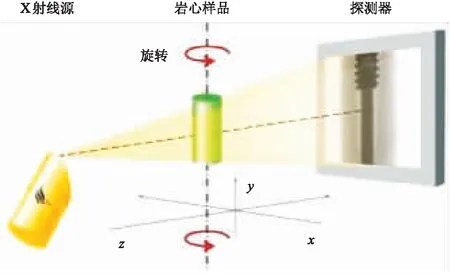
圖3 巖心樣品CT掃描成像布局圖

圖4 巖心樣品1的CT掃描成果圖

表1 巖心樣品的CT掃描成果

圖5 巖心樣品2的CT掃描成果圖(a)截取位置； (b)濾波降噪； (c)二值化分割； (d)孔隙填涂； (e)孔喉球棍體模型； (f)孔喉球棍模型； (g)孔隙連通體模型； (h)孔隙連通性模型

2 連通孔隙度的計算模型

鑄體薄片、核磁共振、CT掃描成像等實驗可以顯示巖石內連通孔隙的分布情況，但難以建立連通孔隙度的計算模型。

從“連通”的角度來看，巖石孔隙空間可以被分為連通孔隙和不連通孔隙； 從“導電”的角度來看，巖石孔隙空間則可以被分為導電孔隙和不導電孔隙。由于連通孔隙與導電孔隙所表征的孔隙空間是相同的，因此，可以認為連通孔隙度等于導電孔隙度。基于Maxwell方程，地層因素與導電孔隙度之間的關系為[25-29]

(1)

式中：F為地層因素；G、z為孔隙幾何形狀參數。

通過假設函數關系并設置相應的邊界條件之后[30]，可以得出

(2)

式中φs為不導電孔隙度。聯立式(1)、式(2)，便能得到

(3)

以(1-φ)/(F-1)為橫坐標、φ為縱坐標，可求取直線的斜率G。將其代入式(1)，便能求解導電孔隙度φf，從而得到連通孔隙度φc。

基于上述方法，本文分別計算了十二種巖性的連通孔隙度，并建立了總孔隙度與連通孔隙度之間的函數關系(表2)。

在十二種巖性中，連通孔隙度與總孔隙度的四種典型函數關系分別為線性、多項式、乘冪和指數(圖6)。由表2、圖6可知：①與礫巖相比，角礫巖磨圓度極低且分選很差，角礫巖的總孔隙度與連通孔隙度呈現更為復雜的函數關系； ②不同類型的巖石連通孔隙度與總孔隙度之間的函數關系存在較大差異，即使總孔隙度相近，連通孔隙度也會存在較大差異。這也就解釋了在一些巖石中，盡管總孔隙度相近，但滲透率卻存在較大差異，根本原因是連通孔隙度不同。

連通孔隙度主要與總孔隙度、巖石類型相關，因此復雜儲層連通孔隙度的計算模型為

φc=f(φ,L)

(4)

式中L代表巖石類型。

基于核磁共振、CT掃描實驗所測定的連通孔隙度，結合連通孔隙度與總孔隙度函數關系，可以綜合評價所計算連通孔隙度的準確性。

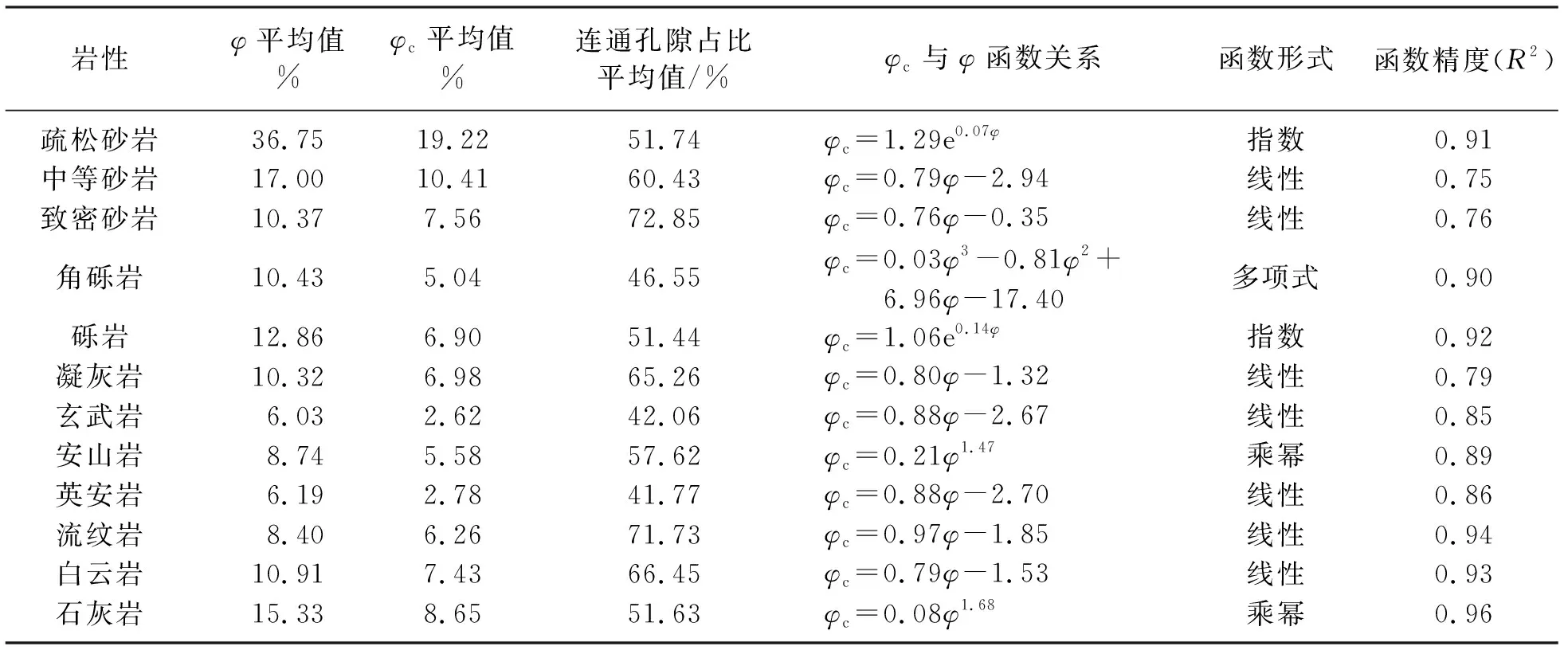
表2 十二種巖性的總孔隙度、連通孔隙度及它們之間的函數關系

圖6 四種典型的φc與φ函數關系(a)致密砂巖； (b)角礫巖； (c)礫巖； (d)安山巖

3 滲透率的定量計算方法

基于核磁共振T2模型，常規砂巖儲層滲透率的計算公式為[30]

K=aT2gm2φ4

(5)

式中：a為經驗常數；T2gm是橫向弛豫時間T2分布的幾何平均值。

在復雜儲層中，復雜的孔隙結構導致φc與φ存在較大差異，而對滲透率起主要貢獻的是φc。因此，本文將復雜儲層滲透率的計算公式修改為

(6)

式中：Kcomp為復雜儲層的滲透率；T2gm-comp是復雜儲層橫向弛豫時間T2分布的幾何平均值。

φc與φ呈乘冪(φc=bφd)、指數(φc=bedφ)、線性(φc=bφ+d)和多項式(φc=b1φ3+b2φ2+b3φ+d)四種典型函數關系，相應四種復雜儲層滲透率的計算公式分別為

(7)

(8)

(9)

(10)

式中b、b1、b2、b3、d均為系數。

基于式(7)～式(10)，復雜儲層滲透率的計算公式表達為

(11)

式中c為系數。

進一步簡化式(11)，可以得到

(12)

式中x為儲層的孔隙度指數。如果計算砂巖的滲透率，則x取為4。而石灰巖儲層滲透率的計算公式為

(13)

式中：Klime為石灰巖儲層的滲透率；T2gm-lime是石灰巖儲層T2分布的幾何平均值。

石灰巖儲層具強非均質性，即使在相近的孔隙度條件下，石灰巖儲層的滲透率與常規砂巖儲層的滲透率也會存在較大差異。因此，假定相近孔隙度條件下，石灰巖與常規砂巖的儲層滲透率的比值

(14)

式中：Ksand為砂巖儲層的滲透率；T2gm-sand是砂巖儲層T2分布的幾何平均值。

由式(14)可以得到石灰巖儲層孔隙度指數

(15)

在相近孔隙度條件(孔隙度小于20%)下，當T2gm-lime=T2gm-sand，y小于1時，φ、x、y之間的關系如圖7所示。由圖可知，x的分布范圍為4.0～8.3；φ逐漸變大，x逐漸變大；y逐漸變小，x逐漸變大。

在相近孔隙度條件(孔隙度小于20%)下，當T2gm-lime明顯大于T2gm-sand，即T2gm-lime≠T2gm-sand時，φ、x、y之間的關系如圖8所示，可見x的分布范圍為5.9～13.7。

聯立式(13)和式(15)可以得到石灰巖儲層滲透率的計算公式

(16)

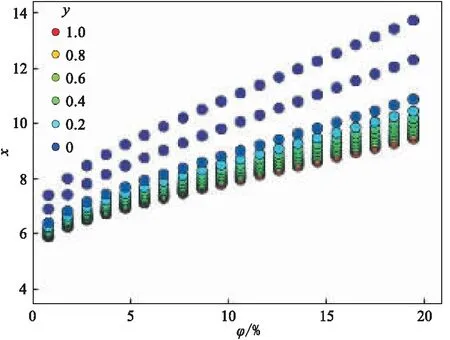
圖8 T2不同時，φ、x與y之間的關系

4 應用效果

選用A井部分層段石灰巖儲層(圖9)測試本文方法應用效果。

由圖9可見，基于測井曲線所計算的孔隙度(φLog)與巖心分析的孔隙度(φCore)之間的吻合程度較高； 基于核磁共振T2模型所計算的滲透率(KSDR)與巖心分析的滲透率(KCore)之間誤差相對較大，平均絕對誤差為20.41mD； 基于核磁共振自由流體模型所計算的滲透率(KCoates)與KCore之間誤差相對較大，平均絕對誤差為21.75mD； 基于核磁共振測井、采用式(16)所計算的滲透率(Klime)與KCore之間誤差相對較小，平均絕對誤差為0.83mD。因此，基于連通孔隙度的滲透率定量計算方法可以提高石灰巖儲層滲透率預測的精度。

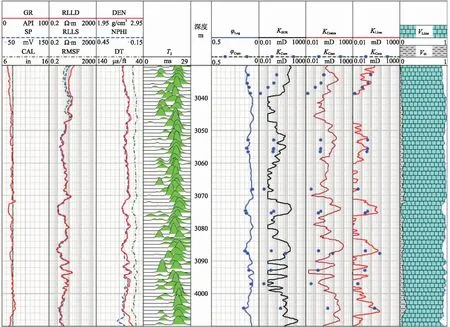
圖9 A井部分層段石灰巖儲層滲透率處理成果

5 結論

本文研究了復雜儲層連通孔隙度評價與滲透率定量計算方法，并建立了連通孔隙度模型、孔隙度指數模型及普適性的核磁共振T2模型。主要結論如下。

(1)核磁共振實驗可以定量計算連通孔隙度，但不能直觀顯示不同類型孔隙之間的連通性； CT掃描成像不僅可以在空間上直觀顯示不同類型孔隙之間的連通性，也可以定量計算連通孔隙度。

(2)由于導電孔隙度與連通孔隙度所表征的孔隙空間相同，因此以導電孔隙度為橋梁，建立了連通孔隙度的計算模型，明確了不同類型巖石中連通孔隙度與總孔隙度的函數關系。二者的函數形式不盡相同，主要表現為線性、多項式、乘冪和指數等。這揭示了總孔隙度相近、連通孔隙度不同是導致滲透率存在較大差異的根本原因。

(3)采用連通孔隙度的計算模型改進了核磁共振T2模型，形成了復雜儲層滲透率的定量計算方法，大幅度地提高了石灰巖儲層滲透率的計算精度。