板塊運動模型對跟蹤站坐標時序解算影響分析

曹多明，成英燕，常春濤，盧 浩，王周杰

板塊運動模型對跟蹤站坐標時序解算影響分析

曹多明1,2,3，成英燕1,3，常春濤1,3，盧 浩1,2,3，王周杰1,2,3

（1. 中國測繪科學研究院，北京 100036；2. 山東科技大學測繪與空間信息學院, 山東 青島 266590；3. 北京房山人衛激光國家野外科學觀測研究站，北京 102488）

針對目前常用站點坐標時序來反演板塊運動趨勢，卻很少意識到板塊運動也是引起站點坐標變化主要因素的問題，提出一種利用板塊運動模型改正測站坐標時序解算精度的思路。以斯克里普斯軌道和永久陣列中心（SOPAC）網站提供的2017—2019年共3 a的全球單日松弛解H文件作為原始數據，選擇北美（NOAM）、歐亞（EURA）、澳大利亞（AUST）、南美（SOAM）4個板塊為研究區域。實驗結果表明，顧及站點距離板塊邊界的有效距離，施加板塊運動模型后，能有效提升站點水平方向坐標時間序列的精度，各板塊內平均精度提升率都能達到60%以上，同時驗證了模型在站點水平速度場解算中的可用性。

板塊運動；板塊運動模型；坐標時間序列；板塊邊界；速度場

0 引言

衛星跟蹤站的坐標時間序列是指站點單日解算出的坐標在時間域上進行的排列，精確可靠的坐標時間序列是研究地球動力學的數據基礎[1-2]。因此，目前眾多學者的研究更多是偏向于用站點坐標時序來反演板塊運動模型，但是受制于地球板塊運動及地表各種負荷的影響，地球表面的衛星跟蹤站在國際地球參考框架（international terrestrial reference frame, ITRF）下的位置處在不斷變化中[3-5]，此時顧及板塊運動趨勢對站點時序解算的影響變得尤為重要。

板塊運動是指巖石圈與地心的相對運動[6]，附在地球板塊上的站點隨板塊的運動滿足歐拉定義，反映的是水平方向的運動趨勢[7-8]，并且板塊運動模型的建立，需要借助數百萬年的地球物理觀測數據或者近幾十年的空間大地測量觀測資料[9]。現階段對站點坐標時序分析以及板塊運動模型建立研究成果頗多[10]。文獻[11]研究提出施加噪聲模型，能有效提升序列的精度；文獻[12]研究表明，施加基于小波分解的奇異譜分析也可以提升序列精度；文獻[13]利用ITRF2005框架下的站點數據研究，建立了國際地球參考框架2005板塊速度場（ITRF 2005 velocity, ITRF2005-VEL）模型；而文獻[14]顧及板塊劃分研究，利用ITRF2008框架下的站點數據提出了相對巖石圈無整體旋轉56個板塊速度場（no net rotation mid-ocean ridge velocity 56, NNR-MOR-VEL56）模型。

上述研究主要是針對如何提升站點坐標時序精度給出的常規策略，以及有效建立板塊運動模型的一般方法，且對板塊運動模型的應用也局限于參考框架的動態維持和坐標轉化等，卻少有嘗試將板塊運動模型應用到站點坐標時序解算的改正中。本文基于文獻[15]建立的ITRF2014框架下的板塊運動模型（ITRF 2014 plate motion model, ITRF2014-PMM），首先分析模型對站點坐標時序解算的改正情況，其次評價模型在各板塊內對坐標時序達到最佳使用的匹配性，并驗證模型在站點速度場解算中的可用性。

1 ITRF2014-PMM板塊運動模型理論與算法

1.1 板塊運動模型簡介

ITRF2014-PMM是文獻[15]在2016年基于ITRF2014框架給出的站點坐標和速度值研究基礎上建立的，與ITRF2014框架具有最大的一致性。模型參考了板塊邊界2002模型（plate boundaries model 2002, PB2002）給出的板塊劃分，選取其中11個板塊進行了參數求解。在選擇建模站點時，文獻[15]對ITRF2014框架下的國際全球衛星導航系統服務（international global navigation satellite system service, IGS）站點進行嚴格篩選，既要滿足剛性板塊運動假說，又要滿足遠離板塊邊界、變形帶區域以及冰川均衡調整區域（glacial isostatic adjustment, GIA），并以100 km作為距離邊界的限值，最終有297個站點符合要求。

1.2 板塊運動建模方法

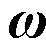
當從整體角度估計多個板塊旋轉極點時，可以引入一個中心偏移運動分量，則式（1）改寫為

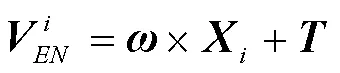
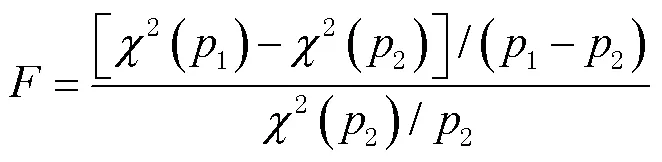
綜合以上分析，文獻[15]在建立模型時選擇對ORB不進行估計，同樣滿足大地測量的應用要求。因此使用式（1）作為模型的基礎計算公式，因板塊運動在水平方向反映效果明顯，所以只對該測站在水平方向進行展開，即

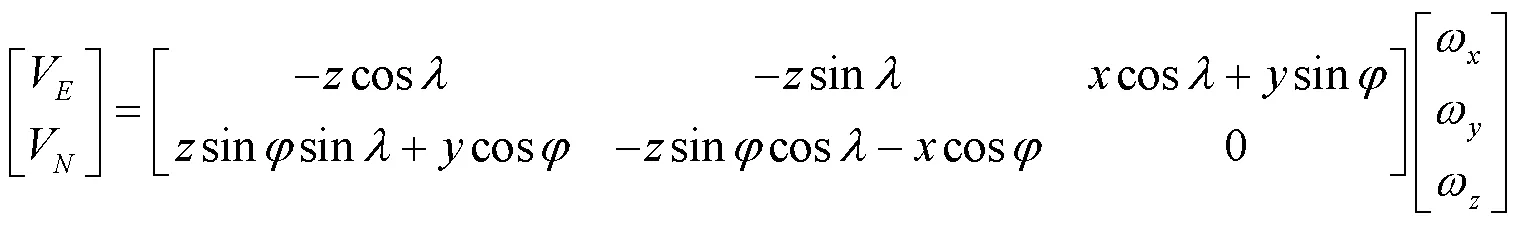
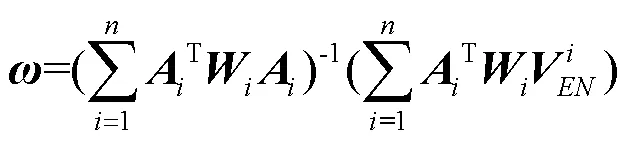
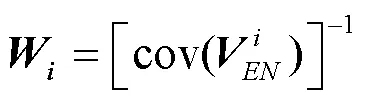
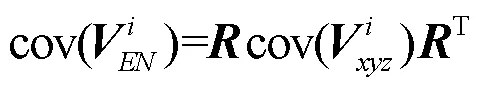
式中，為從地心坐標系到站心地平坐標系的旋轉矩陣。的計算公式為

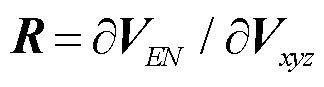
在建立的ITRF2014-PMM過程中，同時對所有板塊進行擬合[17]，得到11個板塊的旋轉極點，模型的平均精度能達到0.3 mm/a，最終求解的參數如表1所示。

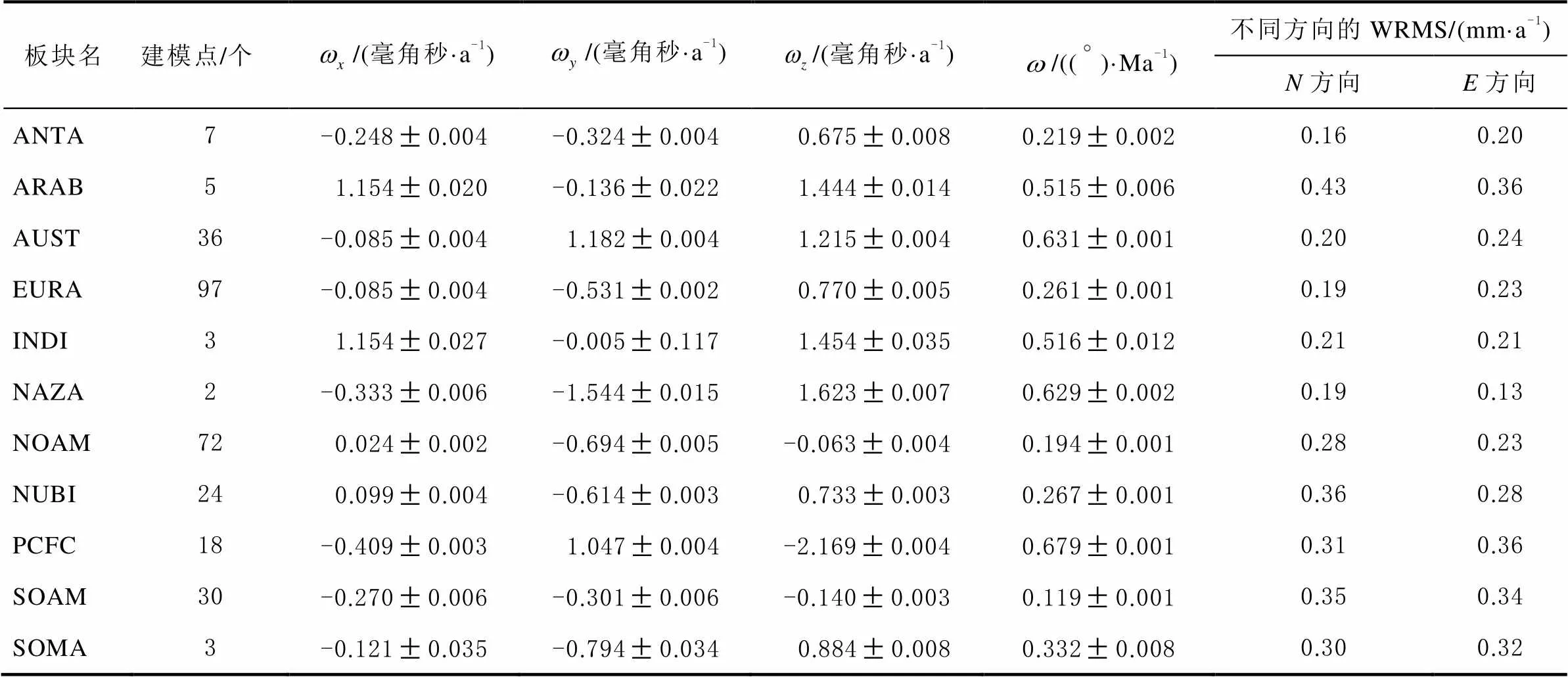
表1 ITRF2014-PMM模型參數

注：ARAB為阿拉伯半島板塊（Arabia）；AUST為澳大利亞板塊（Australia）；EURA為歐亞板塊（Eurasia）；INDI為印第安板塊（India）；NAZA為納斯卡板塊（Nazca）；NOAM為北美板塊（North America）；NUBI為努比亞板塊（Nubia）；PCFC為太平洋板塊（Pacific）； SOMA為索馬里板塊（Somalia）； SOAM為南美板塊（South America）；ANTN為南極洲板塊（Antarctic）；WRMS為加權均方根誤差（weighted root mean squared）。

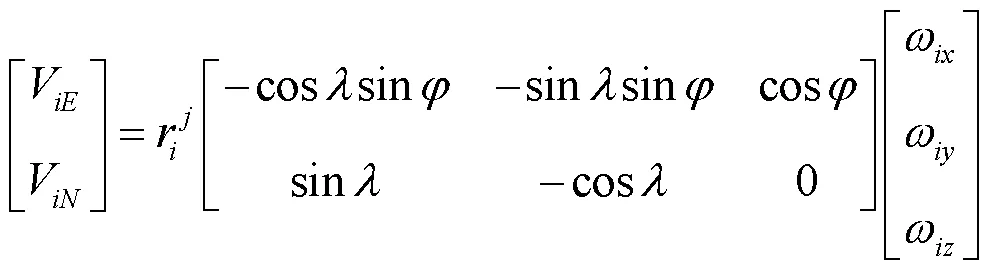
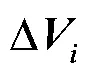
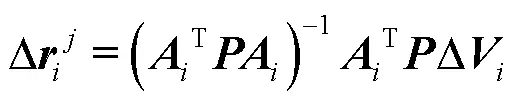
式中，為單位權矩陣。

2 衛星跟蹤站數據解算

2.1 實驗數據準備

為確保實驗數據處理的可說服性，本文選擇對斯克里普斯軌道和永久陣列中心（scripps orbit and permanent array center, SOPAC）網站提供的2017—2019年共3 a的全球單日松弛解H文件進行處理，數據時間跨度處于板塊運動模型采用的建模點歷元之后，期間同時借助了全局卡爾曼濾波器（global Kalman filter, GLOBK）數據處理軟件，完成H文件平差解算，軟件版本為5.32。

1）解算控制點選取。在進行全球單日松弛解H文件平差之前，需要在全球范圍內選擇IGS控制站點，可以按照以下步驟進行[18]：①收集整理全球框架下臺站的觀測資料，參考目前通用標準，兼顧站點數據的連續性、穩定性、平衡性、高精度、多種解以及精度一致等原則，完成控制站點的初選；②采用7參數法進一步對控制站點進行精選；③在上一步的基礎上，繼續利用監督分類法完成站點均勻分布處理。最終選擇出全球分布的92個框架點作為控制點，如圖1所示。

圖1 控制點分布圖【審圖號：國審字（2022）第00987號】

2）剔除殘差超限點。先對全球單日松弛解H文件不施加模型進行正常解算，然后統計北美（NOAM）、歐亞（EURA）、澳大利亞（AUST）、南美（SOAM）4個板塊上IGS站點的坐標值，將解算得到的站點坐標與ITRF官網給出的坐標值作差，剔除坐標殘差絕對值大于2倍標準差（）的站點[9]，最終選出228個站點參與后繼模型改正實驗。各板塊上站點分布如圖2所示，最終剩余的站點數如表2所示。

表2 各板塊最終剩余站點數

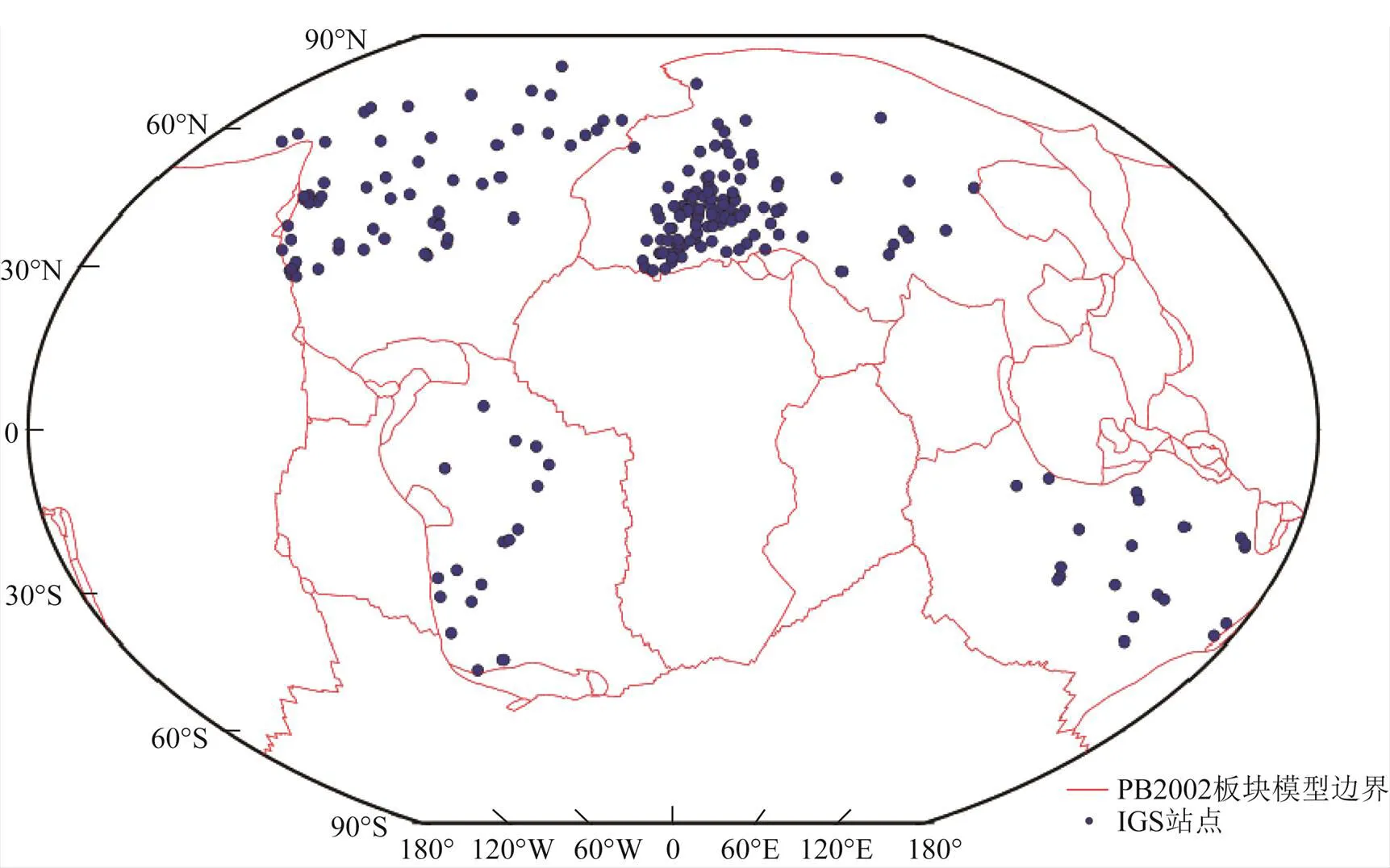
圖2 4個板塊上所選站點分布圖【審圖號：國審字（2022）第00987號】

2.2 數據處理方案

本文在解算過程中先對4個板塊不施加模型改正，然后再分別對各板塊施加對應模型改正。實驗將按圖3所示的流程進行分析。

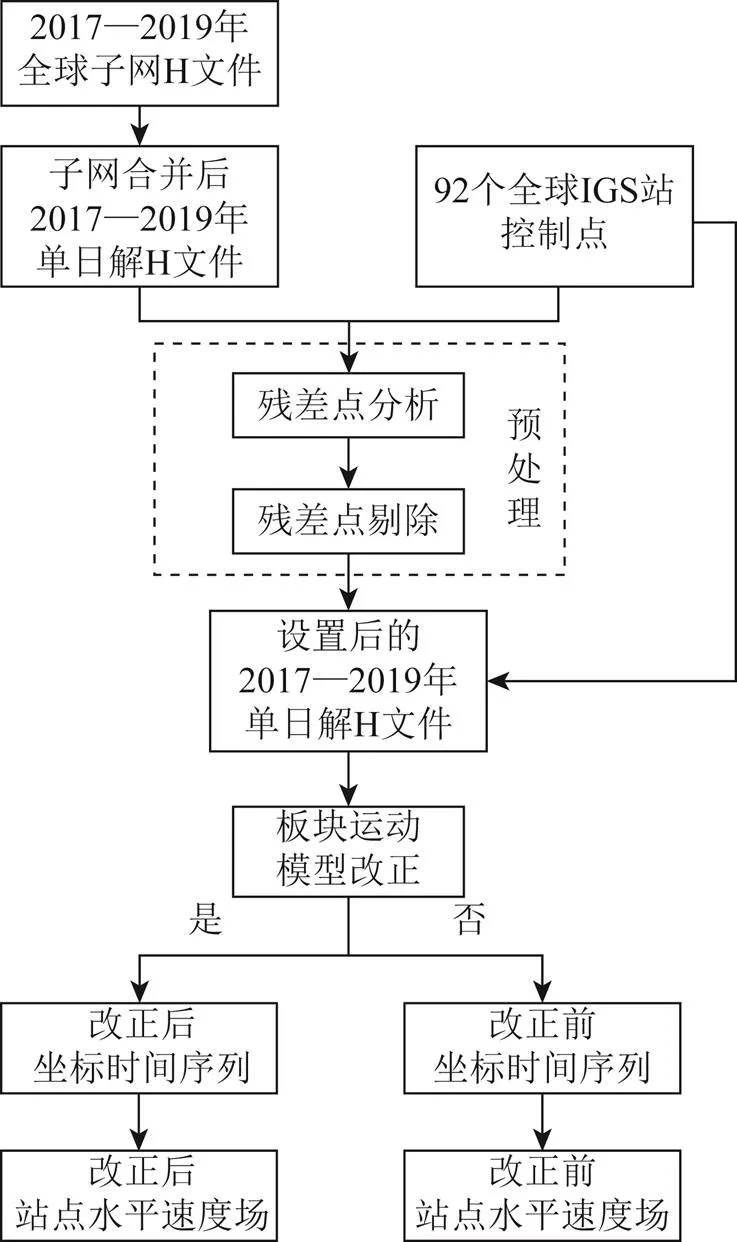
圖3 實驗數據處理流程

2.3 解算結果分析

本文首先對各板塊內站點的坐標時間序列精度改正情況進行了分析，然后驗證了施加板塊運動模型對站點速度解算的可用性。

1）坐標時序解算精度。對站點坐標時間序列精度的描述，一般采用標準化均方根誤差（normalized root mean square, NRMS）和加權均方根誤差（weighted root mean squared, WRMS）。兩種誤差值都可反映站點坐標時間序列的不確定度，其值越小，反映的精度越高[19-20]。鑒于此，本文選擇WRMS值來反映解算的站點坐標時序精度情況，其計算公式為

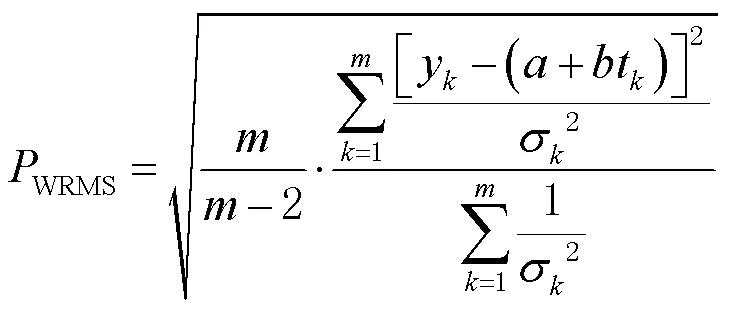
統計各板塊上各站點在施加板塊運動模型改正前后，其坐標時間序列對應的WRMS值，如圖4至圖7所示。

由圖4至圖7知，在水平方向上，各板塊內站點在施加板塊運動模型后坐標時間序列的精度均得到有效提升。其中EURA、AUST、SOAM三個板塊站點坐標時間序列改正效果明顯，而NOAM板塊出現了個別站點坐標時間序列改正異常現象，異常的原因將在后面具體探討。

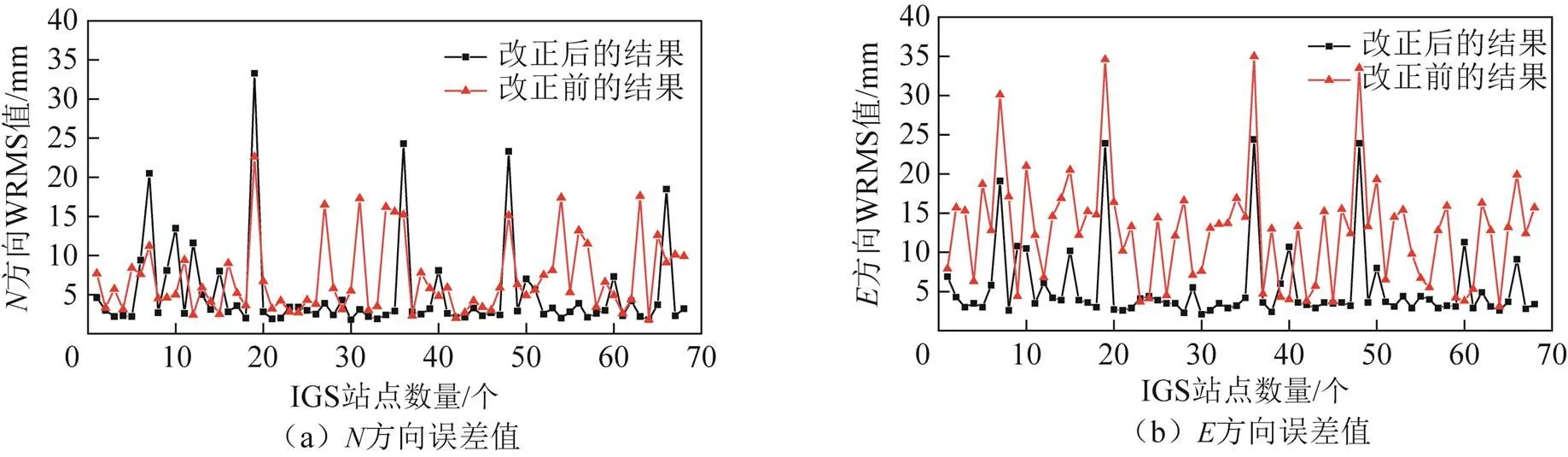
圖4 NOAM板塊模型改正前后站點坐標時間序列WRMS值

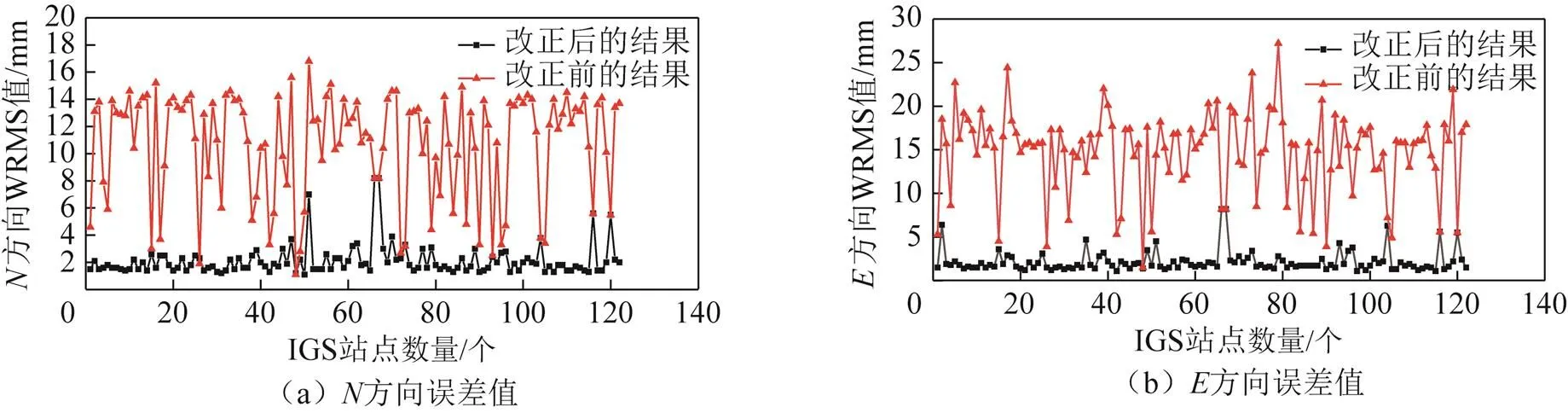
圖5 EURA板塊模型改正前后站點坐標時間序列WRMS值

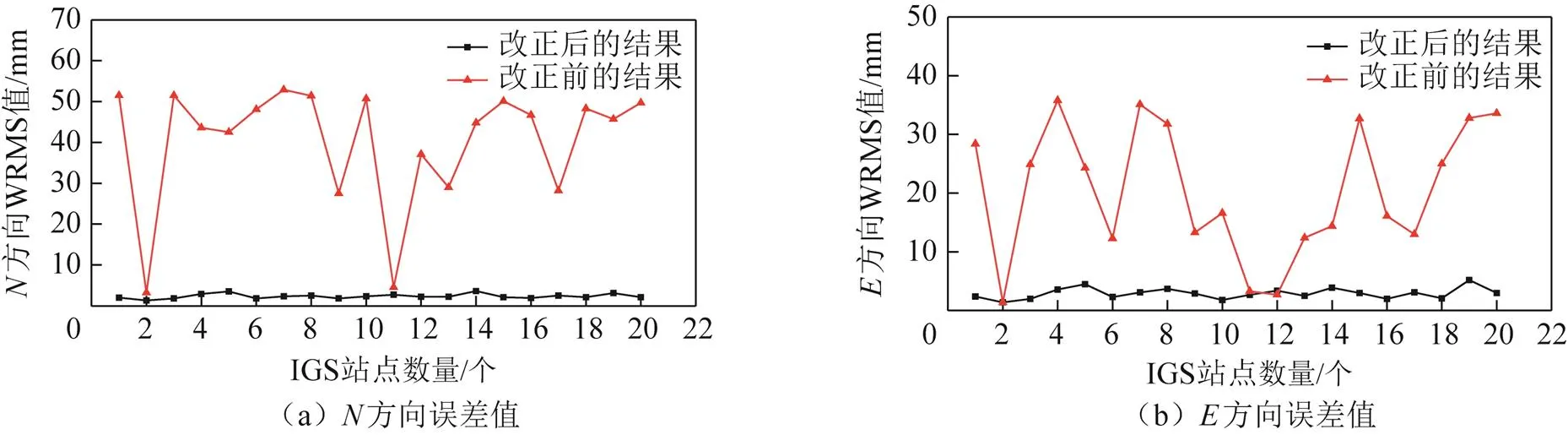
圖6 AUST板塊模型改正前后站點坐標時間序列WRMS值

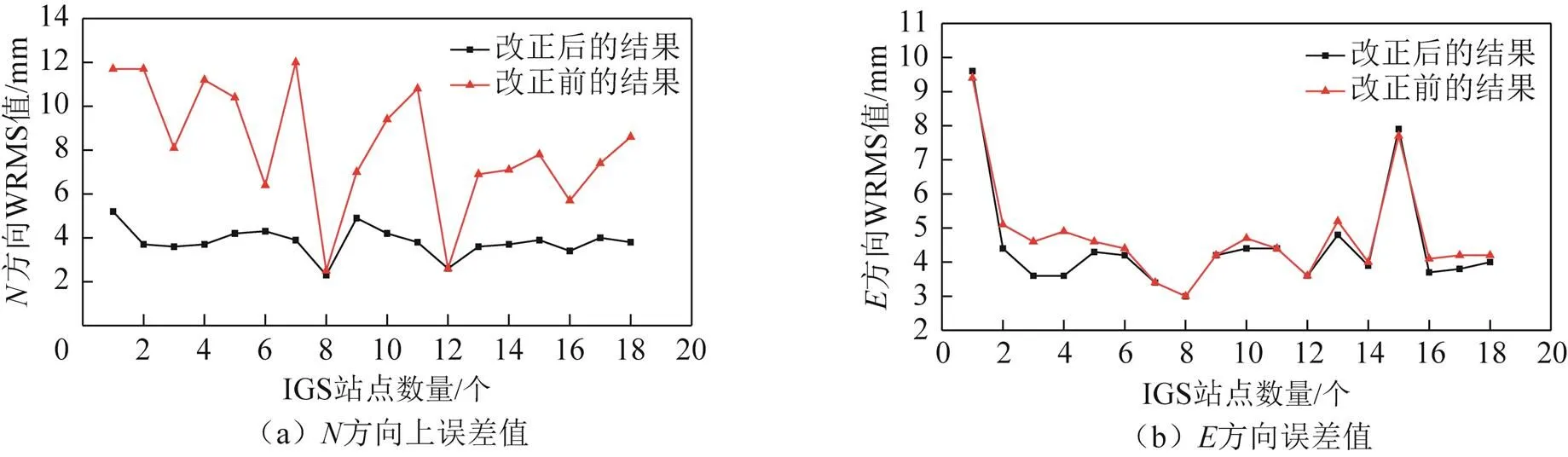
圖7 SOAM板塊模型改正前后站點坐標時間序列WRMS值

不考慮出現改正異常現象的站點，將各板塊在模型改正前后得到的站點坐標時序精度作差，差值大小反映了坐標時序精度的提升量，表3統計了板塊模型改正前后站點坐標時間序列WRMS差值的最大值、最小值以及平均值三項指標。

由表3可知，AUST板塊內站點坐標時間序列精度的提升量最大，說明模型在此板塊內對站點坐標時間序列的改正代表性最強，改正效果最為明顯；SOAM板塊內站點坐標時間序列精度的提升量最小，說明模型在此板塊內本身精度相對較低，因此對站點序列的改正效果略差；而EURA和AUST板塊內站點坐標時序精度的提升量相當。出現上述各板塊內站點坐標時序精度提升情況各異的原因，可能跟文獻[15]建立板塊運動模型時所選用的建模點數量不等有關，導致建立的模型本身精度在各板塊上存在差異，此外也與各板塊本身的運動活躍程度有關。

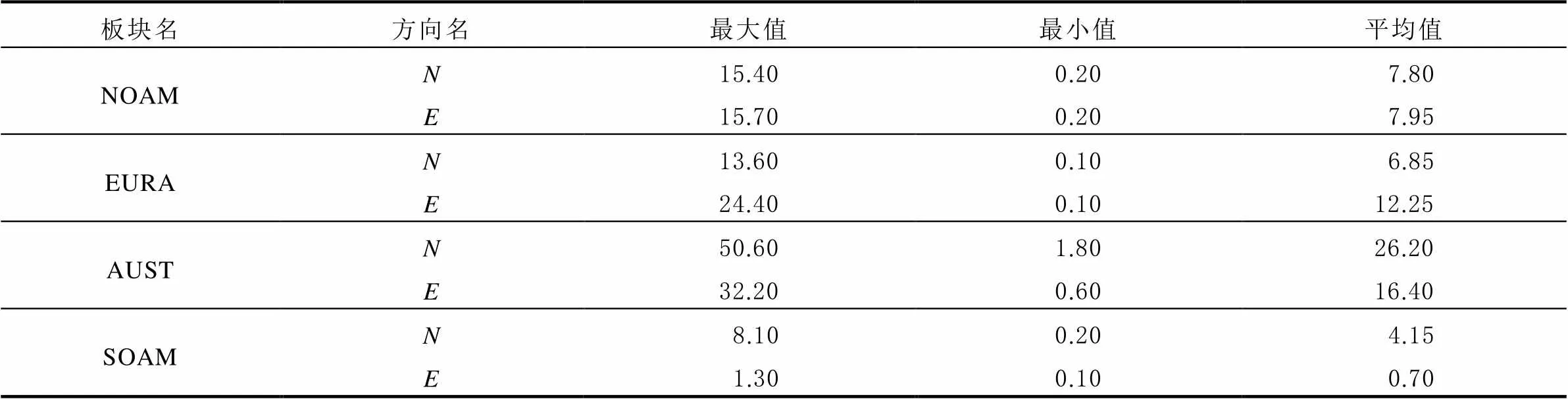
表3 各板塊模型改正前后站點坐標時間序列WRMS 的差值統計 單位：mm

2）坐標時序解算精度提升率。在施加模型改正后，統計各板塊內坐標時間序列精度保持不變以及精度降低的站點，將其統稱為異常點，計算各板塊內站點坐標時間序列精度的提升率，如表4所示。

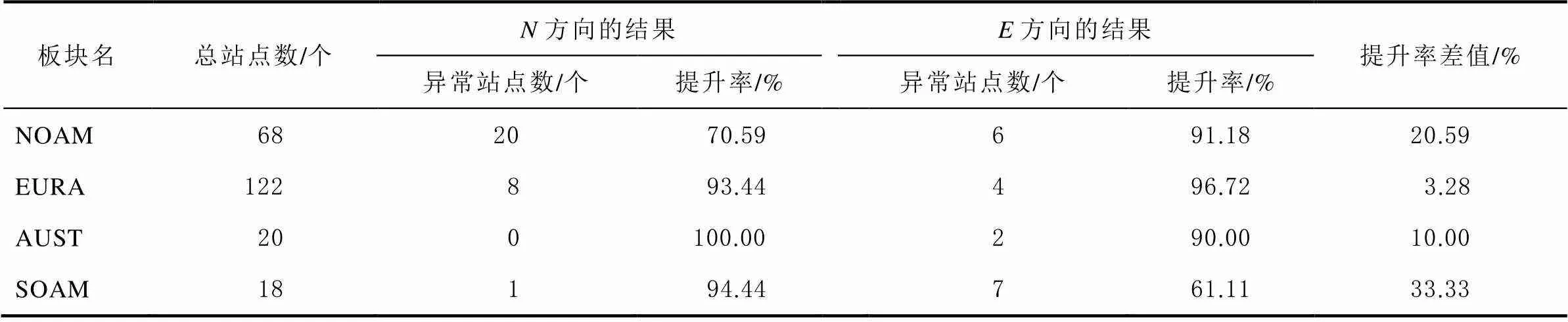
表4 各板塊站點坐標時間序列精度提升率

注：提升率差值指的是同一測站上方向與方向上精度提升率作差得到的絕對值。

由表4知，NOAM板塊的異常站點個數最多，其次是EURA、SOAM以及AUST板塊。各板塊在施加模型改正后站點坐標時間序列精度的平均提升率都能達到60%以上，其中EURA板塊在方向的精度平均提升率達到96.72%，AUST板塊在方向的精度平均提升率達到100%；并且EURA板塊在、方向上精度提升率差值最小，說明模型對其水平兩方向的改正較為一致，而SOAM板塊在、方向上的精度提升率差值最大，說明模型對其水平兩方向的改正存在差異。

3）坐標時序改正有效距離。為探究各板塊上異常點出現的原因，統計各板塊內站點坐標時間序列精度的提升情況，根據站點位置繪制到PB2002全球板塊模型分布圖上，如圖8所示。

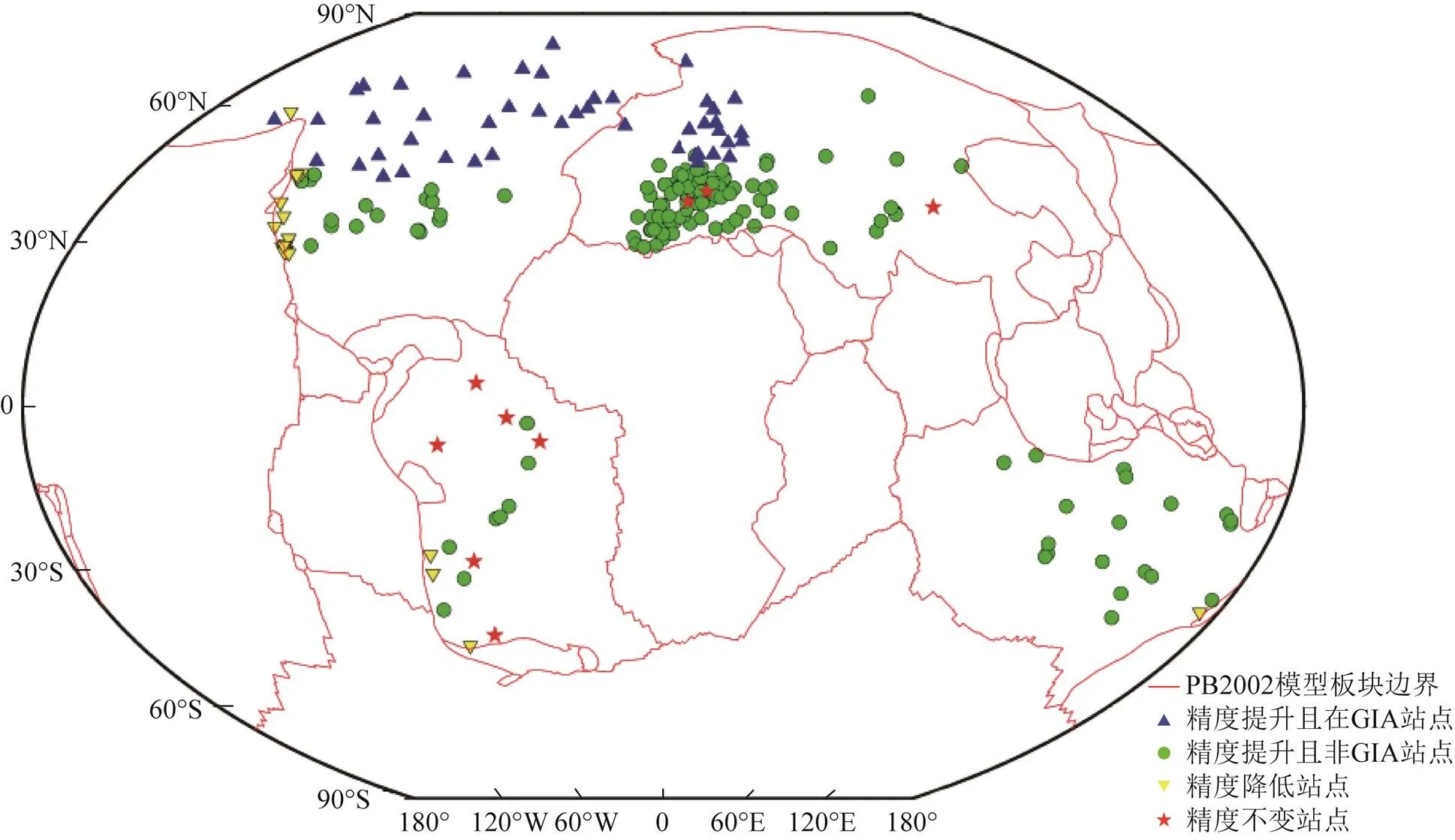
圖8 各板塊站點解算情況分布【審圖號：國審字（2022）第00987號】

由圖8可知，施加模型改正后坐標時間序列精度降低的站點主要分布于板塊邊界區域，以NOAM板塊北部最為顯著，造成的原因可能與這些區域地質運動過于活躍有關；施加模型改正后坐標時間序列精度不變的站點主要位于板塊中間區域，以SOAM、EURA板塊最為顯著，造成的原因可能與這些區域地質運動較為穩定，或者個別站點十分靠近建模站點等因素有關；文獻[15]建立板塊運動模型時所選擇的建模點全都遠離GIA區域，而位于GIA區域的站點在施加模型改正后坐標時間序列精度仍得到有效提升，以NOAM、EURA板塊北部區域最為顯著，說明模型對GIA區域站點坐標時間序列的改正同樣適用。

顧及施加模型改正后坐標時間序列精度降低的站點主要位于板塊邊界，為更好地探究板塊運動模型對板塊內站點坐標時間序列解算精度發揮改正作用的有效性，計算了各板塊內站點距離板塊邊界的有效距離，其值應為精度降低站點距邊界最大距離與精度提升站點距邊界最小距離的差值，如表5所示。

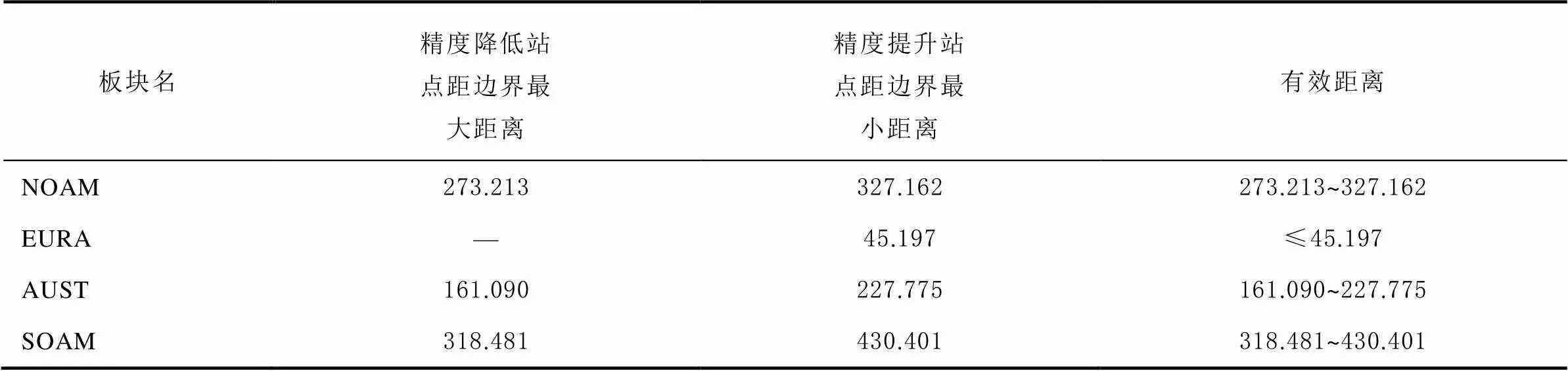
表5 各板塊站點坐標時間序列改正有效距離統計 單位：km

由表5對比可知，EURA板塊發揮改正的有效距離最短，處于45.197 km以下；而SOAM板塊發揮改正的有效距離最大，處于318.481～430.401 km之間。

4）板塊內站點速度解算。為驗證板塊運動模型在各板塊內對站點速度值解算的實用性，將各板塊施加模型前后解算出的站點速度與ITRF官網公布的站點速度值分別求差，計算各板塊內站點速度的標準差，如圖9所示。

由于國際地球自轉服務組織公布的ITRF2014速度信息是基于地心坐標系，而一般選擇在水平方向上對站點運動速度進行描述，因此需要先對速度進行轉換[12]，即

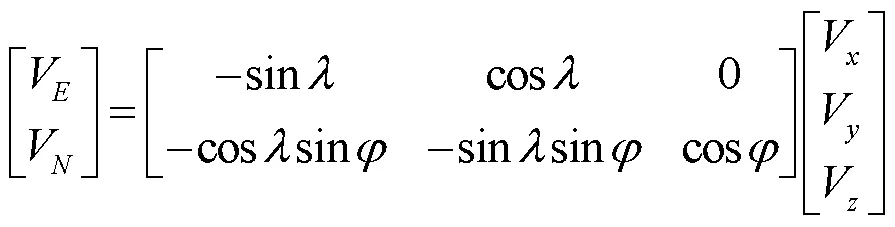
由圖9可知，在水平方向上，各板塊在施加模型后計算出的站點速度標準差均小于未施加模型的站點速度標準差，說明施加板塊運動模型能有效改正站點的水平速度值，驗證了模型在站點速度求解中的可用性。

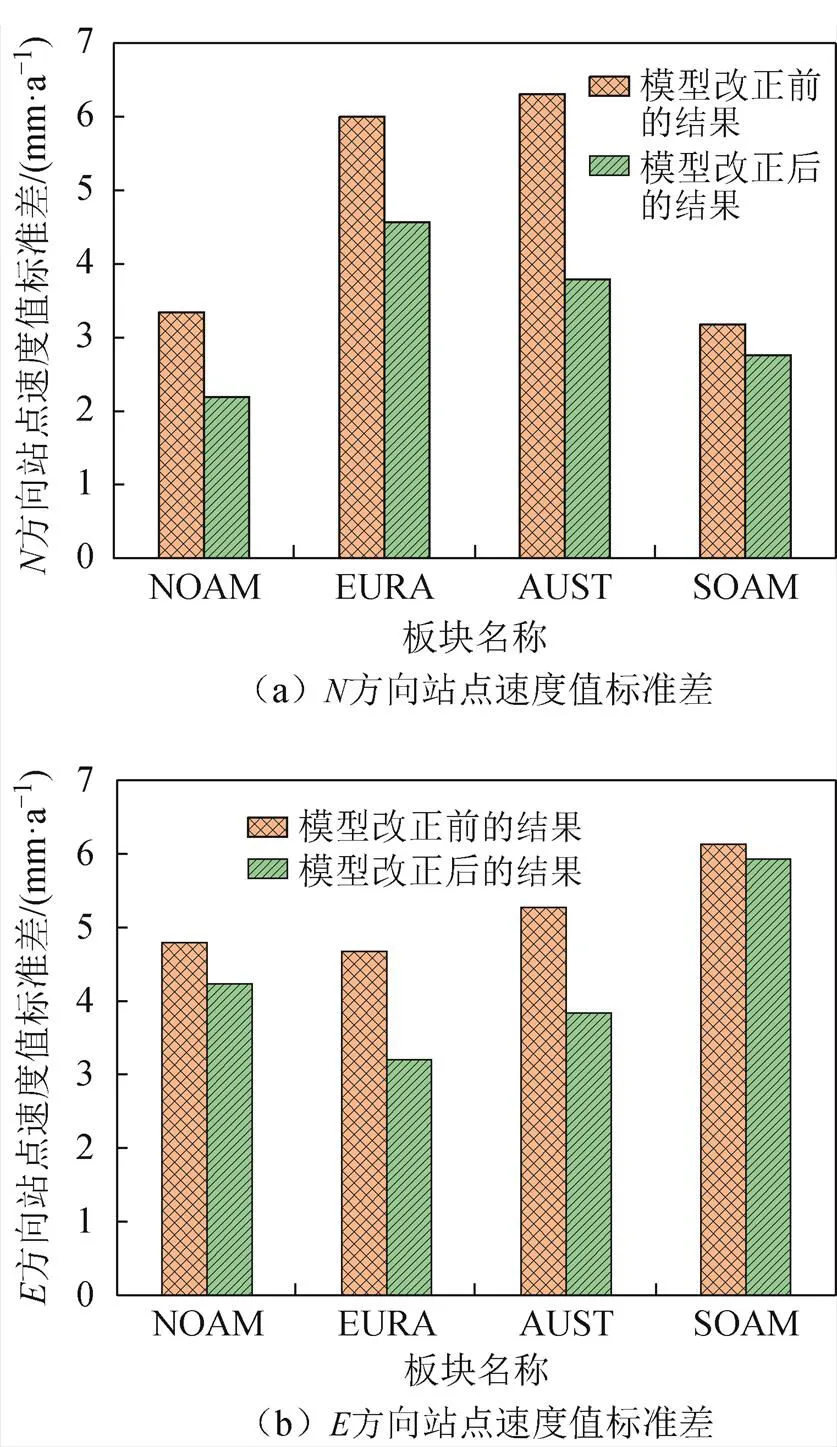
圖9 各板塊模型改正前后站點速度值標準差

3 結束語

現階段眾多學者常用站點坐標時序來反演板塊運動趨勢，卻忽視了板塊運動也是引起站點坐標變化的主要因素。本文首先對ITRF2014-PMM板塊運動模型進行了詳細介紹，然后以SOPAC網站產出的2017—2019年共3 a的全球單日松弛解H文件作為原始數據，選擇對NOAM、EURA、AUST、SOAM四個板塊分別施加對應的ITRF2014-PMM改正模型，以研究模型對站點坐標時間序列解算精度的影響情況，并探究了模型在站點速度解算中的實用性，得出以下結論：

1）施加ITRF2014-PMM改正模型能有效提升站點水平坐標時間序列解算精度，4個板塊內精度提升率都能達到60%以上，其中EURA板塊在方向的精度提升率能達到96.72%，而AUST板塊在方向的精度提升率能達到100%。

2）ITRF2014-PMM改正模型在各板塊上本身的建模精度存在差異，因此對各板塊內站點坐標時間序列的改正效果各不相同。AUST板塊內站點的坐標時間序列精度提升量最大，說明模型在此板塊內對站點坐標時間序列的改正代表性最強，改正效果最為明顯；而SOAM板塊內站點的坐標時間序列精度提升量最小，說明模型在此板塊內本身精度相對較低，因此對站點序列的改正效果略差。

3）ITRF2014-PMM改正模型對處在板塊邊界上站點的坐標時間序列改正仍效果不佳，但對位于GIA區域內站點的坐標時間序列改正卻同樣適用；模型在各板塊上對站點坐標時間序列改正的有效距離也各不相同，其中在EURA板塊上的有效距離最短，而在SOAM板塊上的有效距離最大。

4）分析實驗數據驗證了ITRF2014-PMM改正模型在速度場解算中的可用性，施加模型能有效改善站點水平方向的速度值精度。

綜上所述，現階段利用衛星跟蹤站長期觀測數據進行坐標時間序列解算時，顧及站點距離板塊邊界的有效距離，施加ITRF2014-PMM改正模型能有效提升站點坐標時間序列解算的精度，可為各板塊內水平速度場解算等提供參考。因為本文采用全球子網數據進行數據處理，經數據預處理后，某些板塊內剩余可分析的站點數減少，所以后繼還需借助各板塊內更多連續運行參考站（continuously operating reference stations, CORS）長期觀測數據進行解算驗證，增強實驗結果的說服性。

[1] 賀小星, 花向紅, 周世健, 等. PCA與KLE相結合的區域GPS網坐標序列分析[J]. 測繪科學, 2014, 39(7): 113-117, 97.

[2] 舒穎, 賀小星, 花向紅, 等. GPS單日解序列解算策略性能分析[J]. 測繪科學, 2018, 43(6): 7-12.

[3] 高樂, 成英燕, 廖靜娟. CGCS2000板塊運動模型建立方法研究[J]. 大地測量與地球動力學, 2011, 31(6): 58-62.

[4] 張西光, 呂志平. 論地球參考框架的維持[J]. 測繪通報, 2009(5): 1-4.

[5] 姜衛平, 馬一方, 鄧連生, 等. 毫米級地球參考框架的建立方法與展望[J]. 測繪地理信息, 2016, 41(4): 1-6, 12.

[6] 張瓊, 王世民, 趙永紅, 等. 采用剪切波分裂方向約束的板塊絕對運動模型研究[J]. 地球物理學報, 2020, 63(1): 172-183.

[7] 呂志鵬. 板塊運動幾何模型的比較[J]. 測繪通報, 2015(12): 15-19.

[8] 王敏, 岳彩亞, 王曉峰, 等. 二級板塊分布的GPS臺站非線性運動研究[J]. 測繪科學, 2018, 43(11): 165-170.

[9] 程鵬飛, 成英燕, 秘金鐘, 等. CGCS2000板塊模型構建[J]. 測繪學報, 2013, 42(2): 159-167.

[10] 金波文, 王慧, 劉玉龍, 等. 中國沿海海洋站GNSS坐標時間序列噪聲模型的建立與分析[J]. 大地測量與地球動力學, 2020, 40(5): 476-481.

[11] 戴海亮, 孫付平, 姜衛平, 等. 小波多尺度分解和奇異譜分析在GNSS站坐標時間序列分析中的應用[J]. 武漢大學學報(信息科學版), 2021, 46(3): 371-380.

[12] 朱新慧, 孫付平, 王刃. 基于ITRF2005的全球板塊運動模型[J]. 地球物理學進展, 2009, 24(3): 859-865.

[13] 柴洪洲, 明鋒, 段婷婷, 等. 全球板塊運動背景場及ITRF2005VEL的建立[J]. 測繪科學技術學報, 2009, 26(2): 79-81.

[14] 李亞萍, 孫付平, 門葆紅, 等. 基于ITRF2008的NNR-MORVEL56的全球板塊運動參數求解[J]. 全球定位系統, 2016, 41(2): 14-19.

[15] ALTAMIMI Z,MéTIVIER L,REBISCHUNG P,et al.ITRF2014 plate motion model[J].Geophysical Journal International, 2017, 209(3): 1906-1912.

[16] 李春曉. 利用ITRF2008分析全球板塊運動[J]. 大地測量與地球動力學, 2015, 35(5): 829-834.

[17] 朱新慧, 孫付平, 秦勇. 組合GPS和VLBI數據建立板塊運動模型[J]. 武漢大學學報(信息科學版), 2005, 30(7): 604-608.

[18] 程鵬飛, 成英燕. 基于GNSS的CGCS2000數據處理技術綜述[J]. 武漢大學學報(信息科學版), 2018, 43(12): 2071-2078.

[19] 龔國棟, 賀小星, 花向紅, 等. GPS網共模誤差的空間響應分析[J]. 大地測量與地球動力學, 2016, 36(11): 951-957.

[20] 姜衛平, 李昭, 鄧連生, 等. 高階電離層延遲對GPS坐標時間序列的影響分析[J]. 科學通報, 2014, 59(10): 913-923.

Analysis of influence of plate motion model on coordinate time series calculation of tracking station

CAO Duoming1,2,3, CHENG Yingyan1,3, CHANG Chuntao1,3, LU Hao1,2,3, WANG Zhoujie1,2,3

(1. Chinese Academy of Surveying and Mapping, Beijing 100036, China; 2. College of Geodesy and Geomatics, Shandong University of Science and Technology, Qingdao, Shandong 266590, China; 3. BeijingFangshanSatelliteLaserRangingNationalObservationandResearchStation,Beijing 102488,China)

In view of the fact that the station coordinate time series are commonly used to invert the trend of plate motion, it is seldom realized that the plate motion is also the main factor causing the station coordinate change, this paper proposes an idea of using the plate motion model to correct the accuracy of the station coordinate time series. The global one-day relaxation solution H file of three years from 2017 to 2019 produced by Scripps Orbit and Permanent Array Center (SOPAC) website is taken as the original data, the North American (NOAM), Eurasian (EURA), Australian (AUST) and South American (SOAM) plates are selected as the research areas. The experimental results show that, applying the plate motion model can effectively improve the accuracy of the station horizontal coordinate time series, and the average accuracy improvement rate of each plate can reach more than 60%, at the same time, the availability of the model in the station horizontal velocity field calculation is verified.

plate motion; plate motion model; coordinate time series; plate boundary; velocity field

P228

A

2095-4999(2022)02-0044-09

曹多明, 成英燕, 常春濤, 等. 板塊運動模型對跟蹤站坐標時序解算影響分析[J]. 導航定位學報, 2022, 10(2): 44-52.（CAO Duoming, CHENG Yingyan, CHANG Chuntao, et al. Analysis of influence of plate motion model on coordinate time series calculation of tracking station[J]. Journal of Navigation and Positioning, 2022, 10(2): 44-52.）

10.16547/j.cnki.10-1096.20220206.

2021-05-21

國家重點研發計劃項目（2016YFB0501405）。

曹多明（1996—），男，安徽馬鞍山人，碩士研究生，研究方向為參考框架維持與GNSS測量數據處理。

成英燕（1964—），女，山西臨汾人，博士，研究員，研究方向為大地測量基準與GNSS測量數據處理。