將方程思想熔鑄到天平模型中

江蘇無錫市峰影小學（214000） 王金鋒

方程的教學重點是指導學生深入理解并牢固掌握等式的結構，領悟含有未知數的等式是方程的深刻含義；教學難點是引導學生搭建方程的基本模型，滲透設未知數列方程解應用題的解題思想。同時，本課教學還擔負著培養學生觀察、對比、思索與解析等各方面的能力，以及訓練學生思維的靈敏度和思路的變通性的重要任務。

一、回顧，感知平衡

師：大家還能記起游樂園里的場景嗎？老師收集了一些兒童樂園的照片，一起來回顧吧！（PPT 展示：各種娛樂器材上孩童玩耍的身影）

師：照片中哪類游戲人氣最高？

生1：玩蹺蹺板的人最多。有兩人組，有四人組，還有三人組……

師：哦！原來人數可多可少，那你發現什么有意思的現象了嗎？

生2：蹺蹺板有的兩頭一樣高，有的一頭高一頭低。

師：蹺蹺板真吸引人，現在請一位同學和我一起體驗。

師：你的體重是多少？

生3：28千克。

師：我的體重是80 千克，請大家猜想一下，我和生3坐蹺蹺板是怎樣一幅場景？

生4：一定是生3坐的那端高高翹起來，老師坐的這端下沉落地，而且蹺蹺板根本無法上下來回晃動。

師：我們設法將蹺蹺板調節到平衡狀態，并嘗試用數學算式來解決這個問題。

生5：學生這邊需要增加2 人，只要新增的2 人的體重加起來達到52 千克即可，因為28+52=80（千克）。

師：需要保持平衡的不單單是蹺蹺板，生活中還存在其他類似的事物和原理。你首先會想到什么？（引導學生說出天平）

【設計意圖：基于學生的生活經驗，并以他們喜聞樂見而且熟知的事物為教學素材，讓學生通過提取自身的運動體驗來感受平衡現象，在觀察中領悟平衡的效應，并在師生互動中思考并弄清平衡的科學原理。如此設計，一方面為了消弭疏離感，讓學生興趣盎然地探究問題，熱切地去觀察、思考、議論，從而開闊眼界，順理成章地將生活中的平衡與數學中的等式搭建起聯系，讓數學學習變得充滿生活味，更貼近現實；另一方面也能激發學生的潛力，將學生的操作技能、生活經驗同步激活，誘使學生不斷反思追問，從生活經驗中去勘探和提取數學理論，為后續解釋“平衡”鋪好臺階。

方程的本質就是等式，等式可以用天平來模擬，但是這種模擬如果一開始就由教師提出來，那么學生就會喪失探究的主動性。因為天平是學生生活中很少接觸的計量工具，再加上天平本身也不是一種數學常用工具，學生對它缺乏基本的了解和認知。可見，直接引出天平則起點高、坡度大。要降低起點、放緩坡度，就為初級模型天平造一個更低端的現實模型——蹺蹺板，蹺蹺板是一種常見的生活素材，學生玩得多，也很了解，生活經驗可以直接轉換為數學活動經驗，從蹺蹺板的表征中抽象出天平模型，再從天平中抽象出方程，拾級而上，穩扎穩打，最終摘到方程這一“果子”。】

二、實踐，領悟平衡

1.活動，體驗平衡

師：通過擺開天平，你有什么切身感受？

生：天平左右兩邊不等重時，天平傾斜；左右兩邊等重時，天平平衡。

師：沒錯！天平時而平衡，時而傾斜。假若平衡，你能用數學式子表示嗎？（學生展示本組活動記錄，匯報算式：10克+10克=20克，20克+30克=50克……）

2.辨析，明晰平衡

師：你覺得這些式子都能客觀地反映平衡狀態嗎？它們都有哪些相同之處？

（學生重新審讀式子，發現里面都含有“等號”；式子左右兩邊的絕對值相等）

師：能用同樣的方法運用新符號來表示左右兩邊不等的式子嗎？

（學生小組合作探究，試圖寫出不等式）

【設計意圖：以操作活動為媒介，將數學學習融入操作活動中，一方面引導學生思考如何讓天平平衡，并通過觀察平衡情境寫出數學等式，這樣不僅能豐富學生認知，更能將平衡與等式聯系起來，而且還能引導學生從生活化思考轉向數學化思考：天平平衡代表什么？等式又代表什么？讓活動與思考相互滲透。另外，學生通過嘗試用新式子（不等式）表達不平衡狀態，認識到式子并非都是等式，也有不等式。平衡與傾斜的對比，強化了等式與不等式的對比，從而烘托出等式的特性，幫助學生建立天平與等式的聯系，形成扎實的記憶。整個活動豐富了學生的學習體驗，激活了學生的思維，更是建立了真實可信的表象工具——天平。

蹺蹺板的平衡經驗經過巧妙轉化，變身為天平的平衡經驗，學生將天平想象成簡易的蹺蹺板，兩邊的人被抽象成重物，學生在天平上通過放置重物調整平衡、體驗平衡，而且還可以用簡練的數學式表達，這樣基本就達到了等式的基本形態。學生在體驗中總結平衡的規律，發現平衡的現象放到式子里就是等式，等號就代表平衡，而等號的兩邊就相當于天平的左右兩盤，等號兩邊的數字就相當于放在兩盤中的重物，天平平衡代表等式。那么據此進行延伸，天平也可以不平衡，也就是傾斜，由此可以類推出一個式子——不等式，而傾斜又分為向左傾斜和向右傾斜，據此又可以類推出用“＞”和“＜”連接不等式。如此一來，等式和不等式就被同一個模型——天平“創造”出來了。】

三、探究，理解方程

1.借助天平，創設未知數

師：老師手里也有一組天平，你能根據已經掌握的知識嘗試寫出等式或者不等式嗎？

課件出示：

（學生依據情境圖，寫出相應的式子：①x+50＞100；②x+50=150；③x+50＜200；④x+x=200 或 2x=200）

師：請說出這些式子的由來。

（學生交流展示自己的想法）

【設計意圖：再次請出天平這個工具，利用學生熟知的環境來引出未知數。同時，利用4 組天平圖拓寬了學生的知識面，為引入未知數消除了障礙，并從學生熟悉的平衡、不平衡中，將未知數不露聲色地編入其中，毫無違和感。】

2.比較式子，引出方程

師：觀察根據圖1寫出的新的4個式子，與之前的對比，看看有沒有新的發現。

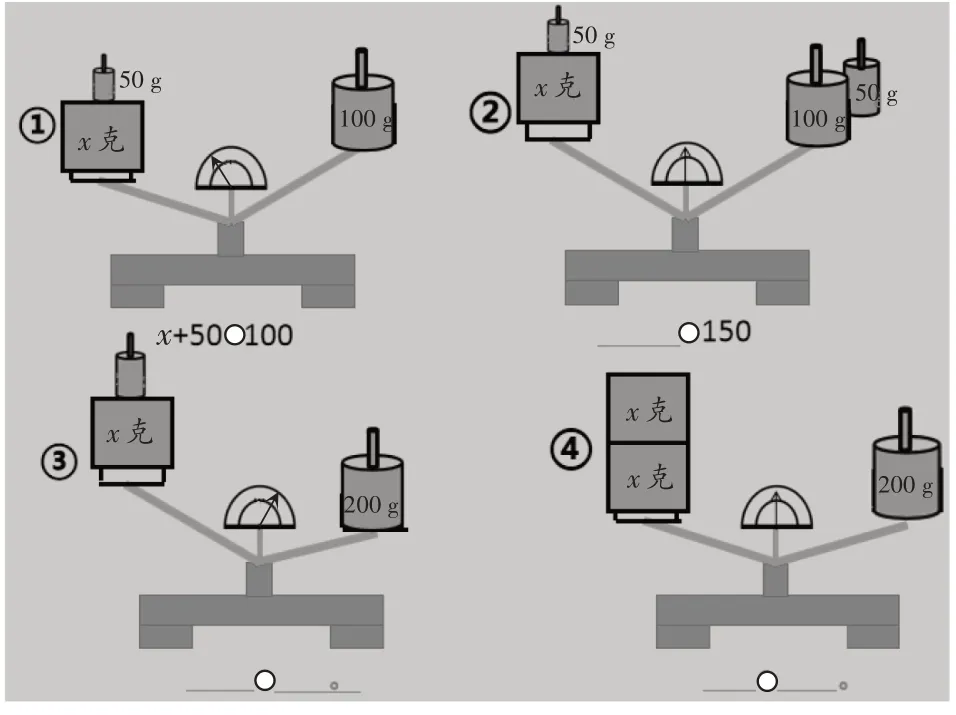
圖1

生1：前面的式子只含有數字，新的4 個式子卻含有字母x。

生2：前面的式子都有具體的數值，而后面的4個式子卻不確定。

生3：式子中的x是不知道的數，因此叫作未知數。

師：請查閱資料或者組內討論，看看“未知數”為何物。

（學生查資料并討論）

師：這4 個式子盡管都包含了未知數，但是否就意味著它們是一樣的性質？

生4：不一樣，①③兩個式子是用大于號和小于號連接起來的，而②④兩個式子是用等號連接起來的。

生5：像①③這樣用不等號連接起來的式子叫作不等式，像②④這樣用等號連接起來的式子叫作等式。

生6：像②④這樣的式子還可以叫作方程。

師：是的，像這樣含有未知數的等式又稱作方程。

【設計意圖：再次回歸天平這一模型，將其用足用活。用天平來表征不等式和等式，等式中又分為含有未知數的和不含未知數的，不等式中也分為含有未知數和不含未知數的，這樣，篩選方程的樣本大大擴充，辨別難度也大大提高，雖然迷惑性更大，但是卻可以突出方程的多層屬性，即方程首先屬于等式，然后屬于等式里含有未知數的那一類。】

3.解讀式子，領悟方程的意義

師：剛才有同學用到了一個新詞“方程”，究竟何為方程呢？

生1：含有字母的式子。

生2：必須是等式才行。

生3：都不對！像A+B=B+A就不算方程。

師：那么方程到底是何方神圣呢？

生4：必須和②④類似，同時滿足“是等式”和“含有未知數x”才行。

生5：我覺得只要有未知數就行，不一定非要是x，即使像（ ）+2=5這樣的式子也應算作方程。

生6：我同意。如a+8=10，b-25=56也是方程。

師：經過辯論，大家明確了什么？

生7：方程一定屬于等式，但是等式未必屬于方程，如1+2=3，因為里面不含有未知數。

生8：方程中必然含有尚未知曉的未知數，但并不一定是字母x。

生9：方程就是含有未知數的特殊等式。

師：你能自己編寫一道方程嗎？

（學生自主“編程”，并在組內討論，隨后教師展示學生作業，確定方程通用定義。）

【設計意圖：當學生能夠從紛繁復雜的式子中準確識別方程后，教師讓學生根據之前篩選方程的經驗和經歷，準確概括出方程的定義；然后又通過對照辨析，讓學生加深對方程的認識，弄清方程與等式的從屬關系，方程中字母的設定可以不受限，只要其為未知數即可，方程中出現的字母準確來說就是未知數，這個未知數與原來算式中代表空缺的“□”和“○”并無區別，例如“□+3=6”，本質上也是方程。這樣，學生對方程中的“未知數”“等式”等限定詞語有了更加全面、完整的認識和新的更高層次的理解。

經歷等式、不等式的對比辨析，慢慢揭示方程的本質，一方面能讓學生分清等式與不等式，另一方面還讓學生發現這些式子都包含字母x，并接受未知數的加入，把等式、未知數兩個概念融合成方程概念。同時，讓學生“編寫方程”，更是體現了數學學習的自主選擇性，讓學生接觸到最真實的知識面貌。】

四、引用，深化理解

1.審讀式子，歸類

（1）4+3y=10；（2）6+2a；（3）17-8=9；

（4）7-b＞3；（5）8x=0；（6）18÷a=2；

（7）3y+2x=15；（8）4×80=2x-60。

上述8 個式子中，屬于不等式的有（ ），屬于等式的有（ ），屬于方程的有（ ）。

2.判斷正誤

（1）等式都是方程。（ ）

（2）□÷8=8是一個方程。（ ）

（3）2x=0是一個方程。（ ）

（4）方程是含有未知數的式子。（ ）

（5）含有字母的等式叫方程。（ ）

3.編寫式子

（1）100元不夠買一件旗袍。

（2）320 元剛好買到4 本《哈利波特》。（嘗試用方程表示等量關系）

【設計意圖：通過各種形式的演練，學生進一步鞏固對方程概念的理解，明確等式、不等式、方程三者之間的勾連，從而真正認識方程、應用方程。三組練習題，第一組目的在于弄清界限，厘清概念的邊界；第二組是深層次理解并排除一些迷惑性的條件，加固對方程的已有認知；第三組是靈活運用方程概念來實施概念重構與檢驗，初步形成方程意識，也為后續列方程解應用題做好準備。】

五、反思，提升學習

師：本節課你學到了什么？等式、不等式、方程，你能說清它們之間的關系嗎？說說方程的基本特征，學會區分字母與未知數的細微差別。

師（小結）：方程可以解決很多用算術方法處理起來很棘手的問題。下面讓我們看看我國古人在方程上取得的驕人成就！（課件展示：《九章算術》相關知識）

【設計意圖：在課的尾聲，通過問答的形式梳理整節課所學的有關方程的全部知識，并在交流展示中加深學生對方程的記憶；課外拓展部分，增強了學生的民族自豪感。】