基于變導納柔順策略的康復機械臂示教研究

程 楊 潘尚峰 孫江宏

（清華大學機械工程系，北京 100086）

腦卒中具有高致殘率及高復發率的特點，約3/4的存活者存在不同程度的殘疾，且5 年復發率高達41%[1]，給家庭和社會帶來極大的負擔。積極規范的康復治療可以在最大程度上改善腦卒中預后，提高患者的生活質量[2]。康復機器人可以部分解決我國目前康復醫療資源不足的問題，它們大多儲存內置一些標準的康復動作庫，通過被動、主動康復等模式，輔助病人康復治療。但由于不同病人、不同階段的特異性，康復醫師會對此開具具有針對性的“運動處方[3]”，而這些動作不存在于標準康復動作庫，所以開發示教訓練十分必要。利用示教模式，可以將康復機器人的康復訓練與康復醫師的臨床經驗相結合，從而針對具體病人的實際情況，提供科學、高效的康復訓練計劃，顯著改善康復治療的效果[4]。

與采用人體動作捕捉設備[5]、雙目視覺測距[6]等方式采集康復示教動作相比，穿戴拖動示教不需要額外的采集設備，能夠降低系統的復雜性。康復醫師穿戴康復機械臂進行康復動作示教，機械臂在受控狀態下完成跟隨動作，在線保存軌跡數據，儲存康復動作，從而完成示教。在實際應用時通常采用Hogan N[7]提出的阻抗控制方法，使康復機械臂具有柔順特性，完成這一人機交互過程。

康復示教過程是動態時變的，固定參數的導納控制模型難以充分反應人機交互的特征，且隨著關節活動度的不同，人體關節的剛度也會發生改變。為保障拖動示教過程的安全性及跟隨性，機器人需要具有可變的柔順性[8]。變導納控制算法有模糊變導納、自適應變導納以及智能控制策略，如結合強化學習、神經網絡等方法進行變導納控制[9]。付興[10]等利用余弦相似度，模糊辨識機器人的狀態，如啟動、加速、高速穩定運動及減速等，不同狀態配以不同的阻尼參數，并通過試驗驗證了所提出控制方法的有效性，但其運動軌跡較為簡單，普適性較差。吳青聰[11]等利用模糊滑膜導納控制算法，改變系統導納參數，增強人機交互的柔順性，提高系統的舒適性。郝向陽[12]利用李雅普諾夫第二法構建系統自適應控制模塊，降低了拖動過程中的波動和干擾。杜志江[13]等提出基于模糊強化學習的變導納人機交互控制模型，結合個人操作因素，并運用于微創外科手術機器人的姿態調整，取得一定的成果。王飛[14]等提出根據環境剛度變化在線調節導納阻尼參數的方法，使得機械臂牽引跟蹤軌跡更加平滑，但機械臂為3 自由度，動力學模型耦合度較低。

針對示教過程中康復機械臂由于柔順性不足導致的隨動效果不佳的問題，本文設計了在關節空間內結合力矩微分項的導納控制器，并結合雙曲正切函數設計了改進的變導納控制策略，提高機械臂的柔順性，以期望獲得良好的跟隨效果。

1 康復機械臂介紹

為實現穿戴康復示教的目的，本文采用的康復機械臂如圖1 所示。康復機械臂具有4 個主動旋轉關節，1～3 號關節由3 個旋轉軸相交且相差60°的電機組成，用于模擬人體肩關節的運動自由度，4號關節用于模擬人體肘關節的自由度。這4 個自由度可實現人體上肢的肩部外旋/內旋、外展/內收、屈曲/伸展及肘部屈曲/伸展功能。每個電機的輸出端均通過輸出桿安裝一個BONGSHIN CDFS-100kgf拉壓力傳感器，用于間接測量人機交互力矩（圖2為以電機3 為例，拉壓力傳感器安裝示意）。

圖1 康復機械臂實物圖片

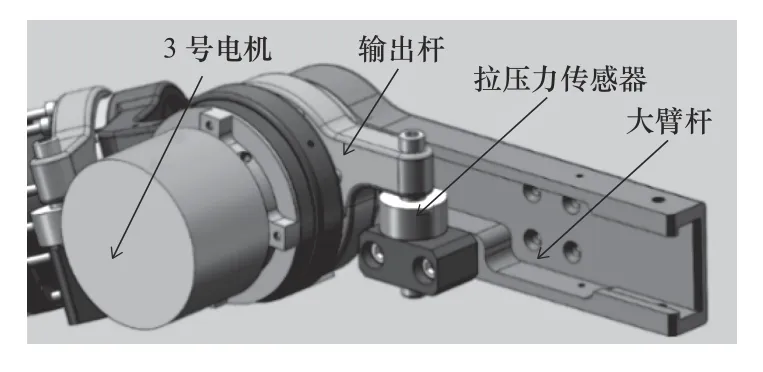
圖2 拉壓力傳感器安裝圖示

參照實際使用的材料及零部件尺寸建立康復機械臂的SolidWorks 模型，在肩心位置和每個自由度的旋轉中心沿電機輸出軸方向，建立了右手坐標系，并將得到的標準Denavit-Hartenberg 參數匯總在表1 中。

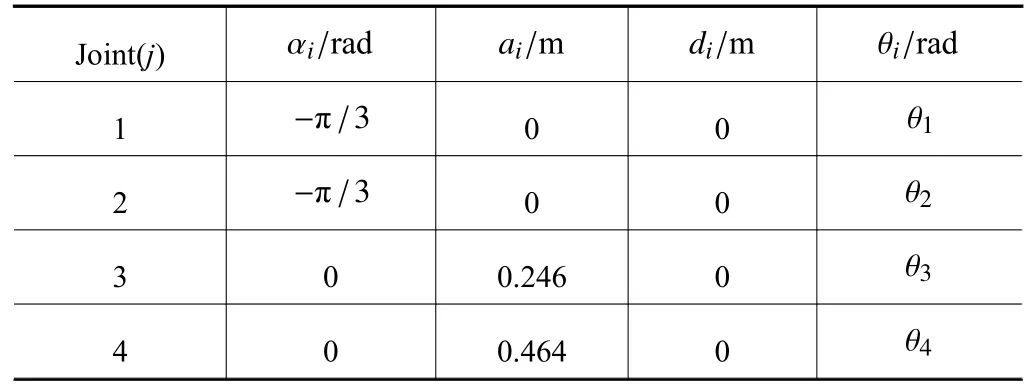
表1 機械臂標準DH 參數表

2 導納控制系統設計

2.1 導納控制原理及改進

結合本文采用的康復機械臂的特點，采用關節空間的導納控制。

根據導納控制的基本思想，將人體作為作業環境，則關節空間內，人體上肢與康復外骨骼機械臂的導納模型如圖3 所示。其中，τi是關節處的人機交互力矩，Ji為轉動慣性系數，bi為阻尼系數，ki為剛度系數，ke為人機交互剛度系數。

圖3 轉角形式導納控制原理

則有：

在示教過程中，康復機械臂處于自由運動狀態，故而設置ki=0,i=1,2,3,4 ，同時記Δ θi=θdi-θi，式（1）等效為：

為更好地改善人機交互效果、提高示教跟隨性及柔順性，引入人機交互力矩的微分項，從而增加導納控制器對人機交互力矩的敏感性并提高跟隨精度，對控制方程式（2）修正為：

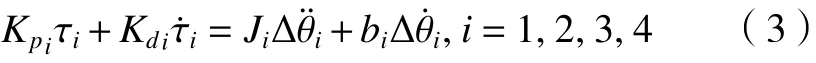
對式（3）進行拉氏變換，得到系統導納控制器的傳遞函數為：

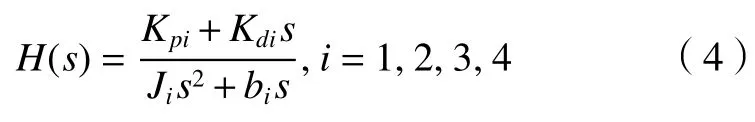
對于整個系統而言，其示教控制算法流程框如圖4 所示。

圖4 示教控制算法流程框圖

圖4 中，位置內環采用的是虛擬分解理論控制（virtual decomposition control,VDC）方法。使用者穿戴機械臂進行康復動作，通過拉壓力傳感器采集到人機交互力，再結合輸出桿長、電機輸出轉矩及各關節重力補償矩，計算出實際人機交互力矩，輸入到導納控制器中，得到機械臂各關節下一周期期望位置。結合反饋的機械臂各關節現有角度，作為位置內環的輸入，計算得到各關節所需的輸出扭矩，從而驅動機械臂到達所需位置。

2.2 基于雙曲正切函數的變參數導納控制算法

本文的變導納算法利用了雙曲正切函數（tanh），這是一種在神經網絡中常見的標準激活函數，具有完全可微分、反對稱、對稱中心在原點的優勢，保證了導納參數調整的平滑性。

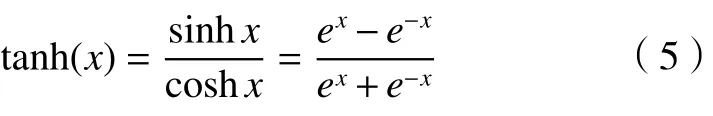
在實際人機交互過程中，需要關注的是交互力矩的絕對值大小，與方向無關，且雙曲正切函數的值域是(-1,1)，為實現變導納控制，對雙曲正切函數進行一定的變形處理。引入調整系數及對稱處理，得到新的調整函數 tanh(x)：

tanh(x) 及 tanh(x)的函數圖像如圖5 所示。通過調整參數m、n的值，可以對 tanh(x)的值域及集中度進行調整。m越大， tanh(x)的最小值越小。n越大，tanh(x)越集中，在0 附近的變化越快。

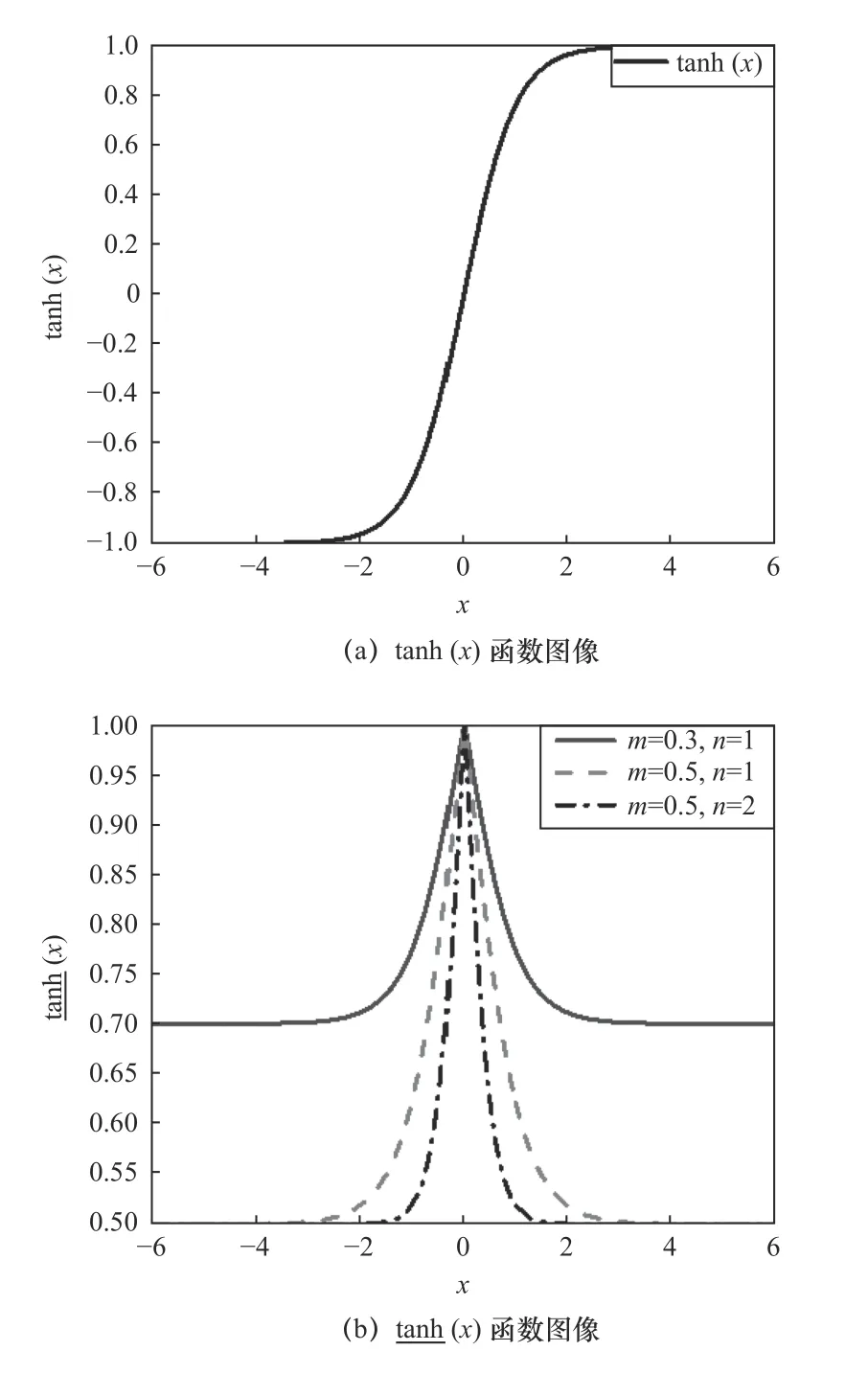
圖5 tanh(x)及tanh(x)的函數圖像

在具體的變參數導納過程中，轉動慣性系數J會同時引起系統固有頻率及阻尼的快速變化，其可調整的范圍有限，且會影響系統的整體穩定性[8]。在本文中采用對阻尼系數b進行調整。

當人機交互力矩變大時，降低導納控制器的阻尼系數，可以使康復機械臂快速提供較好的順應性，并改善系統的柔順性；當人機交互力矩變小時，導納控制器的阻尼系數較大，可以保證系統的穩定性及較高的位置控制精度。

利用調整函數 tanh(x)，則有

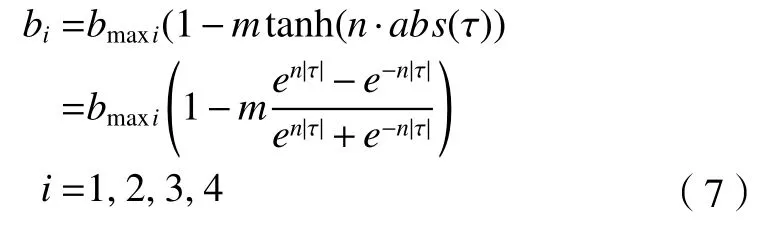
其中：bmaxi為bi的最大值，m為范圍調整參數，可以調節bi的最小值，n為變化率調整參數，用于調節bi的變化率。

根據二階系統模型的特性，為保障系統的穩定性，導納控制器還需要滿足以下3 個條件：

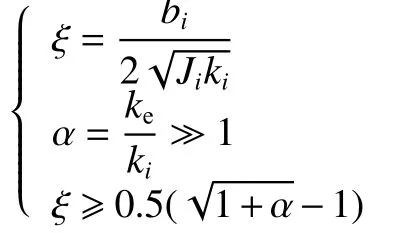
在示教訓練中，ki=0;i=1,2,3,4，則上述條件中，條件1、2 顯然滿足，條件3 等效有：

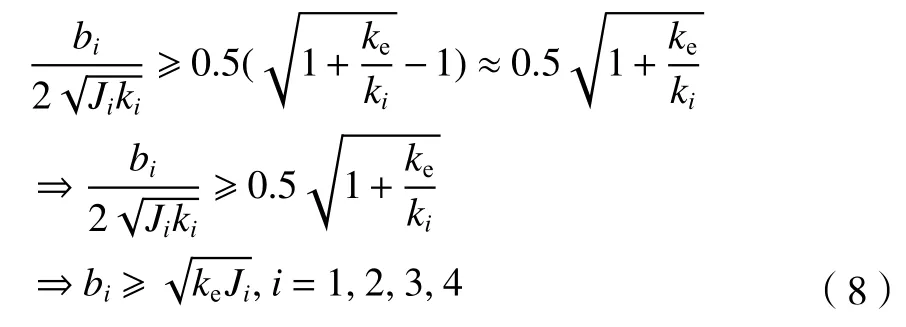
所以m∈[0,1)，且需滿足式（8）。

3 仿真平臺搭建及結果分析

3.1 仿真平臺搭建

為驗證提出的改進變導納控制器的有效性，利用機械臂SolidWorks 模型（圖6），采用Adams 與MATLAB/Simulink 聯合仿真，進行畫圓示教實驗。

圖6 機械臂SolidWorks 模型

先將SolidWorks 中配置有質量屬性的機械臂模型導入Adams 中，之后在4 個關節處創建旋轉運動幅，添加對應的旋轉運動驅動，定義扭矩、角速度等矢量方向。考慮到關節處摩擦力分析較為復雜，仿真時做了簡化處理。在Adams 中各旋轉運動幅設置最大靜摩擦因數為0.3、動摩擦因數為0.1。

利用Adams 中的Controls 插件，定義系統輸入為4 個旋轉幅的驅動扭矩（圖7 中tourque1～4），輸出為4 個旋轉副的旋轉角度及角速度（圖7 中q1～q4_dot），導出為m 文件，并在Simulink 中打開，如圖7 所示。

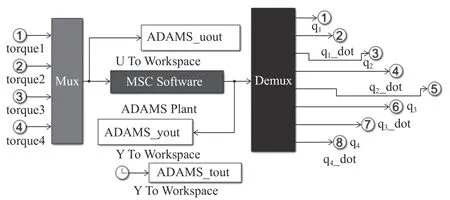
圖7 Adams 導出的控制子模塊

為引入人機交互力矩信息，假設環境剛度為ke，即康復機械臂實際運動角度與使用者的期望角度產生偏差時，為修正偏差，使用者在各對應關節施加的交互力矩有

結合控制流程框圖4，搭建圖8 所示的Simulink圖，其中棕色部分為Adams 導出的機械臂m 文件，用于進行動力學仿真；綠色的部分為系統的內部位置環，采用虛擬分解理論進行實現，具體如圖9 所示，輸入量為下一周期期望角度及當前周期機械臂實際運動角度，輸出為各關節所需驅動力矩，驅動機械臂到達期望位置；藍色部分為系統的導納控制部分，q1_r,q2_r,q3_r,q4_r 為使用者的期望角度。具體到adimittance模塊內部，由4 個各關節導納控制組成，以關節1 為例（圖10）。q1_r 為期望角度，q1_v 為當前位置，兩者差值乘以環境剛度ke，結合式（9）可以得到使用者的仿真輸入力矩TOL1，作為導納模型的輸入，在variable_admittance 模塊中，利用式（7），改變當前周期的阻尼參數b1，最終得到機械臂下一周期所需到達的位置q1_d。

圖8 系統仿真Simulink 圖

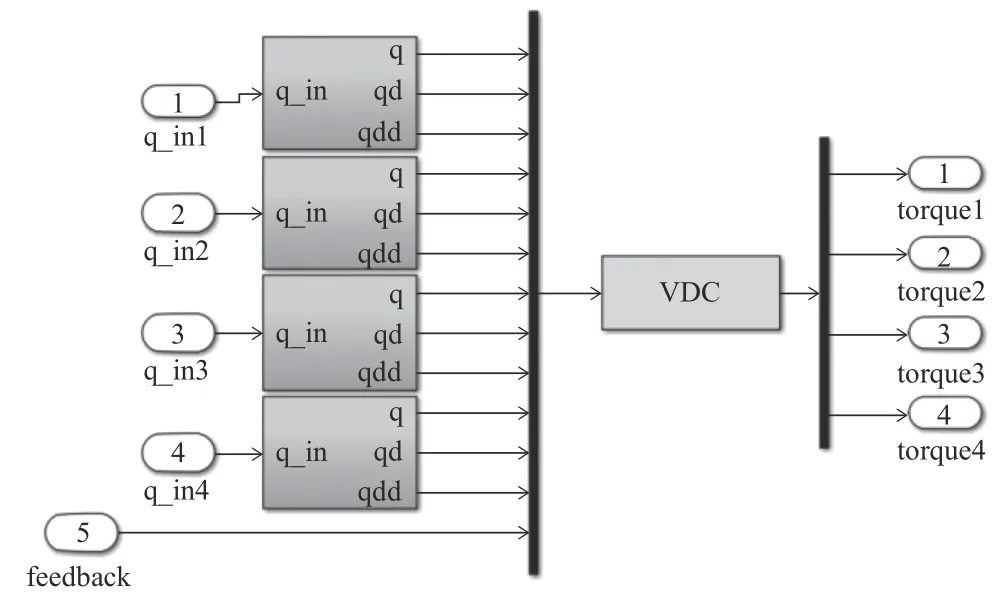
圖9 位置環VDC 控制

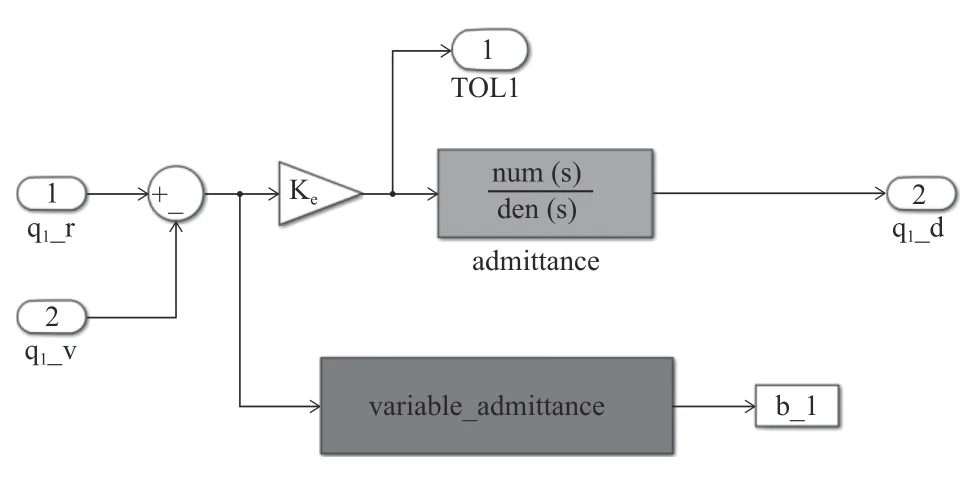
圖10 改進變導納控制器

仿真實驗期望動作軌跡采用笛卡爾空間下均勻畫圓，利用機械臂逆向運動學解出q1_r,q2_r,q3_r,q4_r 作為所需軌跡輸入，結合Adams 與MATLAB/Simulink進行聯合仿真。仿真實驗采用的主要參數為：

3.2 實驗結果與分析

實驗結果如圖11～13 所示。圖11 為3 種方法下的機械臂示教跟隨效果。在起始時有些許超調，之后康復機械臂跟隨性較好。

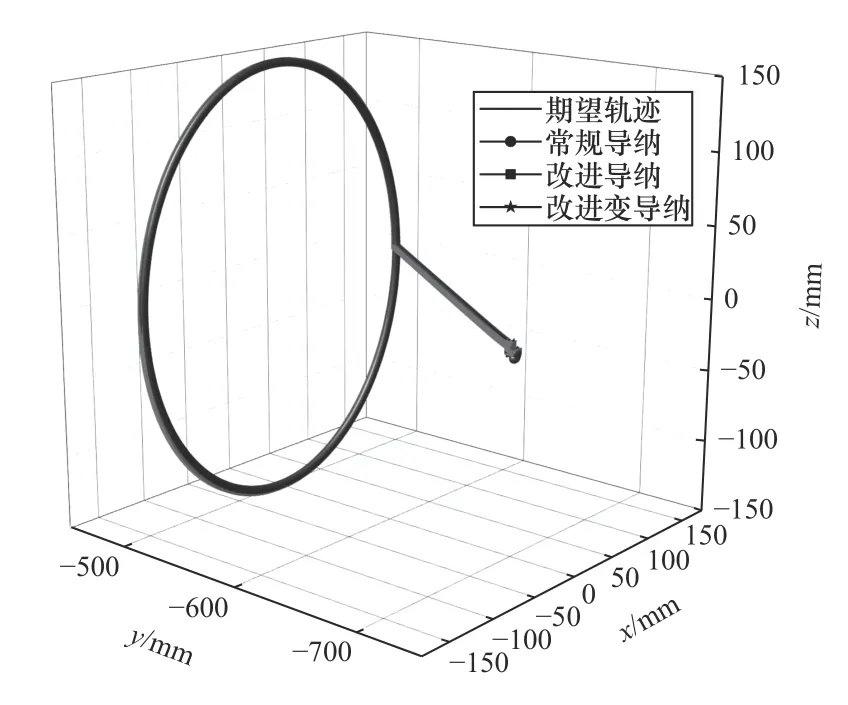
圖11 仿真實驗機械臂末端位置

圖12 為具體的機械臂末端位置在x、y、z這3個方向上的誤差，由于是在xz平面內畫圓，故而y方向誤差較小。誤差數據整理如表2 所示。在最大誤差絕對值方面，除起始時，改進導納及改進變導納控制器在x方向超調量較大外，后續過程中，兩種方法均可降低常規導納控制的跟隨誤差；在平均絕對值誤差方面，改進導納控制可以將常規導納的誤差降低到近一半，而改進變導納控制可以進一步降低機械臂的跟隨誤差，將機械臂末端位置跟隨精度控制在2 mm 以下，提高示教過程精度。

圖12 仿真實驗機械臂末端位置誤差

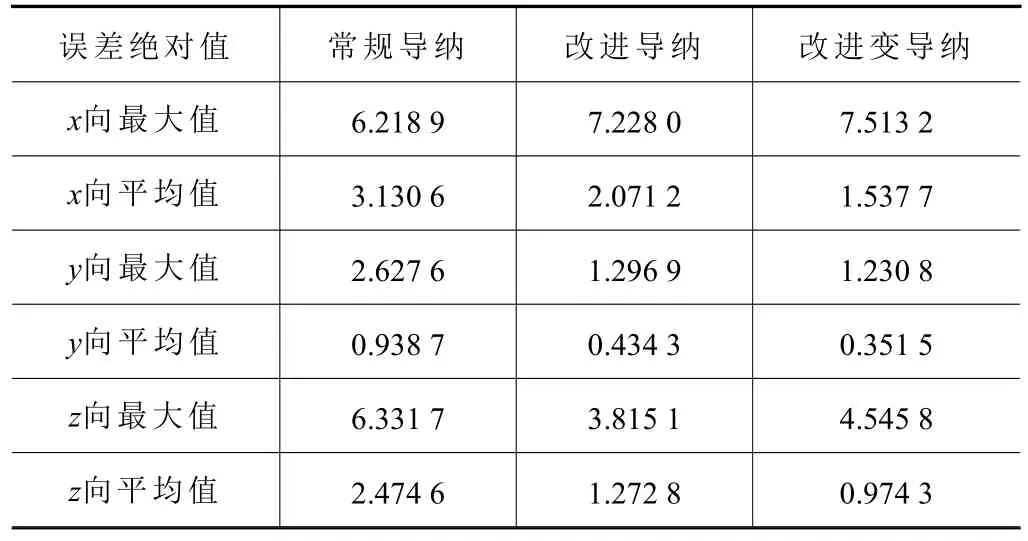
表2 仿真實驗誤差分析 mm

圖13 反映的是3 種控制方法下，各關節人機交互力矩的大小，整理分析數據見表3。在力矩峰值方面，改進變導納控制可以很好地降低力矩峰值，與常規導納相比，其關節1 交互力矩峰值降低45.30%，關節2 交互力矩峰值降低33.07%，關節3 交互力矩峰值降低10.99%，關節4 交互力矩峰值降低19.67%，大大減少了示教過程中使用者的負擔，提高了人機交互的舒適性；在人機交互力矩平均值方面，改進變導納的各關節平均交互力矩不到常規導納的一半，也進一步說明，在整個示教過程中，改進變導納方法更加輕便。

圖13 仿真實驗各關節人機交互力矩曲線

表3 仿真實驗人機交互力矩分析 N·m

4 實物試驗及結果分析

4.1 試驗裝置及過程設計

為進一步驗證上述理論的有效性，對康復機械臂系統進行實物畫圓示教試驗。利用實驗室開發的康復機械臂，在手臂末端固接一只馬克筆，白板上固定一個直徑180 mm的參考圓（圖14）。試驗過程如圖15 所示，實驗者通過穿戴康復機械臂，利用末端馬克筆在白板上參考畫圓，每次重復畫圓10 次。結合圖2，試驗時，穿戴者作用于機械臂，通過拉壓力傳感器采集數據，乘以輸出桿的長度，再減去機械臂關節輸出扭矩及各關節重力補償力矩，得到人機交互力矩，作為導納控制系統的輸入。實驗過程中，下位機通過串口上報上位機各關節角度及計算得到的人機交互力矩，上報周期10 ms。試驗參數除Kd=0.3外，其余同3.1 節參數設置。采用常規導納控制與改進變導納兩種方法進行穿戴康復示教試驗。

圖14 示教試驗平臺

圖15 示教試驗過程

4.2 實驗結果及分析

利用機械臂正向運動學，將采集到的各關節運動角度轉換為機械臂末端馬克筆的空間位置。記錄整理數據如圖16～18 所示。

圖16 常規導納控制法示教實物試驗畫圓

圖16和圖17 分別是采用常規導納控制方法和本文提出的改進變導納控制方法穿戴示教畫圓得到的結果。常規導納方法的多次畫圓之間重復性較低，且偏離參考圓較多。這一點也體現在表4 中。采用改進變導納控制方法，降低了跟隨誤差的最大值，且與常規導納控制方法相比，標準差降低11.46%，平均誤差絕對值降低25.09%。這說明采用改進變導納控制方法，使用者示教過程更加平穩，重復性較好，平均誤差也大大降低。

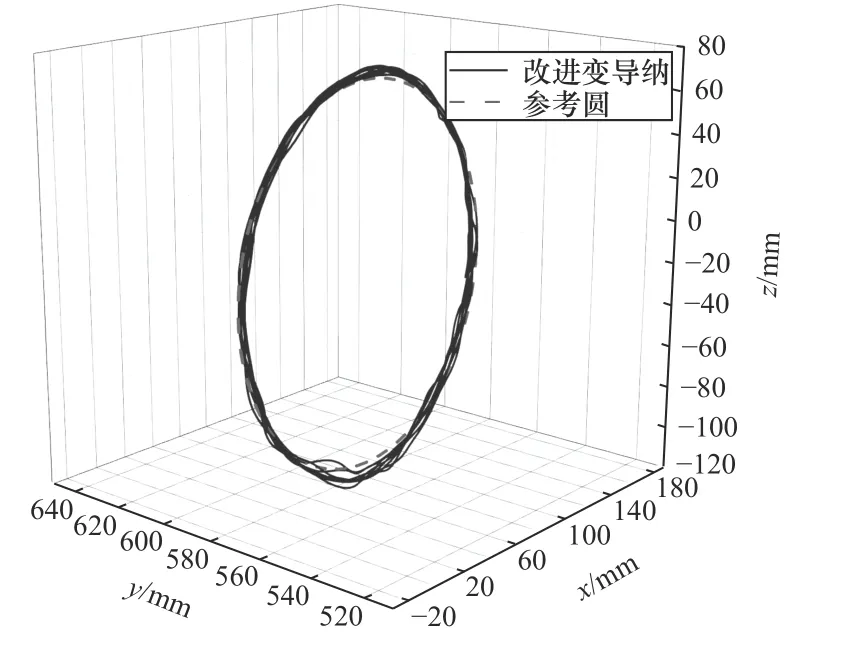
圖17 改進變導納控制法示教實物試驗畫圓

表4 實物試驗誤差分析 mm

各關節的人機交互力矩如圖18 所示，改進變導納控制方法在整體上比常規導納的力矩要小。分析人機交互力矩絕對值的特征信息匯總于表5。除關節1 兩種方法的區別不大外，在關節2～4 方面，改進變導納控制方法均在不同程度上降低了人機交互力矩絕對值的最大值、標準差及平均值，其中最大值方面以關節4 方面降的最多，降低了63.44%；標準差及平均值以關節2 方面降低最多，分別為23.27%及20.79%。結合輸出連桿長度為65 mm，示教過程中，使用者作用于各關節的力不超過2.23 N，示教負擔較小。

圖18 實物試驗人機交互力矩曲線

表5 實物試驗人機交互力矩絕對值分析 N·m

盡管新提出的導納控制器降低了常規導納控制的跟隨誤差，但仍然有平均2.462 6 mm的誤差。這主要有以下兩個原因：

（1）機械臂桿長的放大作用。串聯機械臂各旋轉關節均安裝有諧波減速器，系統具有一定程度的柔性，剛度較低，會導致位置內環的誤差。本文采用的機械臂僅小臂桿長就有470 mm，如果關節位置誤差精度控制在0.005 rad，轉換到末端空間位置誤差就有近2.35 mm的誤差。

（2）本文采用的導納控制器設計是基于關節空間的，但畫圓時，使用者通過目光觀察，接受到的畫圓誤差反饋是在笛卡爾空間下，其做力矩調整也是在x、y、z這3 個方向，而不是直接調整所需的關節角度，故而也會一定程度上增加系統的跟隨誤差。

但總體來說，本文提出的改進變導納控制器，可以將示教試驗畫圓平均誤差控制在2.5 mm 以下，能夠滿足康復示教訓練的需求，便于康復機械臂后續功能的開發。

5 結語

（1）針對康復機器人示教過程中跟隨效果不佳的問題，提出了關節空間下結合力矩微分項的導納控制方法，并創新性地采用雙曲正切函數實現變導納控制器的設計，提高機械臂的柔順性。

（2）利用康復機械臂的SolidWorks 模型，結合Adams 及MATLAB/Simulink 搭建了仿真實驗平臺，并進行畫圓示教實驗。仿真結果表明，提出的改進變導納控制器可以降低示教跟隨誤差，實現較高精度的示教過程，且人機交互力矩也較小。

（3）畫圓康復示教實物試驗結果表明，本文提出的結合力矩微分項的雙曲正切函數變導納控制器能夠很好地跟蹤示教者的動作，重復性好，降低了人機交互力矩，提高了系統的柔順性，改善了機械臂隨動效果。