基于變換序列權重峰值擬合的直線電機速度的快速精密測量

趙 靜，王婉婉，周 楊，董 菲

（安徽大學 電氣工程與自動化學院，安徽 合肥 230601）

1 引 言

直線電機由于其加速度大、定位精度高、結構簡單等優勢，是高檔數控機床的核心驅動部件，在高速精密加工、制造行業中得到了廣泛的應用［1-3］。對直線電機伺服系統而言，電機動子速度是重要的控制信息，其速度測量精度對于改善系統速度環的動態特性至關重要［4-6］。因此，研究一種簡單、精確的直線電機測速方法具有重要的實用價值。

系統速度反饋根據位移信息和信號采樣頻率獲得。目前，常見的直線電機動子速度測量方法采用光電編碼器、激光干涉儀等硬件傳感器。其中，直線光電編碼器測量精度較高，但環境適應能力差［7］。而光柵應用環境要求比較嚴格，不能承受較大振動，并且高精度光柵價格昂貴，維護困難，不適合長行程的直線電機［8］。雖然激光干涉儀測量精度較高，但其抗震性能差，并且成本較高，因此在機械加工現場較少使用［9］。針對特定場合下的直線電機測速，文獻［10］采用交叉感應線纜對大型直線電機磁懸浮列車進行測速定位，精度較高，但僅適用于文獻研究場景，限制因素較多。

數字圖像測速技術是近年來發展起來的自主測速方法，具有非接觸性、高精度和低成本等優點，廣泛應用于工業測量領域［11-12］。將它引入到永磁同步直線電機動子速度測量上，為動子速度測量提供了新思路。數字圖像測速方法主要分為光流法和序列圖像測量［13-14］。文獻［15］采用SURF提取特征點，通過改進的光流法對特征點進行檢測和跟蹤。然而光流法要求相鄰幀的亮度恒定，計算比較耗時，不具備很好的實時價值。相位相關比空域互相關法有更高的精度和可靠性［16］，文獻［17］利用超聲拍攝系統采集血管造影圖像序列，通過對連續兩幅圖進行圖像互相關計算位移矢量，進而得到血流速度；文獻［18］提出了一種基于奇異值分解（Singular Value Decomposition，SVD）的相位相關矩陣的運動估計方法。為了降低圖像信息冗余，文獻［19］將二維圖像單行采樣，利用改進的相位相關算法（Extended Phase Correlation Algorithm，EPCA），速度和測量精度均得到提高。但以上方法僅能在小位移內達到較高的精度，時效性仍有待提高。

上述測速方法均存在不足，因此本文以永磁同步直線電機為研究對象，設計了基于線掃描相機的電機動子測速系統，提出了一種基于連續一維信號和反比例權重峰值擬合的動子測速方法。首先，計算位移前后信號的歸一化互功率譜，使用傅里葉反變換得到狄拉克脈沖函數。然后，構造反比例函數代替狄拉克函數，使用峰值點和兩個鄰域點加權估算出相關幀的亞像素位移值。最后，根據設定時間間隔和標定系數，得到動子的平均速度，進而連續變換相關信號，得到直線電機的連續速度。

2 直線電機的圖像測速系統設計

本文設計的直線電機動子測速系統如圖1所示。

系統主要利用線掃描相機獲取底座上的序列條紋信號。在兩幀有重疊區域的位移前后信號f1（x）和f2（x）中，f2（x）可以表示為：

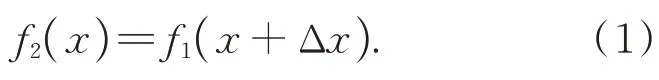
通過研究的亞像素測量算法，估計出兩幀之間的位移矢量Δx，在設定時間間隔Δt下，計算平均速度，通過連續速度關聯形成直線電機的速度狀態監測，動子的瞬時速度為：式中：x為圖像的灰度像素，v表示瞬時速度。由于設定的時間間隔極短，動子的平均速度近似等于瞬時速度。

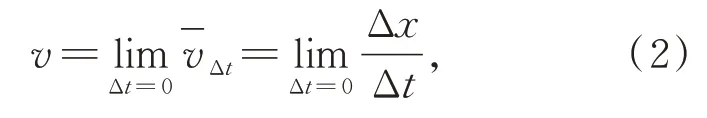
直線電機在做一維線性運動時動子往往會產生縱向抖動。如果是普通的二維灰度圖像，相機掃描目標圖像時會產生掃描偏差，因此需要將目標圖像的縱向灰度變化量置零，避免縱向振動的干擾。同時為了使圖像橫向灰度信息更豐富，本文構造出一種鋸齒波條紋目標圖像，如圖2所示。

圖2 鋸齒波條紋目標圖像Fig.2 Sawtooth stripe target image

沿著動子的水平運動方向，在底座上固定鋸齒波條紋目標圖像。在電機運動過程中，動子側面的線掃描相機實時掃描目標圖像獲取一維信號，如圖3所示。計算出動子的實際位移，在已知兩幀時間間隔下，即可計算出平均速度。對于直線電機動子運動平臺，由于獲取的條紋信號是連續并且能穩定地進行相位相關，因此可以得到連續的動子對地速度。

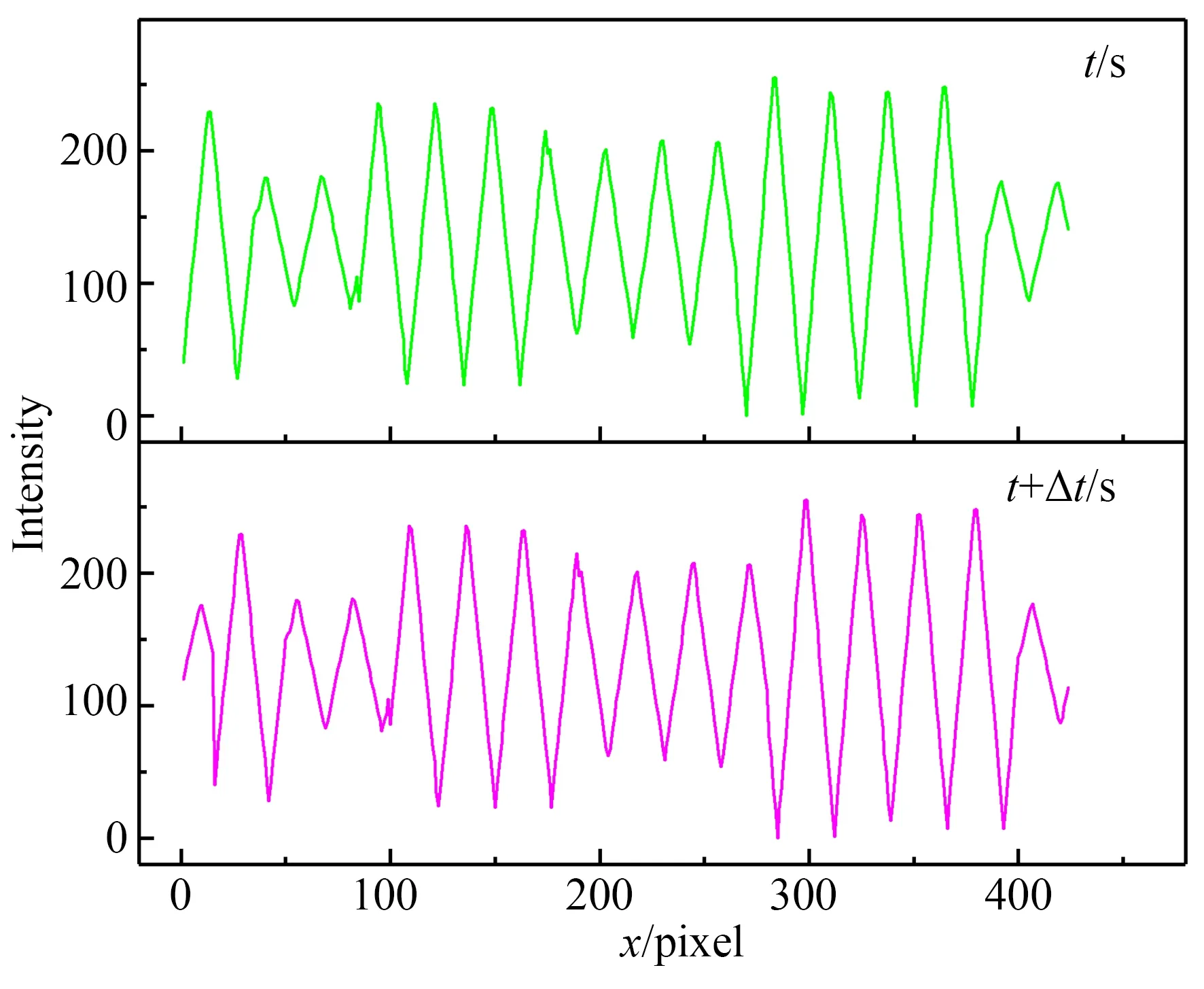
圖3 線掃描相機獲取的信號Fig.3 Signals acquired by line scanning camera

3 基于權重峰值擬合的測速方法

3.1 相鄰信號的直接相位差算法

直線電機動子在一維線性運動過程中，固定在其側面的線掃描相機在時刻t獲取到的鋸齒波信號為f（x），在時刻t+Δt獲取到的鋸齒波信號為g（x）。根據式（1）可知，f（x）和g（x）滿足：

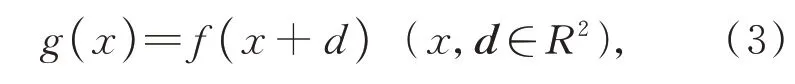
式中d為位移前后幀的像素位移矢量。

首先f（x）和g（x）計算相位相關，引入快速傅里葉變換（Fast Fourier Transform，FFT），f（x）和g（x）的傅里葉變換關系為：

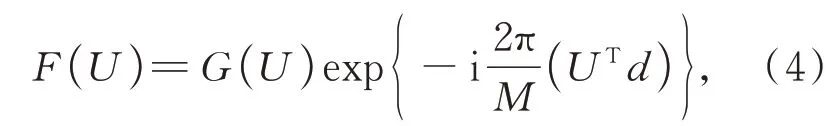
其中：G（U）和F（U）代表g（x）和f（x）的傅里葉變換，U是頻率域坐標，i是復數，M是圖像尺寸。為了得到相關幀的相位差，計算f（x）和g（x）的歸一化互功率譜，并對歸一化互功率譜做傅里葉反變換，得到：

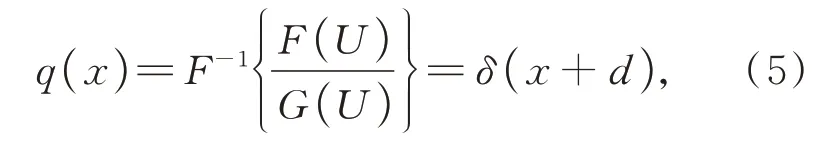
式中：F-1表示傅里葉逆變換，q（x）看作狄拉克函數。由于信號只存在一維x方向的運動向量，因此，理想情況下一維狄拉克函數在x方向上定義為：

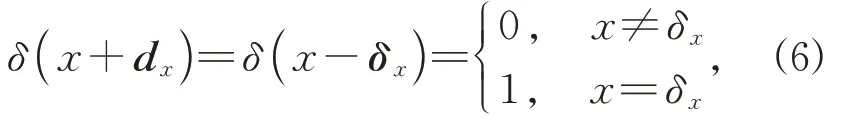
式中：δ表示變量為x，δx的分段函數，d x和δx表示x方向的運動向量。設定鋸齒波條紋相關幀位移d=15 pixel，即動子向左平移，拍攝的信號向右平移，計算的狄拉克函數如圖4所示。

從圖4可以看出，理想狀態下整像素平移后的脈沖函數的峰值為1，且脈沖函數出現在三維圖的一個平面上，一維互相關峰值的橫坐標是15 pixel，與設定位移d大小吻合。函數δ的峰值反映了相鄰信號的相關性，峰值越接近1，檢測精度越高。而當位移是亞像素時，脈沖函數峰值較低且出現較多的次峰。

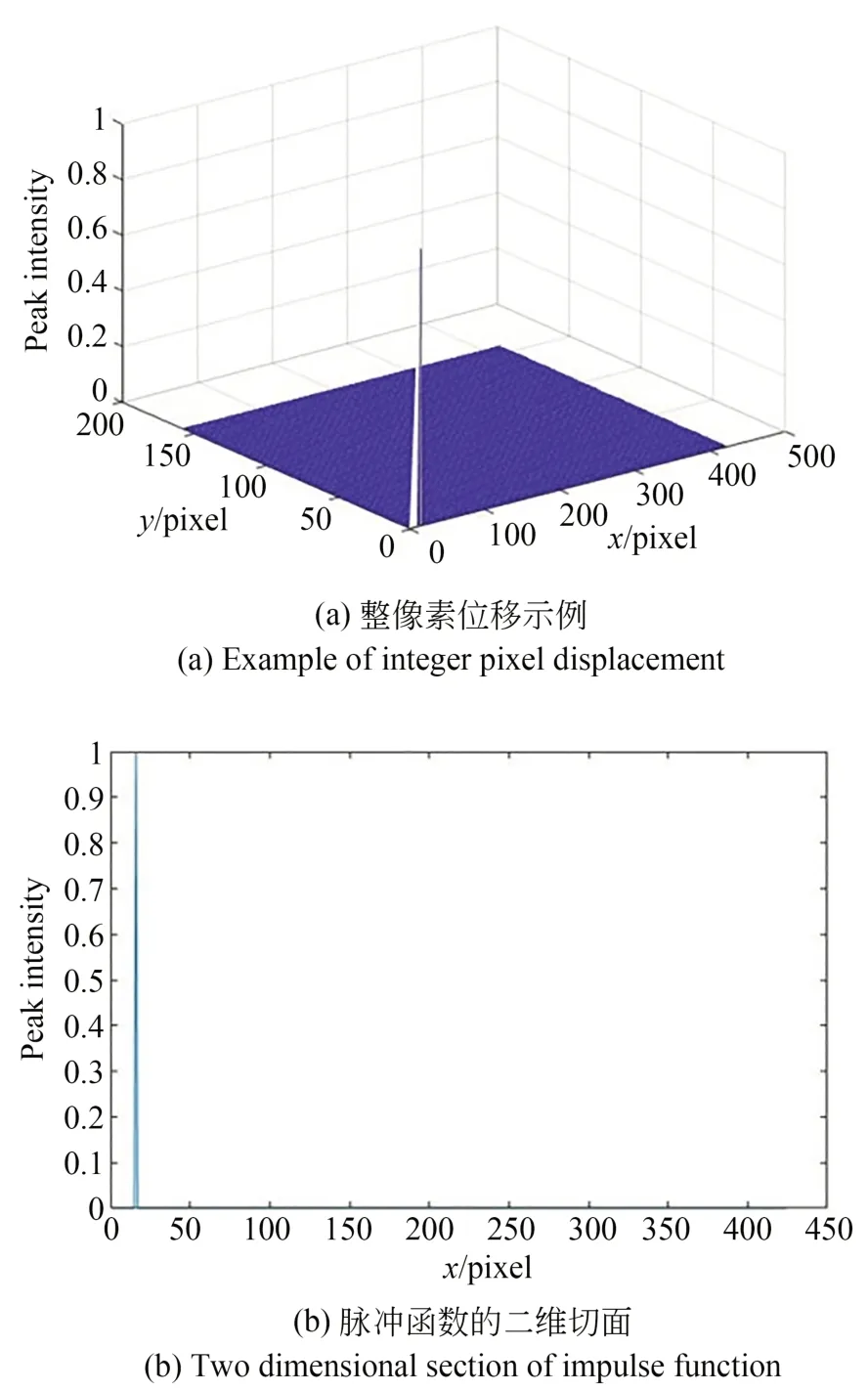
圖4 相位相關峰值Fig.4 Phase correlation peak

3.2 基于反比例函數的鄰域點加權精確擬合

本文引入可以用來計算圖像平移參數的反比例函數來替代狄拉克函數：

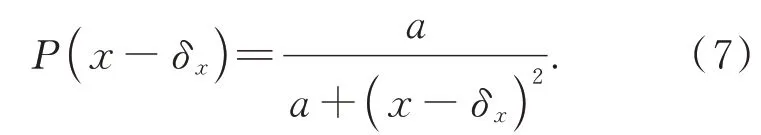
當a→0時，得：

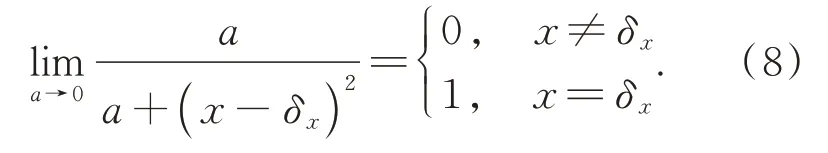
當a→0時，對式（8）進行積分，得：

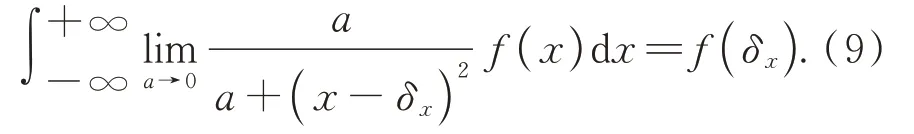
由式（9）可知，所構造的反比例函數滿足一維狄拉克函數平移性質，得到：

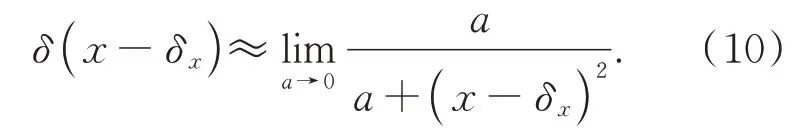
由式（10）可知，脈沖峰值位置只會出現在圖像的邊界上，即一維x方向上。整像素位移僅需一個峰值點就能確定，但亞像素位移會使脈沖函數出現多個次峰。在峰值點的相位差信號的能量值最高，若采用峰值點以外的鄰域點擬合，會增加計算耗時，并且擬合精度會受到旁瓣噪聲的干擾［20］。

為了確保精度和實時性，本文根據一維峰值點x=argmaxp（x）及其兩個鄰域點作為擬合陣列，得到：

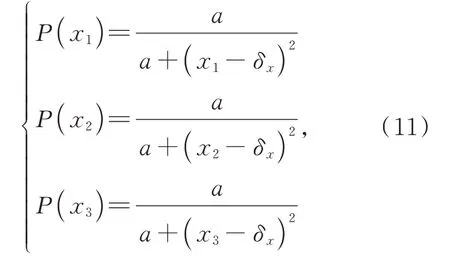
其中：（x2，P（x2））是x方向上的峰值點，（x1，P（x1））和（x3，P（x3））分別是左右鄰域點。緊接著P（x1）除以P（x2），P（x2）除以P（x3），得到：

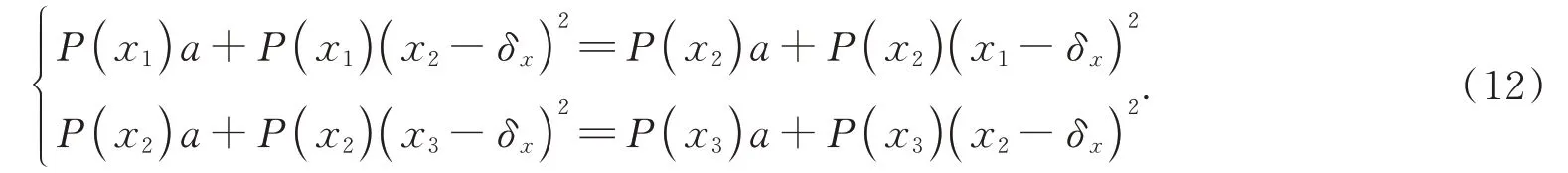
令a=0，得到：

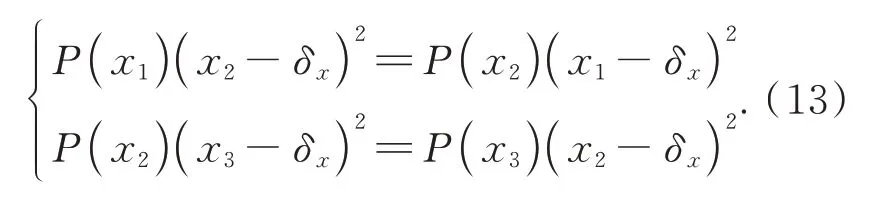
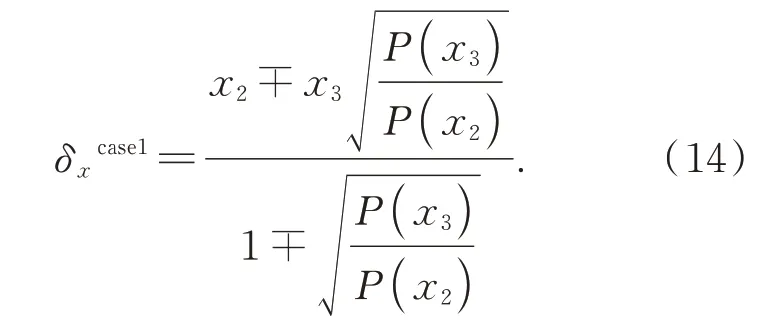
根據式（13），考慮存在以下3種假設條件：

（1）位移矢量在狄拉克函數的左邊緣，x1不存在。采用點x2，x3及其峰值P（x2），P（x3）擬合亞像素級峰值點，得到：

式（14）有兩個解，選擇x2～x3間的值作為最佳峰值點；

（2）位移矢量在狄拉克函數的右邊緣，x3不存在，采用點x1和x2擬合亞像素級峰值點，得到：

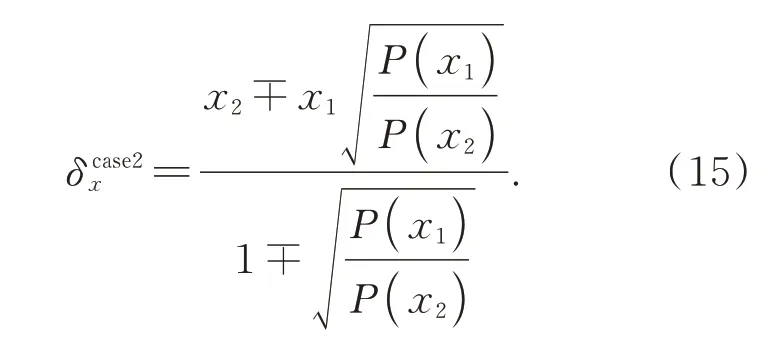
同理選擇x1～x2間的值為最佳峰值位置；

（3）位移矢量在狄拉克函數中心附近，則峰值點在x2的兩側。狄拉克函數具有對稱性，距峰值位置越近，函數值越大。因此按照峰值大小設定兩個準峰值位置不同的權重，來選擇最終的峰值位置。考慮前兩種情況，構建基于權重的擬合公式［21］如下：

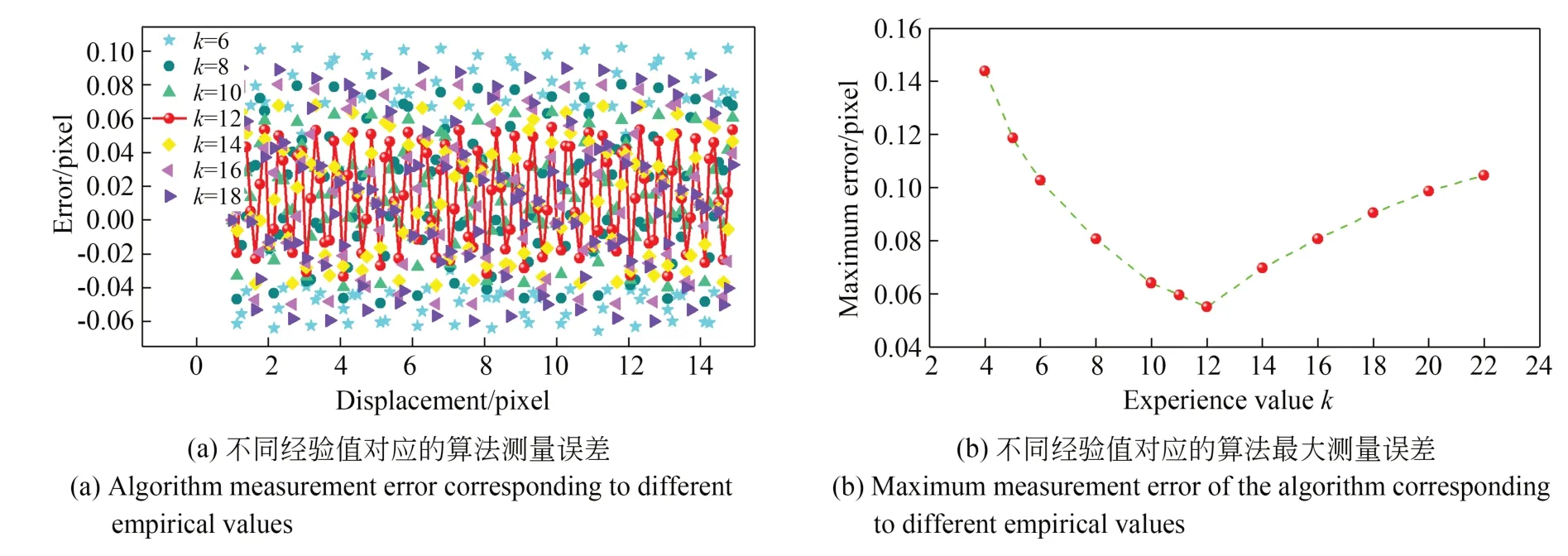
圖5 經驗值對測量精度的影響Fig.5 Influence of empirical value on measurement accuracy

式中w1和w2是權重函數：

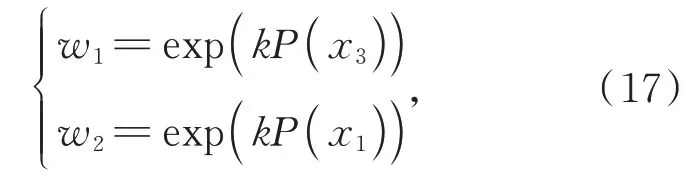
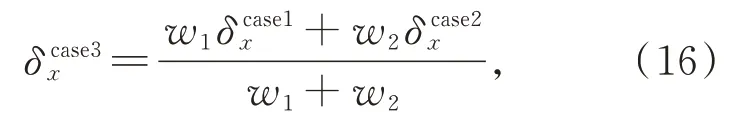
式中k是一個常數。

k的選取影響著權重值w1和w2，進而影響算法的測量精度。本文通過改變k值進行仿真實驗，計算測量位移誤差，如圖5所示。從圖5可以看出，當經驗值k取12時，此時算法的最大測量誤差值為0.055 pixel，精度最高，因此仿真實驗k值均取12。

3.3 速度計算

由于線掃描相機的行頻很高，設定拍攝幀頻為1 000 frame/s，則圖像信號的偏移量始終處于有限范圍內，f（x）和g（x）的互相關函數主峰位于中心附近。因此，利用本文提出的算法進行處理時，僅計算相關峰的鄰域有限點，即可計算出像素位移矢量。事先標定好相機像素的物理尺度s。在相鄰間隔時間內可近似認為直線電機動子是保持相對地面高度不變的勻速直線運動，那么動子的平均速度為：

速度方向由像素位移矢量方向決定。

4 仿 真

為驗證本文方法的有效性，在Matlab2017a中進行仿真實驗，電腦配置為：inter（R）i5-8250U，3.40 GHz主頻，8 GB RAM。

由式（18）可知，速度值相當于位移矢量乘以常量，因此對位移矢量的仿真測量就相當于對速度的測量，本文的測速方法對位移矢量的測量表現能夠體現出對速度的測量性能。將EPCA［19］，SURF［15］，MPF［20］，SVD［18］與所研究的權重相位相關峰值擬合（Weighted Phase Correlation Peak Fitting，WPCPF）方法進行仿真實驗對比，分別從運行時間、測量范圍以及精度魯棒性等方面進行驗證。

為了驗證本文算法的快速性，分別記錄上述5種算法每一次運行的耗時，進而繪制如圖6所示的算法耗時對比曲線。從圖6可以看出，WPCPF算法的平均耗時在0.019 8 ms左右，其計算速度遠遠高于其他4種算法，完全滿足線掃描相機的幀頻掃描要求。SVD和EPCA的平均耗時分別是0.018 s和5.79 ms。本文算法的效率比EPCA提高了至少100倍，在算法耗時上能夠滿足直線電機動子位置檢測的實時性要求。

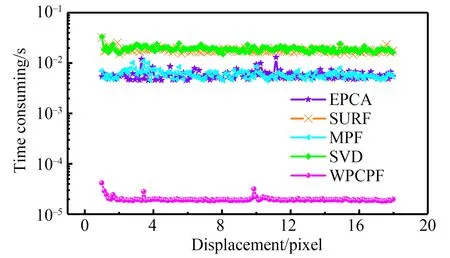
圖6 耗時比較曲線Fig.6 Time-consumption comparison curves

為了驗證WPCPF算法的位移測量范圍，與EPCA，SURF，MPF和SVD算法的測量范圍進行比較。以一定步長1.04 pixel對目標圖像進行位移設定，分別采用上述5種算法進行位移計算，測量結果如圖7所示。

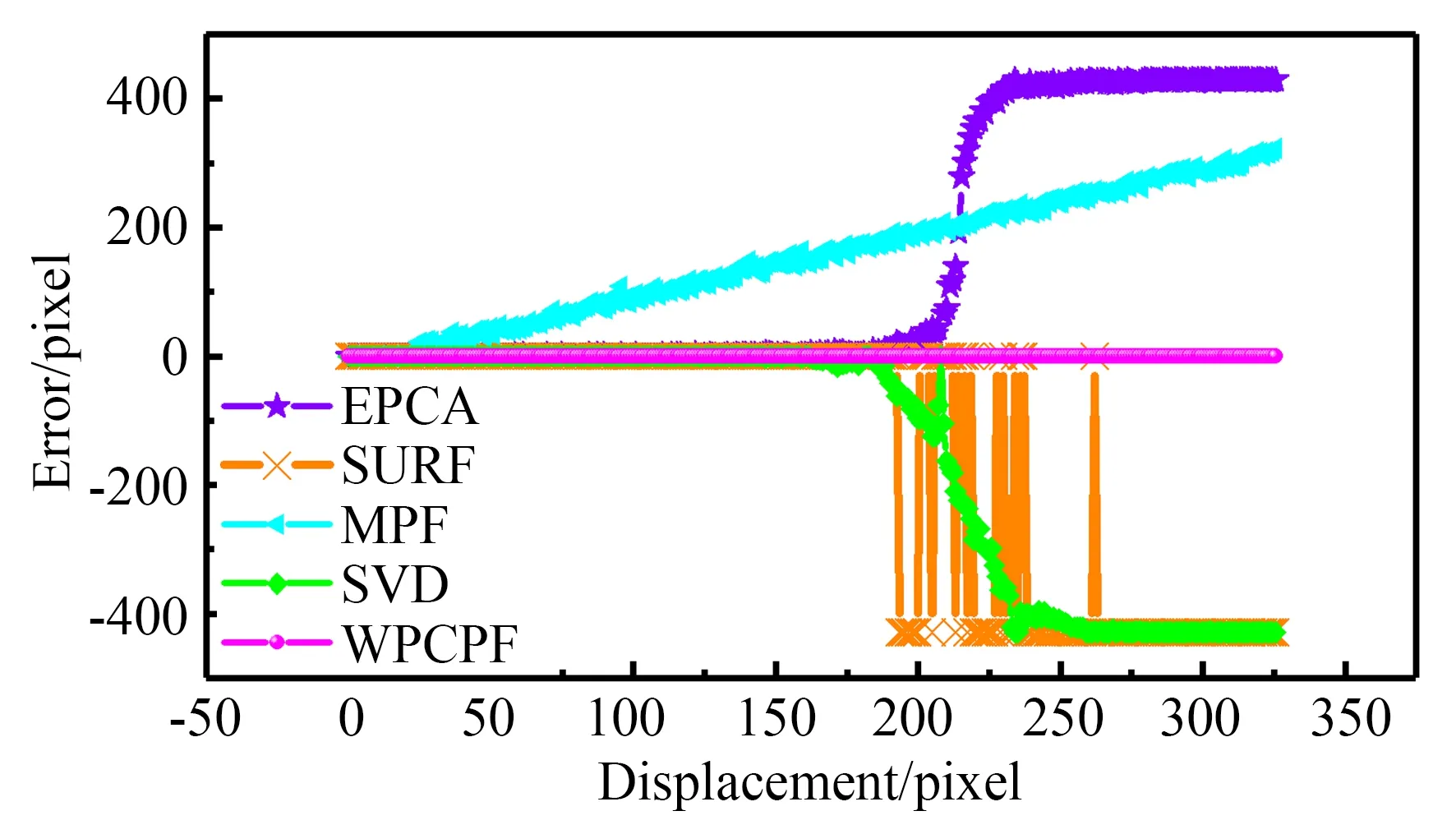
圖7 長距離下不同算法的測量精度Fig.7 Measurement accuracy of different algorithms in long measurement range

從圖7可以看出，在動子位移范圍較大的情況下，EPCA，SURF，MPF，SVD的測量誤差達到了400 pixel，即在較大的位移范圍內算法無法進行測量。其中，SVD，SURF和EPCA在位移接近200 pixel時誤差發生突變，無法實現亞像素測量。

而WPCPF算法始終保持亞像素測量，平均測量精度為-0.007 pixel，測量誤差為-0.05～0.03 pixel。因此與其他算法相比，本文算法可以實現更遠距離的測量，并且測量精度更高，滿足直線電機在速度較高情況下相關幀偏移較大的測量要求。

當位移值設定在一個較小的范圍內，驗證不同算法的測量精度，采用上述算法進行位移仿真測量對比，計算結果如圖8所示。

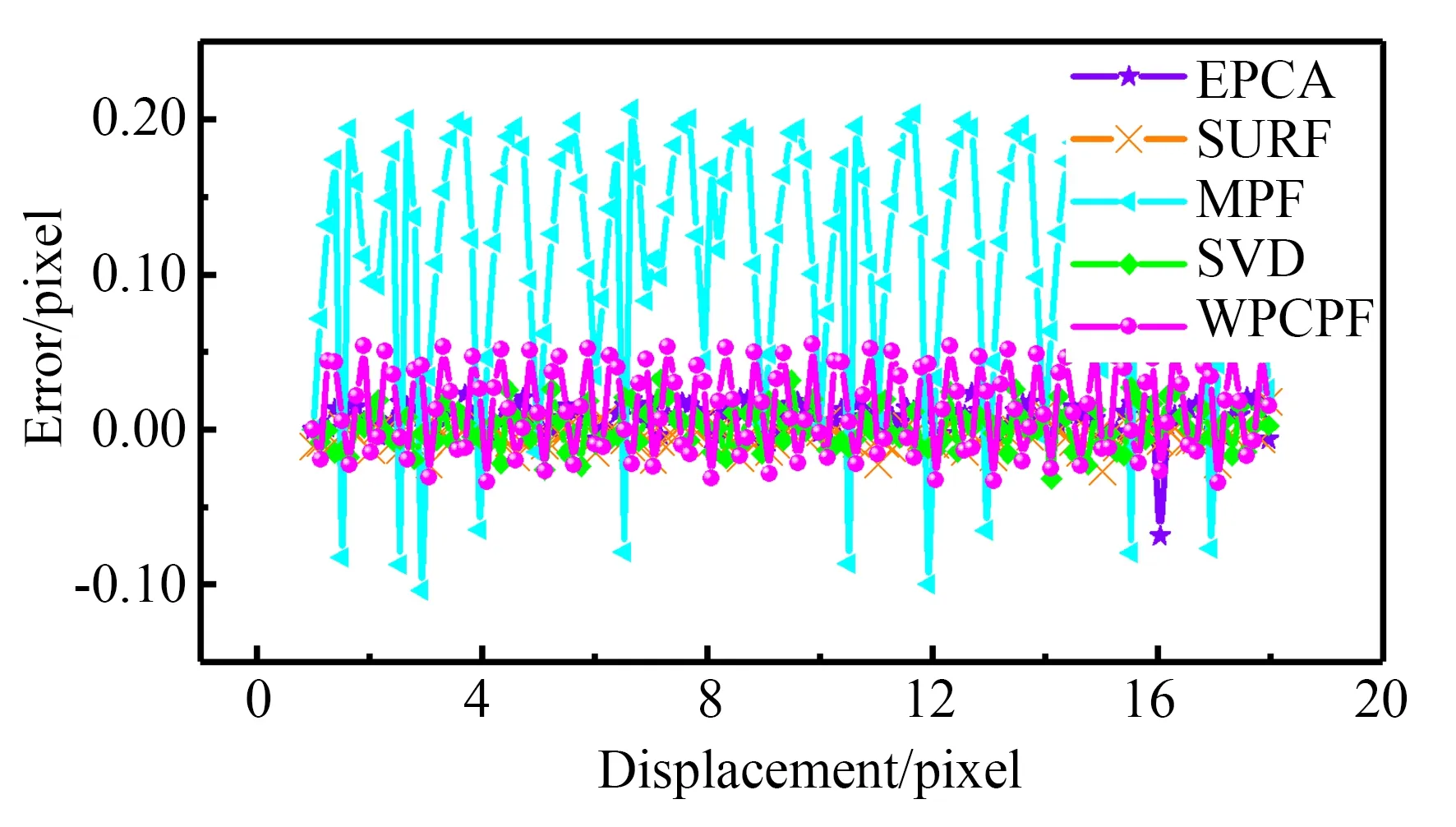
圖8 不同算法的測量精度Fig.8 Measurement accuracy of different algorithms

由圖8可知，EPCA的測量范圍為-0.068 74～0.023 35 pixel，其 平 均 測 量 誤 差 為0.007 1 pixel；SURF算法的誤差為-0.027 14～0.017 89 pixel；MPF算法的測量最大誤差為0.206 6 pixel；SVD進行亞像素位移估計時，其測量誤差的波動為-0.031 62～0.032 47 pixel。而本文算法在測量相關幀較小的偏移，其測量誤差為-0.034 32～0.055 1 pixel，測 量 精 度 達 到0.02 pixel。由此表明，本文算法具有較高的測量精度以及良好的測量穩定性。

為了驗證本文測量算法的魯棒性，對鋸齒波條紋目標圖像添加不同種類噪聲或不同強度的高斯噪聲，使用WPCPF算法進行位移計算，測量結果如圖9所示。

由圖9可知，隨著高斯噪聲強度的不斷增加，測量結果并沒有發生明顯的變化，本文算法仍然保持較高的測量精度。當高斯噪聲方差為0.08時，測量最大誤差在0.043 96 pixel，測量誤差波動較小且波動曲線并未發生突變。在椒鹽噪聲和散斑噪聲下測量的平均誤差為-0.011 pixel和-0.022 1 pixel。因此，WPCPF的測量結果穩定，對噪聲具有很強的抗干擾性，在進行真實噪聲的模擬環境下具有較強的魯棒性。

圖9 不同噪聲下的位移檢測結果Fig.9 Displacementdetectionresultsunder differentnoises

綜上所述，本文研究的權重相位相關峰值擬合算法在實時性、測量范圍、精度和魯棒性等方面優于傳統方法。

5 實 驗

5.1 實驗平臺的建立

為了驗證本文方法的可行性，搭建如圖10所示的實驗平臺。為方便實驗，固定優選出的鋸齒波條紋圖像，使之與線掃描相機的鏡頭相垂直。PMSLM的最大運行速度為1 m/s，有效行程為380 mm，線掃描相機的分辨率為1×1 024 pixel，幀頻為103frame/s。補光燈用以改變現場光強，照度計測量環境光強。當直線電機運動時，線掃描相機實時獲取含有運動信息的一維信號序列，然后將一維信號送到計算機使用WPCPF算法進行處理，并根據像素標定系數得到動子的速度。

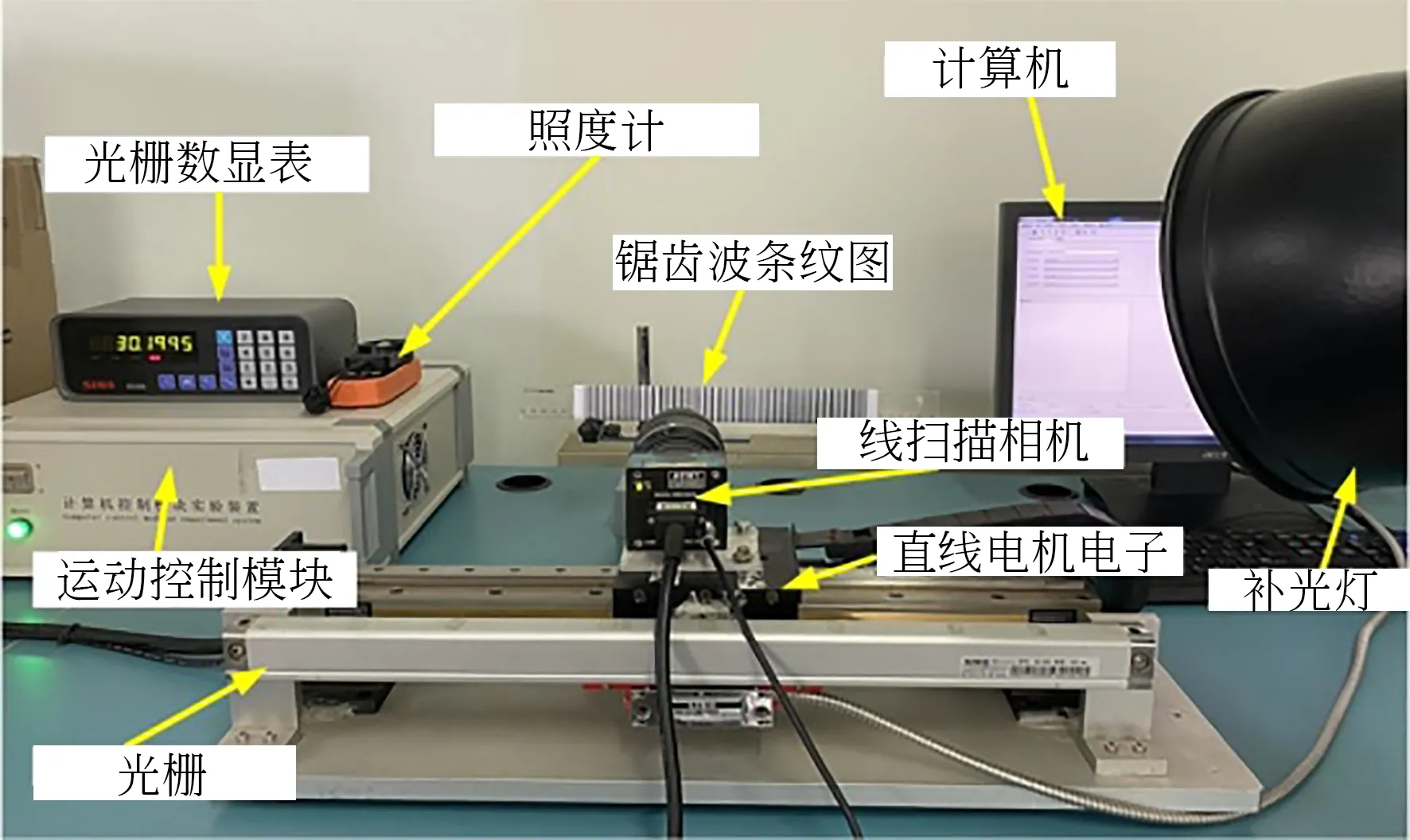
圖10 速度檢測實驗平臺Fig.10 Experimental platform for speed detection

實驗前，需要對動子的實際物理距離與像素位移值進行標定，采用棋盤標靶法進行系統標定，本 實 驗 的 標 定 系 數 是0.035 6 mm/pixel［22］。則動子的速度進一步表示為：

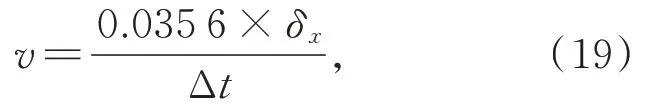
式中Δt是固定間隔時間，相關幀的物理位移距離為0.035 6×δx。因此，動子速度v的計算誤差主要來源于相關幀的位移計算誤差。

為進一步驗證WPCPF方法的正確性，設計兩組實驗：（1）動態位置精度跟蹤實驗；（2）動子速度的跟蹤檢測實驗。

5.2 實驗結果與分析

5.2.1 位置跟蹤性能

根據圖10的速度檢測實驗平臺，進行位置跟蹤實驗。為了驗證WPCPF方法的跟蹤定位精度，當給直線電機預設一些分辨率為1μm的位置脈沖時，條紋圖像序列被同步捕獲處理。然后，計算實際位置并與設定的運動值進行比較。預設軌跡如圖11（a）所示，并測量WPCPF方法的誤差，結果如圖11（b）所示。

通過比較圖11（a）中的設置運動軌跡，所提出的方法可以在誤差范圍內較準確地測量PMSLM的動子運動位置。從圖11（b）可以看出，該方法的測量誤差波動較小，3種預設的運動狀態的平均絕對誤差分別為0.026 87，0.022 5和0.021 4 mm。它的跟蹤性能方法進一步得到驗證。因此，該方法可以高精度跟蹤永磁同步直線動子的運動位置，并且提供了一種可以用于檢測直線運動目標運動軌跡的方案。

5.2.2 測速實驗

為了驗證WPCPF方法的測速精度，在實驗平臺上進行不同速度下的速度檢測實驗。保持現場光強不變，通過運動控制模塊改變電機速度，分別在0.3，0.5和1.0 m/s下采集運動信號，采用本文方法計算相鄰信號間的速度，實驗結果與分析如圖12所示。在電機運動過程中，采用WPCPF算法對實時采集的一維運動信號進行處理，對動子速度進行計算，運動速度測量結果如圖12（a）所示。將預設速度和測速結果進行比較，得到的測速誤差曲線如圖12（b）所示。

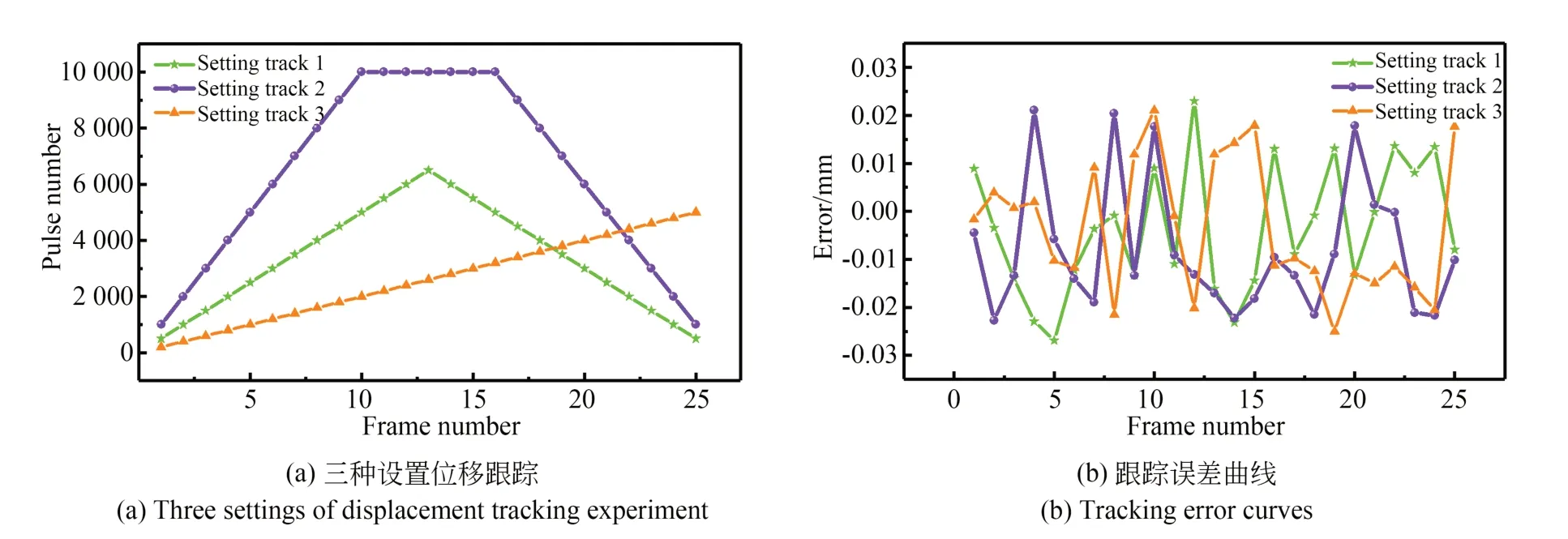
圖11 WPCPF跟蹤精度驗證Fig.11 WPCPF tracking precision verification

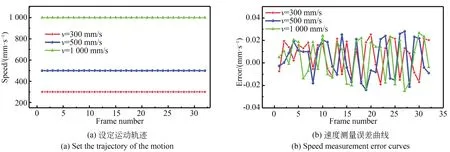
圖12 速度測量精度驗證Fig.12 Speed measurement precision verification

從圖12可以看出，當電機動子分別以不同速度穩定運行時，本文方法的測速精度保持在一個穩定的測量范圍。3種速度下的測速誤差分別為-0.019～0.025 mm/s，-0.024～0.028 mm/s，-0.025～0.027 mm/s。即使電機以最大速度1.0 m/s運行時，該測量方法也能保持穩定的測量結果。

綜上所述，在整個運動過程中測速誤差不大于0.03 mm/s，測速精度良好。從圖12（b）的測速誤差曲線可以看出，動子在3種不同速度下的速度誤差較小，能夠滿足較高的測速精度要求。

6 結 論

本文分析了光流法、互相關法和頻域擬合等粒子圖像測速方法的優點和限制，在此基礎上提出了永磁同步直線電機動子圖像測速系統的設計，采用線掃描相機進行拍攝，構造出鋸齒波條紋圖像作為目標圖像，研究了基于反比例權重峰值擬合的亞像素測量方法，應用到直線電機動子速度測量上，提高了測量的實時性，平均耗時約為0.02 ms。文中搭建了電機動子圖像測速實驗平臺，實驗結果表明，動子速度的測量精度達到0.03 mm/s，驗證了本文方法的可行性。