基于免疫多輸出支持向量回歸算法的隧道工程位移反分析新方法
宋 威,劉開云,梁軍平,徐 沖
(1.北京交通大學 土木建筑工程學院, 北京 100044;2.清華大學 環境學院, 北京 100084;3.中鐵第一勘察設計院集團有限公司, 陜西 西安 710043)
隧道圍巖位移的空間分布及隨時間的演化能夠表征圍巖的變形規律,在隧道工程的建設中,隧道位移的監控量測具有十分重要的意義,可以利用隧道位移值的絕對大小及其變化速度對隧道圍巖穩定程度進行判斷,而通過數值模擬的方法,能夠對隧道的變形過程進行模擬復現,供設計施工參考。而數值模型中參數的取值決定了數值模擬的精度,由于巖土體自身的物理力學性質復雜,受力變形過程具有高度非線性,所以準確識別巖土體的物理力學參數顯得十分重要。相較于通過經驗或工程類比的方法來確定參數,位移反分析方法提供了一種科學的、可控的參數取值方法,在巖土工程中得到了廣泛應用[1-3]。為解決正法反分析的計算效率問題,引入智能機器學習算法來對巖體復雜非線性系統進行建模,以代替數值計算,對反分析問題進行建模求解[4-7]。人工神經網絡和單輸出支持向量機作為位移預測方法,被廣泛地采用,取得了良好的效果。
位移反分析中的數值直接解法的精度取決于正向位移預測模型的精度和優化算法的問題尋優能力,關于機器學習模型,之前大多數研究采用的支持向量回歸模型均為一維輸出,只能滿足單變量的預測,對于隧道變形而言,一般在同一斷面監測得到的位移變量包括水平收斂和拱頂下沉,如果采用一維輸出SVR算法,就需要建立兩個單輸出的模型,在反分析過程中將水平收斂和拱頂沉降分開考慮,但這兩個變量實際上都是同一非線性系統的觀測值,兩者之間可能存在相互關系,而一維輸出SVR模型無法考慮這種相互之間的非獨立關系[8-9],本文引入一種針對多輸出系統(Multiple Output System)改進的支持向量回歸算法[10](MSVR),能夠在同一個模型中考慮多個輸出,建立統一的優化目標,進行模型訓練。引入該方法考慮水平收斂和拱頂沉降的相互關系,建立統一的反演目標。關于優化算法,近年來,許多優秀的集群智能優化算法被用來對反分析中的優化問題進行求解,而人工免疫算法是模仿人體免疫機制提出的一種新的智能方法,并在近幾十年來被廣泛的應用于非線性優化、組合優化、控制工程、機器人、故障診斷、圖像處理等諸多領域,并取得了一些成就[11-13],本文采用免疫克隆選擇算法(Immune Clone Select Algorithm, ICSA),對MSVR模型控制參數進行優化,使其對樣本的誤差最小,將其應用于隧道位移反分析中,結合銅黃高速公路三口隧道工程進行位移反分析,驗證該方法在巖土工程反分析領域的應用效果。
1 多維輸出支持向量回歸
1.1 一維輸出支持向量回歸
支持向量機學習方法是由Vapnik等[14]根據統計學的理論提出的。

(1)
式中:w為擬合系數;ξi,ξi*為松弛因子;C為懲罰系數;k為樣本數量。
約束條件為
(2)
式中:xi為第i個樣本輸入值;yi為第i個樣本輸出值;f為預測函數;ε為損失計算閾值。
對這一凸二次優化問題,采用Lagrange乘子法求解,Lagrange函數表達式為
L(w,b,ξi,ξi*,αi,αi*,γi,γi*)=
(3)

根據KKT條件,其對偶形式最大化函數表達式為
(4)
式中:xi為第i個樣本輸入值;xj為第j個樣本輸入值。
約束條件為
(5)
求解優化問題得到支持向量回歸模型,表達式為
(6)
式中:x為需要預測的樣本輸入值。
上述分析適用于線性回歸問題,對于非線性回歸,需要引入特征空間,使用一個非線性映射把數據映射到一個高維特征空間進行線性回歸,在高維特征空間用核函數來代替線性回歸中的內積運算,核函數的定義為
K(xi,xj)=φ(xi)·φ(xj)
(7)
式中:φ為非線性映射函數。
經過與線性回歸相同的推導,最后得到的支持向量模型擬合函數為
(8)
核函數種類較多,徑向基函數核函數(Radical Basic Function,RBF)是一種常用的效果較好的核函數,表達式為
(9)
式中:x,y為兩樣本輸入值;σ為核函數參數。
1.2 多維輸出支持向量回歸
傳統的支持向量回歸的輸出變量為一維變量,該特點使其應用場景受到限制,在一些復雜的系統里,需要建立多輸入-多輸出的映射系統,而一維SVR并不能完成此類任務,因此,文獻[10]在一維SVR的基礎上進行擴展,使其適用于多維輸出系統,以解決實際工程中更為復雜的問題。
將一維ε不敏感損失函數擴展到多維,定義損失函數,表達式為
(10)
基于式(10)所示損失函數,構造優化目標函數,表達式為
(11)
為解決MSVR模型的數學優化問題,文獻[10]中提出了采用迭代加權最小二乘法(Iterative Reweighted Least Squares)來求解。
在式(11)的優化目標函數中,將損失函數用一階泰勒展開來近似替代,即
(12)
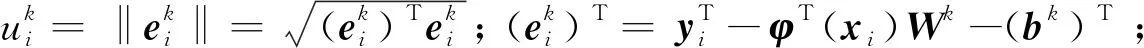
構造式(12)的二次近似代替,文獻[10]中采用的近似公式為
(13)
式中:CT為不依賴于W和b的常數項。
采用近似公式(13)的原因是該公式中W和b解耦合,優化求解不需迭代,直接取對W和b的偏導數等于0即可計算出W和b的近似解。
算法流程如下:


Step3計算下一迭代步的解,迭代計算公式為
(14)
式中:ηk為迭代步長。
采用回溯算法來確定迭代步長。每個迭代步的初始步長設置為1(初始步長的選取對于算法的收斂非常重要),然后檢查LP(Wk+1,bk+1) Step4計算uik+1和αi,設置k=k+1,回到Step2,直到滿足收斂條件,達到收斂。 優化目標求解完畢得到使樣本集合總體損失最小的W和b,多輸出支持向量回歸模型即建立完畢,多輸出支持向量回歸稱為MSVR。 生物免疫系統是一個復雜的自適應系統。人體免疫系統能夠識別病原體并做出應答反應,從而具有一定的學習、記憶和模式識別的能力。可以將其信息處理的原理、機制采用計算機算法進行描述,來解決科學和工程問題。Castro[15]最早提出了克隆選擇算法 (ICSA),該算法是受人體免疫系統啟發,模擬生物免疫系統功能和作用機理對復雜問題進行求解的智能方法,它保留了生物免疫系統所具有的若干特點,包括全局搜索能力;多樣性保持機制;魯棒性強;并行的求解搜索過程。將其引入對優化問題進行求解。 在ICSA算法中加入了種群抑制過程,來對種群的平均濃度進行控制,避免算法過早的收斂到局部最優解,增加全局優化能力。ICSA算法的詳細過程見圖1。 圖1 ICSA算法流程圖 采用典型多峰函數Rosenbrock函數(香蕉函數)檢驗改進后的ICSA算法的優化能力,其函數表達式為 (15) 式中:X=[x1,x2,…,xn]∈RN Rosenbrock函數全局最小值點在所有自變量取值為1時取得,函數值為0。用10元Rosenbrock函數檢驗ICSA算法對于多元函數的優化效果。自變量的搜索區間為(-10,10),算法參數設置見表1。 表1 優化算法控制參數取值 運行10次優化算法,大約4次找到函數的最小值點,這10次的優化結果見表2。由表2可知,ICSA算法具有良好的多維多峰值函數的尋優能力,可以應用于求解MSVR模型的優化問題以及基于ICSA-MSVR耦合算法的巖體物理力學參數位移反分析。 表2 Rosenbrock函數優化結果 MSVR模型的建立過程中,控制參數(懲罰系數C,敏感系數ε,核函數參數σ)的取值需要人為指定,為了控制參數取值來達到最小的樣本訓練誤差及最好的MSVR模型泛化精度,采用ICSA算法對參數進行優化求解。 在模型訓練階段,定義訓練樣本集合的總體誤差函數為優化目標,單個樣本的誤差同樣采用ε不敏感損失函數,見式(10),將訓練樣本分為學習樣本和測試樣本,采用K折交叉驗證的方法來計算樣本整體誤差,優化目標函數表達式為 (16) 式中:Lall(C,ε,σ)表示整體的訓練損失函數;k表示樣本等分的份數;km表示訓練樣本k等份后每份的數量;上標星號表示求得的最優參數。 待MSVR模型訓練完畢,即通過ICSA算法優化求得最優的MSVR模型參數后,即完成正法反分析過程中的位移預測模型的建立過程。 MSVR模型建立完成后,可以進行巖體的物理力學參數辨識過程。 給定待反演巖體物理力學參數的取值范圍,優化目標函數為預測位移(拱頂沉降和水平收斂)的誤差函數,其表達式為 (17) aff(x)=[fu(x)-u]2+[fv(x)-v]2 式中:x為待反演參數向量,即圍巖的物理力學參數,選取的7個參數為重度、變形模量、黏聚力、內摩擦角、水平側壓力系數、泊松比、剪脹角;fu(x)為MSVR模型預測水平收斂;fv(x)為MSVR模型預測拱頂下沉;u為現場實測水平收斂;v為現場實測拱頂下沉;aff為親和度函數(即優化目標函數,最小化問題)。 優化完成后輸出優化結果,完成參數反演,得到巖體力學參數的辨識結果。 將辨識參數輸入到MSVR模型中,對隧道開挖的后續位移進行預測。以驗證辨識得到的參數是否符合工程實際。 ICSA-MSVR耦合算法的流程見圖2,在定義誤差函數和結果輸出部分模型訓練過程和參數辨識過程有所不同。 圖2 ICSA-MSVR耦合算法流程 在ICSA算法的優化過程中,為了擴大參數的搜索范圍和搜索效率,將待優化參數進行了指數映射,即在種群中的參數的取值范圍是實際的取值范圍的自然對數,在實際親和度計算中,將抗體個體進行指數映射,計算公式為 P′=exp(P) (18) 式中:P為每個個體的取值(對于模型訓練過程P為三個支持向量回歸控制參數C,ε,σ,對于力學參數反演過程P為待反演的7個巖體的物理力學參數)。親和度計算采用指數映射后的個體取值P′。 銅(陵)—黃(山)高速公路銅湯段三口隧道為雙向分離式四車道高速公路隧道,左、右線隧道間距約為46 m,左線隧道超前右線隧道施工,超前距離約為30 m,因而可以忽略右線隧道施工對左線隧道的影響。本文考察其左線出口段。該段為Ⅲ級圍巖段,里程樁標號為ZK252+270—ZK252+511段,軸向掘進總長度約為241 m。 三口隧道施工方法為爆破掘進開挖,隧道研究段為全斷面一次開挖,以3 m為循環進度,每天掘進6 m。在隧道施工過程中設置監測斷面,對隧道收斂和沉降變形進行監測,ZK252+510監測面測點位移見表3。 三口隧道橫斷面見圖3,通過Midas建立網絡模型,然后導入FLAC3D中進行計算,整體數值計算模型見圖4。采用均質材料的假設,沿隧道軸線方向為y軸方向,垂直向上為z軸方向,x軸水平向右為正方向,模型從左至右寬為60 m;從坐標原點往下長為50 m;計算模型沿縱向長80 m,單元共42 500個,節點共43 768個。 圖3 三口隧道斷面(單位:m) 圖4 三口隧道數值計算模型 對模型前后左右及下邊界施加法向變形約束,上邊界為自由邊界。由于沒有實測地應力資料,垂直地應力等于上覆巖層自重。兩個水平方向地應力相等,等于豎向地應力乘以水平側壓力系數。 隧道初期支護采用噴錨支護,噴射混凝土采用C25混凝土,厚度10 cm,錨桿布置長度為2.5 m,環向間距1.5 m,錨桿采用全長粘接水泥砂漿錨桿,鋼材為HRB335,直徑為25 mm。錨桿鋼材和C25噴射混凝土的本構均為彈性本構,參數見表4。錨桿數值模型見圖5。 表4 隧道初期支護材料力學參數 隧道采用全斷面開挖,數值模擬中循環進尺為3 m,初期支護緊跟掌子面。變形監測斷面設置在距離隧道出口處1 m的位置。變形監測點見圖6。 圖6 變形監測點布置 參考JTG D70—2014 《公路隧道設計規范》[16],圍巖物理力學指標見表5。 表5 圍巖物理力學參數取值范圍 我國地應力實測資料表明水平側壓力系數范圍為0.55~2.00。剪脹角對計算結果的影響不大,剪脹角取值范圍是3°~16.5°。采用7因素28水平的均勻試驗劃分,因素選擇為重度、變形模量、黏聚力、內摩擦角、水平側壓力系數、泊松比、剪脹角7個因素,應用均勻試驗法設計28個數值試驗方案,采用 FLAC3D 軟件進行三口隧道左線施工的三維數值模擬,考慮不同的掌子面與 ZK252+510 監測面的距離,從數值實驗的結果中隨機抽取35次數值計算結果,組成供MSVR 算法進行網絡訓練的 30個訓練樣本見表6,5個檢驗樣本見表7。訓練樣本采用K折交叉驗證法進行MSVR模型的學習及建立。表7所示的檢驗樣本完全不參與MSVR模型的訓練過程,只用來檢驗訓練得到的MSVR模型的泛化性能。MSVR采用徑向基核函數,并對樣本進行歸一化處理,將數據線性映射到[0,1]。將拱頂下沉和水平收斂作為MSVR模型的輸出變量建立MSVR模型,對模型參數(C,ε,σ)進行優化。三個參數的搜索區間依次為(0,10 000)、(0,100)、(0,10 000),經過ICSA算法優化后,MSVR模型最優參數C,ε,σ的數值分別為19.4、0.004 59、2.10。 表6 MSVR模型訓練樣本集 表7 檢驗MSVR訓練效果的檢驗樣本集 為檢驗模型泛化性能,對表7所示檢驗樣本,用訓練好的MSVR模型進行位移預測,結果見表8。 表8 檢驗樣本的MSVR模型預測效果 由表8可知,MSVR模型對于拱頂下沉和水平收斂的預測精度較好,表明映射圍巖物理力學參數與位移之間非線性關系的MSVR模型已經建立,可以用于巖體物理力學參數的辨識。 利用訓練完成的MSVR模型,對巖體物理力學參數進行反演,7個待反演參數的反演區間見表9。將拱頂沉降和水平收斂統一反演,兩者權重相等,反演目標函數見式(17),取監測面距離掌子面5 m處時的位移值作為反演基礎信息。反演得到的巖體物理力學參數見表9。 表9 待反演、反演參數取值范圍 利用反演得到的巖體力學參數,輸入MSVR模型對后續位移(d=8、11、14 m)進行預測,預測效果見表10。由表10可知,利用ICSA-MSVR算法對隧道進行位移反分析,其后續位移預測中,拱頂下沉和水平收斂的預測具有較好的精度,誤差最大在15%左右,說明基于免疫多輸出支持向量回歸算法的位移反分析方法具有較高的精度。 表10 反演參數預測后續位移 為進一步說明本文所述ICSA-MSVR算法對位移反分析問題的求解效果,與文獻[7]中方法進行對比,文獻[7]中采用遺傳-廣義回歸神經元網絡算法(GRNN)對塢石隧道進行位移反分析,基于塢石隧道的實測位移值,對隧道圍巖的物理力學參數進行辨識。文獻[7]采用數值試驗、機器學習與人工智能相結合的智能巖土工程反分析方法,與本文具有可對比性。 根據文獻[7]中表6所述的隧道實際監測位移,可以確定如式(17)所示的反演目標函數,按照本節所示工程實例的相同步驟,對塢石隧道的圍巖參數進行辨識,本文方法和文獻[7]方法反分析得到的圍巖力學參數對比見表11。 表11 反演參數對比 將反演得到的巖土參數輸入到MSVR模型,進行后續的開挖步的隧道變形的預測,對比結果見表12。由表12可知,本文ICSA-MSVR算法對隧道變形的預測精度高于單一的BP方法,與遺傳-廣義回歸神經元網絡算法(GRNN)對比,精度略有提高,本文方法對拱頂沉降和水平收斂的統一反演效果較好。也體現出多輸出支持向量回歸算法與免疫克隆選擇算法相結合的良好的位移反分析應用前景。 表12 位移預測結果對比 本文所述算法,均編制C++程序,并借助Intel OpenMP并行算法庫實現了算法的并行,提高其計算效率。算法計算時間見表13。 表13 算法花費時間表 s (1) 本文提出了改進的免疫克隆選擇算法,加入了種群抑制過程來改善收斂于局部極值以及算法的早熟問題,經過算例檢驗,該算法對多維優化問題具有良好的求解能力,且收斂速度較快。 (2) 引入多輸出的支持向量回歸算法,用來解決輸出變量之間的依賴性以及計算效率的問題,增強了位移反分析方法的工程應用價值。 (3) 將本文方法應用于銅黃高速公路三口隧道的位移反分析中,結果顯示本文方法的參數辨識效果較好,辨識的參數較為準確,對后續位移的預測精度較好,具有一定的工程應用價值。并將本文所述ICSA-MSVR算法與遺傳-廣義回歸神經元網絡算法進行了參數辨識的對比,驗證了本文方法的優勢。2 免疫克隆選擇算法



3 基于ICSA-MSVR耦合算法的巖體物理力學參數位移反分析

4 工程實例
4.1 三口隧道工程概況
4.2 訓練樣本的獲取——數值試驗
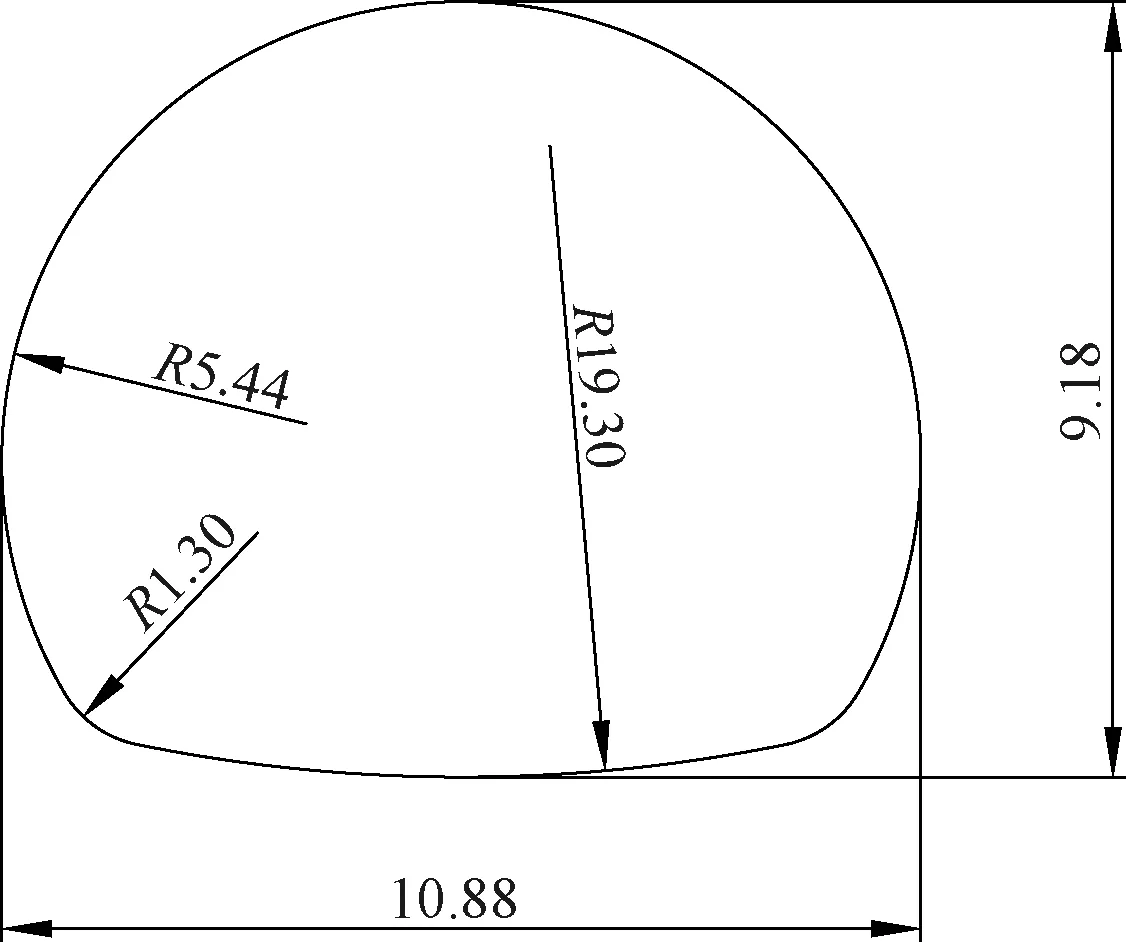


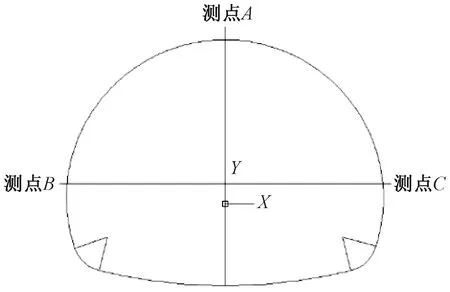




4.3 巖體參數的反演及后續位移預測





5 結論

