隧道爆破振動信號畸變校正與混沌多重分形特征研究

付曉強， 俞 縉， 劉紀峰， 楊仁樹， 戴良玉

(1. 三明學院 建筑工程學院，福建 三明 365004；2. 華僑大學 福建省隧道與城市地下空間工程技術研究中心，福建 廈門 361021；3. 三明科飛產氣新材料股份有限公司，福建 三明 365500； 4. 北京科技大學 土木與資源工程學院，北京 100083)

隧道鉆爆法過程中，不可避免會對周圍環境產生負面影響，爆破振動監測作為爆破損傷評估、孔網參數調整優化的重要依據，對指導工程施工具有積極的現實意義[1-2]。目前，隧道開挖仍普遍采用毫秒雷管進行振動控制，鑒于普通雷管起爆精度的不確定性和爆破振動控制的不穩定性，通過定性和直觀分析無法準確對爆破效果進行科學評價，信號的深入分析成為必然趨勢。由于測試環境復雜性和儀器本身的原因，監測信號中均不同程度含有干擾成分，如噪聲、趨勢項等，上述不相干分量在信號預處理過程中必須準確辨識并有效分離，才能消除其對信號真實信息的干擾，這也是現階段信號處理的關鍵問題。如王海龍等[3]對隧道爆破信號中的噪聲特征進行了分析，提出了適合隧道爆破信號去噪組合方法；賈貝等[4]針對經典模態分解方法的缺陷，采用變分模態分解方法對隧道爆破信號趨勢項進行了消除，并對相關影響因素進行了分析；張勝等[5]通過構造自適應小波基有效去除了奇異信號中包含的趨勢項，后續能量分析過程也驗證了算法的精度；Liu等[6]采用小波閾值方法對不同裝藥結構爆破信號進行了分析，提取得到不同結構下的信號特征。上述算法在爆破信號處理方面均顯現出獨特的優勢，但對于噪聲和趨勢項同步聯合處理分析還未見廣泛報道。

近年來，爆破信號非線性特征亦為研究分析的熱點。非線性特征蘊含著反映爆破本質和破巖機理的重要信息，如時頻域、能量熵、分形和混沌特性等，如Zhao等[7]采用時頻分析方法分析了爆心距對信號頻譜特征的影響，細化了爆心距對信號特征的關鍵作用；趙明生等[8]采用二次型平滑偽魏格納-維爾分布算法對不同微差間隔下的單段疊加信號的振速峰值和主頻特征進行分析，提出了將能量作為建(構)筑物損傷影響的量化參數；單仁亮等[9-10]采用小波包方法對隧道和立井模型試驗監測信號進行了能量特征提取，總結得到了爆破能量衰減規律，為類似工程爆破安全評估提供依據；鐘明壽等[11]基于多重分形理論對碳酸鹽巖爆破地震波的分形行為進行了研究，精確描述了爆破信號的局部奇異性和分形特征；付曉強等[12]運用混沌理論揭示了凍結立井爆破信號不同頻帶子信號的混沌吸引子形態特征，研究結果表明混沌吸引子形態變化可作為信號主頻判別和能量表征的指標。

本文依托青島地鐵3#線隧道掘進工程，對隧道掘進爆破振動進行了有效監測。采用稀疏化基線估計與去噪(baseline estimation and denoising with sparsity，BEADS)算法實現了信號趨勢項、噪聲和真實信號的分離，利用多重分形去趨勢波動分析(multi-fractal detrended fluctuation analysis，MF-DFA)方法分析了信號不同分量的多重分形和混沌特征，并基于交叉小波變換對不同成分信號的時頻相關性進行了分析，深刻揭示了爆破信號的非線性行為特征，為信號不同成分的有效辨識和特征分類提供了探索性思路。

1 基本算法

1.1 BEADS算法

將復雜信號分解為簡單分量的線性組合是信號分析的重要途徑。稀疏分解理論認為，信號分解結果越稀疏則越接近信號的本征或內在結構，信號稀疏表示可有效揭示非平穩信號的時頻結構[13]。對于任意稀疏化信號s(t)，若其中含有N點隨機成分，則該信號可表示為本征分量與緩變漂移信號的組合，即

s(t)=x(t)+f(t)，s(t)∈RN

(1)

式中：x(t)為包含無數峰值的稀疏可微本征信號成分；f(t)為信號中含有的緩變基線偏移成分，其為低通分量。受外界環境影響，測試信號中通常亦會含有一定的隨機噪聲。因此，可將受基線偏移和噪聲影響的信號y(t)進一步表示為

y(t)=s(t)+w(t)=x(t)+f(t)+w(t)，y(t)∈RN

(2)

式中，w(t)為奇異信號中含有的隨機干擾噪聲。上述分量信號的有效分離依賴于相關參數的精確選取，如截止頻率fc，其決定了基線分量與剩余分量信號之間的界限；不對稱系數r，用于補償運算過程中產生的頻譜負值；正則化參數λ(λ0～λ2)，可控制分解信號x(t)的稀疏性。另外一個重要的參數為幅值A，其乘以正則化參數(A×λi)便可使得λi選取與信號幅值無關。

基線成分為信號中緩慢變化的趨勢分量，為信號漂移、儀器漂零或測試環境引起的偏差，通過建立低通濾波器提取；白噪聲為信號中包含的高頻噪聲，通過建立高通濾波器獲取；將上述兩個分量從初始信號中剔除，便得到了能夠反映信號信息特征的真實信號。

1.2 MF-DFA算法

多重分形去趨勢波動分析方法是在傳統波動去趨勢項分析(detrended fluctuation analysis，DFA)方法的基礎上改進而提出的，其能夠有效揭示爆破振動等這類非線性、非平穩信號的動力學行為[14-15]。相較與傳統的多重分形算法，其核心優勢主要有：①充分利用信號序列數據長度，正反雙向對信號序列進行等時間長度劃分；②通過最小二乘法對各個分段進行多項式擬合，消除數據序列中非平穩趨勢的影響；③利用不同階次波動函數分析時間序列在不同層次上的標度行為，精細刻畫數據序列的分形特征，揭示隱藏在非平穩時間序列的多重分形特征。

對于長度為N的爆破振動信號時間序列{x(k),k=1,2,…,N}，MF-DFA求解過程如下。

計算{x(k)}偏離均值的累計離差y(i)

(3)

將y(i)劃分為Ns個等長度s的小區間序列，即

Ns=int(N/s)

(4)

由于在劃分過程中N未必恰好是s的整數倍，則必定會存在除不盡的余值。為了保證數據序列不丟失信息，將這部分余值保留并從y(i)尾部開始，逆向重復上述劃分過程，便會得到2Ns個子序列。

利用最小二乘法擬合各個子序列的局部趨勢函數yv(i)為

yv(i)=a0+a1i+a2i2+…+akik

(5)

式中：ai為擬合多項式的系數，i=0,1,…,k；k為多項式擬合最高階數。

對于奇異爆破信號，“趨勢項”的消除是通過離差y(i)減去擬合局部趨勢函數yv(i)來實現的，因此不同擬合階數i可體現“趨勢項”被消除的程度。

(6)

確定q階波動函數Fq(s)

(7)

式中，階數q的取值為非零實數。特別地，當q取值為2時則退化為標準的DFA法。若序列{x(k)}存在自相似特征，則其具有多重分形特征。則q階波動函數Fq(s)與s之間存在冪律關系[16]

Fq(s)～sh(q)

(8)

式中，h(q)為廣義Hurst指數，表征原始序列的相關性，h(q)大小取決于q值的變化。當信號{x(k)}為單分形時間序列，則F2(s,v)在所有小區間標度是恒定值，此時h(q)為與q值無關的常數。

1.3 MF-DFA和經典多重分形理論關系

通過MF-DFA方法得到的h(q)和經典多重分形算法中由標準配分函數得到的標度指數τ(q)存在如下關系[17]

τ(q)=qh(q)-1

(9)

結合Legendre變換對式(9)等號兩邊對q求導便得到多重分形譜f(a)，奇異指數α和τ(q)三者之間滿足關系

(10)

2 隧道爆破信號零偏校正

青島地鐵3#線隧道全長25.93 km，采用鉆爆法施工。開挖斷面為馬蹄形，掘進斷面積為30.8 m2，寬度為5.8 m，高度為6.1 m。隧道爆破選用共7個段別電雷管，分別為MS1～MS13跳段使用，可以最大程度降低爆破產生的振動效應。選用2#巖石乳化炸藥，布置掏槽孔24個，分別采用MS1、MS3、MS5三段起爆，對應的各段別起爆藥量為7.2 kg、7.2 kg和10.8 kg；輔助孔40個，分別為MS5、MS7、MS9三段起爆，各段別起爆藥量分別為1.8 kg、10.2 kg和12 kg；周邊眼30個，為MS11段起爆，起爆藥量為13.5 kg；底眼7個，為MS13段起爆，起爆藥量為4.2 kg。單循環總裝藥量為66.9 kg，具體炮眼布置如圖1所示。

圖1 爆破孔網參數(mm)

為了準確評估和反映隧道爆破產生的振動效應，在隧道開挖掌子面上方22 m處布置測點。測試采用TC-4850型爆破測振儀，測振儀參數的準確設定是保證爆破信號測試精度的前提條件。為了保證測試波形的完整性及滿足Heisenberg測不準原理的要求，將采樣頻率設定為8 kHz，采樣時長為2 s。測振儀具體測試分析流程如圖2所示。

圖2 TC-4850測試及分析流程

測試時建立笛卡爾坐標系，將測振傳感器水平x向(徑向)指向隧道掘進軸線方向，y向(切向)指向與軸線垂直的水平方向，z向(垂向)指向與xy所構成平面垂直的豎向,從而獲取相互垂直的三個方向上的振動信息。測振儀監測到的典型畸變振速波形如圖3所示。

圖3 隧道爆破振動信號波形曲線

三向振速波形出現顯著差異，其中與隧道軸線平行的x向振速最大，y向次之，z向最小。與常規露天爆破等多自由面爆破不同，隧道爆破掘進自由面單一，巖石夾制力較大，導致在裝藥量較小的低段別產生強振，伴隨后續段別的順利起爆，瞬間形成第二附加自由面，振速幅值有所降低；另一方面，雷管段別越高，雷管誤差相對也越大，這也解釋了該隧道微差起爆周邊眼的MS11段總裝藥量大反而產生的振動卻較小的原因。高段別雷管誤差范圍相對較大，再加上炮孔數量較多，一定程度上形成了獨立的小型微差起爆網路，避免了周邊眼各炮孔瞬時起爆產生的振速峰值“疊加效應”。從圖3可知：隧道爆破振動主振波形持續時間主要位于0～1 s內，在0.8 s后逐漸衰減直至基線零點附近，符合爆破方案中雷管起爆及延期誤差時程分布區間規定(MS13段雷管起爆時刻標定值為：650 mm，下限為600 mm，上限為705 mm)。同時應注意到，三向振速波形曲線均存在一定的基線偏移現象，尤其以z向最為顯著，因此選取z向信號進行分析，其波形局部特征如圖4所示。z向信號在振動起始端部產生明顯的零漂，而在主振時程后具有明顯的“甩尾”趨勢項。引起這種現象的原因是多方面的，如儀器標定問題、爆破飛石、測試環境和測點布置等，若后續分析中將這類信號直接舍棄，會導致測試數據不完整，數據信息丟失甚至影響后期相關結論的科學性。因此，如何提高這類信號的可讀性和辨識度，是目前技術人員面臨的關鍵問題。

圖4 隧道爆破振動信號(z向)

信號分析過程中往往需要輸入多個相關參數，以確保得到的真實信號具有明確的物理意義。采用BEADS算法對信號進行處理時，所選截止頻率的微小變化會引起基線成分的較大波動，尤其在低于最佳頻率的中心頻率處體現的更為明顯，此外，高于最佳頻率的截止頻率會使基線成分對信號峰值極為敏感。考慮到基線成分主要集中在信號低頻區域，故設定分析截止頻率fc為0.002 Hz。

在分析過程中為了降低基線校正過程對信號分量幅值的影響，引入正則化系數λ和具有非對稱補償罰值功能的對稱損失函數φ。為了從y中提取x，問題轉化為下述優化問題，也稱為基追蹤去噪(basic pursuit denoising，BPD)過程

(11)

(12)

式中：φ:R→R為罰函數；參數λ決定了該過程中信號稀疏化程度。由于基線成分主要位于信號低頻分量中，分析時設置濾波器階數d取為0～2，損失函數非對稱性系數r取為6。正則化參數基本幅值λ為0.8，不同階正則化參數λ0～λ2分別為：0.8、3.2和4.0。分析過程中干擾因素很大程度上可通過調整非對稱系數r和正則化參數λ實現，信號分解提取結果及對應的信號頻譜，如圖5、圖6所示。BEADS算法通過建立凸優化問題來封裝上述分析過程中的非參數模型，引入類似正則化1范數的非對稱損失函數，是一種具有魯棒性、高效性且能快速收斂至最優唯一解的迭代算法。圖7中損失函數值與迭代次數歷史關系曲線表明，經過有限次數(<15次)的迭代損失函數值便趨于收斂，驗證了算法運行效率。

圖5 信號BEADS分析結果

圖6 信號不同成分功率譜密度

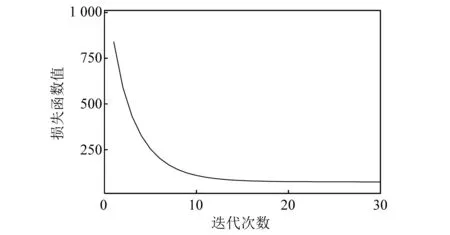
圖7 損失函數迭代歷時曲線

3 混沌多重分形特征分析

3.1 混沌特征

隧道微差起爆網路可視為復雜的非線性動力系統，爆破信號的非線性動力學特征具有對網路裝藥量、雷管段別選取等初始條件的敏感依賴性、起爆過程延期時間的不確定性以及能量時空分布的隨機性。信號混沌運動軌跡稱為混沌吸引子，混沌吸引子上的混沌行為是一種高級有序行為。為了便于觀察不同分量信號相空間軌跡演化規律，將信號根據時間分成若干段，重構后投影到三維相空間中，繪制其吸引子演化過程，具體過程詳見付曉強等[18-19]的研究。不同分量信號吸引子形態在三維相空間軌道的精細程度、相空間軌跡的收斂程度、信號不同成分所蘊含的信息量以及穩定程度具有顯著差異，如圖8所示。校正信號波形穩定規則，吸引子在相空間軌跡為長軸、短軸不等長的橢圓形平衡態，其在軌道之間表現為由密到疏的反復周期性波動過程，體現了微差爆破過程中低段別起爆能量的不斷耗散和高段別起爆能量的相繼補充作用；低頻趨勢項成分能量較小，吸引子在三維相空間收斂為近似直線，揭示了趨勢項為大波動的長周期干擾特征；高頻噪聲振幅明顯減小，吸引子在相空間周期性成分減弱，呈現為無明顯軌道的雜亂無章狀態，說明了噪聲成分具有微幅隨機性波動特征。

圖8 爆破信號不同成分混沌吸引子形態演化

針對非線性信號特征的分析，Eckmann等提出了一種圖形化的信號提取方法，即遞歸圖(recurrence plot，RP)理論。遞歸圖是一種能夠深刻揭示信號不平穩并識別標量時間序列中隱含規律的圖形方法，其從宏觀角度分為均勻模式、周期模式、漂移模式和突變模式[20-21]。這里，分別計算三個分量信號的遞歸圖，如圖9所示。圖9中不同分量信號遞歸圖模式特征明顯不同，遞歸拓撲結構清晰可辨。校正信號的遞歸圖在時間軸上表現為周期模式，屬于典型的穩態分布，局部密度增大與信號波峰、波谷出現位置密切相關，具有強烈的非線性特征；低頻趨勢項成分的遞歸圖呈對角線方向分布，分布走向大致平行于45°主對角線方向，表現為突變模式且對角線和孤立點并存，說明趨勢項屬于信號中的緩慢變化成分，其線性程度增強；而噪聲成分遞歸孤立點隨機分布，表現為漂移模式，表明高頻低幅噪聲引起的干擾由信號中突然的或急劇變化所決定。遞歸模式和混沌特征為爆破信號不同成分的辨識提供了理論依據和參考。

圖9 爆破信號不同成分遞歸圖演化

3.2 多重分形特征

應用MF-DFA對圖5中隧道爆破信號不同分量進行分析，將尺度s區間取為16～1 024并等間隔劃分，共得到19個尺度值范圍內的信號波動特性。計算時k值確定為2，取階數q分別為-1,0,1，便得到校正信號、趨勢項和噪聲三個特征信號的雙對數回歸曲線，如圖10所示。

圖10 尺度函數波動雙對數回歸曲線

圖10信號不同成分波動函數與尺度雙對數擬合關系中，波動函數F(q)均隨著尺度s的的變大而增大，F(q)對尺度s的對數回歸線的斜率即為Hurst指數。圖10中不同信號在尺度s變化下的波動趨于一致，隨著尺度s的增加，波動聚集性增強，F(q)值差異性降低。校正信號的波動趨勢更為明顯，體現了不同段別雷管起爆能量對信號總能量的補充過程，其頻率成分相對復雜，具有典型的瞬態非線性大波動特征；趨勢項信號呈現近似線性的波動狀態，體現了趨勢項的小波動形態；噪聲信號在大、小不同尺度s下的波動性態無明顯差異，反映了噪聲信號弱波動行為。

Hurst指數h(q)反映了信號不同階數q之間的關系，是衡量信號多重分形特性的重要指標。計算爆破信號三種成分在不同階數q下的Hurst指數值，如表1所示。從表1可知，爆破信號中不同成分的Hurst指數均隨著q值增大而減小，體現了不同信號成分分形特征差異。

表1 爆破信號不同分量的Hurst指數

校正信號、趨勢項和噪聲在不同階數下的Hurst指數呈現漸進式遞減變化。通常Hurst指數取值介于[0,1]，h(q)值的變化可體現爆破信號的持續相關性。從表1可知：噪聲成分00條件下為反持續相關性。三類信號Hurst指數變化具有清晰的辨識度，可作為信號辨識和分類的依據。

三種信號成分的多重分形譜及相關參數變化，如圖11所示。圖11(a)校正信號在幅值上介于低頻趨勢項和高頻噪聲之間，體現了校正信號寬頻分布特征。圖11(b)三者中趨勢項的非線性特征最強，噪聲最弱，校正信號居中，反映了校正信號多幅值屬性。圖11(c)表現出校正信號和趨勢項分形譜對階數q變化較為敏感，噪聲卻相反，這與表1得到的結論一致。圖11(d)校正信號、趨勢項及噪聲信號標度指數τq與q均為非線性關系且校正信號非線性程度介于低頻趨勢項和高頻噪聲之間，在階數q=0時三者標度指數值接近并趨于一致。階數為負值時，標度指數能敏感地捕捉信號不同成分小幅值變化，反之，則能敏感反映其大幅值變化。可以看出無論哪類信號成分，q=0時，τq=-1，τq是一個凸向縱軸的函數，τq與q之間存在非線性關系且隨著信號頻率的增大非線性程度降低。

圖11 爆破信號不同成分MF-DFA分析結果

圖11(e)中奇異譜f(α)是奇異指數α的分維分布函數。多重分形譜f(α)有三個特征點，即左、右端點和極值點。多重分形奇異譜曲線在左端點的斜率q→+∞，因此左端點的橫坐標α+∞對應著最大波動的奇異指數；在右端點處斜率q→-∞，因此，右端點的橫坐標α-∞對應著最小波動的奇異指數。多重分形譜的寬度Δα=α-∞-α+∞反映了時間序列在整個分形結構上概率測度分布的不均勻性程度，Δα越大則概率測度分布越不均勻，多重分形越強烈。三種信號成分的多重分形譜及相關參數提取結果，如表2所示。

表2 信號MF-DFA分形譜參數

三類信號的奇異譜具有不同的形狀、位置和譜寬，均為類似“鐘形”曲線，表現為單峰拱形且峰值均為1，這是多重分形譜的一個重要特征。三種信號多重分形譜都是以α值的某個范圍為特征，分形譜對應的奇異指數α隨著信號頻率的增大而逐漸左移；校正信號和趨勢項Δf均為正值，噪聲信號為負值。爆破信號不同成分奇異譜沿峰值點近似軸對稱分布且校正信號的多重分形強度最大，趨勢項次之，噪聲信號最小。正是由于三類信號內在動力學機制不同，產生了上述譜差異。

4 信號相關性分析

對于任意給定的兩個信號x(t)和y(t)，在其連續小波變換的基礎上建立兩者之間的相關性關系[22]

(13)

上述系數值變化可揭示信號在時頻域不同尺度上的相關程度，其值越大則相關性越高，反之亦然。小波相關性凝聚譜綜合反映了不同信號之間的相關性在時域和頻域上的依賴關系，揭示不同信號成分與原始信號在時間和頻率尺度上的相關程度。分析過程中，選用Morlet小波基函數可獲得良好的時頻域局部化特征，這里為了便于分析，對相關性進行歸一化處理，如圖12中顏色柱所示。圖12中黑色小箭頭代表被分析信號間的位相關系，箭頭向右(→)表示兩信號之間為同位相，為顯著正相關；箭頭向左(←)表示兩者之間為反相位，呈現顯著負相關關系；箭頭垂直向上或向下(↑或↓)表示位相出現滯后性，為非線性相關。由相關性對比可知：校正信號與原始信號在全時程和特征頻段(16～128 Hz)內表現出強烈的同位相相關性。基線信號與原始信號僅在主振時程0.7 s內存在一定的反位相趨勢，且相關性出現間斷不連續特征。噪聲信號與原始信號在時頻域上的依賴性顯著降低，幾乎無關聯性。分析實踐也表明如果截止頻率選取合理，從原始奇異信號中將校正信號和基線信號成分去除得到的殘余噪聲理論上其與原始奇異信號無相關性。交叉小波凝聚譜清晰刻畫了信號不同分量對原始信號特征的繼承性，為三類信號的辨識提供了客觀依據。

圖12 不同信號成分與原始信號相關性凝聚譜

5 結 論

針對隧道爆破振動信號趨勢項和噪聲干擾識別難題，采用組合算法分離并提取信號的混沌分形特征，結論如下：

(1) BEADS算法可實現爆破校正信號、低頻趨勢項和高頻噪聲的有效分離，三者均具有多重分形特征且噪聲具有絕對的反持續相關性，體現了其成分的波動離散性；趨勢項具有持續相關性，持續性強弱與階數q值大小為負相關，階數q值越小，持續性特征越顯著；校正信號以階數q=0為轉折點，在q<0條件下表現為持續相關性，而在q>0條件下為反持續相關性。

(2) 高頻噪聲、低頻趨勢項和校正信號三者的混沌特征顯著不同。校正信號吸引子軌跡形態為反復周期性有序波動，其遞歸圖具有周期模式；趨勢項吸引子表現為近似直線，其遞歸圖具有對角線分布突變模式；噪聲吸引子為雜亂無章隨機波動，其遞歸圖具有漂移模式。

(3) 交叉小波變換凝聚譜可揭示信號在時域和頻域變化的細部特征和共振位相差異，反映信號不同成分在時頻域特征的相關程度，校正信號、趨勢項和噪聲分量與原始信號分別具有持續正相關、局部負相關和無相關性特征，為三類信號的分類識別和特征信息繼承度判定提供了有效手段。