古箏弦-碼結(jié)構(gòu)的三維動力學(xué)分析與試驗驗證

鄧小偉， 余征躍， 姚衛(wèi)平， 周 力

(1. 上海交通大學(xué) 船舶海洋與建筑工程學(xué)院，上海 200240； 2. 上海民族樂器一廠，上海 201101)

古箏是中國獨特的、重要的民族樂器之一。它的音色優(yōu)美、音域?qū)拸V、演奏技巧豐富，具有相當(dāng)強(qiáng)的表現(xiàn)力，因此深受廣大人民群眾的喜愛。同時它也承載了傳播中國民族文化的重任[1]。隨著當(dāng)今科技的迅猛發(fā)展，西方樂器在制作規(guī)范、聲音品質(zhì)控制以及穩(wěn)定性等方面都非常成熟，而我國民族樂器古箏由于相關(guān)理論研究的缺乏，目前整體相對落后，主要表現(xiàn)在：結(jié)構(gòu)設(shè)計缺少科學(xué)指導(dǎo)，結(jié)構(gòu)不穩(wěn)定；制作方式和手段相對傳統(tǒng)、落后，制琴質(zhì)量無法保證[2-4]。因此對于民族樂器古箏的理論研究顯得尤為重要[5-8]。

古箏的弦-碼結(jié)構(gòu)是其演奏發(fā)聲過程中的主要振動及傳導(dǎo)系統(tǒng)，同時也是影響古箏發(fā)聲特性的最主要部分[9]。為此對古箏弦-碼結(jié)構(gòu)振動特性的研究是了解古箏發(fā)聲原理并為其結(jié)構(gòu)聲學(xué)設(shè)計提供理論依據(jù)的關(guān)鍵性工作。總結(jié)相關(guān)樂器的弦振動研究，楊健[10]回顧了琴弦研究的發(fā)展，討論了達(dá)朗貝爾的弦振動方程，用理想撥弦模型分析了撥弦振動的軌跡、觸弦點對音色和音量的影響等；李云芳[11]利用弦振動的基本方程推導(dǎo)分析了使用平面錘、凸面錘和細(xì)棒敲擊揚琴弦時的振動方程，通過分析n次諧波衰減的快慢，得出不可使用細(xì)棒；Mandal等[12]對考慮柔性音板下的弦-板協(xié)調(diào)振動特性進(jìn)行研究，給出了板厚、位置、質(zhì)量等對弦-板振動特性的影響，并給出了最佳參數(shù)選擇；Taguti[13]利用弦振動方程建立sawari的弦振動模型，分析了弦端在振動中觸弦點變化致使發(fā)出獨特音色的理論依據(jù)。這些研究都體現(xiàn)了弦振動特性對樂器聲音表現(xiàn)的重要作用，但目前針對古箏這類以弦-碼結(jié)構(gòu)作為振動傳導(dǎo)系統(tǒng)的樂器，對其相關(guān)振動特性的研究相對缺乏。文獻(xiàn)[14]將古箏的弦-碼結(jié)構(gòu)簡化為平面問題，初步建立了古箏弦振動通過琴碼傳遞到面板的動力學(xué)模型，并進(jìn)行數(shù)值計算和試驗驗證，很好的解決了古箏聲振特性研究中弦-碼結(jié)構(gòu)的理論模型建立問題。然而將其簡化為平面問題，就無法體現(xiàn)古箏琴碼雙碼腳設(shè)計對古箏聲振特性的影響及古箏演奏過程中不同撥弦方式對古箏發(fā)聲的影響[15-16]。為此在考慮古箏琴碼雙碼腳的情況下建立古箏弦-碼結(jié)構(gòu)的三維動力學(xué)模型，并分析不同撥弦角度時各碼腳法向作用力的變化規(guī)律及對古箏發(fā)聲的影響顯得十分必要。

綜上所述，本文首先研究了古箏琴弦的振動，并建立弦振動的動力學(xué)模型；在此基礎(chǔ)上建立古箏弦-碼結(jié)構(gòu)的三維動力學(xué)模型，并根據(jù)不同的演奏撥弦方式，利用MATLAB軟件數(shù)值計算了不同撥弦角度下琴碼各碼腳的法向作用力，并進(jìn)行試驗驗證；最后根據(jù)數(shù)值計算以及試驗測量結(jié)果分析了各碼腳作用力的變化規(guī)律以及對古箏發(fā)聲的影響。

1 古箏弦振動的簡化模型

古箏的琴弦是兩端固定，中間利用琴碼頂在古箏面板上的，演奏者通常以撥弦的方式讓琴弦獲得初始狀態(tài)后自由振動。雖然琴碼在弦振動的過程中會有位移，但通常相對弦的振動幅度屬于微小位移，琴碼可視為固定，可將其弦振動簡化為有界弦的振動[17-18]。

設(shè)琴弦的有效弦長為L，以弦的左端固定點為原點，琴碼端為終點，建立空間直角坐標(biāo)系，弦長方向為x軸，垂直于弦長且平行于面板的方向為y軸，垂直于弦長且垂直于y軸的方向為z軸，弦的橫向振動方向為u軸，彈撥點在x=x0處，簡化模型如圖1所示。

圖1 古箏弦振動簡化模型

古箏演奏中所用到的彈奏指法變化很多，其中最常用到的包括托、勾、抹、打等指法，這些演奏指法都是在彈撥琴弦的過程中給與弦初始狀態(tài)后讓其自由振動，但指法的不同也會致使弦的振動方向不同。以托、勾等指法為例，一般給與弦初始位移且施力方向為水平或向上，為此這里假設(shè)撥弦的方向為u軸方向，忽略撥弦“義甲”的寬度，則整個弦的初始位移在x軸方向成線性變化。設(shè)彈撥處弦的初始位移為u0，之后弦開始自由振動，則撥弦的振動可歸結(jié)為定解問題[19]

(1)

式中：a2=T/ρ，T為弦張力；ρ為弦的線密度。

利用分離變量法，以傅里葉級數(shù)表達(dá)其定解為

(2)

其中

(3)

(4)

將式(3)、式(4)代入定解式(2)得

(5)

式(5)為撥弦的振動方程，其中n為正整數(shù)，n=1的部分為基波，其他每一個n代表一個諧波成分。

2 古箏弦-碼結(jié)構(gòu)的動力學(xué)建模分析

古箏演奏中弦-碼的聲學(xué)機(jī)理是利用義甲的彈撥使琴弦獲得初始狀態(tài)后自由振動，再通過琴碼將琴弦的振動以力的形式傳遞到古箏面板。其傳遞過程主要是弦振動時琴弦的形態(tài)改變，使弦張力以及琴弦與碼的夾角產(chǎn)生變化，使得通過琴碼向下傳遞到面板的力不斷改變，使古箏結(jié)構(gòu)做強(qiáng)迫振動，從而發(fā)聲[20-21]。

假設(shè)琴弦的有效振動弦長為L，琴碼的作用高度為h，琴弦振動時弦張力為時變函數(shù)TL(t)，而琴弦給琴碼向下的合力為時變函數(shù)F(t)，給琴碼的側(cè)向作用力為時變函數(shù)Fy(t)，弦振動的方向u軸垂直與弦長方向x軸，即在yz平面內(nèi)，琴碼兩個碼腳給面板的傳遞作用力分別為時變函數(shù)f1(t)、f2(t)，琴碼在傳遞作用時的位移忽略不計，只考慮力的作用，琴碼右邊的按弦部分作用也忽略，可得到琴碼傳遞的簡化模型如圖2所示。

圖2 古箏琴碼傳遞簡化模型

從圖2可知，進(jìn)行受力分析琴弦張力為

(6)

式中：A=πd2/4，d為裸弦直徑； Δl為弦振動時的形變量；E為弦芯鋼絲的彈性模量；T為靜態(tài)的弦張力。

根據(jù)撥弦時的弦振動方程式(5)分析弦的形變可知

(7)

其中

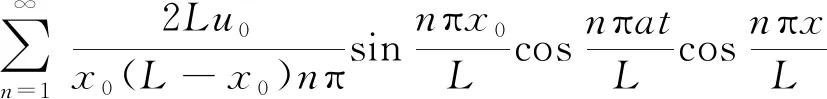
(8)

又由于u0相對于L為極小量，故

根據(jù)數(shù)學(xué)極限公式可得

(9)

將式(9)代入式(7)有

(10)

這里將弦的形變量表示為各階弦振動形變的疊加項Δls(t)與相互間的耦合項Δlc(t)之和。

(11)

(12)

分析琴弦與琴碼的位置關(guān)系和受力情況，得到其左半弦(振動部分)簡化模型，如圖3所示。圖3中琴碼的作用高度(即琴碼端擱弦點相對岳山端擱弦點的垂直高度)為h，而琴碼的實際高度為H，琴碼的兩碼腳間距為b，弦長方向與面板的夾角為α，弦振動過程中TL(t)與x軸的夾角為時變函數(shù)β(t)，弦振動方向u軸與y軸的夾角為γ。

圖3 古箏琴碼傳遞簡化模型

根據(jù)圖3對弦-碼結(jié)構(gòu)的受力分析，可知，TL(t)可分解為x軸和u軸的分量，分別為

Tx(t)=TL(t)cosβ

(13)

Tu(t)=TL(t)sinβ

(14)

由式(13)和式(14)所示的TL(t)分力，可知琴碼受到的作用力為

Fy(t)=Tu(t)cosγ

(15)

F(t)=Tx(t)sinα-Fz(t)cosα=Tx(t)sinα-Tu(t)sinγcosα

(16)

將琴碼單獨做受力分析，其正視圖如圖4所示。

根據(jù)圖4的受力分析可知

圖4 琴碼受力分析圖

f1(t)+f2(t)=F(t)

(17)

f1(t)·b/2=f2(t)·b/2+Fy(t)·H

(18)

將式(17)和式(18)聯(lián)立方程組求解可得

f1(t)=[F(t)+2Fy(t)H/b]/2

(19)

f2(t)=[F(t)-2Fy(t)H/b]/2

(20)

將式(13)～式(16)代入式(19)、式(20)可得

(21)

(22)

根據(jù)式(6)、式(8)、式(10)、式(11)、式(12)有

3 碼腳作用力的數(shù)值分析與試驗驗證

根據(jù)理論推導(dǎo)的古箏兩碼腳作用力公式，通過MATLAB軟件數(shù)值計算對其不同撥弦方式下碼腳作用力的變化規(guī)律進(jìn)行分析[22-23]，并通過試驗測量進(jìn)行對比驗證。以古箏的21號弦為例，經(jīng)過對上海民族樂器一廠生產(chǎn)的敦煌-698T傳統(tǒng)古箏的測量，得到其琴弦的有效弦長L=950 mm，有效內(nèi)徑d=0.61 mm，線密度ρ=20.57 g/m，彈性模量E=220 GPa，阻尼系數(shù)ξ=0.35，利用Tensometric-Combi-490張力測量儀測得琴弦張力T=480 N，彈撥位置取常用演奏位置x0=1/7L處，最大初始位移u0=3 mm，而琴碼的作用高度h=45 mm，琴碼的實際高度為H=60 mm，琴碼的兩碼腳間距為b=50 mm，弦振動方向u軸與y軸的夾角γ根據(jù)不同的撥弦方式，其分別取0°、45°、90°和135°。計算中取前10階即n=10，計算時長t=1 s，時間間隔為Δt=0.000 04 s。

古箏琴碼對面板作用力的測量。利用KD3001力傳感器粘貼在處理過的琴碼的左右碼腳上，并保證其整體高度與原琴碼一致，將傳感器連AVANT-MI-2004調(diào)理放大器，信號通過9234采集卡連接至計算機(jī)，并利用LabVIEW進(jìn)行試驗測量，測試框圖如圖5所示。其中KD3001力傳感器成圓環(huán)形，外徑為φ16 mm內(nèi)徑為φ5 mm，且底面為平面，其測量范圍在1～5 kN，自身固有頻率在70 kHz，使用頻率在20 kHz。

圖5 琴碼傳遞力測試框圖

試驗時，將弦的發(fā)音調(diào)至規(guī)定值，即21號弦所對應(yīng)音名D的頻率73.4 Hz，然后在弦1/7處沿y向(0°角方向)利用粘貼有應(yīng)變片的模擬義甲進(jìn)行撥弦，撥弦過程中實時監(jiān)測應(yīng)變片數(shù)值以確保撥弦初始位移的精確性和可重復(fù)性，同時記錄弦振動時琴碼左右碼腳力變化的數(shù)據(jù)。將測量結(jié)果按照左、右碼腳畫出各碼腳向下傳遞力試驗結(jié)果曲線，并與MATLAB軟件數(shù)值計算0°角的結(jié)果進(jìn)行對比驗證，同時根據(jù)時域曲線通過MATLAB軟件對其進(jìn)行快速傅里葉變換得到理論值和試驗值的頻譜曲線，如圖6所示。各撥弦角度MATLAB軟件數(shù)值計算結(jié)果左右碼腳的作用力時域曲線如圖7所示。

圖6 0°角撥弦琴碼向下傳遞力的理論值與試驗值曲線對比

圖7 各角度撥弦下左、右琴碼向下傳遞力的時域曲線

圖6描述的是0.1 s內(nèi)琴碼左右碼腳作用力理論值與實測值曲線的對比，從圖6可知，理論與實測曲線形狀相似，其中時域曲線上左碼腳理論值范圍為0～15 N，而實測值為0～17 N，右碼腳理論值范圍為8.0～22.5 N，實測值為6.0～22.5 N，理論值與實測值基本相近，其主要的峰值出現(xiàn)的時間差也相近。頻域曲線上左右碼腳理論與實測結(jié)果的幅值變化趨勢相似，其中理論值基本接近試驗值，第2階理論值小于試驗值，相對誤差較大，第7階的理論值與實測值都接近為0。前4階的具體數(shù)值對比和相對誤差，如表1所示。

表1 琴碼向下傳遞力理論值與試驗值對比

總體來說琴碼向下傳遞力的理論數(shù)值計算結(jié)果與實測值具有較好的一致性，考慮理論簡化以及數(shù)值計算和試驗測量的誤差，可見理論計算的結(jié)果基本可信，弦-碼結(jié)構(gòu)三維動力學(xué)模型可行。其中頻響結(jié)果中第2階相對誤差較大。原因與鄧小偉的研究相同，忽略了面板與琴弦、琴碼的耦合作用，因為在古箏結(jié)構(gòu)振動試驗中，古箏主結(jié)構(gòu)的2階固有頻率為138.13 Hz[24]，與21號弦的2階諧波頻率146.8 Hz接近，可見其耦合作用較大，為此進(jìn)一步工作中將著重解決其耦合效應(yīng)。圖7描述的是各撥弦角度琴碼左右碼腳作用力的時域曲線，結(jié)果顯示：水平撥弦時(0°角)，左碼腳動態(tài)力的最小值接近于0，說明該碼腳幾乎脫離琴體表面，可見水平撥弦易造成跳碼，與實際古箏演奏情況符合；豎直撥弦時(90°角)，左右碼腳的作用力同相位，且合力最大； 45°角撥弦與135°角撥弦琴碼作用力正好左右反對稱，且兩種撥弦方式左右碼腳的作用力相位相反。

4 結(jié) 論

通過簡化古箏琴碼為剛性雙碼腳，弦振動為有界弦振動，建立了弦-碼結(jié)構(gòu)的三維動力學(xué)模型，利用MATLAB軟件數(shù)值計算分析了不同撥弦角度時各碼腳法向作用力的變化規(guī)律，并進(jìn)行了試驗測量驗證。對比發(fā)現(xiàn)左右碼腳作用力的理論數(shù)值計算結(jié)果與實測值具有較好的一致性，考慮理論簡化以及數(shù)值計算和試驗測量的誤差，可見理論計算的結(jié)果可信，弦-碼結(jié)構(gòu)三維動力學(xué)模型可行；水平撥弦時，左碼腳動態(tài)力接近于0，可見水平撥弦易造成跳碼；豎直撥弦時，左右碼腳的作用力同相位，且合力最大； 45°角撥弦與135°角撥弦琴碼作用力反對稱，且兩種撥弦方式左右碼腳的作用力相位相反。