基于機器學習的山洪災害快速預報方法

周 聶，侯精明，陳光照，馬紅麗，洪增林，李新林

(1.西安理工大學省部共建西北旱區生態水利國家重點實驗室，陜西 西安 710048；2.鄂爾多斯市水利勘測設計院，內蒙古 鄂爾多斯 017000； 3.陜西省地質調查院，陜西 西安 710054)

山洪指在山區溪溝中由于強降雨等原因引起水位短時間內暴漲形成的洪水，具有流速大、沖刷力強、破壞力強等特點，通常會給交通、農業、居民生命財產安全等造成巨大威脅[1]。據《2017年中國生態環境狀況公報》統計，2017年洪澇災害累計受災人口5 515萬人，因災直接造成經濟損失達2 143億元[2]。隨著全球氣候變化，極端降雨事件頻率增大，2018年全國累計454條河流出現超過警戒水位的洪水，其中24條河流發生超歷史洪水[3]。由于山洪災害具有突發性及破壞性特點，如何應對山洪災害，降低損失，一直以來都是國內外學者研究的熱點與難點。

山洪災害模擬預報能夠有效模擬山洪災害的受災范圍，為山洪風險管理、應急決策提供依據，是協助防災減災工作的重要方式之一。眾多學者對此進行了研究，包紅軍等[4]基于新安江模型開發了分布式混合水文模型，模型預報精度較高；胡國華等[5]用HEC-HMS半分布式水文模型進行山洪模擬，洪峰流量及洪量相對誤差可控制在20%以內；孟天翔[6]基于MIKE FLOOD構建水動力模型開展山洪數值模擬，獲得各類洪水淹沒演進變化情況。然而傳統山洪模擬研究都有一個共同的缺陷，即需要求解復雜的方程組，按步時順序迭代以獲取洪水的演進過程，模擬運算耗時長，無法滿足緊急決策的需求。近年來，隨著人工智能技術的發展，機器學習技術以其普適性與高效性，在醫學、化學、數據挖掘等領域都得到了廣泛應用并展現出突出優勢[7-9]，國內外學者也逐漸將人工神經網絡、邏輯回歸、極限樹回歸等機器學習算法應用于洪澇災害的預測中[10-12]。闞光遠等[13]將ANN與KNN方法相耦合，提高了ANN預報能力不佳等問題；張珂等[14]將洪水預報智能模型應用于中國半干旱半濕潤地區，所建模型在半濕潤區典型流域可獲得良好的預報結果；張軒等[15]基于BP神經網絡算法建立經驗預報，模型預報精度可達乙級以上；Chang等[16]基于ANN構建了洪水淹沒多步預測模型；Fauzi等[17]同樣基于機器學習算法構建了海嘯淹沒的預報模型。這些研究表明，機器學習技術在洪水預報方面同樣具有廣闊的應用前景。

機器學習往往需要大量的訓練數據，目前洪水災害快速預報多基于水文站多年的實測數據，依靠完備的大數據進行訓練，但對于未發生過洪水或歷史淹沒資料匱乏的地區無法進行有效預測。為此，本文基于高精度水動力模型與機器學習技術，選取王茂溝流域為研究區域，以數值模型模擬數據作為驅動數據，探索構建實測洪水資料匱乏流域的山洪災害快速預報模型，旨在為緊急決策提供足夠的前置時間，協助決策者更好地采取應對措施。

1 研究區概況與降雨資料

1.1 研究區概況

本文選取陜西省榆林市綏德縣的王茂溝流域作為研究區域，該流域位于東經110°20′26″～110°22′46″，北緯37°34′13″～37°36′03″，總面積約為5.74 km2，王茂溝主溝長3.75 km，溝道平均比降為2.7%。流域海拔高度介于940～1 200 m，屬溫帶半干旱大陸性季風氣候，歷史最大年降水量為735.3 mm，多年平均降水量為475.1 mm，7—9月降水量可達全年降雨的64%，且多為短歷時強降雨，極易引起山洪、泥石流等災害。2012年7月15日及2017年7月26日均出現高強度暴雨，形成山洪，造成巨大經濟損失[18-19]。

地形精度對數值模擬至關重要，精度不足將無法反映實際地形特征，影響模擬的可靠性；精度過高對模擬精確性提高不大，但會嚴重延長模型的運行時間。經綜合考慮，將研究區域以5 m的水平分辨率劃分為232 037個網格，其數字高程圖見圖1，土地利用情況見圖2。同時，為更好地表征下墊面信息，將研究區根據不同的土地利用類型，基于最大似然法劃分為8類。預報模型采用Green-Ampt入滲模型，下滲系數根據文獻[20]確定，土地的曼寧系數根據文獻[21]確定，各土地利用類型具體參數見表1。

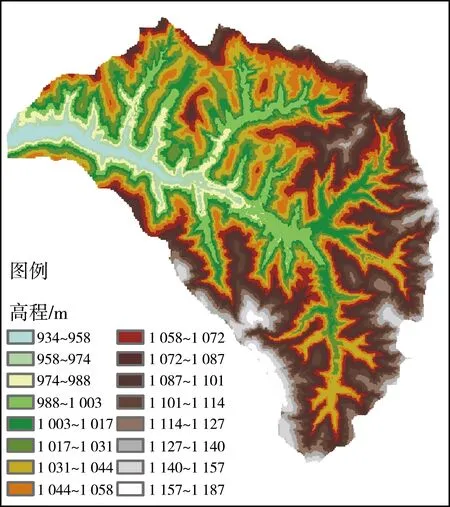
圖1 研究區域數字高程

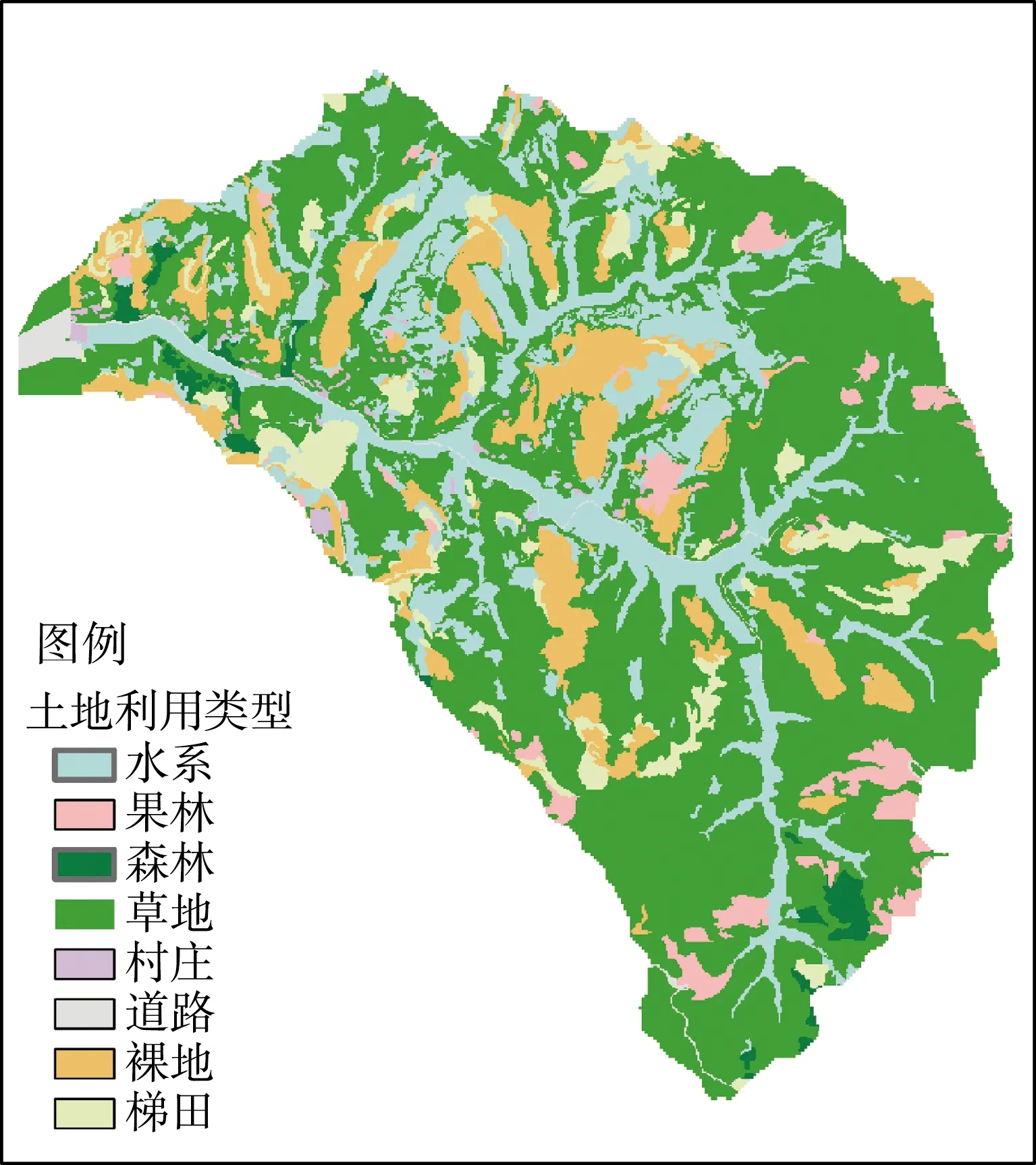
圖2 研究區土地利用情況

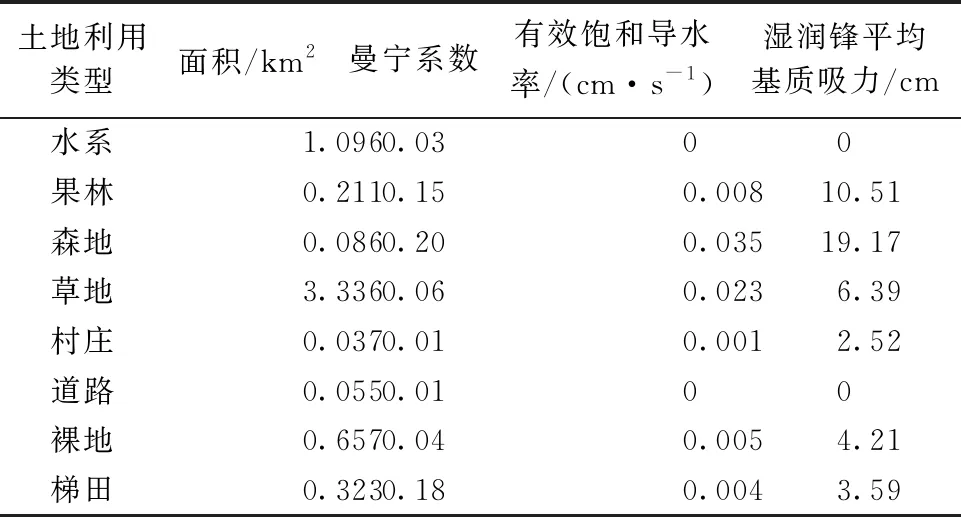
表1 各類型土地曼寧及下滲參數

1.2 降雨資料

本研究降雨資料時間分辨率取1 h。研究區實測降雨資料有限，僅用歷史數據無法完成模型訓練，因此，在進行模型訓練時，同時加入了歷史降雨資料與設計降雨資料。張茹等[22]研究表明GPM(global precipitation measurement)在強降水區域表現出較高的命中率和較低的誤報率，衛星產品對強降水的探測能力較優，故歷史降雨資料從GPM網站(https://gpm.nasa.gov)獲取[23]。本研究主要針對短歷時強降雨引發的山洪事件，與芝加哥雨型具有一定相似特征，薛宇雷等[24-25]通過芝加哥雨型生成器生成短歷時設計降雨，應用于周河流域及梅溪流域，均取得良好模擬效果。據此，研究選用芝加哥雨型生成器生成各類情況下的短歷時設計降雨。榆林市暴雨公式為

(1)

式中：i為暴雨強度，mm/h；p為重現期，a；t為降雨歷時，min。

2 快速預報方法

2.1 快速預報流程

為實現山洪災害快速精準預測，基于水動力模型，結合機器學習算法構建了山洪災害快速預報模型。預報流程圖如圖3所示，首先輸入地形數據、降雨數據等驅動水動力模型，獲得降雨-致洪數據，并將其劃分為訓練集與測試集，供機器學習算法擬合使用；同時，從降雨數據中提取特征參數，經相關性分析，獲取用于算法擬合的最終參數；通過機器學習算法擬合訓練集與特征參數，通過網格搜索算法尋找最優參數，獲取初步模型；再通過機器學習算法預報結果與水動力模型模擬結果獲得誤差矩陣，并將誤差作為訓練數據生成誤差修正模型；預報結果由機器學習算法預報模型與誤差修正模型共同生成，同時為降低單一算法自身局限性，將兩種算法(KNN算法和極限隨機樹(ERT)算法)結果按其在訓練集中評價指標得分進行權值分配，生成混合模型預報結果，并以測試集數據檢驗模型預報可靠性，若誤差過大，將參數調整后重新生成模型，直至預報精度達到要求后，得到最終預報模型。

圖3 快速預報流程

洪水淹沒范圍、過水斷面洪峰流量、最大流速以及最大水深是評價洪水風險的重要指標，因地形數據中可能存在的個別噪點會嚴重影響過水斷面的最大深度，因而本文主要采用洪水淹沒面積、斷面流量、平均流速及水深來評價模型的可靠性。

2.2 水動力模型

模型控制方程為耦合水文過程的二維淺水方程，忽略運動黏性項、科氏力、風應力及紊流黏性項。其對應的二維非線性淺水方程守恒格式的矢量形式表示如下：

(2)

其中

式中：q為變量矢量，包括水深h以及x和y方向的單寬流量qx和qy；u、v分別為x和y方向的流速；F和G分別為x、y方向的通量矢量；r為凈雨率；S為源項矢量；zb為河床底面高程；Cf=gn2/h1/3為河床糙率系數；n為曼寧系數。

模型選取對物理問題考慮最全面的動力波法進行地表洪水過程的模擬運算，通過基于Godunov格式的有限體積法進行空間離散求解二維淺水方程[26-27]，并運用Runge- Kutta方法構造具有二階時空精度的MUSCL(monotonic upwind scheme for conservation)型格式，確保物質守恒并有效解決不連續問題[28]。針對模擬過程中可能產生急變流與非連續等復雜問題，模型選用HLLC近似黎曼求解器對單元界面上的質量以及動量的通量進行求解。通過靜水重構法處理干濕邊界處可能出現負水深的問題[29]，并以流速替代單寬流量作為計算變量，可在水深低于或流速高于一定值時，將易失穩的二階格式有效地轉換為穩定的一階計算格式。保證計算精度的同時，將計算單元中的坡面源項轉換為該單元邊界上的通量，確保其在進行復雜地形計算時同樣滿足全穩條件。摩阻源項使用Hou等[30]優化的分裂點隱式法確保運算結果的穩定性。

該模型可對下墊面條件復雜區域進行高精度的雨洪模擬，并采用GPU(graphics processing unit)并行技術加速模擬計算過程，保障模型運算效率。侯精明等[31]對流域模擬數據與實測數據進行了可靠性對比，結果表明模型模擬性能良好；并且隨后的文獻[32]中另一區域模擬結果與實測數據同樣符合，再次驗證了模型的可靠性。

2.3 機器學習算法

機器學習是人工智能的核心，包含有SVM、邏輯回歸、決策樹、隨機森林、KNN等算法，本研究主要選用ERT算法及KNN算法構建山洪災害快速預報模型。

2.3.1ERT算法

ERT算法是Geurts等[33]于2006年提出的一種基于決策樹的集成學習算法。該方法類似于隨機森林算法[34]，通過自上而下的方式生成若干決策樹，運用多棵決策樹的綜合結果進行預測。訓練模型時每棵決策樹使用相同的訓練樣本；節點分裂時，省略對GINI系數或均方差的計算過程，采用參數完全隨機的方式提升算法的隨機性。因節點分裂屬性完全隨機決定，單棵決策樹的擬合精度通常較低，但綜合多棵決策樹結果，可大幅提升其預報精度。

在ERT算法的眾多參數中，模型性能對結點處隨機選擇的特征個數Max features及構成模型的決策樹深度Max depth較敏感。對于同一組訓練數據，Max features值越小，模型隨機性越強，同時對訓練樣本的輸出值的依賴性越弱。預測誤差隨Max depth的增加而減小，但Max depth值過大將造成模型的過擬合，致使模型在訓練集上可達到近乎完美的表現，但在測試集中會出現較大誤差，模型參數的選取需根據具體數據集確定[35]。

2.3.2KNN算法

KNN算法是Cover和Hart基于向量空間模型于1968年提出的一種機器學習算法[36]，該算法具有理論成熟、方法簡單以及魯棒性良好的優勢，可有效過濾訓練集中的噪聲。在KNN算法中，每個樣本均被視為Rn空間中的向量或坐標點，利用距離公式找出與待分類樣本最近的K個樣本，以此進行樣本估計。其主要步驟如下：

步驟1對已有樣本進行實例化，轉換為(x,f(x))的形式，其中x為樣本的特征參數，x由(x1,x2, …,xn)表示，xn為樣本的第n個屬性值，即特征參數的數量等于向量組成的維度，實例化后所有的樣本構成訓練集與測試集。

步驟2給定一個新的測試樣本xi，運用距離公式分別計算xi與訓練集中各個原本樣本之間的距離，并從中篩選出與xi距離最近的K個樣本。其距離公式主要有：曼哈頓距離公式、歐式距離公式及閔可夫斯基距離公式等，通過擬合效果綜合對比，最終選擇在訓練集及測試集上均表現良好的歐式距離公式：

(3)

式中：xi、xj為兩個樣本；xil、xjl分別為xi和xj的第l個特征值；L(xi,xj)為樣本xi和xj之間的歐式距離。

步驟3將選擇出的K個樣本與未知樣本的接近程度，按權重分配K個樣本的預測結果，并將其分配給新的測試樣本，作為預報值。

2.4 基于網格搜索的預報模型參數優化算法

機器學習算法對算法參數十分敏感，算法最大深度、最大特征數等參數的選取不合適將直接導致模型預報的失敗。為使預報模型能有效擬合所提供數據，研究采用網格搜索的方法對機器學習算法參數進行優選。網格搜索是一種窮舉型算法，可自動模擬各類參數的組合情況，進行多次模型訓練，并由交叉驗證進行誤差對比，最終找到訓練誤差最小的模型，確定出最適合訓練數據的最優的參數組合，進而通過對模型參數的優化提升模型的可靠性。研究中，交叉驗證系數選取為0.2，最終確定ERT算法的最大深度為10，誤差公式選取均方根誤差(RMSE)，最小分裂數為2；KNN模型K鄰近個數取為3，采用球狀樹算法進行數據分割，距離公式選擇為歐式距離公式。

2.5 誤差修正及模型評價指標

為降低由水動力模型及機器學習造成的誤差累積，利用水動力模型模擬結果與機器學習算法初步預報結果生成誤差矩陣，而后以降雨特征參數為輸入條件，誤差矩陣為輸出結果，運用機器學習算法建立降雨特征參數與誤差矩陣之間的對應關系，構建誤差修正模型。機器學習算法最終預報結果由初步預報結果累加上誤差修正模型所得出的對應誤差矩陣生成。同時，為降低由單一機器學習算法本身的缺陷產生的誤差，通過將KNN算法模型及ERT算法模型的模擬結果依據其在訓練數據集中的確定系數(R2)，進行加權分配，獲得混合模型預報結果。計算公式為

(4)

式中：RC為混合模型預報結果；RERT和RKNN分別為ERT模型和KNN模型各個網格上的預報結果；SERT和SKNN分別為ERT模型和KNN模型的R2值。

選擇R2、絕對平均誤差(MAE)和RMSE作為模型整體可靠性的評價指標。

3 結果與分析

在洪水安全應急管理中，決策者最關心的往往是洪水最大淹沒面積及洪峰流量情況，據此，通過水動力模型累計模擬108場降雨事件，其中歷史降雨事件為18場，設計降雨事件90場，獲得其雨洪過程作為樣本數據，運用ERT算法及KNN算法訓練生成快速預報模型，運用R2、MAE和RMSE評估預報整體性能。此外，在流域主溝道下游出口處選擇斷面，通過計算出口斷面的洪峰流量、流速及由流量與流速近似估算出的斷面平均水深對模型預報性能進一步進行復核。

3.1 水動力模型模擬性能驗證

快速預報模型的訓練數據均為水動力模型模擬結果，因此在進行模型構建時，需先對水動力模型的模擬性能進行驗證。模型驗證所用降雨資料為王茂溝水文站觀測數據，降雨開始于2012年7月15日00：25，降雨歷時為5 h，流量資料為王茂溝水文站實測數據，模擬時長為10 h，流域出口處的模擬流量過程與實測流量過程對比見圖4。由圖4可見，水動力模型模擬結果與觀測流量數據變化趨勢基本一致，流量峰值滯后約0.5 h，流量消退過程較觀測數據稍快，因遙測地形數據與實際地形存在差異，在進行土地利用劃分時產生了一定誤差，但模型總體效果良好，納什系數可達0.78，可有效模擬該流域降雨致洪過程。

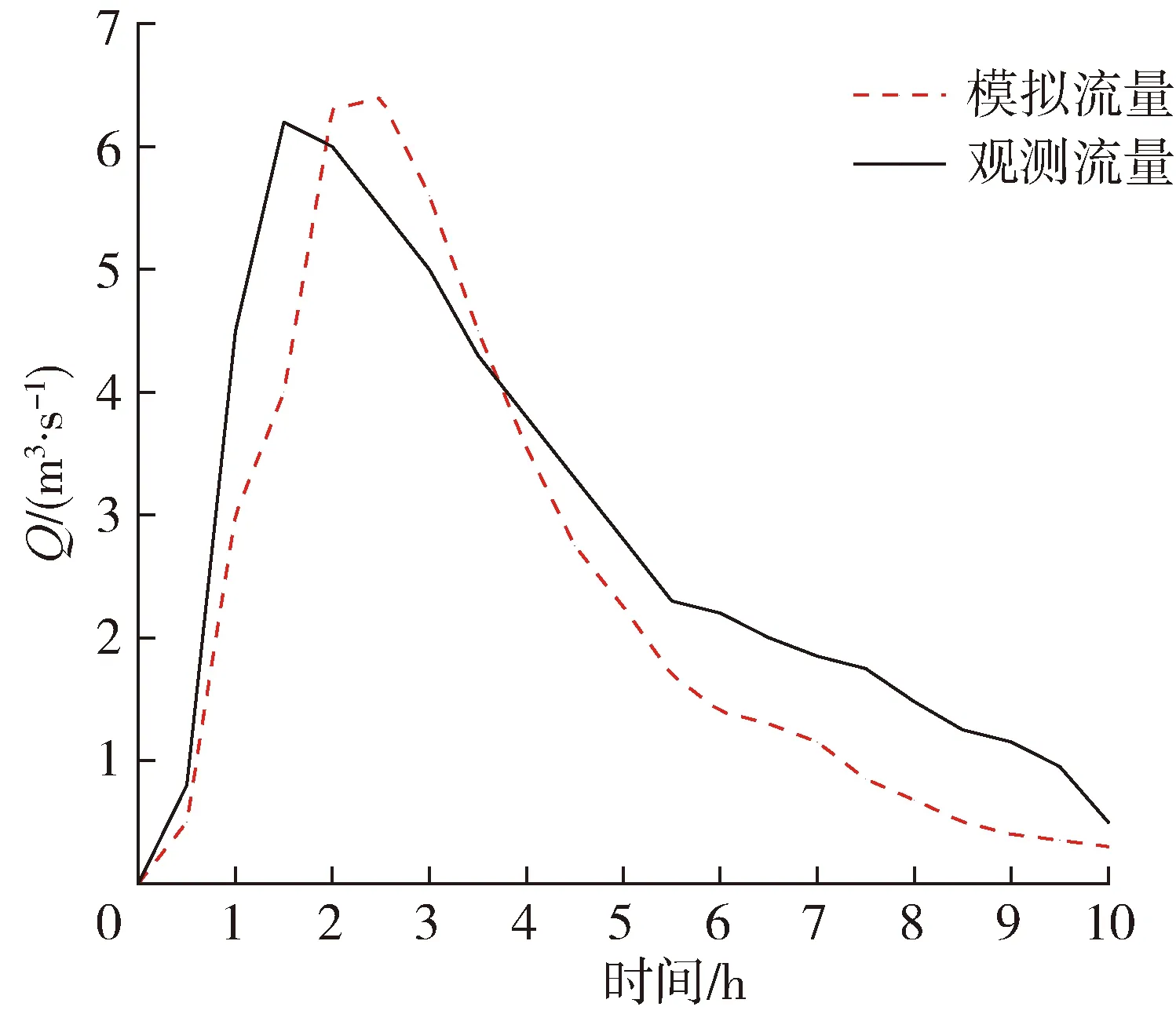
圖4 流域出口流量過程對比

3.2 降雨特征參數相關性分析

在進行機器學習訓練時，輸入參數的選取至關重要，合理優選參數即可保證模型精度，也可增強模型的時效性[37]。因此，研究選用皮爾遜相關性分析方法對模型所選降雨特征參數進行相關性分析。皮爾遜相關系數小于0.4時為弱相關、極弱相關或無相關，0.4～0.6為中等強度相關，0.6～1為強相關或極強相關。計算公式為

(5)

式中：ρxy為皮爾遜相關系數；σxy是參數x和y的協方差；σx、σy分別為x和y的方差。

選用流域總淹沒面積、總淹沒水量與所選降雨特征參數進行相關性分析，相關系數計算結果見表2。降雨重現期、降雨峰值、最大3 h降水量、最大5 h降水量、累計降水量及峰值前降水量與淹沒面積及淹沒水量都具有較強的相關性。總淹沒面積、總淹沒水量與降雨歷時的皮爾遜相關系數分別為0.054和0.096，屬于極弱相關或無相關，因此最終降雨特征參數舍棄降雨歷時，保留其余參數。

表2 降雨特征參數相關性分析

3.3 預報模型整體性能評估

選取93場降雨事件作為模型訓練數據，15場作為測試數據，分別運用ERT算法、KNN算法和混合算法構建山洪快速預報模型，3種模型的統計指標如表3所示。由表3可知，所有模型R2值均可達到0.90以上，說明模型能對數據形成較好擬合，可應用于洪水快速預報研究。在對水深進行模擬時，各預報模型均能獲得較好的得分，其中ERT模型略優，R2值為0.958 7，MAE值為0.001 4，RMSE值為0.010 0；在進行流速預報時，KNN模型預報效果最佳，R2值為0.951 7，模擬效果較好，ERT模型預報性能略差于KNN模型。混合模型在對水深及流速的整體預測上表現最好，R2值均達到0.95以上，MAE值和RMSE值均相對較小。

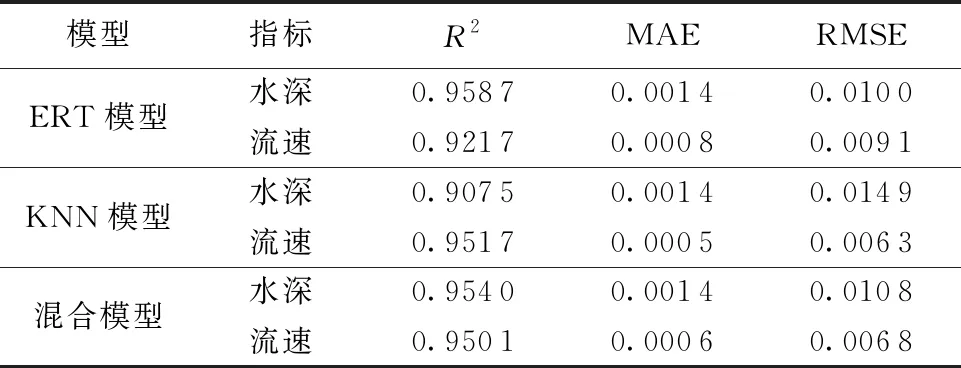
表3 快速預報模型評估指標值

圖5為水動力模型、KNN模型、ERT模型以及混合模型在出口斷面達洪峰流量時刻的水深圖，可以看出，KNN模型、ERT模型以及混合模型在出口斷面達洪峰流量時刻，對流域范圍內水深模擬結果與水動力模型模擬結果基本一致，能準確反映各處水深與各溝道中的行洪情況。

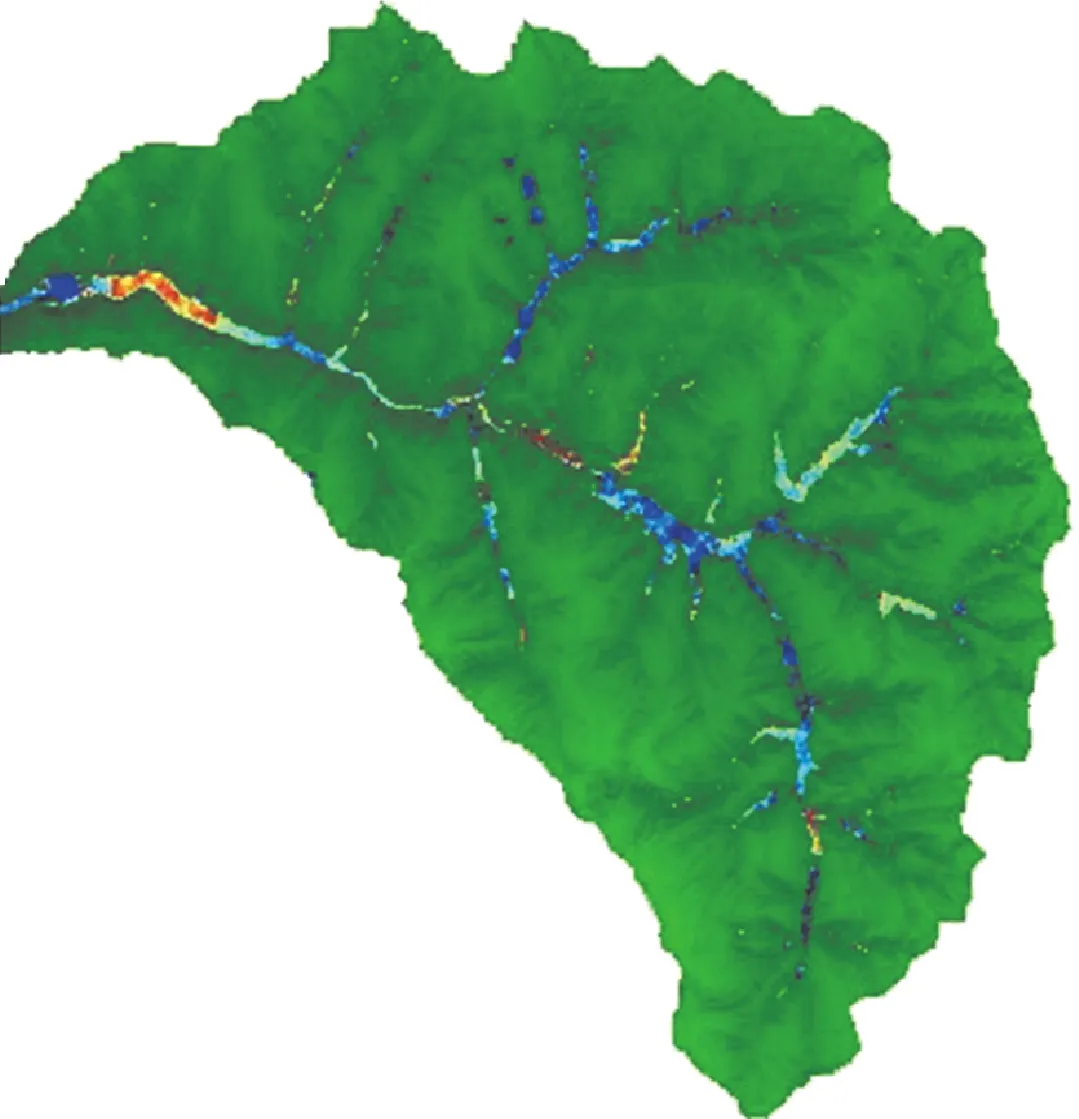
(a) 水動力模型

圖6為水動力模型、KNN模型、ERT模型以及混合模型對15場測試降雨事件模擬淹沒面積和淹沒水量的結果。圖7為KNN模型、ERT模型以及混合模型對淹沒面積、淹沒水量和平均水深模擬的相對誤差，忽略積水深度為10 cm以下的區域，在15場測試降雨事件中，模型對平均水深的預測最準確，對淹沒水量的預測效果稍差。由圖6可見，KNN模型、ERT模型以及混合模型模擬的淹沒面積變化情況與水動力模型模擬結果相同，其中KNN模型誤差較為穩定，平均相對誤差為0.39%，ERT模型平均相對誤差為1.14%，混合模型平均相對誤差為0.69%，均達到了近乎完美的擬合效果。淹沒面積與淹沒水量的平均誤差也可控制在5%以內，表明所構建的學習模型能較好反映山洪災害整體情況，預報性能良好。

(a) 淹沒面積

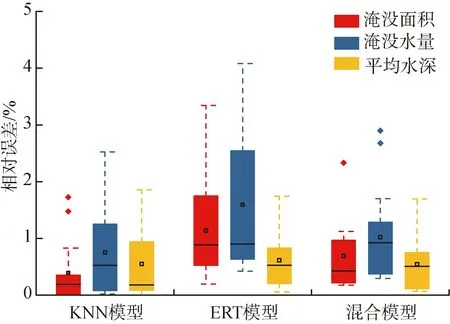
圖7 3種模型模擬相對誤差

水動力模型需從0時刻開始迭代運算，模擬單場降雨10 h致洪過程平均用時為1 688.4 s，KNN模型對15場降雨數據進行最大洪量預測累計用時為33 s，單場降雨平均用時為2.2 s。ERT模型速度略快，單場降雨平均用時為1.7 s，兩類模型均能在極短時間內給出預測結果。混合模型需要綜合ERT模型及KNN模型結果，因此模擬用時稍長，單場降雨平均用時約為4.1 s，亦可滿足快速山洪快速預報需求。

3.4 流域出口斷面分析

因山區地形起伏較大，在將地形網格化進行洪水模擬計算時，地勢高的區域降雨將迅速向低洼區域匯集，這會使地勢高的區域出現大量積水量極小的網格，因此預報模型在該區域將會達到近乎完美的預報效果，在運用傳統指標進行模型可靠性評估時將會過高估計模型的實際預報效果。因此，本文以流域出口斷面作為研究斷面，通過分析出口斷面的流量、流速及平均斷面水深進一步驗證模型預報性能。在15場降雨事件中，盡管模型在整體指標評估中均得到了較高的分數，但在實際的出口斷面處，模型性能仍存在一定差異。4種模型在出口斷面處平均水深、平均流速和斷面流量模擬結果見表4。

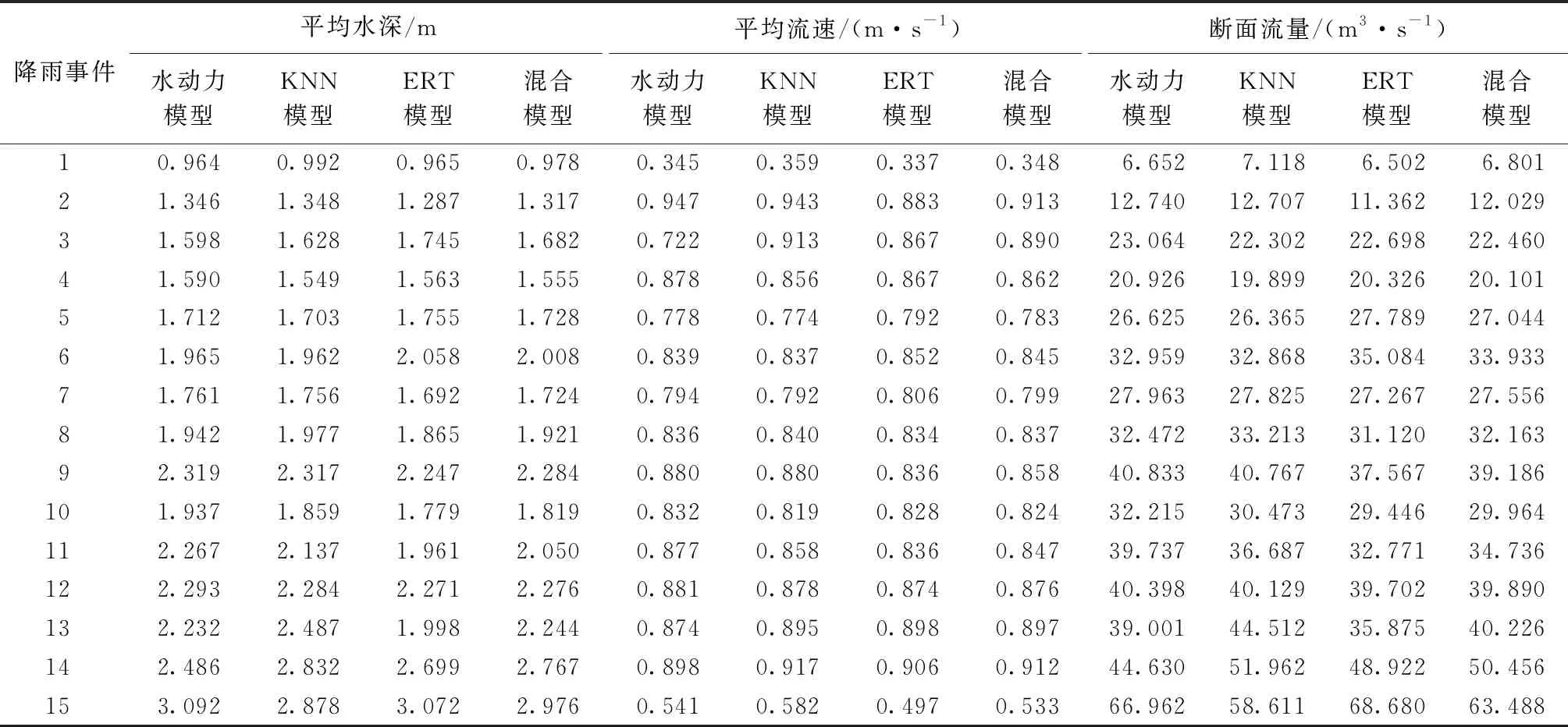
表4 出口斷面處平均水深、平均流速和斷面流量模擬結果

圖8為模型在出口斷面的平均水深、平均流速和斷面流量的相對誤差。由圖8(a)可見，3種模型對斷面平均水深預測的平均誤差均小于10%，其中KNN模型平均誤差為3.51%，ERT模型平均誤差為5.98%，KNN模型整體誤差較小；兩種模型在對個別場次降雨模擬時仍然存在較大誤差，KNN模型最大誤差為13.90%，ERT模型最大誤差為13.51%。混合模型平均誤差為3.39%，最大單場降雨誤差為11.27%，有效綜合了兩種算法結果，降低對個別場次降雨致洪信息的誤報。由圖8(b)可見，3種模型在進行流速預測時誤差均較小。其中，KNN模型對斷面流速預測性能最佳，平均誤差為1.85%，比ERT模型低1.03%，同時，最大誤差也最小，為6.00%。混合模型平均誤差為1.92%，比KNN算法模型預報性能略差，這是由于在對流速進行預測時，KNN模型擬合效果普遍高于ERT模型，在這種情況下混合模型通過綜合兩種模型模擬結果對誤差的校正效果不明顯。由圖8(c)可見，3個模型對于斷面流速及水深的預測準確性要優于斷面流量，這是由于斷面流量是通過構成斷面網格上的水深、流速計算求得，因此存在一定的誤差累積現象，導致模型對流量的預報性能稍差。但所建混合模型對斷面流量最大誤差可控制在15%以內，平均誤差為4.50%，低于10%，仍具有較高準確性，可滿足緊急決策需求。

(a) 平均水深

4 結 論

a.經評價指標分析，本文選取的機器學習算法在進行山洪災害預報時均能有較好性能，進行水深模擬預測時，各模型預報均能獲得較好的得分，其中ERT模型最佳；進行流速預報時，KNN模型預報效果較好，ERT模型略差于KNN模型，混合模型可有效綜合預報結果，可將整體誤差控制在5%以內。

b.根據流域出口斷面特征信息，算法對斷面平均流速預測差距不大，KNN算法表現最佳，平均相對誤差為1.85%，混合模型對誤差降低不明顯；在進行斷面水深及流量預測時，算法預報效果差距較大，KNN算法模擬平均水深及斷面流量平均誤差分別為3.51%和5.10%，ERT算法表現稍差，平均誤差均分別為5.98%和6.07%，混合模型對誤差校正效果明顯，最終平均誤差分別為3.39%和4.50%，可為應急決策提供可靠依據。

c.所建模型單場降雨平均模擬時間可控制在10 s以內，可為緊急決策爭取大量前置時間，協助決策者更好地采取應急管理措施。