基于特性參數矩陣的混合多端直流系統可靠性分析

徐攀騰，喻文翔，朱博，宋述波，鄭星星，樊友平

(1. 中國南方電網有限責任公司超高壓輸電公司廣州局，廣州510500；2. 武漢大學電氣與自動化學院，武漢430072)

0 引言

我國電力能源消費與供給分布極不均衡，電力輸送是目前實現能源平衡的一種有效方式[1 - 2]。直流輸電以其在遠距離大容量輸電方面的獨特優勢在西電東送中扮演重要角色[3 - 6]。常規換流器和柔性直流換流器的結合能將各自的優勢最大化，具有巨大的經濟技術效益，隨著輸電走廊資源的日趨緊張，特高壓混合多端直流輸電系統將有望成為直流輸電系統發展的主流趨勢。與此同時，世界各地的停電事故頻頻發生[7]。2016年6月肯尼亞有470萬戶家庭和企業停電超過4 h[8]。而特高壓直流輸電系統有助于減少故障的傳播，其可靠性已成為影響大電網可靠性的重要因素[9 - 10]，對特高壓直流輸電系統進行可靠性評估成為電力系統規劃、設計和運行的一個十分重要的環節。

特高壓直流輸電系統可靠性評估中主要采用的方法可歸類為解析法和模擬法。解析法使用直接數值解通過數學模型計算可靠性指標，典型的有頻率持續時間法、故障樹法、串并聯網絡分析法和狀態空間圖法等[11 - 15]。當目標系統具有相關故障和修復模式并且其組件以統計獨立的方式運行時，馬爾可夫法非常有用。但在多數情況下，馬爾可夫法不一定能夠正確識別所有的狀態和轉換過程，因此難于構造多狀態系統的狀態空間圖。典型的模擬方法如蒙特卡洛法，是通過模擬系統的實際過程和隨機行為來估計可靠性指標。這種方法的主要缺點是在推導和模擬過程中需要大量的資源。尤其是在元件可用性較高時，為了獲得準確且可理解的結果，通常需要進行大量的模擬試驗。容量中斷概率表(capacity outage probability table, COPT)分析方法應用逐漸流行起來[16]。但如果系統的組件數量龐大且具有多個狀態，COPT的生成將很復雜，需要推導很長的方程式，導致計算非常復雜。

相較兩端直流輸電系統，混合多端直流輸電系統具有更多的元件和更復雜的運行方式，系統事件趨于復雜，常規評估方法已不能很好地對混合多端直流輸電系統進行可靠性評估。同時，隨著我國特高壓直流輸電工程運行維護經驗的日益豐富，我國特高壓直流輸電系統的可靠性得到極大改善。以往文獻中可靠性參數的適用性下降，為了得到更準確的可靠性評估結果，需要重新對其進行整理。

基于上述原因，本文建立了特高壓混合多端直流輸電系統的可靠性評估模型，通過查閱大量文獻搜集2013年以來直流輸電系統的可靠性統計數據，分析得到特高壓混合多端直流系統評估模型中各設備的可靠性參數，之后提出一種基于特性參數矩陣的可靠性分析算法，解決了常規方法對混合多端直流系統進行可靠性評估分析時存在的算法復雜且計算速度慢的問題。最后基于一個特高壓混合多端直流輸電系統算例，利用常規方法和本文所提方法對其進行可靠性評估，通過對比可靠性計算結果證明了本文所提可靠性評估方法的高效性和實用性。

1 特高壓混合多端直流輸電系統可靠性評估模型

1.1 可靠性評估模型建立

圖1為一個特高壓混合多端直流輸電系統，該系統主要分為3個部分：常規直流送端、常規直流受端和柔性直流受端。其主要組件包括：交流濾波器(AC filter，ACF)，其中兩組A型、一組B型、一組C型，交流斷路器(AC breakers，Brk)，換流變壓器(converter transformer，Tm)，換流閥(valve，Vlv)，平波電抗器(smoothing reactor, SR)，直流濾波器(DC filter, DCF)和直流輸電線路(DC transmission line, DCTL)。系統送端和受端均采用雙極配置結構，可以看作是兩個并聯的單極配置。如果一極中斷，仍然可以在降額狀態下由剩余極和接地電流運行直流輸電系統。

圖1 特高壓混合多端直流輸電系統結構圖Fig.1 Structure diagram of UHV hybrid multi-terminal DC transmission system

為進行可靠性評估分析，將圖1所示系統以框圖的形式表示，其中各系統組件分別以串聯、并聯的形式連接在一起。圖2為以該方式得到的特高壓混合多端直流輸電系統的可靠性框圖。該框圖主要說明了系統中各組件發生故障對系統整體可靠性的影響。例如，交流濾波器故障會導致輸送容量降低，而一條直流輸電線路故障會導致單極停運。

圖2 特高壓混合多端直流輸電系統可靠性框圖Fig.2 Reliability block diagram of UHV hybrid multi-terminal DC transmission system

常規直流受端換流站與柔性直流受端換流站為并聯關系。分別計算各組件的可靠性指標，然后按照圖2的系統可靠性框圖進行組合即可得到整個特高壓混合多端直流輸電系統的可靠性指標計算結果。各組件系統事件對應的容量狀態由圖3確定。

圖3 特高壓混合多端直流輸電系統容量狀態確定框圖Fig.3 Block diagram of capacity status determination of UHV hybrid multi-terminal DC transmission system

結合圖3可得到各元件或子系統故障對系統可靠性的影響，系統處在兩受一送的運行方式，如果受端2的正極換流變壓器故障，則造成受端2的單極停運，受端2的負極和送端1的雙極還將正常運行。由于只有唯一的送端，因此，若送端因單極元件故障導致單極停運，則會造成系統的單極停運。

1.2 特高壓直流輸電系統元件可靠性參數統計

故障率是指元件年度故障次數的統計平均值，修復時間是指元件多次故障修復時間的平均值，而修復率則是修復時間的倒數。由于特高壓直流輸電系統結構復雜，包括換流變壓器、閥組、平波電抗器、直流輸電線路、交流濾波器、直流濾波器和控制保護系統等，在對特高壓直流輸電系統進行可靠性評估時需要知道所有這些元件的多年平均故障率和修復率參數。本文在可靠性評估中采用多來源可靠性數據搜集，所采用的原始參數主要來源于國家能源局電力可靠性管理和工程質量監督中心。本文在求取各直流元件可靠性參數時，進行了如下數據處理。

1)鑒于電氣元件運行過程中故障率服從浴盆曲線分布，而我國投運的特高壓直流工程都尚未進入衰耗期，本文在可靠性參數計算過程中，剔除各直流工程投運第一年的故障記錄，如果某特高壓直流工程投運時間不足一年，則此工程的運行記錄不作為可靠性參數計算的參考數據。

2)將可靠性數據的動態性質納入考慮范圍。

3)為提高數據質量，對相應數據進行分解和剔除。

結合上述計算分析，得到表1和表2中常規直流工程和柔性直流工程的元件可靠性參數。

表1 常規直流工程元件可靠性參數Tab.1 Reliability parameters of conventional DC engineering components

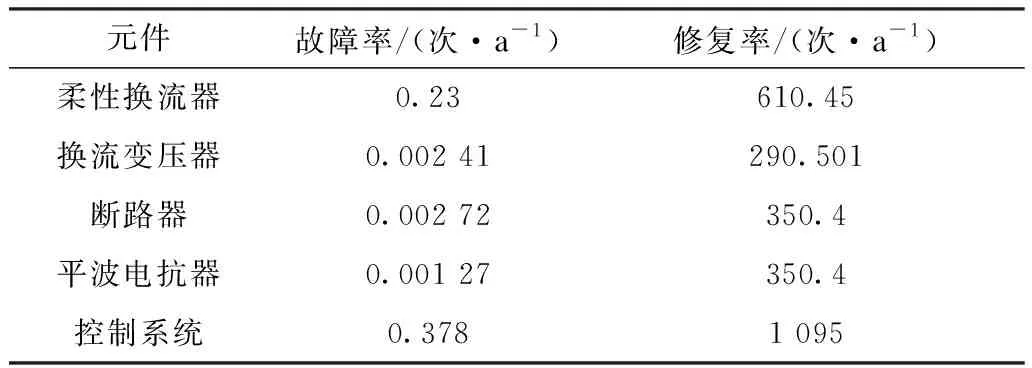
表2 柔性直流工程元件可靠性參數Tab.2 Reliability parameters of flexible DC engineering components

2 特高壓混合多端直流輸電系統可靠性評估算法

基于特性參數矩陣的系統可靠性(system re-liabi-lity based on characteristic parameter matrix，SRCPM)方法使用特性參數矩陣來計算系統的失效概率[17 - 21]。SRCPM方法普遍適用于一般系統，由于系統事件是通過簡單的矩陣計算來處理的，因此系統事件(故障條件)的定義不會影響計算的復雜性。由于這些特性，SRCPM方法能夠很好適用于特高壓混合多端直流輸電系統的可靠性評估分析。

為了表示一般的系統事件，本文定義事件向量c，如果ej屬于系統事件，則第j個元素為1，否則為0。通過以下迭代矩陣過程獲得特性參數矩陣C[i]如式(1)—(2)所示。

C[1]=Is1×s1

(1)

(2)

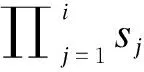
此外，可以通過以下順序矩陣計算來構造具有n個多態元件的系統的概率向量：

(3)

式中：p[i]為第i個元件的概率向量；pi(j)為第i個元件處于第j個狀態的概率。

由于各個集體事件ej相互排斥，系統事件Esys的概率(p(Esys))為屬于系統事件ej的概率之和。系統事件Esys的概率通過矢量計算來計算：

(4)

式中：cEsys為系統事件Esys下的事件向量；列向量p為包含pj的概率向量。

接下來用一個示例系統解釋式(1)—(4)中的矩陣過程。假設有一個3組件系統，其中每個組件都有2個不同的狀態，即非故障(Ei(1))和故障(Ei(2))。相應的23=8個MECE事件為：

e1=E1(1)∩E2(1)∩E3(1),e2=E1(2)∩E2(1)∩E3(1),

e3=E1(1)∩E2(2)∩E3(1),e4=E1(2)∩E2(2)∩E3(1),

e5=E1(1)∩E2(1)∩E3(2),e6=E1(2)∩E2(1)∩E3(2),

e7=E1(1)∩E2(2)∩E3(2),e8=E1(2)∩E2(2)∩E3(2)

(5)

圖4所示為8個MECE事件的樣本空間。

3個元件事件E1(1)、E2(1)和E3(1)的概率為：

(6)

式中：P1、P2、P3分別為3個元件事件E1(1)、E2(1)和E3(1)的概率；p1、p2、p3、p4、p5、p6、p7分別為第i(i=1,2,…,7)個MECE事件的概率。

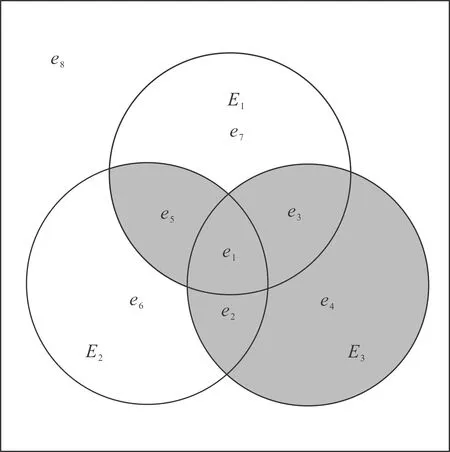
圖4 3個雙態元件系統的樣本空間Fig.4 Sample space for three two-state element systems

元件事件發生的任何交集的概率均以構成交集事件的基本MECE事件的概率之和給出：

(7)

式中：P(E1(1)∩E2(1))和P1,2為第1個和第2個組件均為非故障狀態的概率；P(E1(1)∩E3(1))和P1,3為第1個和第3個組件均為非故障狀態的概率；P(E2(1)∩E3(1))和P2,3為第2個和第3個組件均為非故障狀態的概率；

三元件事件的事件向量是通過公式(1)和(2)中給出的迭代矩陣過程獲得的。

(8)

通過式(3)中給出的順序矩陣計算構造相應的概率向量如下：

(9)

之后考慮圖4中陰影區域所示的系統事件Esys=(E1(1)∩E2(1))∪E3(1)。 事件E的互補事件向量可通過式(10)獲得。

cEi(2)=1-cEi(1)

(10)

對于n元件系統，事件E1,E2,…,En的交集和并集分別是：

cE1(1)∩…∩En(1)=cE1(1).*cE2(1).*….*cEn(1)

(11)

cE1(1)∪…∪En(1)=1-(1-cE1(1)).*….*(1-cEn(1))

(12)

使用矩陣運算，獲得事件向量cEsys如下：

(13)

式中“.*”為MATLAB中用于逐元素乘法的運算符。最后，概率P(cEsys)由式(4)計算：

(14)

本文采用布爾代數來獲取任何系統事件。對于圖4中陰影區域所示的系統事件Esys=(E1(1)∩E2(1))∪E3(1)， 其事件向量可以通過以下布爾運算獲得：

(15)

布爾邏輯運算符“&”(AND)和“|”(OR)用于標準比較和組合邏輯表達式。在具有較多組件的系統中，使用布爾算子的優勢更加明顯，使用布爾代數獲取系統事件比文獻[21]中提出的操作更為實用，從而有助于進行分析。為減少計算內存，在要分析的系統僅由雙態組件組成的情況下，可以通過構建特性參數矩陣Cl直接獲得元件事件的事件向量。它是一個按照從(2n-1)～0順序的二進制降序計數矩陣。對于圖1的混合多端直流輸電系統，特性參數矩陣如式(16)所示。

(16)

式中：矩陣Cl的行根據二進制數字系統以降序排列；并且矩陣的每一列代表一個組件，每個組件具有兩個可能存在的狀態，各事件(即cE1,cE2,cE3)從左到右以升序排列。將布爾運算符NOT和XOR用于更復雜的元件狀態以減少內存的使用。

系統的概率向量通過式(17)獲得：首先，用對應的概率pi(1)和pi(2)分別替換矩陣Cl中的1和0來形成矩陣Cp。

(17)

而后通過將每一行的元素相乘，從Cp得出概率向量p：

(18)

使用式(16)—(18)并以相同的操作Csys=(C1&C2)|C3為例，所獲得的可用性結果為：

(19)

最終重排后的結果等于式(14)中給出的結果。

3 算例分析

本節針對特高壓混合多端直流輸電系統，使用常規方法和本文所提方法推導估計系統狀態概率的方程式，并進行了比較，以確定本文所提方法的優勢。同樣，將通過常規方法獲得的方程式編程用于計算機仿真，并運用非序貫蒙特卡羅算法，以便根據計算效率比較方法的性能。研究案例使用兼容PC的2.60 GHz，Intel Core I7-6700HQ處理器，8 Gb RAM，Windows 10和MATLAB?2014a進行。

通過將SRCPM方法應用于雙態組件，可以估算出系統各端的各容量狀態的可用性值。為了簡明地描述SRCPM方法的應用，假定在常規整流站與逆變站的設備是相同的，因此兩個站的可用率是相同的，接下來通過將SRCPM方法應用于送端來獲得整流站的可靠性。

表3 各容量對應的失效元件Tab.3 Failed components corresponding to each capacity

為了獲得送端部分的可用率，所有元件均按如圖5所示進行編號。該部分包含16個元件，每個元件具有兩種不同的狀態：非故障和故障。獲得對應的特性參數矩陣Cl， 其大小為(216×16)。 所得Cl矩陣的列向量表示元件事件的事件向量，即C1,C2,…,C16。 向量p是按照前面所述步驟獲得的，其大小為(216×1)。 此處Cl和p不再詳細列寫。

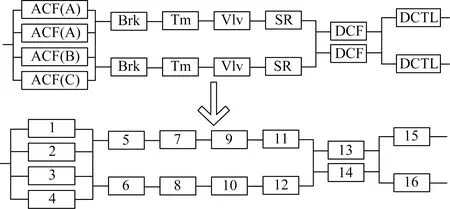
圖5 常規直流送端及其編號組件的可靠性框圖Fig.5 Reliability block diagram of conventional DC sending-end and its numbered component

應用布爾代數式從元件的事件向量中獲取表示送端各種容量狀態的不同系統事件。布爾運算是根據兩端失效元件所引起不同系統狀態的要求給出的，具體如表3所示。生成的系統事件和概率向量以及送端容量狀態的可用率如表4所示。表5為通過常規方法獲得的每個系統事件的運算過程。可以看出，與常規方法相比，在這一階段通過基于特性參數矩陣的方法推導方程式相對容易。特別是在比較容量為0.5 p.u.時的方程式，可以更清楚地注意到這一點。

表4和表5兩種方法的比較結果非常接近，意味著基于特性參數矩陣的可靠性方法是有效的。基于特性參數矩陣的可靠性方法的優點在于，由于使用了二進制矢量和布爾運算符，該方法可通過較為簡單的方式獲得較短的方程。

接下來評估柔性受端換流站的可靠性。柔性直流受端站由8個雙態元件組成：斷路器、換流變、VSC換流閥、平波電抗器。這些元件分別編號為1→8，其中正極為1→4，負極為5→8。遵循上一節中所述的雙態元件系統應用SRCPM方法的相同過程，獲得矩陣Cl和向量p，其大小分別為(28×8)和(28×1)。 生成的Cl矩陣列向量表示組件事件的事件向量C1,C2,…,C8。 柔性受端有4種狀態：正常運行(容量為1 p.u.)、正極停運(容量0.5 p.u.)、負極停運(容量0.5 p.u.)和雙極停運。表6所示為計算柔性受端的事件向量的布爾方程式和通過常規方法計算可靠性所需的方程。兩種方法的計算結果如表7所示。

表4 SRCPM方法所得常規直流站可靠性Tab.4 Reliability of conventional DC station obtained by SRCPM method

表5 常規方法所得常規直流站可靠性Tab.5 Reliability of conventional DC stations obtained by conventional methods

表6 SRCPM方法與常規方法計算柔性受端可靠性方程Tab.6 Reliability equations of flexible end of SRCPM method and conventional method

表7 SRCPM方法與常規方法所得柔性受端可靠性結果Tab.7 Reliability results of flexible end obtained by SRCPM method and conventional method

表8 計算系統事件向量的布爾方程和常規方程及相應結果Tab.8 Boolean equations and conventional equations for calculating system event vectors and corresponding results

根據上述過程得到特高壓混合多端直流輸電系統中兩個受端和一個送端的可靠性值，之后通過兩個階段應用SRCPM方法來評估整個特高壓混合多端直流輸電系統不同容量狀態時的可靠性。在第一階段，將SRCPM方法應用于常規直流受端和柔性直流受端，將兩個子系統定義為兩個多狀態組件，構成兩組件系統。將以常規直流受端定義的多狀態組件編號為1，以柔性直流受端定義的多狀態組件編號為2。這意味著s1=7=和s2=3。 按照式(1)和(2)中描述的過程獲得相應特性參數矩陣如下：

(20)

式中：矩陣C[2]的大小為(21×10)。C[2]的前7列表示常規受端的事件向量，用符號C1,C2,C3,…,C7表示。剩下的3列表示柔性受端的事件向量，并用C8,C9,C10表示。利用這些事件向量，可以組合為受端的每個容量狀態制定系統事件向量。根據式(1)—(2)中描述的過程獲得相應的概率向量：

(21)

式中：概率P1(j)和P2(j)分別為表4和表6中的概率。

接下來，根據系統事件向量和概率向量，利用式(3)計算每個容量狀態的可用性值。表8展示了用于獲取系統事件向量的布爾方程式，并為每種容量狀態推導了可用性值。以及從常規方法中獲得的方程式和常規方法獲得的可靠性值，以驗證結果。

在第2階段，將SRCPM方法用于上面分析的兩組件系統和常規送端組合。同樣將其定義為一個由兩個多狀態組件構成的系統。常規送端組件編號為1，第一階段得到的子系統組件編號為2，這意味著s1=7和s2=17。 按照針對常規直流受端和柔性直流受端組合進行上述相同過程，獲得相應的矩陣C[2]和概率向量p[2]。C[2]的前7列代表常規送端的事件向量，用符號C1,C2,…,C7表示。其余17列代表子系統的事件向量，用C8,C9,…,C24表示。重復上述過程，計算特高壓混合多端直流輸電系統每個容量狀態的可用率，并與常規方法獲得的結果如表9所示。

表9 混合多端直流輸電系統可靠性計算結果Tab.9 Reliability calculation results of hybrid multi-terminal DC transmission system

通過對常規方法和SRCPM方法得到的可靠性評估結果進行對比分析，在本算例中，盡管兩者之間的評估值差異并不顯著，但在CPU時間方面，本方法比常規方法效率更高，驗證了本文所提方法的高效性和實用性。基于特性參數矩陣的可靠性評估方法很適合用于特高壓混合多端直流輸電系統的可靠性評估，與許多常規方法相比，它在分析復雜系統的情況下具有更好的適用性。

4 結語

本文提出了一種基于特性參數矩陣的特高壓混合多端直流輸電系統的可靠性評估方法，經算例驗證，能夠很好地解決常規方法在對特高壓混合多端直流輸電系統進行可靠性評估時存在的方程構建冗長、計算效率低等問題。

本文所提方法通過簡單的矩陣計算和布爾運算來計算系統可靠性，通過算例驗證，在計算結果相近的情況下，相較于常規方法可縮短接近一半的CPU計算時間，在計算速度和簡便性方面具有較大優勢。隨著未來特高壓混合多端直流輸電系統的發展，實際工程結構趨于復雜，本文所提方法可進一步發揮其運算高效的優勢，大大提高可靠性分析效率，因此具備良好的高效性和實用性。由于所采用的元件可靠性參數均來自直流輸電系統設備，對交流系統可靠性評估的適用性還需要進一步驗證。