基于改進蟻群與動態窗口法的AGV動態路徑規劃

楊 周，劉海濱

北京工業大學 材料與制造學部，北京 100124

路徑規劃是自動導引車（automatic guided vehicle，AGV）研究領域的一個重要課題，其目的是在有障礙物約束的環境下，根據已知的起點與終點，以最短路徑、最短時間等為目標尋找一條最優或接近最優的安全、無障礙路徑[1-2]。根據應用場景的不同，可將路徑規劃算法分為全局靜態路徑規劃算法和局部動態路徑規劃算法。全局靜態路徑規劃算法主要應用于全局信息已知的靜態環境，常用的算法有Dijkstra算法[3]、A*算法[4]、蟻群算法[5]等；局部動態路徑規劃算法主要應用于全局信息未知或部分已知的動態環境，常用的算法有動態窗口法[6]、強化學習[7]等。

蟻群算法因具有良好的搜索能力、正反饋特性、并行計算、易與其他算法融合等特性，在全局靜態路徑規劃中得到大量應用。但傳統蟻群算法也存在搜索時間長、易陷于局部最優、前期盲目搜索導致收斂性差等缺陷。葛志遠等[8]針對傳統蟻群算法搜索效率低，耗時長等問題，通過改進啟發函數確定搜索方向并利用優勝劣汰機制更新全局信息素，保證算法多樣性的同時提高算法收斂速度；王曉燕等[9]針對傳統蟻群算法各節點初始信息素均勻分布導致算法初期搜索范圍大，收斂性差等問題，提出初始信息素不均衡分配策略，降低了初期搜索盲目性，提高了算法搜索效率。

動態窗口法是常用的局部動態路徑規劃算法，具有很好的躲避動態障礙物能力，可以實時在線路徑規劃，且路徑較為平滑，符合AGV運動特征。但由于缺少全局信息的指導，規劃路徑質量較差，且經常無法到達目標點。殷紹偉等[10]利用改進的A*算法改進蟻群算法，然后融合滾動窗口法進行局部實時路徑規劃，最后使用貝塞爾曲線對路徑進行平滑度處理，使路徑更加接近AGV實際運動特征；槐創鋒等[11]將傳統A*算法的3×3搜索領域擴展到7×7，解決了傳統A*算法折點多，路徑不平滑的問題，然后根據全局最優路徑設計動態窗口評價函數，實現了機器人在復雜環境下的實時動態路徑規劃。

由上述文獻可知：全局靜態路徑規劃算法可以有效利用全局信息規劃出全局最優路徑，但無法躲避動態障礙物；局部動態路徑規劃算法可以實時在線規劃路徑，有效躲避動態障礙物，但由于缺少全局信息，易陷入局部最優解，經常出現無法到達目標點的現象。針對這兩類算法的缺陷，許多學者將兩類算法融合，并在實時動態路徑規劃方面取得了較好的效果。為在動態環境中實時規劃全局最優路徑，本文參考融合思想提出了一種結合改進蟻群算法和動態窗口法的全局動態路徑規劃算法。首先，對蟻群算法提出改進：初始信息素不均勻、雙向分布，為蟻群算法雙向搜索提供大體方向；引入放大系數A增大相鄰柵格啟發信息差異，增大螞蟻選擇更優節點的概率；更新信息素選擇最優路徑時考慮轉彎次數的影響，得到更平滑的路徑，提升AGV運行效率。然后，設計新的動態窗口法距離評價子函數并動態設置AGV初始航向角。最后，提取改進蟻群算法規劃的全局最優路徑上的轉折點作為改進動態窗口法的子目標點，引導動態窗口法沿著全局最優路徑方向進行實時動態路徑規劃，最終實現有效躲避動態障礙物的同時規劃全局最優路徑。

1 蟻群算法及改進

1.1 蟻群算法工作原理

蟻群算法是一種來源于自然界的智能隨機搜索算法，有很強發現較優解的能力[12]。其工作原理為螞蟻在覓食過程中通過釋放信息素進行群體間信息傳遞，信息素濃度與路徑長度成反比，濃度越高表示路徑越短，該路徑被其他螞蟻選擇的概率就越高，通過這種正反饋機制能夠很快搜索出到達目標位置的無碰撞最優路徑。

1.2 蟻群算法的改進

1.2.1 初始信息素不均勻、雙向分布

傳統蟻群算法初始信息素采用均勻分布的方法，簡單易行，但各柵格信息素濃度相同導致算法初期存在盲目搜索，收斂性差等問題[13]。由于雙向搜索策略能大大提高算法全局搜索能力、加快前期搜索效率、增大前期有效解，因此本文在基于雙向搜索策略下提出初始信息素不均勻、雙向分布，為蟻群雙向搜索提供大體方向，避免算法初期盲目搜索、收斂性差等問題，并滿足任意起點與終點的應用場景。

假設AGV的起點坐標為( xS,yS)，終點坐標為( xE,yE)，則過起點與終點的直線可以用方程L表示：

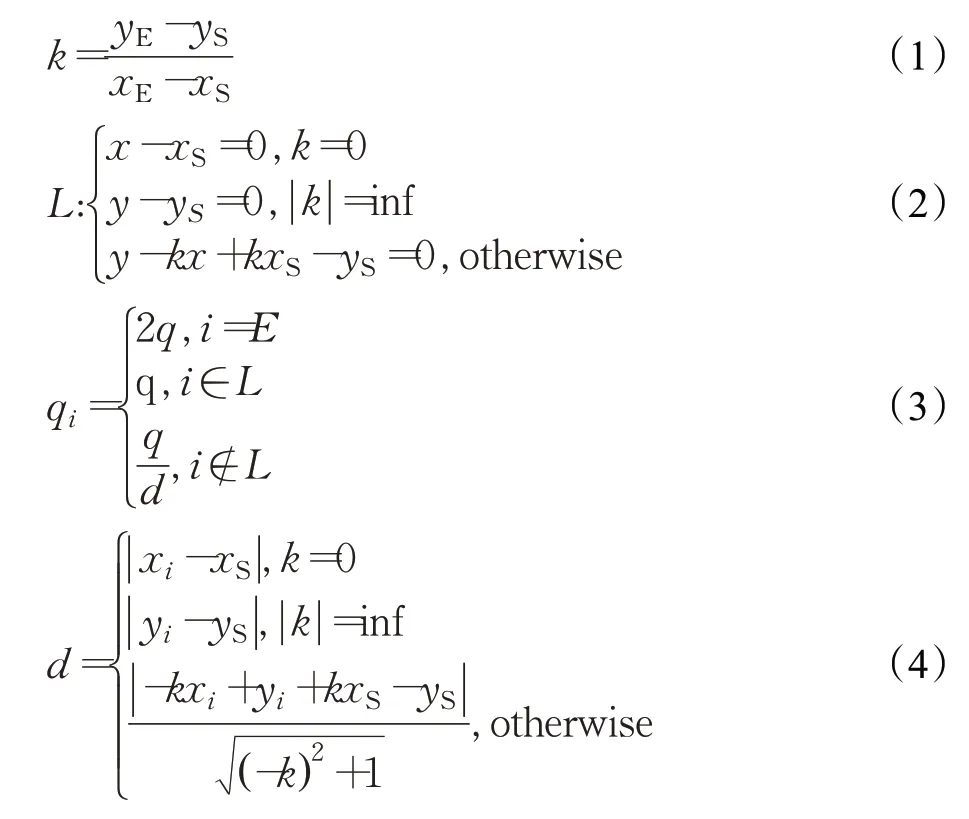
式中，k為連接起點與終點的直線斜率；q為初始信息素均勻分布時的初始值；i為柵格點數；qi為改進后各柵格信息素初始值，d為節點i到方程L的距離。

1.2.2 改進啟發信息函數

傳統蟻群算法的啟發信息函數ηij與柵格i和柵格j之間的距離成反比，但相鄰柵格之間的距離差異很小，對路徑搜索的引導作用不大。目前，對有效的改進是將螞蟻下一可選柵格到終點的距離與當前柵格到下一可選柵格的距離的加權和倒數作為啟發信息函數[14]。該方法雖然考慮當前柵格轉移到下一柵格所付出的代價，但相鄰柵格距離差異較小，對整體的啟發信息影響也不大。為此，本文引入放大系數A來增大相鄰柵格的啟發信息差異，從而增大螞蟻選擇更短節點的概率。

式中，ηij為啟發信息函數，表示螞蟻從節點i轉移到節點j的期望程度；dij為節點i到下一節點j的歐氏距離；djE為下一節點j到目標節點E的歐式距離；A為放大系數；μ為常數。

1.2.3 改進信息素更新規則

傳統蟻群算法采用全局信息素更新方式，只有最短路徑上信息素被更新，雖然可以很好地利用最優解信息，但蟻群會過早集中在同一條路徑上，降低算法的全局搜索能力，易陷入局部最優解。另外，在更新最短路徑上的信息素時，很少有人考慮到最短路徑可能并非只有一條，大多只更新其中一條最短路徑上信息素，可能會丟失最優解（本文定義的最優解為路徑長度最短，轉彎次數最少的路徑）。針對上述問題，本文提出所有到達終點的路徑都進行信息素更新，并找到所有的最短路徑，然后在額外獎勵最優路徑時首次引入轉彎次數影響因素（轉彎次數的增加會大大降低AGV運行時的工作效率，過于頻繁地轉向還會加速AGV的損耗，縮短使用壽命），選擇轉彎次數最少的最短路徑作為最優路徑更新信息素，從而得到平滑度更高，更符合AGV運行特征的路徑。改進后的信息素更新公式為：

式中，ρ為信息素揮發系數，0＜ρ≤1；τij表示t時刻信息素；Δτij為信息素增量，初始時刻Δτij=0；Q為信息素總量；Δτbestij為最優路徑上的信息素增量；Lm為到達終點的路徑長度；Lbest為最優路徑長度。

2 動態窗口法及改進

2.1 動態窗口法基本原理

動態窗口法[15]是在充分考慮到AGV自身機械特性限制以及環境對速度的約束下，在速度二維空間中采樣多組速度對（線速度、角速度），在一定時間間隔內同時模擬AGV在這些速度對下的軌跡。獲取多組可行模擬軌跡后，根據設計的評價函數，AGV以最優模擬軌跡所對應的速度對，完成局部路徑規劃。

2.1.1 速度組采樣

在速度空間中存在無窮多組速度對(v,ω)，根據AGV自身限制及環境因素，對采樣速度范圍進行約束：

（1）速度約束

設AGV初始狀態下的速度為Vs，則：

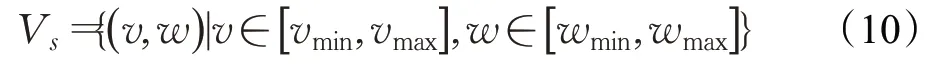
式中，v、w分別表示速度和角速度；vmin、vmax和wmin、wmax分別表示速度和加速度最小值與最大值。

（2）最大加速度約束

由于電機力矩有限，存在最大加速度限制，因此使得AGV軌跡的前向模擬周期內，存在一個動態窗口vd，該窗口的速度集合是AGV在下一個時間間隔內實際能夠達到的速度，則：

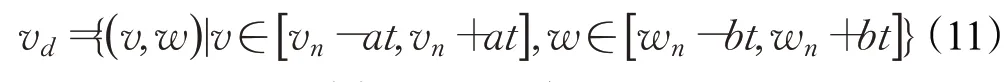
式中，vn、wn分別表示AGV當前狀態下的速度與角速度；a、b分別表示AGV的加速度與角加速度。

（3）制動距離約束

為保證AGV的運行安全，在最大減速度下，當前速度應能在撞到障礙物前減速為0，即：

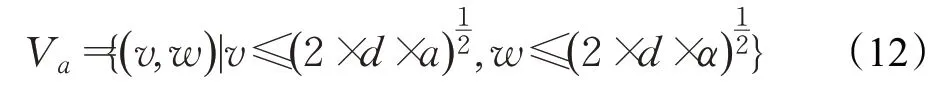
式中，d為速度(v,w)對應軌跡終點到障礙物最近的距離。

2.1.2 設計評價函數

動態窗口法評價函數設計準則是AGV盡量避開障礙物，朝向目標快速前進。設計的評價函數為：

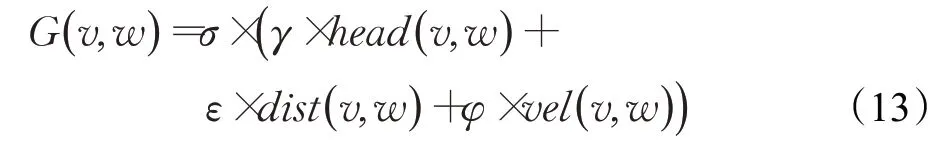
式中，head( v,w)為方向角評價子函數，表示在當前速度下，模擬軌跡終點方向與目標點之間的方向角偏差；dist( v,w)為距離評價子函數，表示在當前速度下，模擬軌跡終點到障礙物最近的距離；vel( v,w)為當前速度大小評價子函數；σ為平滑函數；γ、ε、φ為各評價子函數加權系數。

2.2 改進動態窗口法

2.2.1 改進距離評價子函數dist( v,w)

傳統距離評價子函數dist(v,w)，并未考慮模擬軌跡其余點到障礙物的距離，這可能會出現模擬軌跡終點繞開了移動障礙物，但軌跡上的其余點與移動障礙物發生了碰撞的情況，如圖1所示。針對這種情況，本文提出了改進的距離評價子函數，以模擬軌跡上所有點到障礙物的最小距離為評價距離，di st越大，表示AGV離障礙物越遠。

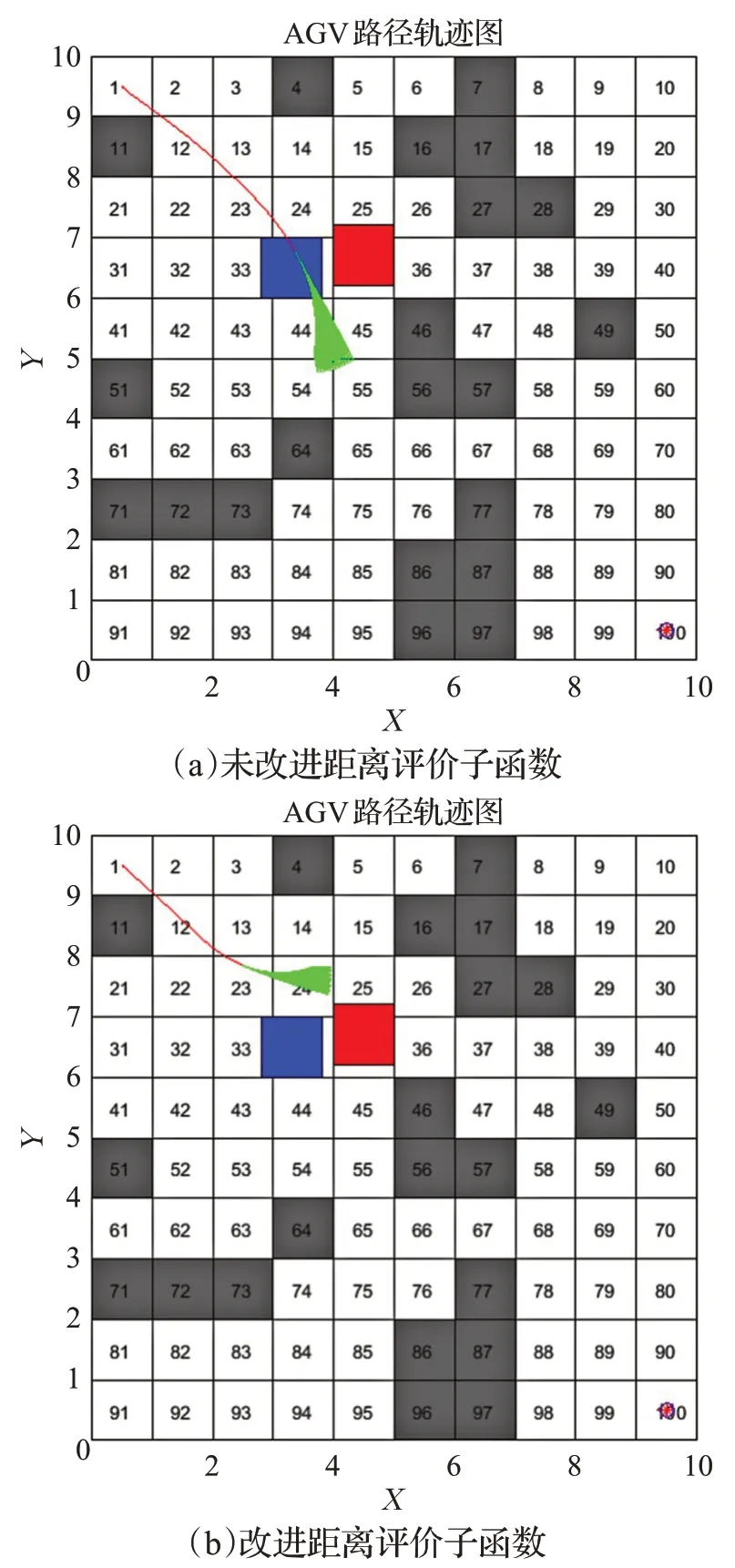
圖1 距離評價子函數的影響Fig.1 Influence of distance evaluation sub-function

2.2.2 動態設定AGV初始狀態航向角

AGV初始航向角是隨機設定的固定角，當與目標點角度偏差較大時，會出現初期搜索路線繞行的現象，增加AGV運行路徑的冗余，如圖2所示。因此，本文提出了以起點與第一個子目標點的連線與水平方向的夾角來動態設定AGV初始航向角，明確搜索路徑的前進方向，避免繞行。

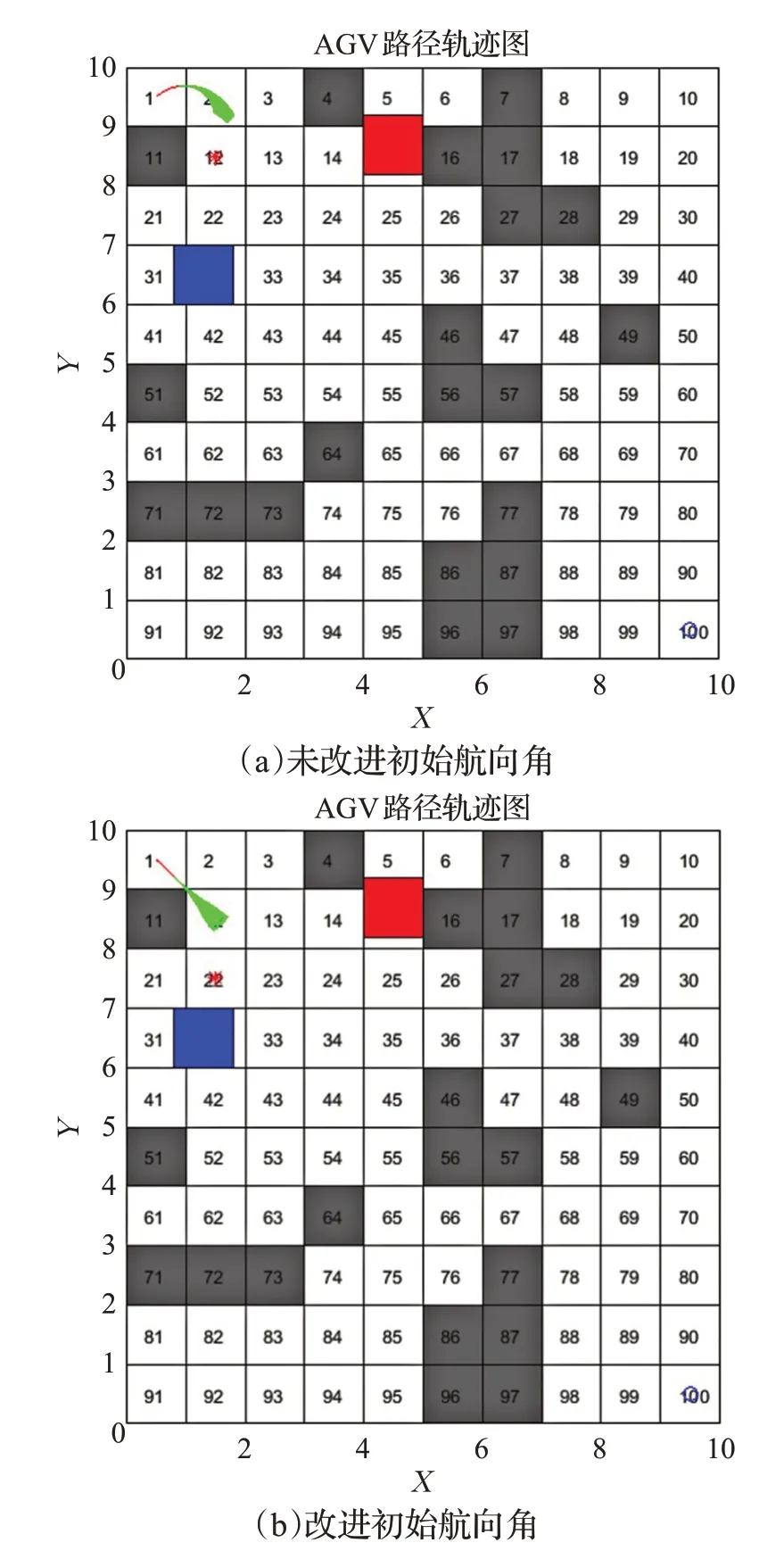
圖2 初始航向角的影響Fig.2 Influence of initial heading angle

設起點坐標為(XS,YS)，第一個子目標點的坐標為(X1,Y1)，則AGV的初始航向角φ為：

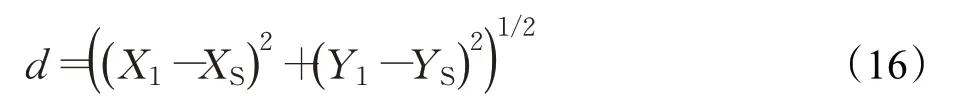
式中，c為初始航向角的正弦值；d為起點與第一個子目標點的歐式距離。

2.3 全局動態路徑規劃算法

動態窗口法根據AGV檢測到的局部環境信息，實時動態規劃路徑，具有良好的避障能力，但由于無法有效利用全局環境信息，存在易陷入局部最優、無法到達目標點等致命問題。因此，本文提出利用改進蟻群算法進行全局靜態路徑規劃，然后將規劃的最優路徑上各轉折點依次作為改進動態窗口法的子目標點，終點為總目標點，分步指引動態窗口法沿全局最優路徑方向進行實時動態路徑規劃，以保證動態規劃路徑的全局最優性。若在行程后期出現目標位置轉移的情況，可以根據目標點轉移狀態分為兩種情況：（1）若目標點一直移動，則可以利用改進的動態窗口法動態追蹤移動目標點，但路徑質量可能較差；（2）若目標點轉移后靜止不動，則可以將當前位置設為起點，轉移后的目標位置設為終點，重新調用全局動態路徑規劃算法進行實時動態路徑規劃。這里僅簡單討論兩種目標轉移情況的解決方法，在下文實驗中并不考慮目標轉移的情況，因此全局動態路徑規劃算法的具體流程如圖3所示。

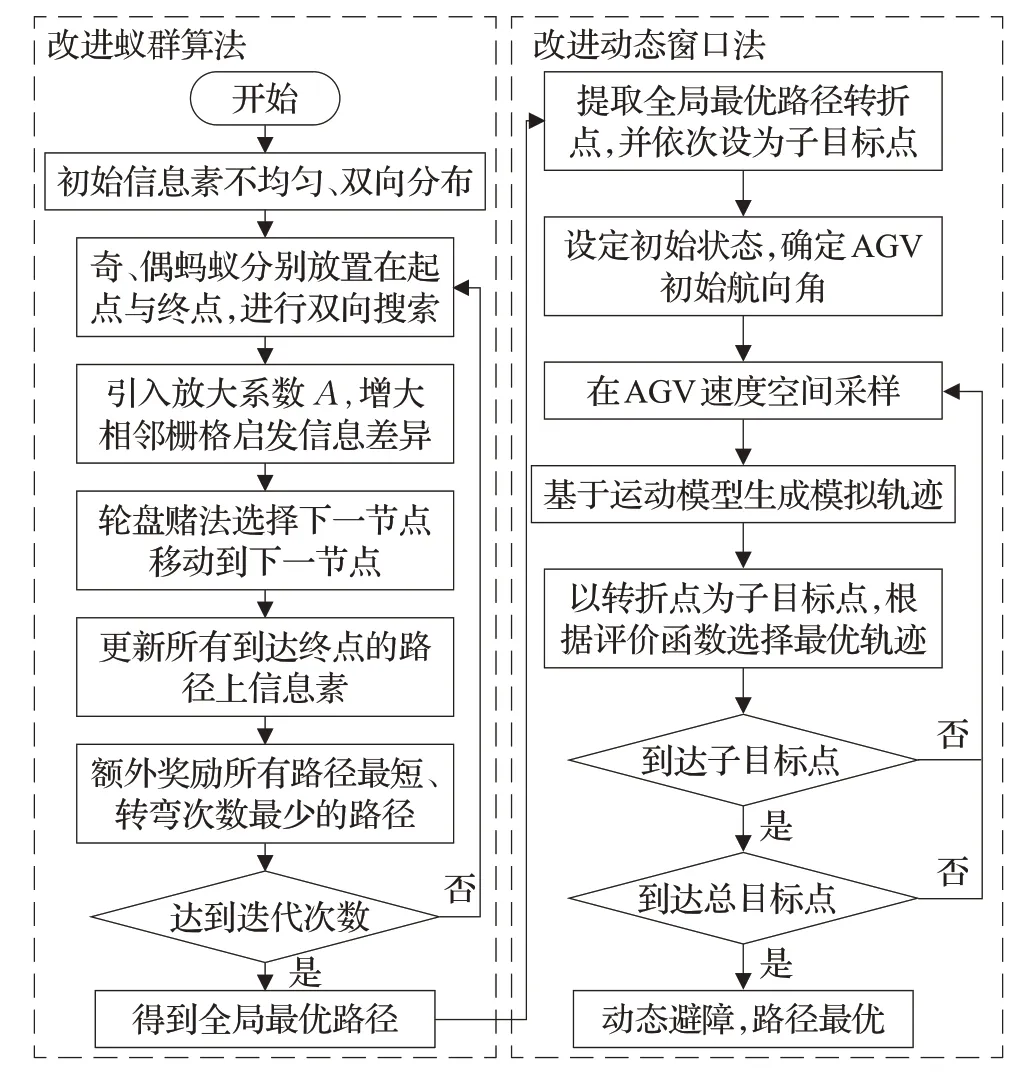
圖3 全局動態路徑規劃算法流程圖Fig.3 Flow chart of global dynamic path planning algorithm

3 仿真實驗

3.1 基于改進蟻群算法的全局靜態路徑規劃

為了驗證改進蟻群算法的可行性和有效性，本文利用編碼簡單、易于實現的柵格地圖法建立模擬環境[10]，在不同模擬環境下，通過Matlab進行傳統蟻群算法和本文改進蟻群算法的仿真實驗對比。相關實驗數據如下：迭代次數K=100，螞蟻數量M=50，信息素啟發因子α=1，期望啟發因子β=8，信息素揮發系數ρ=0.4，信息素增量Q=10。

（1）仿真實驗環境一（圖4～圖6）

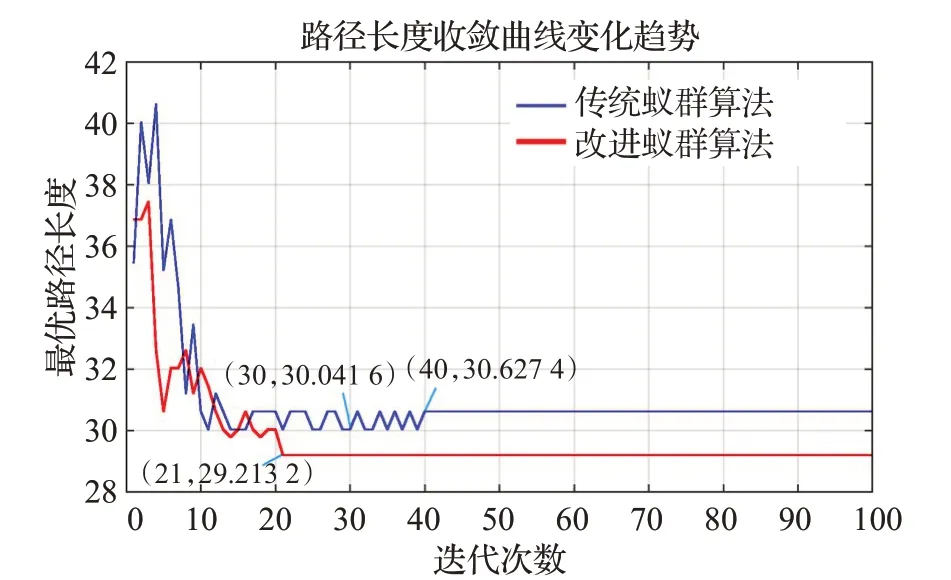
圖4 傳統與改進蟻群算法的路徑長度收斂對比（實驗1）Fig.4 Comparison of path length convergence between traditional and improved ant colony algorithms（E1）

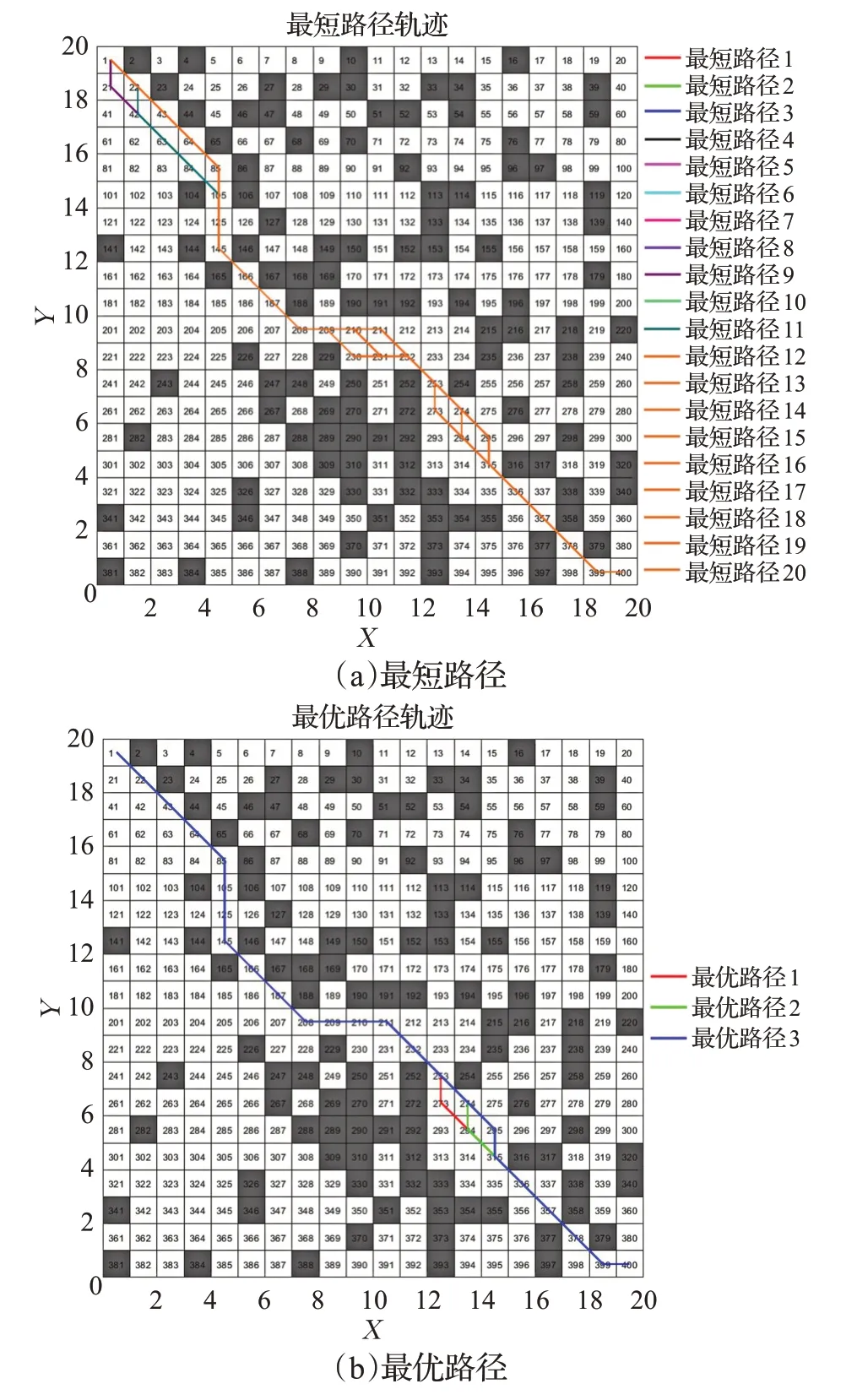
圖6 改進蟻群算法路徑軌跡（實驗1）Fig.6 Path trajectory of improved ant colony algorithm（E1）

仿真實驗環境一是規模為20×20的二維平面，可移動柵格與障礙物柵格比為7∶3，障礙物隨機分布。

（b）仿真實驗環境二（圖7～圖9）

仿真實驗環境二是規模為30×30的二維平面，可移動柵格與障礙物柵格比為7∶3，障礙物隨機分布。

圖4～圖9是分別是不同環境下傳統蟻群算法和本文改進蟻群算法運行10次中規劃效果最好的結果，表1是不同實驗環境下兩種算法搜索結果對比。圖4、圖7中藍線表示傳統蟻群算法的路徑長度收斂曲線，紅線表示本文改進蟻群算法的路徑長度收斂曲線；圖5、圖6、圖8、圖9分別是傳統蟻群算法和本文改進蟻群算法在不同仿真實驗環境中搜索的所有最短路徑和最優路徑（即路徑最短，轉彎次數最少）。由表1可知，在仿真實驗環境一中，本文改進蟻群算法與傳統蟻群算法相比：最優路徑長度減少2.8%，轉彎次數減少25%，迭代次數減少47.5%；在仿真實驗環境二中，本文改進蟻群算法與傳統蟻群算法相比：最優路徑長度減少4.9%，轉彎次數減少38.5%，迭代次數減少55%。

圖5 傳統蟻群算法路徑軌跡（實驗1）Fig.5 Path trajectory of traditional ant colony algorithm（E1）

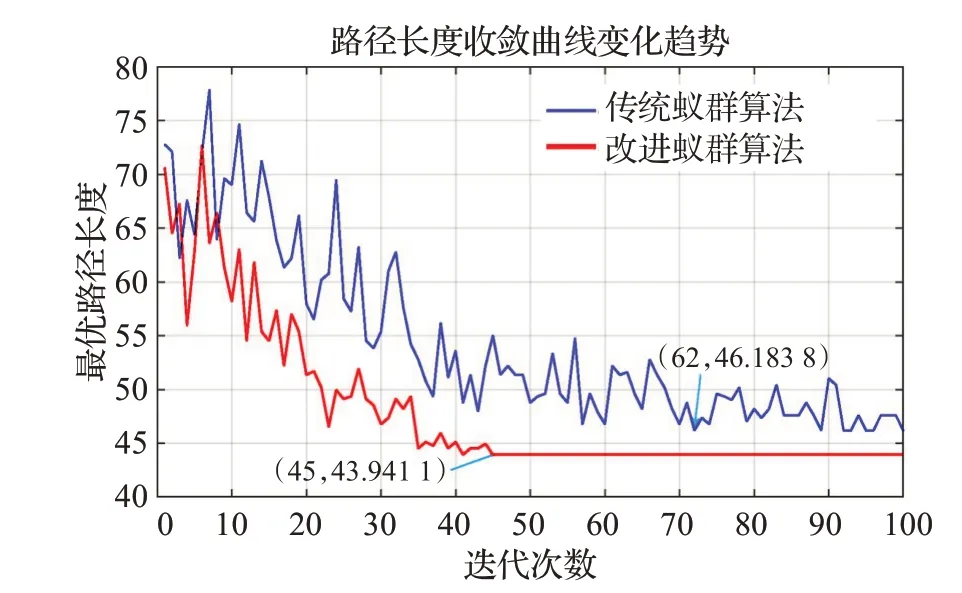
圖7 傳統與改進蟻群算法的路徑長度收斂對比（實驗2）Fig.7 Comparison of path length convergence between traditional and improved ant colony algorithms（E2）

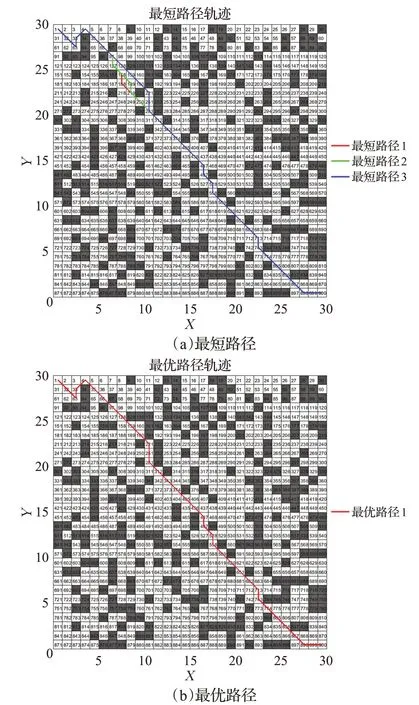
圖8 傳統蟻群算法路徑軌跡（實驗2）Fig.8 Path trajectory of traditional ant colony algorithm（E2）

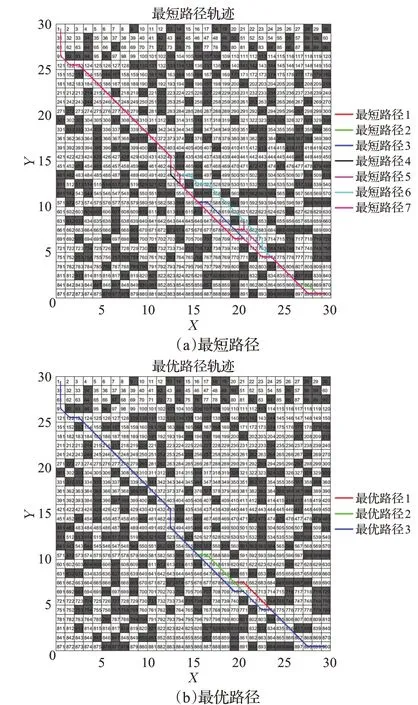
圖9 改進蟻群算法路徑軌跡（實驗2）Fig.9 Path trajectory of improved ant colony algorithm（E2）

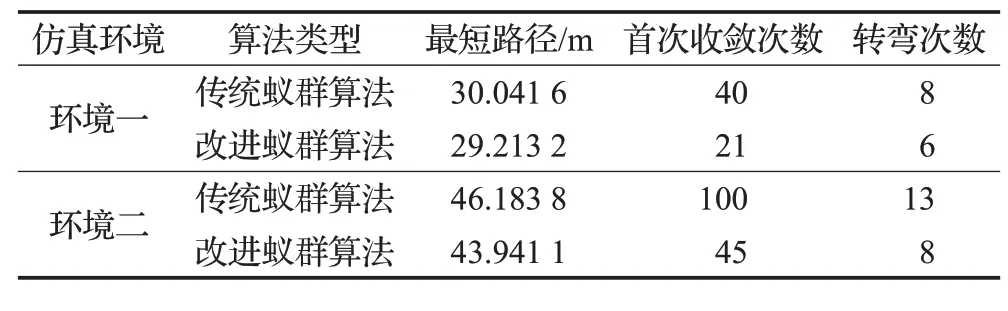
表1 不同實驗環境下兩種算法搜索結果對比Table 1 Comparison of search results of two algorithms in different experimental environments

通過不同環境下的仿真實驗可知，本文提出的改進蟻群算法收斂性更好，規劃的全局最優路徑質量更優、平滑度更高，證明了本文改進蟻群算法的可行性和有效性。

3.2 基于全局動態路徑規劃算法的實時路徑規劃

為了驗證全局動態路徑規劃算法的可行性和有效性，本文在不同模擬環境下，通過Matlab進行傳統動態窗口法和本文提出的全局動態路徑規劃算法仿真實驗對比。改進蟻群算法的相關數據參考3.1節；改進動態窗口法的相關數據如下：AGV最高線速度1.0 m/s，最高角速度30.0（°）/s，加速度0.2 m/s，旋轉加速度60.0（°）/s，線速度分辨率0.01 m/s，角速度分辨率1.0（°）/s，航向得分的比重0.4、距離得分的比重0.4、速度得分的比重0.2、向前模擬軌跡的時間3 s，距離目標點的距離小于0.5 m時，則認為AGV到達目標點。

（1）仿真實驗環境一

仿真實驗環境一是規模為10×10的二維平面，可移動柵格與障礙物柵格比為8∶2，障礙物隨機分布。本文在柵格地圖中設置了兩個移動障礙物：紅色柵格設為動態障礙物A，藍色柵格為動態障礙物B。

（2）仿真實驗環境二

仿真實驗環境二是規模為20×20的二維平面，可移動柵格與障礙物柵格比為8∶2，障礙物隨機分布。由仿真實驗環境一可知傳統動態窗口法在相對簡單環境下無法找到目標點，所以本次實驗僅做了全局動態路徑規劃算法。

圖10分別表示AGV從遇到動態障礙物B到有效避開動態障礙物B的全過程。圖11、圖12、圖13分別表示傳統動態窗口法和本文改進的全局路徑規劃算法的路徑軌跡，其中，圖12（a）、圖13（a）為全局動態路徑規劃算法動態路徑規劃軌跡，圖12（b）、圖13（b）為改進蟻群算法規劃的全局最優路徑（紅線）與全局動態路徑規劃算法規劃的全局最優路徑（藍線）的對比。由圖11可知，傳統動態窗口法雖然可以有效躲避移動障礙物，但由于缺少全局信息的指導，陷入死鎖，無法成功到達目標點。由圖12（a）、圖13（a）可知，在全局信息的指導下，本文提出的全局動態路徑規劃算法可以有效躲避動態障礙物的同時規劃出全局最優路徑；由圖12（b）、圖13（b）可知，與改進蟻群算法相比，全局動態路徑規劃算法規劃的路徑曲率連續，平滑度更高，更適合AGV的高效運行。

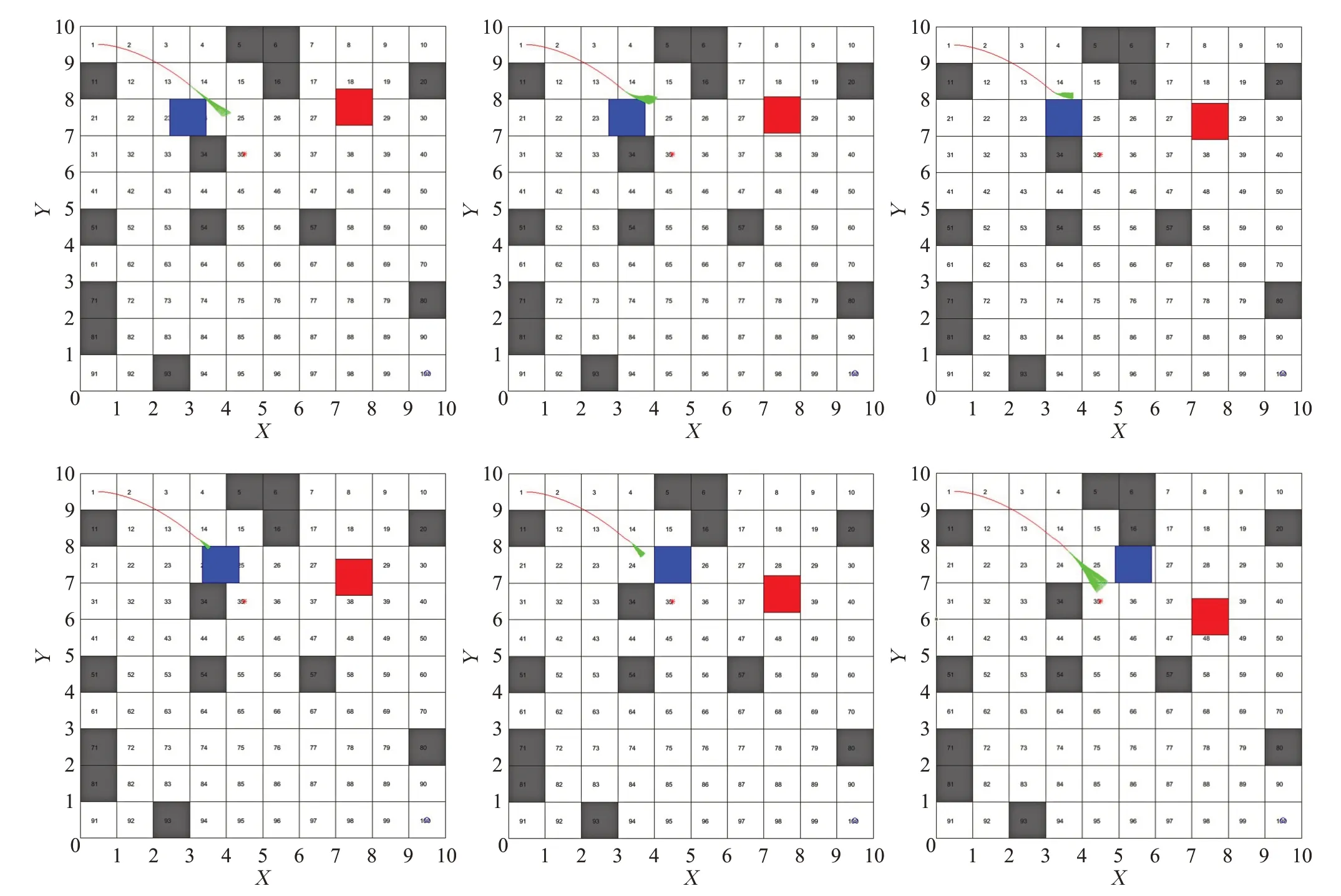
圖10 動態躲避障礙物過程Fig.10 Dynamic avoidance of obstacles process

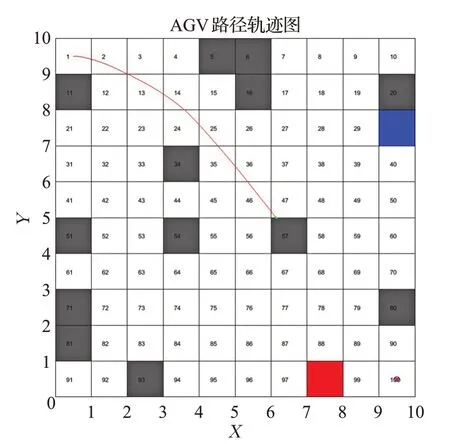
圖11 傳統動態窗口法Fig.11 Traditional dynamic window approach

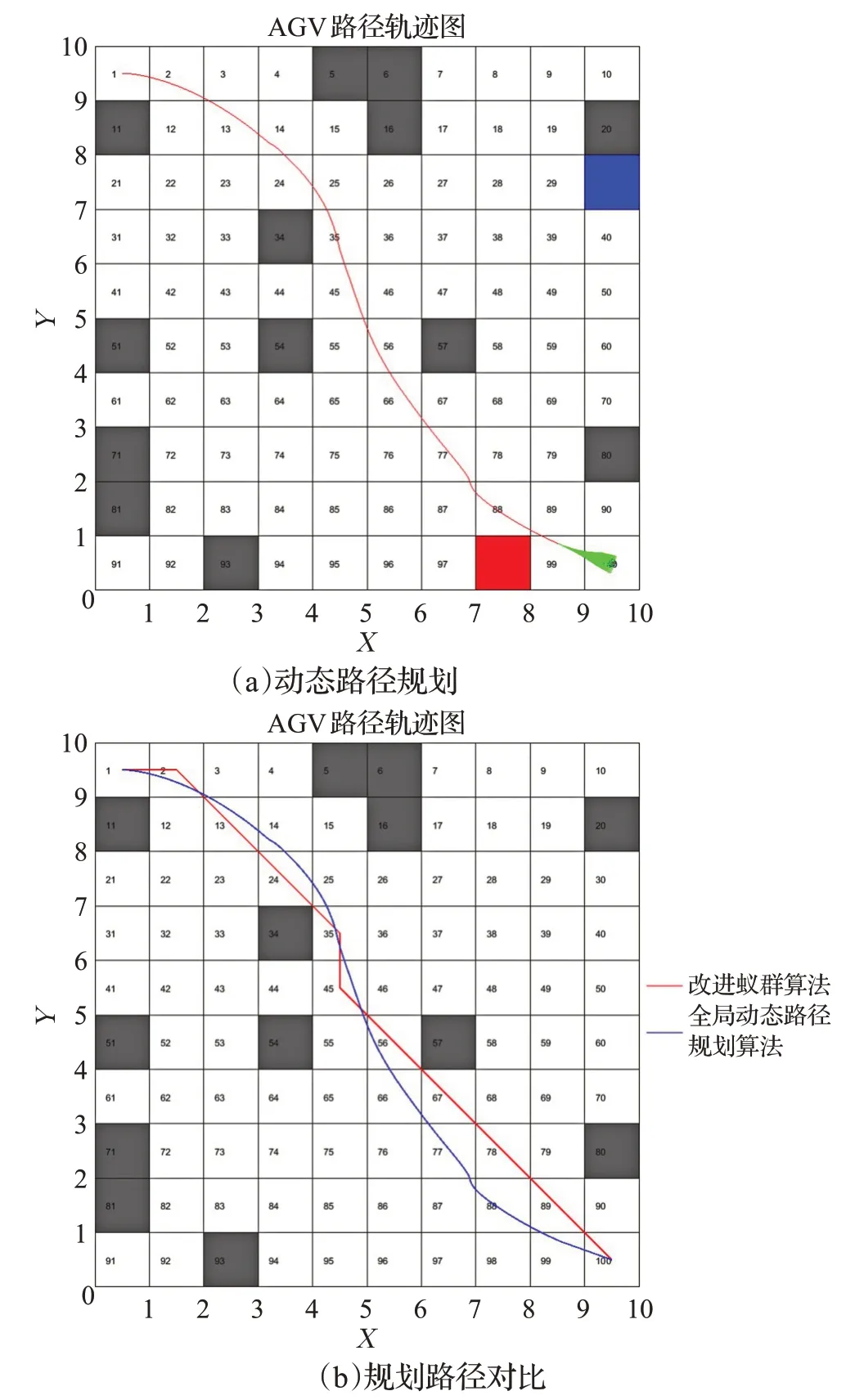
圖12 改進的全局動態路徑規劃算法（實驗1）Fig.12 Improved global dynamic path planning algorithm（E1）

圖13 改進的全局動態路徑規劃算法（實驗2）Fig.13 Improved global dynamic path planning algorithm（E2）

通過不同環境下仿真實驗可知，在全局信息的指導下，本文提出的全局動態路徑規劃算法在不同環境下都可以通過實時動態路徑規劃躲避動態障礙物，規劃出全局最優路徑，證明了本文提出的全局動態路徑規劃算法的可行性和有效性。

4 結束語

針對全局靜態路徑規劃算法無法有效躲避動態障礙物、局部動態路徑規劃算法缺少全局環境信息而易陷入局部最優或無法到達目標點等問題，本文提出了一種結合改進蟻群算法和動態窗口法的AGV全局動態路徑規劃算法。首先，對傳統蟻群算法進行改進：（1）基于雙向搜索策略提出初始信息素不均勻、雙向分布，為蟻群算法雙向搜索提供大體方向，避免算法初期存在盲目搜索、收斂性差等問題；（2）針對相鄰柵格距離差異較小，本文引入放大系數A來增大相鄰柵格的啟發信息差異，增大螞蟻選擇更優節點的概率；（3）更新信息素時引入轉彎次數影響因素，在所有最短路徑中選擇轉彎次數最少的路徑作為最優路徑更新信息素，從而得到更平滑的路徑，提升AGV運行效率。然后，對動態窗口法進行改進：（1）改進距離評價子函數，以模擬軌跡上各點到障礙物最小距離為評價距離，評價距離越大，表示AGV離障礙物越遠，避障效果越好；（2）提出以起點與第一個子目標點的連線與水平方向的夾角動態設置AGV的初始航向角，明確搜索路徑的前進方向，避免初始航向角設置不當造成繞行。最后，結合改進的蟻群算法和動態窗口法構建全局動態路徑規劃算法，以改進蟻群算法規劃的全局最優路徑上各轉折點為動態窗口法子目標點，引導動態窗口法沿著全局最優路徑方向進行實時動態路徑規劃，最終實現AGV在動態環境下沿著全局最優路徑躲避動態障礙物。通過不同環境下的仿真實驗結果，證明了本文提出的改進蟻群算法和全局動態路徑規劃算法均可行和有效。