基于中、短時間尺度的春節負荷特征滾動預測

章 昊

(國網安徽省電力有限公司，安徽 合肥 230022)

負荷預測是根據過去和現在的電力需求推測未來的電力需求。準確的負荷預測，可以經濟合理地安排電網內部發電機組的啟停，合理安排機組檢修計劃，有效降低發電成本，使電網安全穩定地運行，保障社會正常的生產和生活[1]。通常根據區域負荷的組成、生產生活規律等歷史信息進行預測。預測可以分為超短期、短期、中期和長期負荷預測[2]，分別用于預測未來分鐘至小時、日至周、月至年、若干年的負荷情況，為預防緊急狀態、日/周調度計劃、運行方式/檢修安排、電網改造/擴建規劃提供相應的負荷信息[3]。

文獻[4]提出對GM(l,1)模型進行改進，采用神經網絡與其他理論相結合的方法。生成組合預測模型，用于春節假日負荷的預測，但預測誤差呈現一定隨機性。現代預測方法包括人工神經網絡預測法和模糊預測法[5]。文獻[6]提出了模糊預測理論，并讓其運用于短期負荷預測，但需要運用大量歷史數據進行分析，春節假日過少的樣本數量使其預測具有一定難度[7]。文獻[8]使用移位修正法，對春節負荷及春節效應進行數據修正，但由于模型假定春節效應影響期間用電量保持不變，與實際情況不符合。文獻[9]驗證了春節效應影響時期的設定對于春節效應調整具有較大影響，但缺少對客觀事實的分析，難以研究具體調整的作用機理。

本文主要研究負荷的組成及特征，提出了一種從經濟發展、氣象變化、電力消費結構等方面，對負荷特征提取的方法，預測春節期間日負荷曲線的谷荷、早晚峰荷和腰荷，并基于中、短時間尺度的負荷逐步修正，使預測精度逐步提高。

1 負荷特征

1.1 負荷組成

負荷由工業負荷、農業負荷、商業居民負荷和其他負荷構成。工業負荷主要分為重工業負荷和輕工業負荷，短期內負荷需求較為平穩。

農業負荷主要為農村生產與排灌用電，與季節相關，在冬季可以近似忽略。

商業負荷主要包括與商業運轉相關的負荷。春節假日商業、居民負荷的時間、空間分布規律與周末假日接近，但考慮到春節的民俗特殊性，春節假日地域性人口流動會引起商業、居民負荷的變化。

1.2 氣象特征指標

連續多天的氣溫變化對負荷具有累積效應，通過對不同天數累積效應的對比，采用前5天的氣溫數據進行累積效應分析，確定累積效應的模型最佳參數[10]，設置權重分別為0.55、0.3、0.1、0.04和0.01，計算得到觀察日的累積平均溫度[11]。

人體舒適度是指在不特意采取任何防護措施下，人在自然環境中感覺舒適達到何種程度的描述，以氣溫、濕度和風的影響最為突出[12]，計算公式為

(1)

式中：C為人體舒適度指數；T為氣溫，℃；RH為相對濕度，%；V為風速，m/s。

考察人體舒適度、最高溫度、最低溫度、累積平均溫度、平均溫度等氣象因素對某省(簡稱A省)級電網歷年春節期間日最大負荷的影響，相關性分析如表1所示。

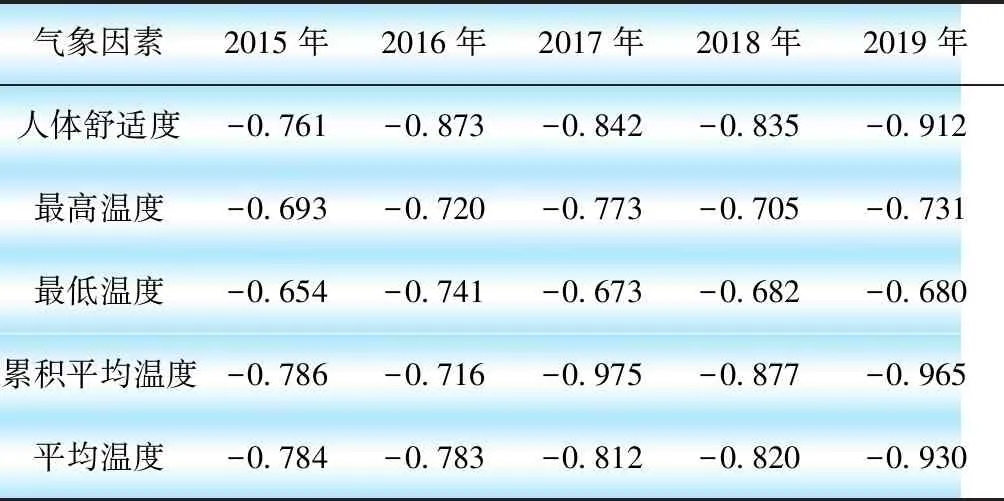
表1 各指標與日最大負荷相關系數

由表1可知，在各種氣象指標中，累積平均溫度與負荷的相關性最強，考慮到信息的耦合性和獲取能力，選擇累積平均溫度為主要的氣象特征指標。以2019年為例，A省春節期間日負荷特征和日累積平均溫度曲線如圖1所示。

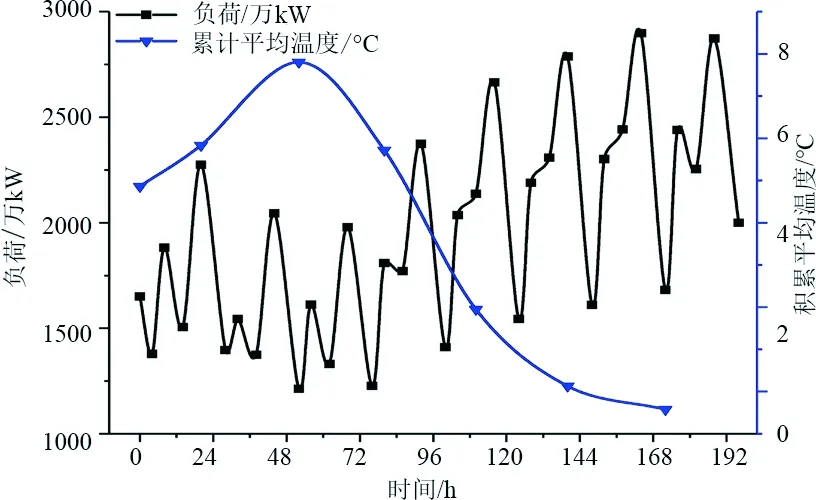
圖1 春節期間日負荷特征和日累積平均溫度關系

選取了谷荷、早高峰負荷、腰荷和晚高峰負荷作為日負荷特征，通過對多年春節負荷數據的觀察，發現A省春節期間日負荷特征和日累積平均溫度滿足負相關關系，其中日最大負荷(即晚高峰負荷)與累積平均溫度的相關性遠大于其他特征量與溫度的相關性，如表2所示。在春節負荷預測中由累積平均溫度去預測日最大負荷會更準確。

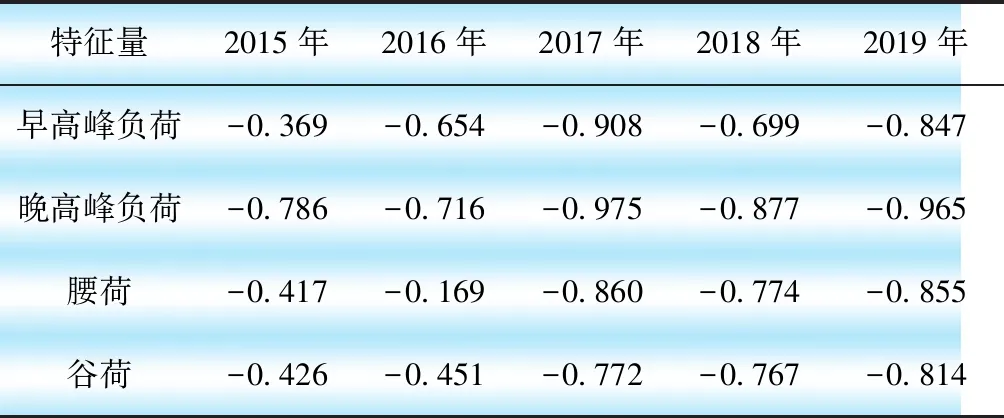
表2 累積平均溫度與各負荷特征的相關性

1.3 春節日負荷特征的關系

以日最大負荷為基準，對當日谷荷、早高峰負荷、腰荷和晚高峰負荷進行標幺。

(2)

式中：pi,k為第i日第k個日負荷特征,Pi,k占當日最大負荷Pi,max的百分比；k為1,2,3,4時，Pi,k分別對應于第i日的谷荷、早高峰負荷、腰荷和晚高峰負荷，Pi,max=max{Pi,1,Pi,2,Pi,3,Pi,4}。

定義n日內的平均日負荷特征。

(3)

A省各年春節期間平均日負荷特征見圖2。

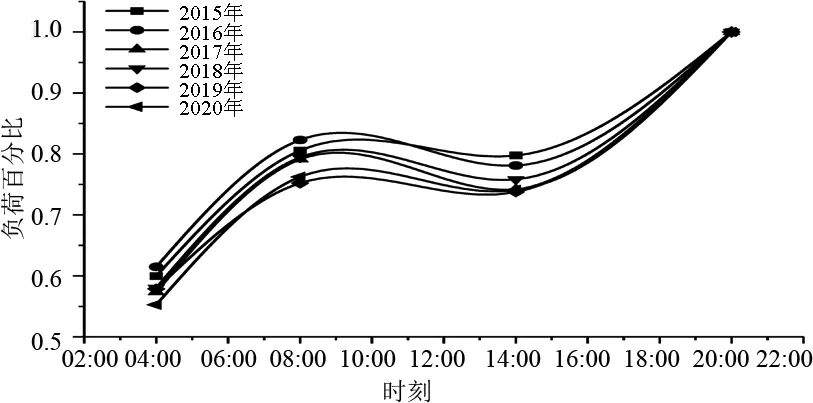
圖2 春節期間平均日負荷特征

圖2中春節期間的平均日負荷特征分布在各年都比較接近，說明春節期間的負荷組成基本固定，如已知某一個日負荷特征(如晚高峰負荷)，就可以推得其他負荷特征。

春節對應日晚高峰負荷的逐年對比如圖3所示，由圖3可知：①日最大負荷逐年穩步增長，考慮是因經濟發展引起的負荷增長；②對于春節期間溫度較為均衡年份，總體呈現春節后幾日的日最大負荷大于前幾日，最后一日負荷大于其他幾日的規律，考慮是因假期結束人群返崗所致。2016年春節后幾天溫度明顯高于春節平均溫度，使2016年春節最后幾日日最大負荷較低。2020年較為特殊，不具普遍性。因此無法對春節的日最大負荷進行整體分析，必須逐日具體分析計算。

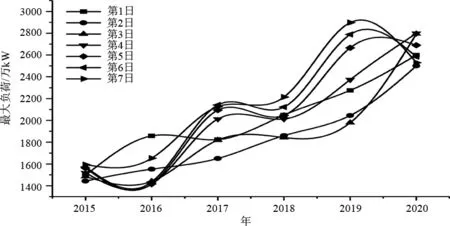
圖3 春節對應日晚高峰負荷的逐年對比

1.4 假日屬性對負荷特征的影響

定義第i天的日氣象特征向量為

Ti=|Ti,a,Ti,max,Ti,min|

(4)

式中：Ti,a為第i天的日累積平均溫度；Ti,max為第i天的日最高溫度；Ti,min為第i天的日最低溫度。

以第i天的氣象條件為基準，根據日氣象特征向量定義相似時段內第j天與第i天的氣象特征差異度為

φij=[ra(Ti,a-Tj,a)+rmax(Ti,max-Tj,max)+rmin(Ti,min-Tj,min)]

(5)

式中：ra、rmax、rmin分別為相似時段內的日累積平均溫度、日最高溫度、日最低溫度與第i天日最大負荷的相關系數。

做出A省2019年春節各日與其氣象相似周末的日負荷特征，如圖4所示。春節與氣象相似周末的日負荷分布規律具有很高的相似性，其差異主要體現為春節與周末負荷除去氣象因素影響的節假日特殊性。另外，各日特征相似度會隨春節假日日期的變化而變化，說明春節期間各日負荷的組成會改變。

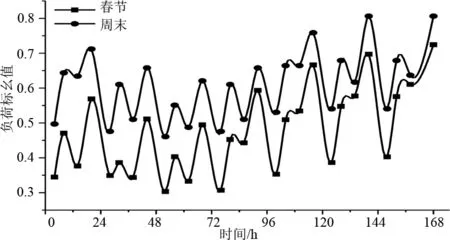
圖4 春節與相似周末負荷對比

2 春節負荷滾動預測方法

對利用歷史數據對A省春節負荷的分布規律分析后，建立春節各日最大負荷不同時間尺度的滾動預測方法，并建立兼顧中、短時間尺度預測的春節各日負荷特征預測方法。

時間尺度預測中，已知待預測春節前一年的負荷。在氣象條件相似的情況下，春節前周末與春節期間各日的負荷特征分布相似，利用春節前周末負荷去預測春節負荷，包括基礎負荷和與氣象有關的氣象負荷兩部分：①根據待預測地區的氣象特點，將不需要投入制冷或制熱負荷時段內(如4、5月份)周末日最大負荷的平均值確定為當月的基礎負荷。認為基礎負荷與一個地區的經濟發展水平相關；②根據歷年基礎負荷數據，計算基礎負荷的年增長率，并進一步得到其月增長率，計算待預測春節當月的基礎負荷。

確定待預測地區春節期間的累積平均溫度變化范圍，選取溫度屬于該范圍內的歷史周末，將其最大負荷減去其周末基礎負荷定義為氣象負荷。

在累積平均溫度變化范圍內，建立累積平均溫度與氣象負荷的數學模型。根據累積平均溫度的預測值計算春節前周末假日的氣象負荷。為了進一步顯現其分布規律，將同屬一個累積平均溫度區間的數據點進行聚類，分別計算屬于該區間內數據的累積平均溫度和氣象負荷的平均值，作為該區間所有數據的聚類中心，由此，可以將累積平均溫度與氣象負荷分布圖進行轉化，根據散點圖建立氣象負荷模型。最后綜合基礎負荷與氣象負荷，得到春節前周末假日負荷。

定義R2表示預測值與對應實際數據之間的擬合度，計算公式如下。

(6)

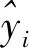
基于已知的歷年春節前氣象條件相似的周末負荷，將周末最大負荷減去春節最大負荷，得到修正量，挖掘其中變化規律。從而根據春節前周末假日負荷預測春節各日最大負荷。

短時間尺度預測中，已知待預測春節前一個月的負荷。基于與待預測春節氣象相似的節前周末實測負荷對春節各日最大負荷進行預測，并利用修正量直接進行春節各日最大負荷的預測。

為了保證預測模型的可靠性，進一步將分別由中、短時間尺度計算得到的春節假日最大負荷，根據加權計算得到最終春節各日負荷預測結果。其中，權重系數結合歷史負荷數據與基于上述方法計算的預測數據擬合得到。

工業負荷短期內負荷需求較為平穩，對應隨經濟增長的基礎負荷部分；農業負荷在冬季可以近似忽略，據此排除這個影響因素；商業負荷、居民負荷對應隨累積平均溫度變化的氣象負荷部分。

由于氣象預報存在偏差，需要預測一定溫度范圍內的負荷數據。該模型得到的是春節假日期間，每日不同累積平均溫度下的最大負荷。其具體模型如下：

(7)

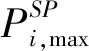
3 算例分析

對于A省電網，已知歷年負荷特征，用2018年及之前的負荷特征數據預測2019年負荷特征數據，驗證預測方法的可靠性。

3.1 春節負荷中時間尺度預測

3.1.1 基礎負荷預測

根據歷年周末基礎負荷數據計算年增長率，得到2019年基礎負荷，如表5所示。周末基礎負荷呈現上升趨勢，歷年增長率的平均值為6.85%，進一步得到月增長率為0.57%。

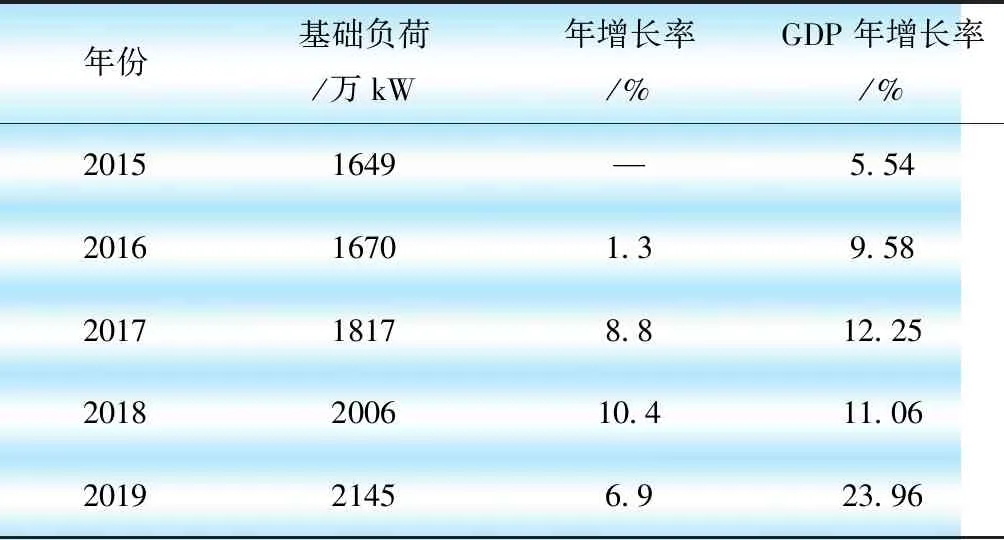
表5 A省歷年周末假日基礎負荷

3.1.2 氣象負荷預測

A省春節期間累積平均溫度范圍為-2～11 ℃，在2018年冬季選取該范圍內的周末假日，用周末假日最大負荷減去周末基礎負荷得到各年的氣象負荷分布規律,如圖5所示。圖5中溫度-氣象負荷數據按照各月實際溫度散布于一個帶狀區域內，溫度與負荷呈近似的反比關系。將同屬1 ℃的累積平均溫度區間的數據點進行聚類，分別計算屬于該區間內數據的累積平均溫度和氣象負荷的平均值，由此圖5可轉化為圖6。

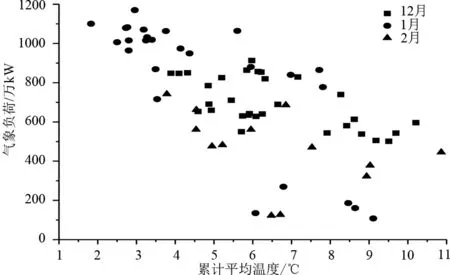
圖5 冬季累積平均溫度與氣象負荷

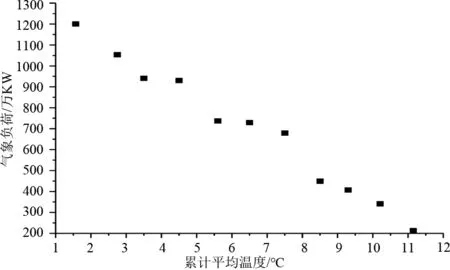
圖6 冬季累積平均溫度與聚類氣象負荷

利用2018年冬季累積平均溫度與氣象負荷數據進行參數擬合，得到Pm=-55.774Ta+879.43，R2為0.9479。

3.1.3 周末-春節效應修正

與春節氣象相似的周末假日最大負荷減去春節假日最大負荷，得到當年春節假日每一天的周末-春節效應修正量。分別識別2015—2018年春節各日在當季的氣象相似周末，并計算出各日的周末-春節效應修正量，如圖7所示。由圖7可知，歷年的春節各日與鄰近的氣象相似周末假日的負荷修正量隨假日的分布類似。可以用各日歷年修正量的平均值作為春節期間每日的周末-春節修正量。

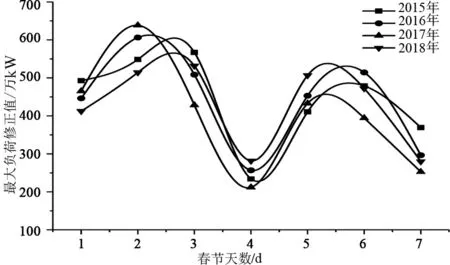
圖7 各年春節期間周末-春節修正量

3.2 計及不同時間尺度的A省春節負荷校驗

為校驗本文提出的負荷預測方法的可靠性與準確性，對2019年春節假日負荷進行了中、短時間尺度預測，并進行加權計算得到最大負荷。最大負荷預測結果分別乘各自比例得到對應日的低谷、早峰、腰荷。預測結果如表6所示。

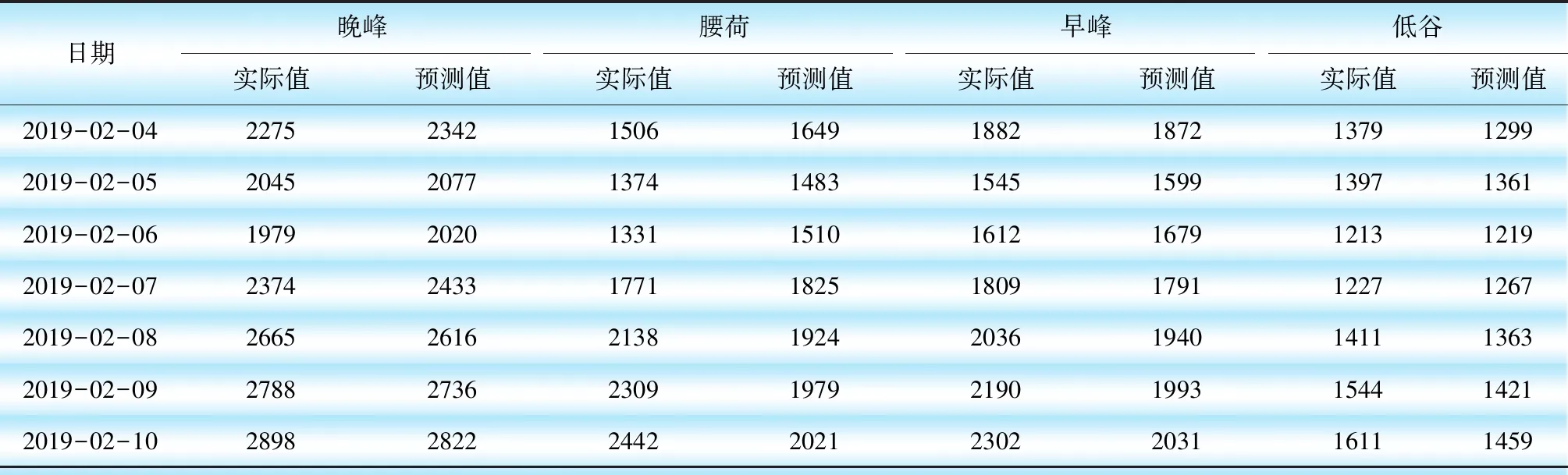
表6 計及中、短時間信息的2019年春節假日負荷預測結果 單位：萬kW

2019年春節各日最大負荷(晚高峰)的預測誤差如圖8所示。由圖8可知，各日的中時間尺度預測、短時間尺度預測、上述兩者加權預測的誤差逐漸減小。負荷預測結果中，低谷、早峰、腰荷、晚峰的預測平均誤差分別為4.96%、4.87%、8.21%、2.21%，晚峰負荷預測最準確，腰荷預測誤差最大。

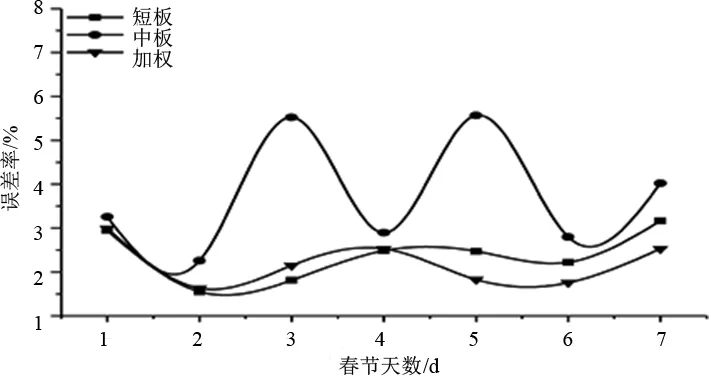
圖8 2019年春節假日負荷預測結果誤差

4 結語

研究春節負荷預測問題對于保證春節期間正常用電具有重要意義。本文預測春節期間日負荷曲線的谷荷、早晚峰荷和腰荷，該方法應用到歷史春節的預測中，從長時間尺度預測、中時間尺度預測、短時間尺度預測以及上述兩者加權預測的誤差逐漸減小，說明基于更豐富和準確的信息可以減少預測誤差。因特殊事件(如疫情的影響)，2020年春節負荷較往年同氣象條件春節負荷略低，并對未來春節負荷的影響依舊存在，由于類似的樣本過少，特殊事件的影響可能會引起一定的負荷預測誤差。對于可以引起人們生活軌跡巨大變化的重大事件，其對負荷的影響應具體分析，主要依賴于較多的歷史數據及相關的影響機理分析。本文目前僅是基于整體省級電網歷史各日的負荷特征對春節負荷進行預測，為了提高預測精度，需要進一步挖掘轄區內各區域的負荷性質和組成，進行更細致的機理分析。