基于卷積網絡與自適應SVM的齒輪箱故障診斷

段澤森, 郝如江， 張曉鋒， 程 旺， 夏晗鐸

(石家莊鐵道大學機械工程學院，河北 石家莊 050043)

齒輪箱是機械設備中最重要的部件之一，齒輪箱的振動信號中含有豐富的運作狀態信息，從中提取有效的信號并對齒輪箱運行狀態進行故障診斷，可以提高齒輪箱的可靠性。

傳統的機械故障診斷方法現在已經無法滿足實際要求，取而代之的機器學習診斷方式[1]。目前機器學習方法有許多種，但“淺層網絡”模型表達能力有限；深度學習模型利用深層網絡結構對輸入樣本進行了深層次地特征提取，克服了傳統方法的缺陷[2,3]。傳統卷積神經網絡存在對特征信息挖掘不夠深入且效率不高等問題[4]。本文提出卷積神經網絡(CNN)與粒子群(PSO)優化支持向量機(SVM)結合的方法，在故障診斷中取得了不錯的效果。

1 理論基礎

1.1 卷積神經網絡架構

卷積神經網絡結構采用卷積層和池化層交替設置，目的是挖掘深層信息特征，以實現對數據的高層表示[5]。

卷積層主要是進行局部特征提取，卷積運算如式(1)所示。池化層是通過對輸入進來的特征信息進行壓縮等處理，池化層的計算公式如式(2)[6]所示，本文擬采取最大池化方式[7]。

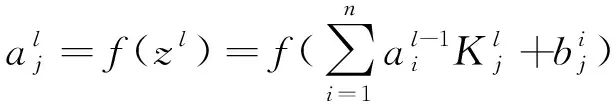
(1)

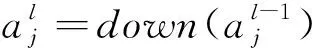
(2)

1.2 支持向量機

支持向量機(SVM)是一種基于統計學理論上的數據挖掘算法，其工作原理是找到一個符合分類需求的最優分類超平面，能夠實現對線性可分數據的最優分類。

本文方法中SVM以RBF(徑向基核函數)為核函數，因其有非常好的分類效果，其中SVM中的懲罰因子C和徑向基核函數內部參數g會直接影響到SVM的分類精度，懲罰因子C主要影響SVM的決策邊界。核函數表達式：

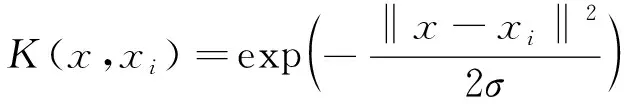
(3)

式中：σ為RBF的寬度參數；exp為以自然常數e為底的指數函數；x-xi為所選取中心點之間的距離。

1.3 粒子群優化的支持向量機

在處理非線性信號時，支持向量機對小樣本分類精度高而且能克服神經網絡中存在的收斂速度慢、過擬合等缺點，但其中核函數參數g和懲罰因子C是影響分類精度的重要參數[8,9]。而粒子群優化算法具有參數少和全局搜索能力強等優點，能夠更快的尋找到支持向量機的最優參數，避免了繁瑣的人工調參。二者結合節省時間的同時，還能有很好的分類效果。為此，本文選用粒子群優化算法對支持向量機進行參數優化。基于粒子群優化的支持向量機全局參數尋優流程如圖1所示。

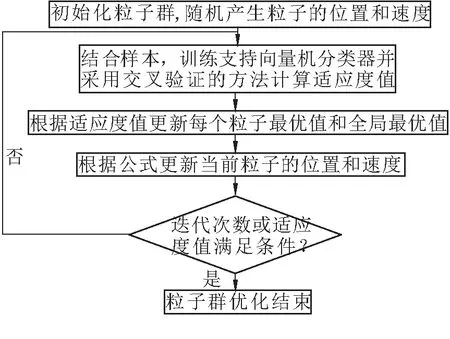
圖1 粒子群(PSO)優化支持向量機(SVM)參數流程

粒子群優化算法(PSO)屬于進化算法的一種，是通過模擬鳥群捕食行為設計的。所有的粒子具有位置x、速度v兩個屬性。PSO初始化為一群隨機粒子，再通過迭代找到最優解。每一次迭代完，粒子會通過追蹤兩個極值來更新自己。一個是粒子自己更新過后的最優值p，另一個是在全局中目前找到的最優值q。粒子通過以下的公式來更新自己的速度和位置：

速度變換公式，

vi+1=wvi+d1r1(pi-xi)+d2r2(qi-xi)(4)

位置變換公式，

xi=xi+vi+1(5)

式中：w為慣性因子；d1,d2分別為學習因子；r1,r2分別為(0,1)之間的隨機數；vi和xi分別為粒子第i維的速度和位置。

2 基于卷積神經網絡與粒子群優化的支持向量機的分類方法

卷積神經網絡(CNN)與粒子群(PSO)優化的支持向量機(SVM)方法主要是把卷積神經網絡原本的Softmax分類器換成了粒子群優化的支持向量機分類器，目的是應用于小樣本中效果好，優化過后的分類器減少尋參時間，提高了網絡模型的訓練效率。本文方法模型為：利用表1、表2，提取數據的時頻特征統計量→時頻特征統計量輸入→卷積層→卷積層→池化層→卷積層→卷積層→池化層→卷積層→卷積層→池化層→卷積層→卷積層→池化層→Dropout層→全連接層→PSO-SVM分類器→輸出層。

表1 時域特征參量

表2 頻域特征參量

3 學習方法的實驗驗證

為了驗證卷積神經網絡與自適應支持向量機方法的可行性，采用美國動力傳動故障診斷綜合實驗臺(DDS)進行實驗驗證，實驗臺如圖2所示。本文設計了10種工況，其中包括1種健康、9種故障類型(滾動軸承內圈故障、外圈故障、滾動體故障、軸承外圈故障+齒輪斷齒故障、齒輪斷齒故障、齒面磨損故障、齒根裂紋故障、齒輪缺齒故障和滾動軸承復合故障)，部分故障類型如圖3所示。

圖2 動力傳動故障診斷綜合實驗臺(DDS)

圖3 齒輪箱零件缺陷

信號采集實驗是在電機恒速下進行，試驗工況：驅動電機轉頻35 Hz; 齒輪箱負載和磁粉制動器負載均為0；采樣頻率 12 800 Hz。每個樣本數據點數20 000，訓練/測試樣本300。

卷積神經網絡與自適應支持向量機方法所建模型的參數設置：卷積層數，8；池化層數，4；卷積核大小，3；池化尺寸，2；Adam優化器，學習率，0.000 5；批處理個數，128；迭代次數，300；Dropout層，0.15。其中粒子群優化算法中的種群數量N=20，學習因子d1=1.8，d2=1.6。

3.1 不同方法分類精度實驗

齒輪箱故障診斷不同學習方法的對比測試結果如表3所示。

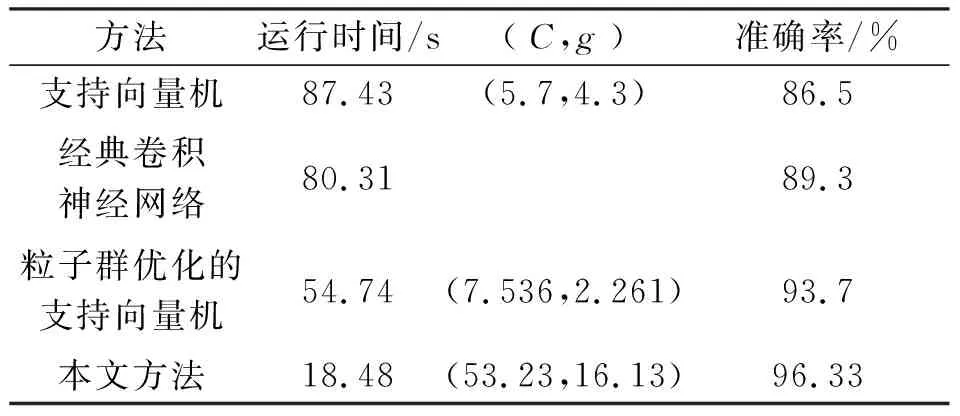
表3 分類器性能對比

對比測試1：使用提取的時頻特征統計量樣本，直接投入到不經過優化的支持向量機中進行分類，實驗結果如圖4所示。

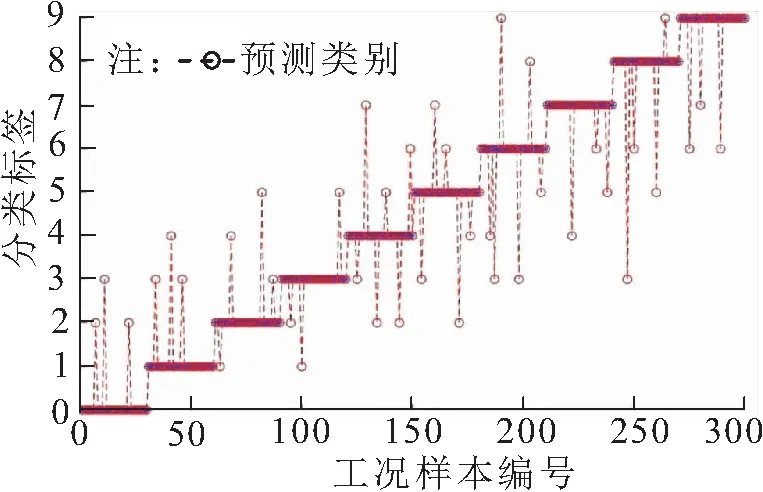
圖4 對比測試1的實驗結果

對比測試2：把提取的時頻特征統計量樣本直接投入到粒子群優化的支持向量機中進行分類，實驗結果如圖5所示。

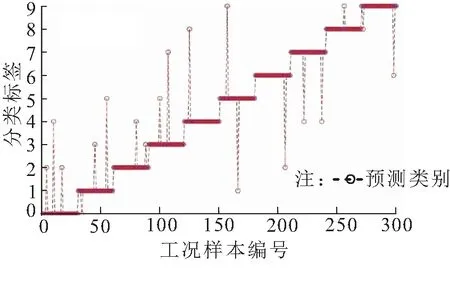
圖5 對比測試2的實驗結果

對比測試3：使用卷積神經網絡對時頻特征統計量進行二次提取，二次提取后的輸出，作為粒子群優化的支持向量機的輸入，進行分類。實驗結果如圖6所示。

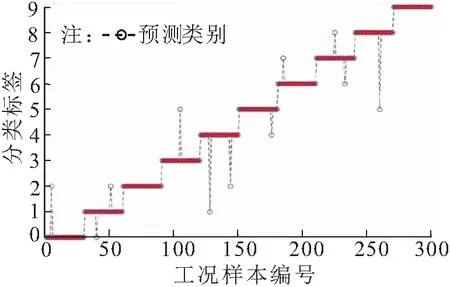
圖6 對比測試3的實驗結果

通過圖4～圖6可知，對比測試1中特征在沒經過優化的支持向量機中，會出現收斂速度慢、分類效果差的問題。對比測試2中缺少卷積神經網絡的二次特征提取，其特征信息不夠好，沒有深度挖掘到有效的特征信息，導致其分類效果差。而對比測試3中本文所建模型，在卷積神經網絡中深層挖掘出有效的特征信息后，輸入到粒子群優化的支持向量機中進行分類，不僅收斂速度快，而且分類效果很好。

從表3可以看出：采用卷積理論與粒子群優化的支持向量機方法齒輪箱故障診斷準確率為96.33%；對比直接用支持向量機分類的方法，準確率提高了9.83%，時間縮短了4.7倍；對比經典卷積神經網絡方法，準確率提高了7%，時間縮短了4倍；對比直接用粒子群優化的支持向量機分類的方法，準確率提高了2.63%，時間縮短了3倍。通過實驗對比，本文提出的方法所得到的效果較好。

3.2 粒子群優化方法適應度實驗

通過100次迭代兩種學習方法的粒子群適應度曲線如圖7所示，對比數據如表4所示。由圖7和表4可知，得出卷積網絡與粒子群優化的支持向量機模型中的粒子浮動小，適應值高，具有很好的適應性。

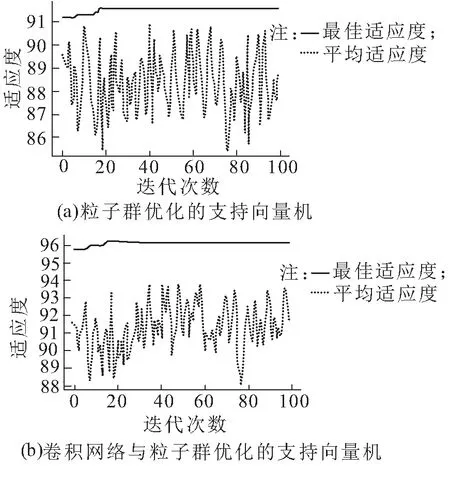
圖7 粒子群適應度曲線

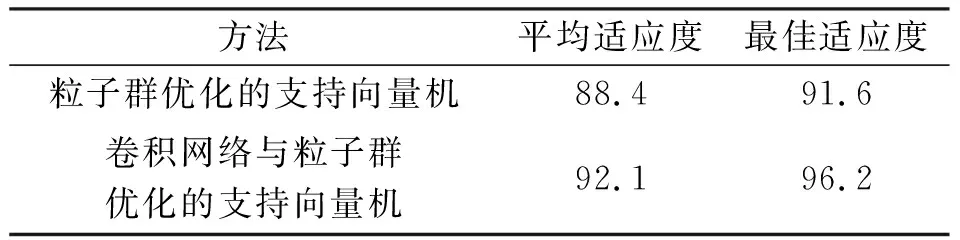
表4 適應度對比 %

4 結論

(1)本文方法能夠有效地提取齒輪箱故障特征，其中通過多層卷積池化和參數尋優，能夠極大提高模型的學習效率。

(2)本文方法采用粒子群優化算法對支持向量機中核函數參數g及懲罰因子C進行優化，利用三種不同方法進行對比，其結果表明本文所建模型的診斷精度高且節省時間。

(3)本文提出模型還存在不足，后續的研究方向是加入混沌搜索，目的是增加粒子群多樣性，避免局部最優，使得網絡模型更加穩定。