基于時頻變換的激波風洞天平信號分析與處理1)

聶少軍 汪運鵬

(中國科學院力學研究所高溫氣體動力學國家重點實驗室,北京 100190)

(中國科學院大學工程科學學院,北京 100049)

引言

近年來,高超聲速技術逐漸受到各個航天大國的深度重視,研究高超聲速技術的相關科學問題具有十分重要的戰略意義[1].在新型高超聲速飛行器氣動外形布局和性能優化中,高溫氣體動力學起到至關重要的作用.通常采用激波風洞開展高焓氣體流動規律研究[2].

激波風洞運行時的有效試驗時間比較短,在極短的時間(毫秒級)內準確測量出飛行器模型的真實氣動力是極具挑戰性的研究課題[3-5].激波風洞天平測力信號(簡稱“風洞測力信號”)不僅包括真實動態氣動力信號,還包括由模型-天平-支撐系統(force measurement system,FMS)慣性振動產生的信號以及其他干擾信號.在進行測力試驗時,模型測力系統受到瞬時沖擊而產生結構振動,這些振動信號在短試驗時間內無法快速衰減,導致測力系統的輸出信號中疊加有慣性振動信號[6].同時,由于模型測力系統結構的復雜性以及受到風洞流場干擾的影響,風洞測力信號中包含的部分高頻率分量(如系統高階模態振動高頻信號、非定常氣動載荷信號等)和流場干擾信號無法在有效試驗時間內衰減到可以忽略的程度,導致無法直接分辨出真實動態氣動力信號的規律性,嚴重影響了測力試驗的精準度.

為了消除風洞測力信號中的慣性干擾,國內外很多學者在改善天平結構方面開展了相關研究,用于發展精準度高、頻率響應快和穩定性強的風洞天平傳感器.其中常見的有脈沖型風洞天平包括壓電天平[7-8]、加速度計天平[9-12]、應力波天平[13-16]、慣性補償型天平[17]以及脈沖型應變天平[18-20]等,上述特種天平技術在激波風洞測力試驗中得到了基于不同程度性能的應用，但仍然無法擺脫慣性振動干擾的影響.有學者將人工智能技術與風洞測力相結合,提出了基于深度學習技術的單矢量動態自校準(single-vector dynamic self-calibration,SVDC)方法并成功應用于脈沖型激波風洞測力系統中,將神經網絡模型應用于激波風洞天平測力信號的智能化處理,得到了較為理想的氣動力載荷信號[21].

目前,通過改善天平結構來提高測量精準度已經非常困難,而且考慮到風洞測力信號比較復雜,不能直接采用傳統的濾波處理或簡單的傅里葉變換(Fourier transform,FT)進行處理.為了成功分辨出風洞測力信號中的真實氣動力信號,本文嘗試尋求新的有效的數據處理方法,對風洞測力信號進行時頻變換分析與處理,從而提升數據處理性能及其應用于工程實際中的可靠性.在時頻處理方法中,選取小波變換(wavelet transform,WT)和希爾伯特-黃變換(Hilbert-Huang transform,HHT)方法,針對尖錐標準模型的風洞測力信號的軸向力信號,開展降噪和時頻變換分析處理,旨在有效辨識出信號中的不同干擾成分,力求輸出可靠的真實氣動載荷信號.為便于數據采集分析,首先在激波風洞外用階躍載荷信號(簡稱“天平階躍信號”)模擬風洞試驗中測力系統受到的激勵作用,用構造的理想階躍載荷信號(簡稱“理想階躍信號”)模擬天平輸出的真實氣動力信號,然后對天平階躍信號進行時頻變換分析處理,用于驗證該時頻方法的可靠性.將WT 和HHT 方法應用于天平階躍信號和風洞測力信號處理,并將處理結果與標準模型結果進行對比分析,為激波風洞天平的高精度數據處理提供可靠的技術支撐.

1 時頻變換數據處理方法

1.1 小波變換與希爾伯特-黃變換

在進行激波風洞試驗時,測力系統受到來流的瞬間沖擊作用,產生突變信號,而且系統受到風洞流場的激勵作用,可能導致天平信號并不穩定.在有效試驗時間內,天平信號疊加有多個頻率隨時間變化的信號,是一個典型的非線性、非平穩的突變信號.風洞測力信號在不同的時間段有不同的頻率信號,而且每段頻率對應的振動幅值也不一樣,包括加載前的零值信號、加載后的氣動力動態信號以及一些其他不同頻率的非線性干擾信號,其時域波形圖如圖1 所示.

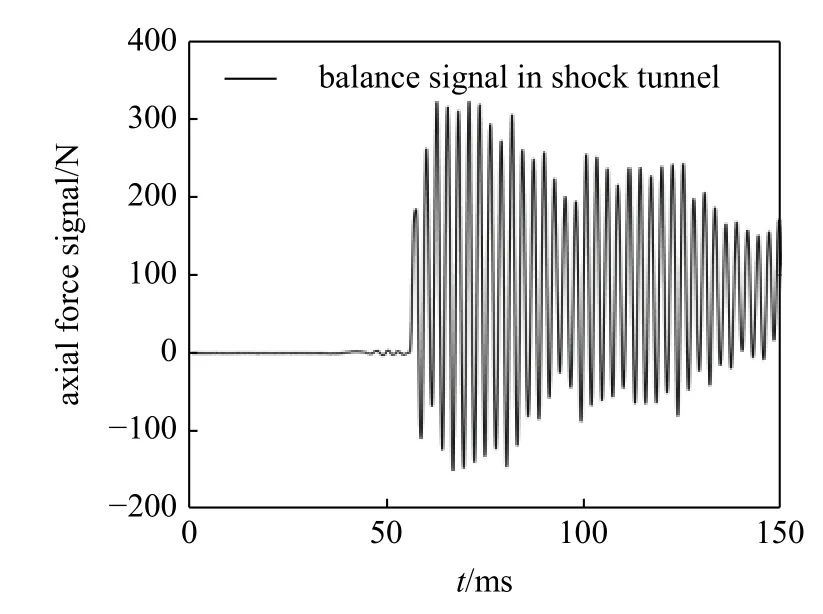
圖1 風洞測力信號(軸向力)Fig.1 Balance signal in shock tunnel (axial force)

作為時頻變換分析中最基本的方法之一,傳統的FT 分析采用無限長的三角函數基對整體信號進行線性變換,可以分析出信號中存在的頻率和幅值信息,但是不能表示隨時間變化的頻率信號,不宜分析非線性、非平穩的信號,其變換公式為

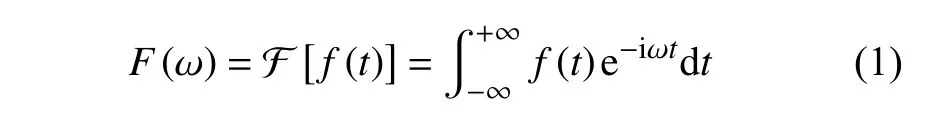
式中,變量 ω是頻率,F(ω) 是f(t) 的象函數,f(t) 是F(ω)的象原函數.在采用FT 處理突變信號時,會存在吉布斯效應,即采用三角函數擬合突變信號時會在信號跳變前后處產生數值振蕩現象.

WT 在FT 的基礎上將無限長的三角函數基替換成有限長的小波基,一維連續小波變換的公式為

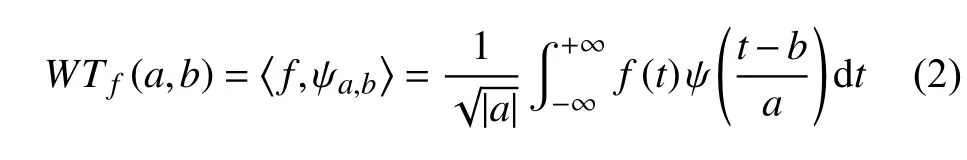
式中,變量a和b分別代表伸縮因子和平移因子,其中尺度a的值越大相當于FT 中頻率 ω 越小,平移量b對應FT 中的時間t.WT 通過小波函數基的伸縮和平移實現信號的時頻分析局部化,具有多分辨率性,很適合分析非平穩信號和提取信號的局部特征,常用于信號降噪和信號分解[22].相比于FT,WT 能夠同時在時域和頻域突出信號的局部特性,通過選取合適的小波函數能夠檢測信號的突變點,在突變信號的識別中具有廣泛的應用[23-24].

與傳統的信號處理方法相比,HHT 是針對處理非平穩信號而提出的,它徹底擺脫了線性和平穩性的束縛,能夠分析非線性、非平穩信號,同時,HHT不受Heisenberg 測不準原理制約,能夠在時間和頻率同時達到很高的精度,非常適用于分析突變信號[25].由于HHT 得到的瞬時頻率是局部性的,所以非常適合用于分析非線性、非平穩的信號,常用于故障診斷、地震數據處理等領域[26-28].本文針對脈沖型風洞測力天平信號的受沖擊振動特點,采用WT 和HHT 方法對激波風洞天平信號進行時頻變換分析處理.

1.2 天平信號的時頻變換分析方法

在將WT 和HHT 方法應用于風洞測力信號之前,需要先驗證該方法的可靠性.首先在激波風洞外搭建模型-天平-支撐測力系統,用天平階躍信號模擬風洞試驗時系統受到的沖擊激勵作用,構造理想的階躍載荷來簡化模擬系統受到的真實氣動力作用.針對天平階躍信號的時頻處理結果,并與理想階躍載荷對比分析,再將該方法應用于風洞測力信號中,從而獲得排除主要噪聲與振動干擾的、逼近實際加載的氣動力信號.

1.2.1 天平階躍信號的采集

采用SVDC 技術在激波風洞外采集天平階躍信號.SVDC 技術通過懸掛鋼絲對系統施加穩定的載荷,瞬間剪斷鋼絲對系統施加沖擊階躍載荷作用.與傳統敲擊模型表面的脈沖響應法[29-30]和懸掛砝碼的階躍響應法[31-34]不同的是,在鋼絲的彈性極限和懸掛鋼絲十字架的范圍內,SVDC 可以在任意方向施加任意大小的載荷作用,該載荷可以沿著天平體軸系自動分解成可以實時輸出的多分量載荷,更加適用于天平的動態校準處理,更加符合實際風洞試驗中的氣動力加載方式.

基于SVDC 技術在風洞外搭建天平階躍信號采集裝置,如圖2 所示.采集裝置與激波風洞試驗時的測力系統相同,由半錐角為10°、長度為750 mm 的尖錐標準模型、三分量脈沖型應變天平和彎刀支撐結構構成.采用該裝置對測力系統采集適量的階躍載荷信號,該信號在一定程度上反映了實際風洞試驗中的風洞測力信號的特征.

圖2 階躍信號采集裝置[21]Fig.2 Acquisition device of step load signal of balance[21]

選取采集到的任意一個天平階躍信號,將其時域波形圖繪制成圖3.該信號圖中虛線用于模擬受到流場起動瞬時沖擊激勵作用時測力系統的響應信號,實線表示的是構造的理想階躍信號,用于模擬簡化后的定常氣動力信號.天平階躍信號用于模擬簡化后的風洞測力信號,采樣頻率為50 kHz,信號時間是150 ms,包括前50 ms 的零值信號和加載后的100 ms 的氣動力信號,信號在第50 ms 時發生跳變,邊沿觸發時間忽略不計,理想階躍信號由0 N 突變為2.5 N 左右,并在后100 ms 內保持穩定不變.

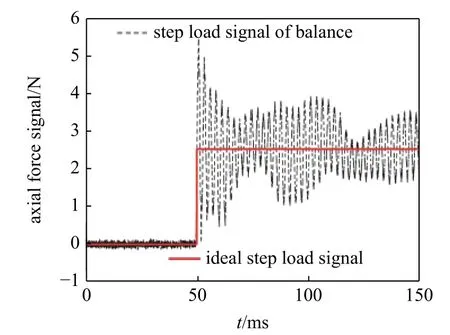
圖3 天平階躍信號與理想階躍信號(軸向力)Fig.3 Balance step signal and the ideal step signal (axial force)

1.2.2 天平階躍信號的降噪

在實際采集信號的過程中,采集信號不可避免地受到環境噪聲和其他噪聲的干擾,導致由辨識采樣信號得到的系統模型產生偏差,從而阻礙了系統控制精度的提高.采集的信號中重要信息的幅值比較大,但是數目比較少,而噪聲信息數目比較多,但其幅值較小.信噪比(signal-noise ratio,SNR)是信號與噪聲的比值,通常用來衡量降噪效果,信噪比越大,則信號中的噪聲成分越少,信號的質量越高[35].基于小波閾值處理思想的小波降噪技術原理簡單、計算量小,在保證良好的降噪效果的同時還可以盡可能保留原始信號的奇異性.小閾值降噪方法能獲得較好的降噪效果,并有效提高信號的信噪比,在信號處理中得到了廣泛地應用[36-39].

采用小波閾值降噪方法對天平階躍信號進行降噪處理,如圖4 所示.圖4 中虛線和實線展示的分別是經過小波閾值降噪前后的天平階躍信號,發現降噪前的信號含有許多噪聲干擾,尤其是在跳變前的零值信號段,其振動頻率比較高.經過計算得到小波降噪前后信號的信噪比分別為10.41 和10.84,降噪后的天平信號振動幅值并未產生很大的變化,但是去除了明顯的毛刺信號,整個信號變得更加平滑,有利于進行下一步時頻分析.

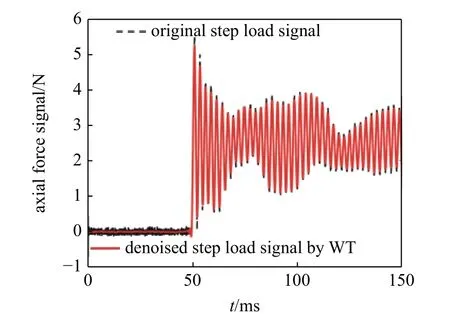
圖4 小波降噪前后天平階躍信號對比Fig.4 Original and the denoised step signal of balance by WT

2時頻變換在天平階躍信號中的應用

2.1 小波變換的應用

WT 具有良好的時頻局部化特性,通過伸縮和平移小波函數對信號進行多分辨率分析(multiresolution analysis,MRA),能夠解決傅里葉變換不能解決的諸多困難問題[39].小波分解是應用小波降噪方法對原始信號進行近似分解和細節分解,分解得到小波近似系數(低頻系數)和小波細節系數(高頻系數);小波重構是將小波分解的逆過程,可以選取小波分解后的適當系數進行信號重構.在實際應用中,信號中的低頻分量往往比較重要,能夠近似的展示整個信號的大致趨勢,而高頻分量可以展示整個信號的細節成分,對信號起到修飾作用.小波分解一般可以表示為由一對互補的低通濾波器和高通濾波器組成,原始信號經過一級小波分解后得到低頻系數和高頻系數,此時,可以繼續對低頻系數進行不斷的分解,而分解的技術取決于要分析的信號數據和用戶的具體需要[40].

采用小波函數10 階緊支集正交小波(即小波函數dB10)對降噪后的天平階躍信號進行8 級小波分解,將得到的低頻系數A1～A8 與高頻系數D1～D8 進行對比,如圖5 所示.根據小波分解的原理,在時域內有

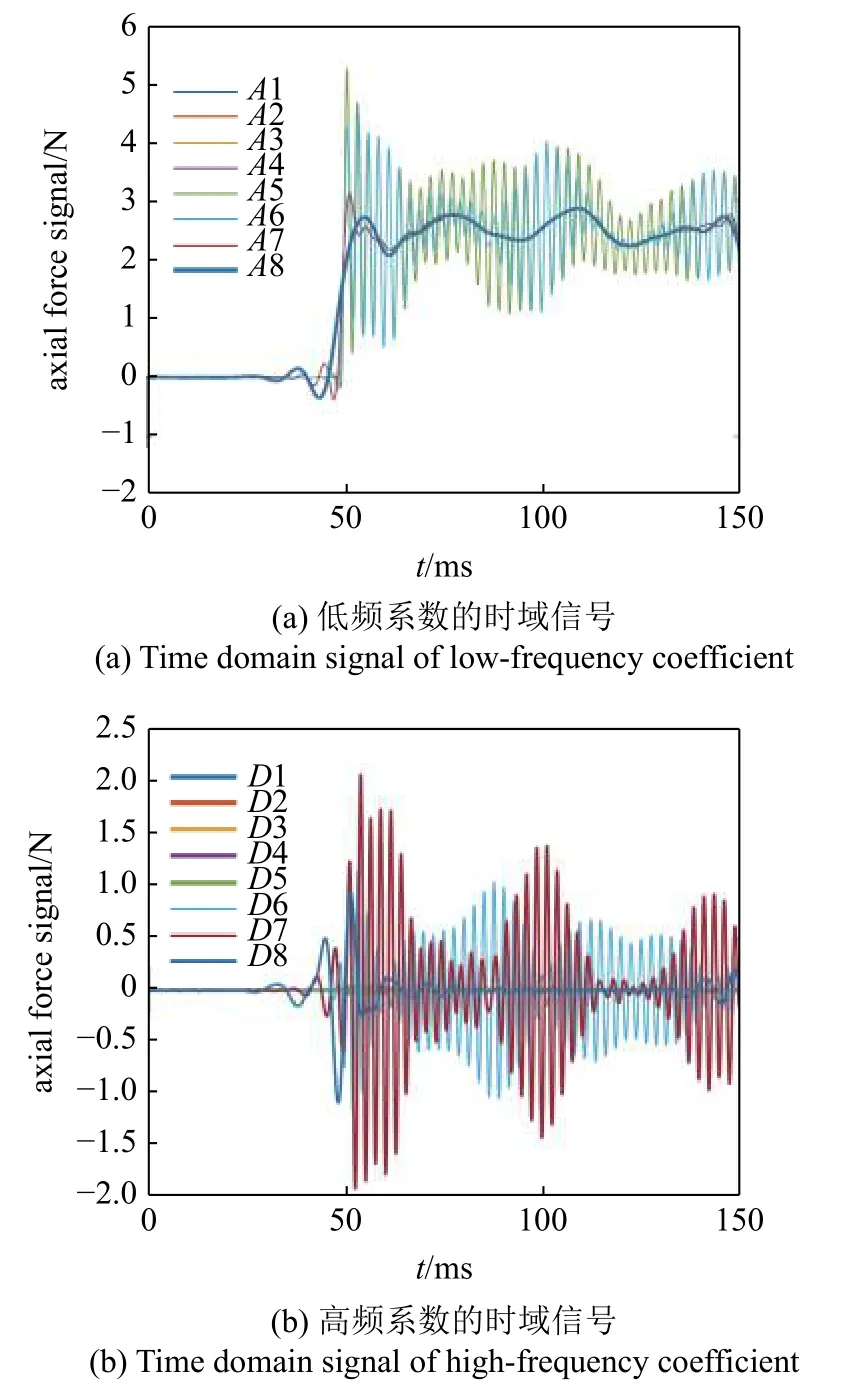
圖5 天平階躍信號分解出的低頻系數與高頻系數Fig.5 Low-and high-frequency coefficient of the balance step signal by WT

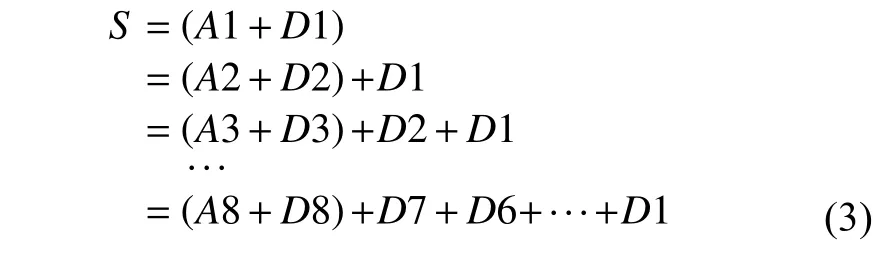
式中,S為經過小波降噪去毛刺后的天平階躍信號,A1～A8 和D1～D8 分別為經過8 級小波分解得到的低頻系數和高頻系數.

在圖5 中,低頻系數A1～A5 與原始信號基本保持了相同的波形,展示了原始信號的近似信息,而高頻系數反映了原始信號的細節信息.對低頻系數A1～A8、高頻系數D1～D8 和理想階躍信號作快速傅里葉變換(fast fourier transform,FFT)分析,并計算信號的99%占用帶寬,即該帶寬頻率范圍內的信號功率占總信號功率的99%,將部分結果整理至表1 所示.根據圖5 和表1 可知,理想階躍信號的99%占用帶寬為0.00～ 200.00 Hz.高頻系數D1～D5 幅值較小,基本趨近于零且保持穩定,其頻率非常高,均在240.00 Hz 以上,相對于原始信號可以當作高頻噪聲干擾濾掉.D6 和D7 占據高頻系數主導地位,其幅值與原始信號相當,其主要頻率為380.00 Hz,將兩者進行小波重構可以反映系統慣性振動頻率.D8 的99%占用帶寬是73.33～ 240.00 Hz,與理想階躍信號有重疊部分,所以D8 不能完全當作干擾信號濾掉.

根據表1 中的數據,濾掉高頻系數D1～D7 后的低頻系數A7 初步反映出理想階躍載荷的特征,其頻率符合理想階躍信號的99% 占用帶寬,將其與理想階躍信號進行對比,如圖6 所示.圖6(a)和圖6(b) 分別表示的在時域波形圖和頻域幅度頻譜圖的對比,虛線是經過小波降噪去毛刺后的天平階躍信號,點劃線是理想階躍信號,實線表示經過8 級小波分解后的第7 級低頻系數A7.相比于天平階躍信號S,A7 已去掉了大部分振動干擾信號,其中S的主要頻率為380.00 Hz 左右,驗證了測力系統的慣性振動頻率為380.00 Hz.

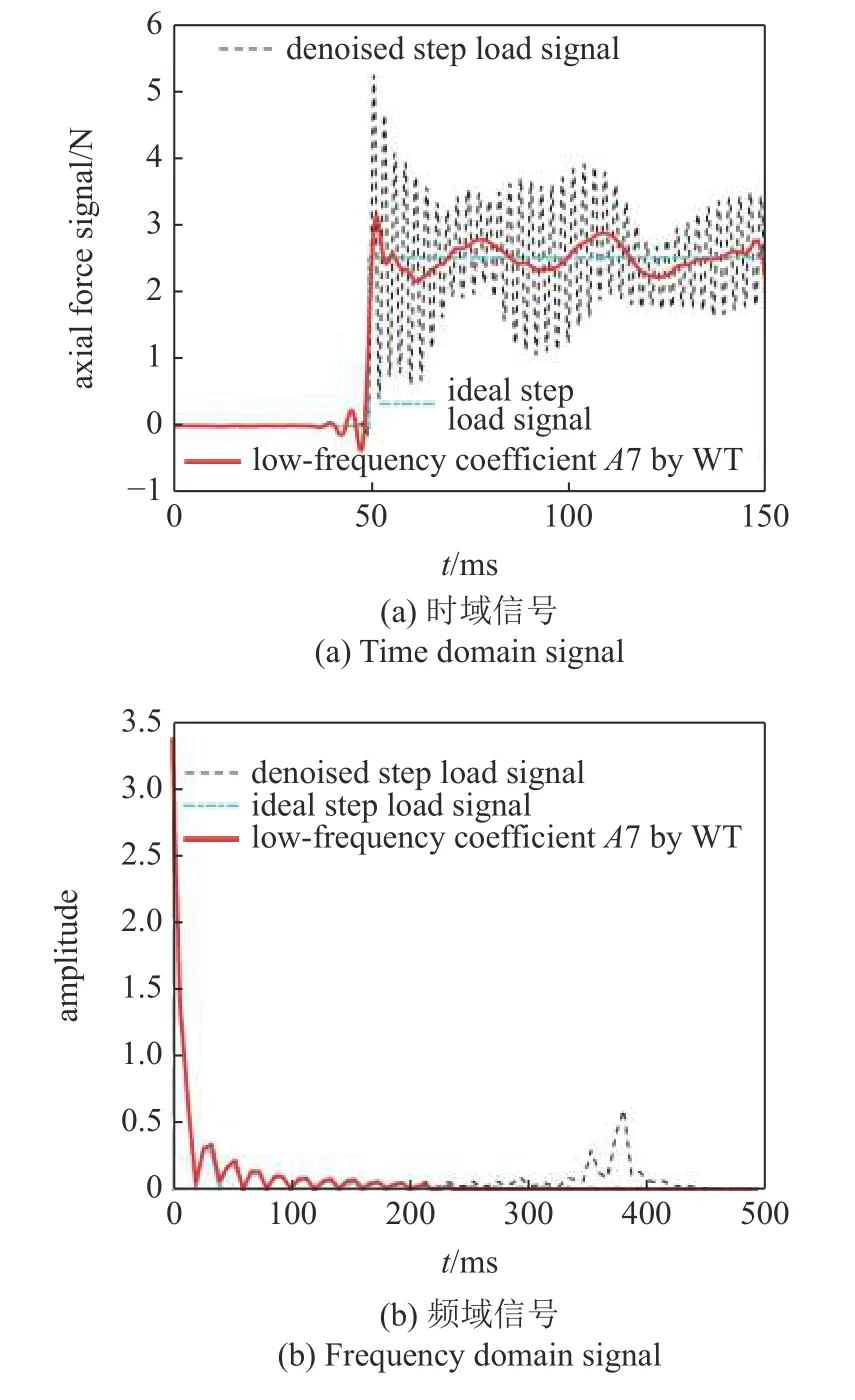
圖6 天平階躍信號與WT 處理得到的低頻系數A7Fig.6 Balance step signal and low-frequency coefficient A7 by WT processing

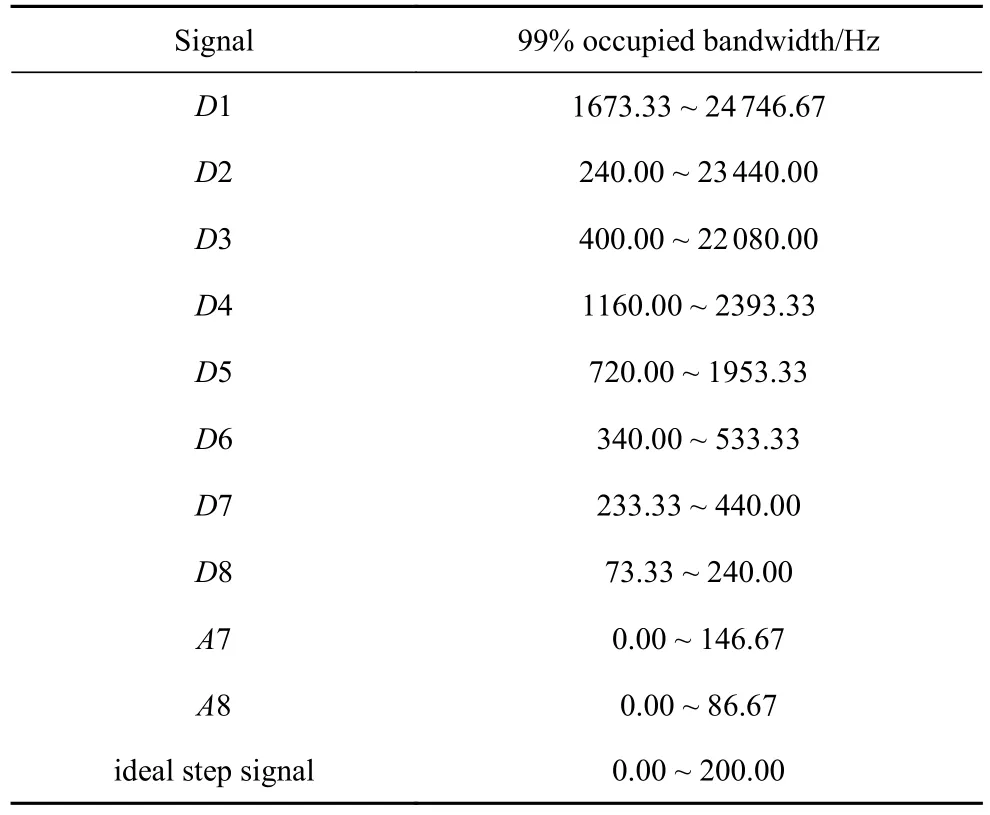
表1 8 級小波分解后的信號的99%占用帶寬Table 1 99% occupied bandwidth of the signal after 8-level wavelet decomposition

2.2 希爾伯特-黃變換的應用

采用HHT 方法處理信號的具體過程包含兩步,第一步是由Huang 提出的利用經驗模態分解(empirical mode decomposition,EMD)方法將待處理的信號分解為一系列滿足一定要求的固有模態函數(intrinsic mode function,IMF)與一個剩余分量(residual);第二步是由Hilbert 提出的針對每一個IMF 進行希爾伯特譜分析(Hilbert spectrum analysis,HSA),從而得到相應的瞬時頻率、瞬時幅值和Hilbert 譜[41].由于HHT 方法容易受到高頻噪聲的影響,所以首先對天平階躍信號進行高頻降噪處理,經過小波分解降噪后的低頻系數A5 濾掉了533.33 Hz 以上的頻率,可以采用HHT 進行處理分析.

因此,利用HHT 中Huang 提出的EMD 方法對低頻系數A5 進行3 級處理,得到3 個固有模態函數IMFs 和一個剩余分量residual,如圖7 所示.在時域內有

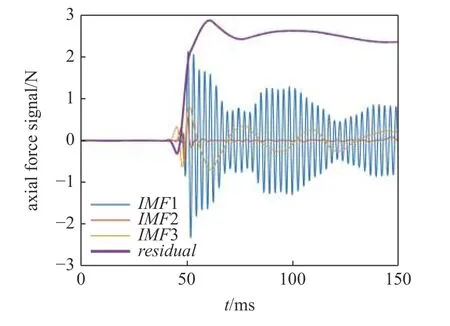
圖7 天平階躍信號與EMD 得到的IMFs 和residualFig.7IMFs and residualof the balance step signal by EMD processing

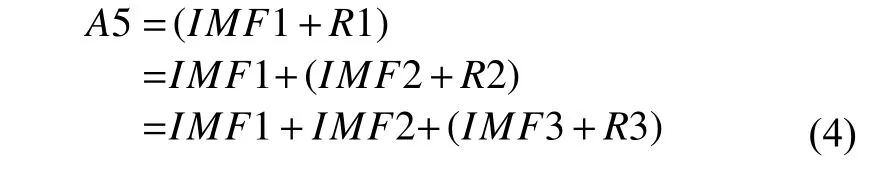
式中,A5 是天平階躍信號經過小波分解濾掉高頻系數D1～D5 后的低頻系數A5,基本無高頻噪聲的干擾,IMF1～IMF3 分別是天平階躍信號經過3 級EMD 處理后的固有模態函數,R1～R3 是天平階躍信號經過3 級EMD 處理后的剩余分量.

利用HHT 中Hilbert 提出的HSA 方法對得到的IMFs 進行Hilbert 譜分析,得到每一個IMF的瞬時頻率,整理至如圖8 所示.

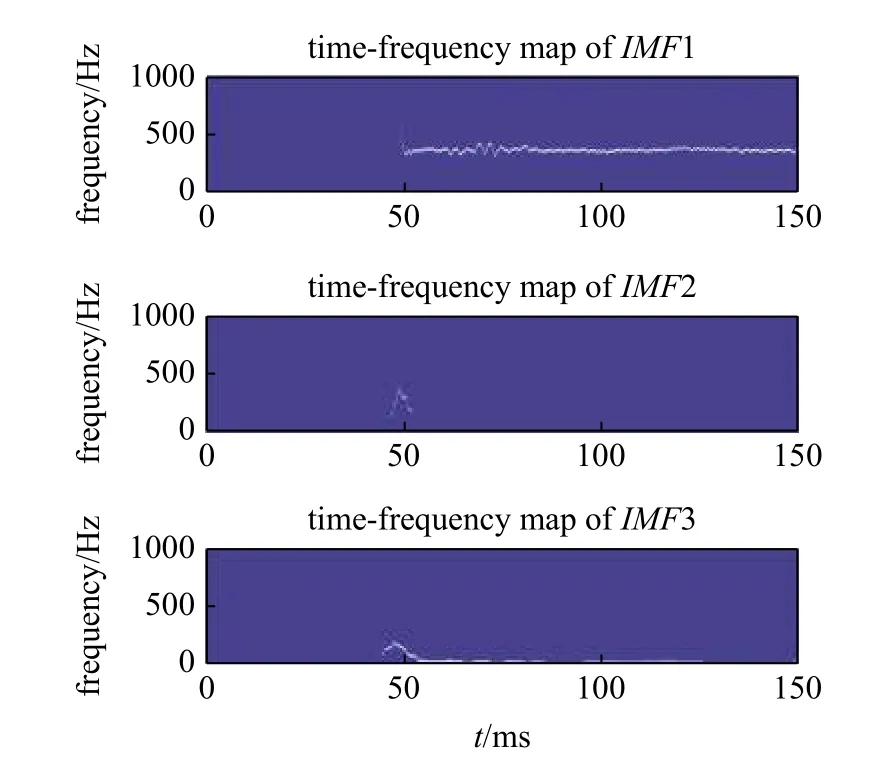
圖8 天平階躍信號經過HSA 得到IMFs 的時頻圖Fig.8 Time-frequency map of IMFs of the balance step signal by HSA processing

計算IMFs 和R3 的99%占用帶寬,整理結果至表2 所示.圖7 中第一級IMF1 與原始信號波形相似,基本反映了原始信號的近似值,占據原始信號中的主導地位,其主要頻率為380.00 Hz,與小波分解得到的慣性振動頻率相同.IMF2 和IMF3 反映了信號的細節值,其占有比例較小.IMF2 僅在信號跳變時有幅值,而在信號跳變后其幅值保持穩定且趨于零.IMF3 在信號跳變后的時間段內一直存在波動,根據圖8 中IMF3 的瞬時頻率發現其主要頻率為33.33 Hz 左右,完全位于理想階躍信號的99%占用帶寬內,所以不能將IMF3 當作低頻干擾信號直接濾掉.

根據表2 中的數據,濾掉固有模態函數IMF1和IMF2 后的剩余分量R2 完全符合理想階躍信號的99%占用帶寬,且基本反映出理想階躍信號的特征,將時域和頻域范圍內的對比結果整理如圖9 所示.

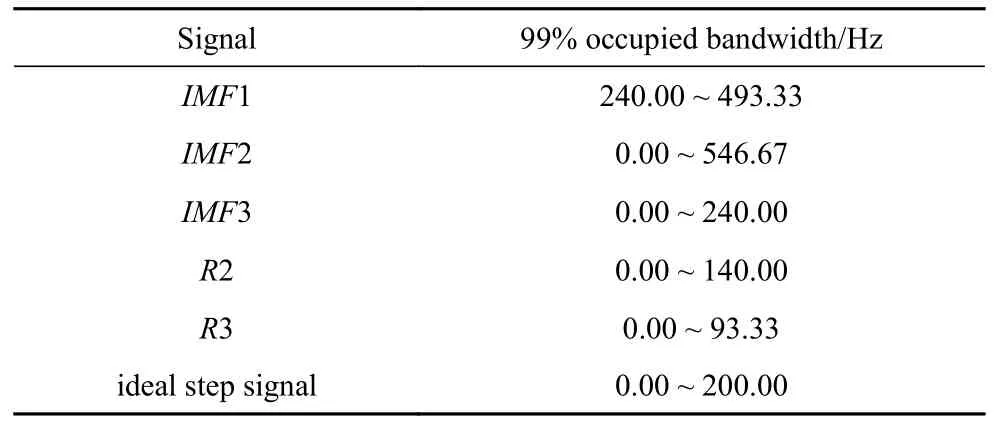
表2 HHT 處理后的信號的99%占用帶寬Table 2 99% occupied bandwidth of the signal by HHT processing

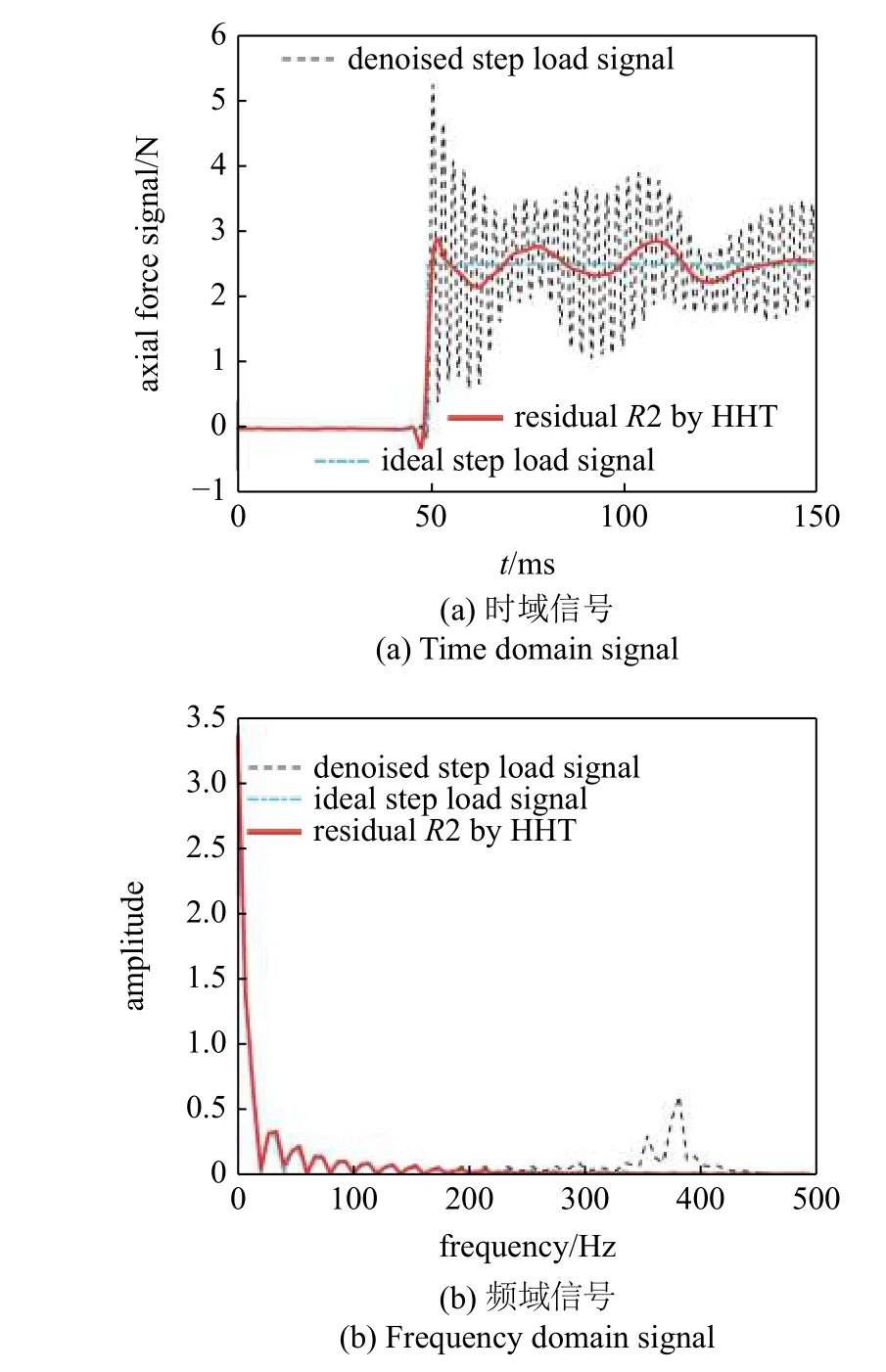
圖9 天平階躍信號與HHT 處理得到的剩余分量R2Fig.9 Balance step signal and residual R2 by HHT processing

2.3 天平信號處理結果驗證與誤差分析

對天平階躍信號進行降噪處理時,經過小波分解后的高頻系數D1～D5 是信號中的高頻低幅值噪聲干擾成分,去掉該噪聲干擾后的低頻系數A5 與原始信號基本保持了相同的波形和幅值,但是去掉了明顯的毛刺信號.將經過WT 和HHT 方法應用于天平階躍信號后的A7 和R2 進行對比分析,如圖10所示.高頻系數D6 和D7 之和以及固有模態函數IMF1 具有相同的波形,其主要頻率是380.00 Hz,反映了測力系統振動的慣性頻率.高頻系數D8 和固有模態函數IMF2 在50 ms 附近產生信號跳變,作用時間短,作用力大,而在信號跳變后,幅值變為零,反映了在采集信號時剪斷鋼絲瞬間對系統產生的沖擊載荷作用.圖10 中天平階躍信號經過WT 處理后的A7 存在吉布斯效應,在信號跳變前后處存在數值振蕩,而經過HHT 處理后的R2 有效地抑制了吉布斯效應,說明HHT 更適合處理突變信號.

為了驗證WT 和HHT 方法應用于天平階躍信號的可靠性,采用相對誤差 δ 對處理結果進行對比驗證,相對誤差反映了處理方法的可信程度.選取跳變后的數據進行分析,對圖10 中經過WT 和HHT 處理后得到的A7 和R2 進行分析,截取時間區間70～100 ms 內的數據平均化處理得到近似值,對理想階躍信號進行平均化處理得到真實值,根據相對誤差的定義式(3)計算得到WT 和HHT 處理結果的相對誤差 δW和δH

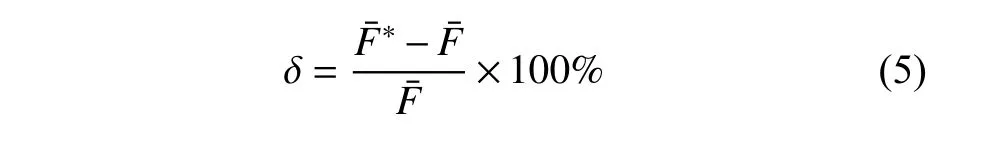
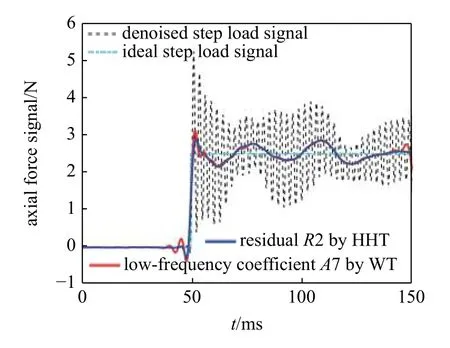
圖10 天平階躍信號經過WT 和HHT 后的結果Fig.10 Comparison of the balance step signal by WT and HHT processing

表3 中的數據展示了經過WT 和HHT 處理后的結果與理想階躍信號之間的相對誤差,兩種處理方法的相對誤差值均比較小,分別為1.04% 和1.20%,與參考文獻[21]中采用智能模型處理得到結果的相對誤差(1%)相當,精準度均比較高,驗證了WT 和HHT 方法的可靠性.由表3 中WT 和HHT方法結果對比發現,兩種方法處理天平階躍信號的可靠性均比較高,且處理結果比較接近.

表3 WT 和HHT 處理結果的相對誤差Table 3 Relative error of the balance step signal by WT and HHT processing

3時頻變換在風洞測力信號中的應用

經過對WT 和HHT 方法應用于天平階躍信號的驗證分析,發現這兩種時頻變換處理方法對信號中的慣性振動干擾和其他高頻干擾信號辨識的非常理想,因此嘗試將該方法應用于風洞測力信號的數據處理.2012 年,中國科學院力學研究所成功研制復現高超聲速飛行條件激波風洞(簡稱“JF-12 復現風洞”),該風洞可復現25～ 40 km 高空、馬赫數5～9 飛行條件的高超聲速飛行器氣動試驗,有效試驗時間超過了100 ms.自JF-12 復現風洞建成以來,開展了大量的高超聲速飛行器氣動力測量試驗,并獲得了大量高精度的可靠測力數據[42].嘗試采用WT 和HHT 方法應用于在JF-12 復現風洞中進行的750 mm 尖錐標準模型測力試驗中的天平信號的數據處理,獲得高精準度的動態氣動力信號.

3.1 小波變換應用于風洞測力信號

相對于在激波風洞外采集的天平階躍信號,通過激波風洞試驗獲得的風洞測力信號受到風洞流場的影響,可能會產生額外的干擾信號,所以在8 級小波分解的基礎上,采用小波函數dB10 對低頻系數A8 進行進一步小波分解,即對風洞測力信號進行9 級小波分解,將得到的相應的低頻系數A1～A9 和高頻系數D1～D9 整理如圖11 所示.

對圖11 中的低頻系數A1～A9 和高頻系數D1～D9 作FFT 分析并計算信號的99%占用帶寬,將部分結果展示在表4 中.將風洞測力信號與天平階躍信號經過小波分解后的低頻系數與高頻系數一一比對,發現高頻系數D1～D5 相對于原信號均為高頻信號,且幅值基本趨于零,辨識為高頻噪聲信號.風洞測力信號分解出的高頻系數D6 和D7 的主要頻率為366.67 Hz,與系統的慣性頻率相對應,驗證了高頻系數D6 和D7 是系統慣性振動產生的干擾信號.雖然風洞測力信號和天平階躍信號分解出的D8 和D9 具有相似的99%占用帶寬,且均與理想階躍信號的帶寬存在重疊部分,但是風洞測力信號的高頻系數D8 和D9 在50 ms 后的整個時間段中一直存在波動信號,因此初步認為D8 和D9 是風洞流場引起的低頻干擾信號.

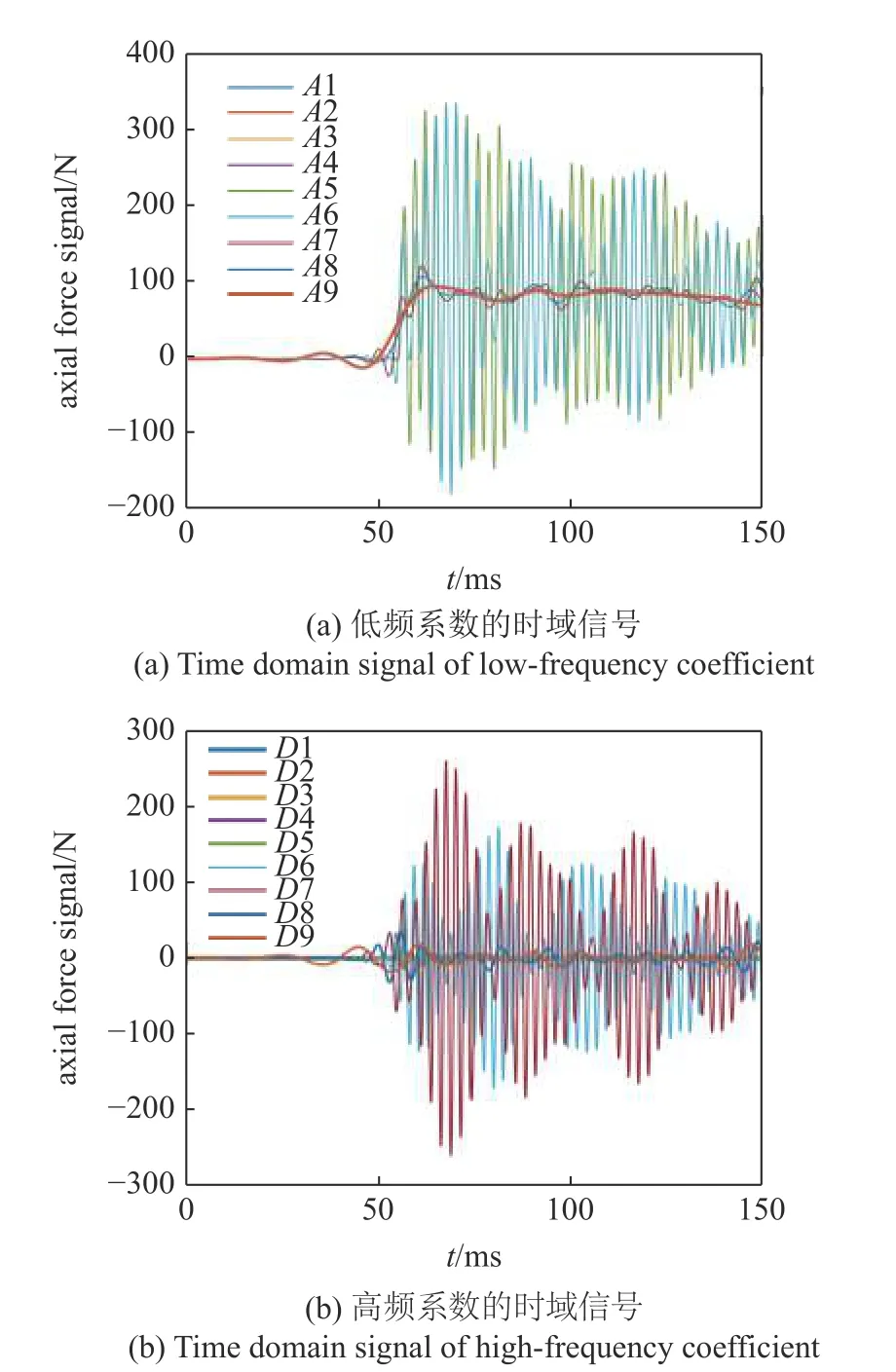
圖11 風洞測力信號分解出的低頻系數與高頻系數Fig.11 Low-and high-frequency coefficient of the balance signal in shock tunnel by WT

根據表4 中A9 的數據發現,A9 完全符合理想階躍信號的99%占用帶寬.圖12 展示的是風洞測力信號與經過小波分解后得到的氣動力信號A9 的對比圖.從時域信號對比圖可以看出,經過WT 處理后的A9 基本達到了理想階躍信號的要求,在信號跳變后基本保持穩定.從頻域信號對比圖可以看出,A9 相對于風洞測力信號不僅濾掉了主要頻率為366.67 Hz 的系統慣性振動信號,而且成功濾掉了其他高頻振動信號以及部分低頻干擾信號,基本達到了理想階躍信號的頻率要求,反映出真實氣動力信號的主要特征.

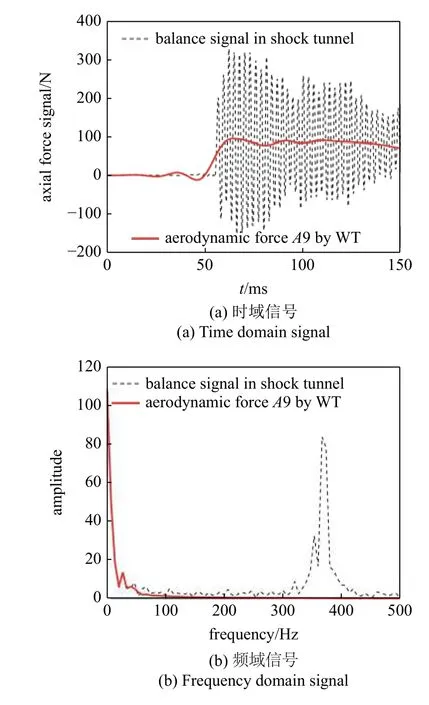
圖12 風洞測力信號與WT 處理得到的氣動力信號Fig.12 Balance signal in shock tunnel and the aerodynamic force signal by WT processing

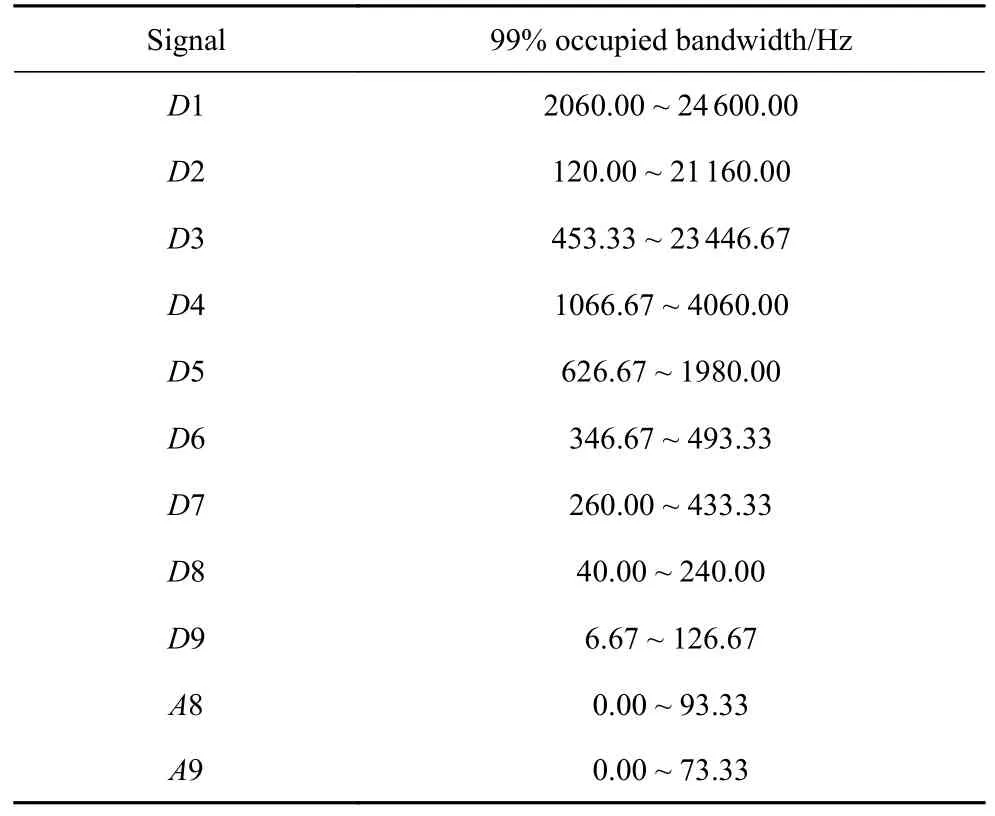
表4 小波9 級分解后的信號的99%占用帶寬Table 4 99% occupied bandwidth of the signal after 9-level wavelet decomposition

3.2 希爾伯特-黃變換應用于風洞測力信號

采用HHT 中的EMD 對風洞測力信號分解出的低頻系數A5 進行3 級分解,得到3 個固有模態函數IMFs 和一個剩余分量residual,其時域信號圖如圖13 所示.

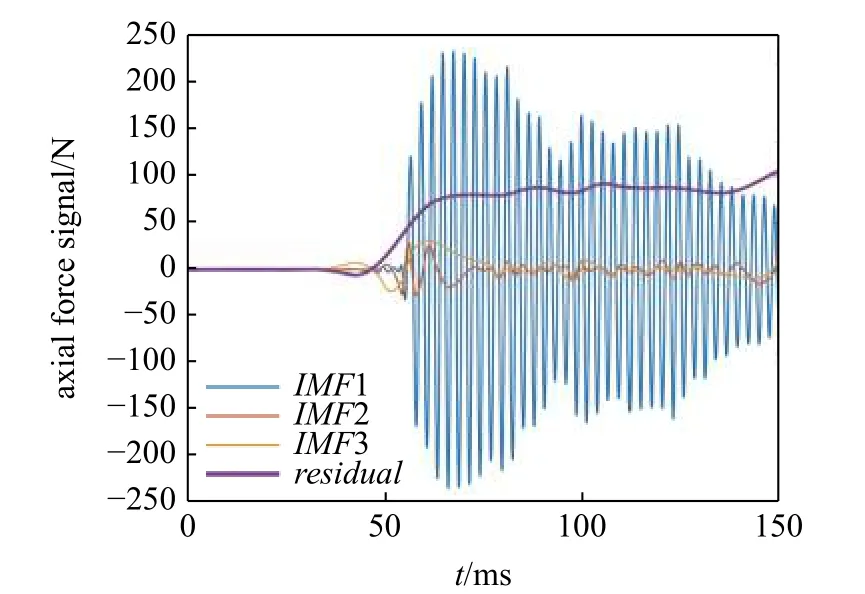
圖13 風洞測力信號與EMD 后的IMFs 和residualFig.13IMFs and residualof the balance signal in shock tunnel by EMD processing

然后對每一個IMF進行HSA 處理,得到相應的瞬時頻率,其時頻圖如圖14 所示.計算每一個IMF和residual的99%占用帶寬,將部分結果整理至表5 所示.將風洞測力信號經過HHT 處理的結果與天平階躍信號的結果進行對比,第一級固有模態函數IMF1 均占據原始信號的主導地位,其中風洞測力信號的IMF1 主要頻率為366.67 Hz,與WT 處理后的慣性振動頻率相同.與天平階躍信號不同的是,風洞測力信號IMF2 和IMF3 在50 ms 后的整個時間段內均存在波動信號,且頻率較低,幅值較小,初步認為是風洞流場產生的低頻干擾信號.

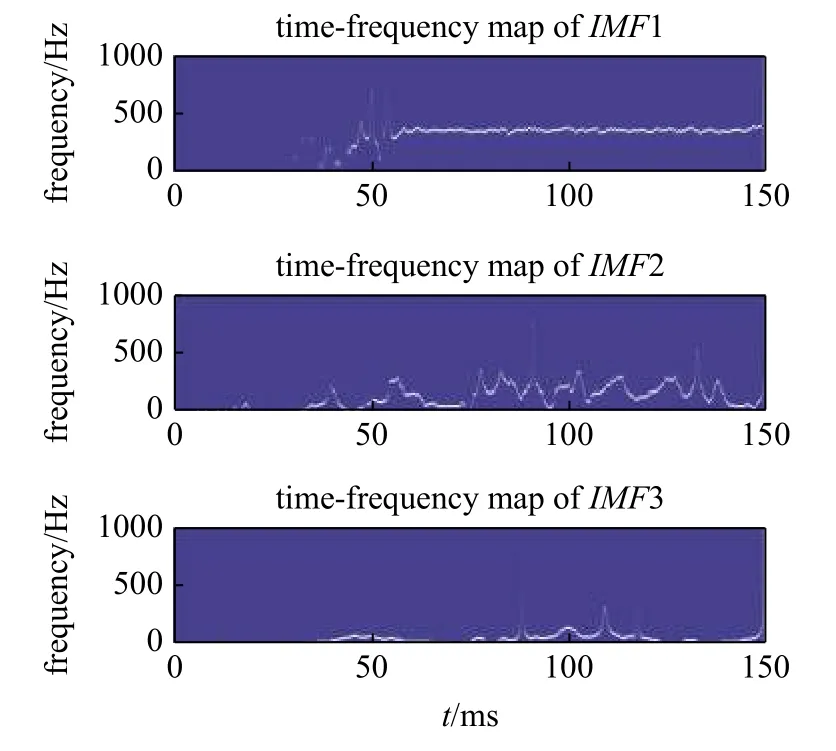
圖14 風洞測力信號經過HSA 得到IMFs 的時頻圖Fig.14 Time-frequency map of IMFs of the balance signal in shock tunnel by HSA processing

表5 HHT 處理后的信號的99%占用帶寬Table 5 99% occupied bandwidth of the balance signal in shock tunnel by HHT processing

表5 中R3 的數據顯示了經過HHT 處理后得到的剩余分量R3 的99%占用帶寬位于理想階躍信號的頻率帶寬內.將風洞測力信號與R3 進行時域和頻域的對比,結果如圖15 所示.從時域信號對比圖中看出,經過處理后的得到的剩余分量R3 基本達到了理想階躍信號的要求,在信號跳變后一直保持穩定,從頻域對比圖發現R3 不僅完全濾掉了主要頻率為366.67 Hz 的系統慣性振動信號,而且濾掉了高頻噪聲干擾與部分低頻干擾信號.

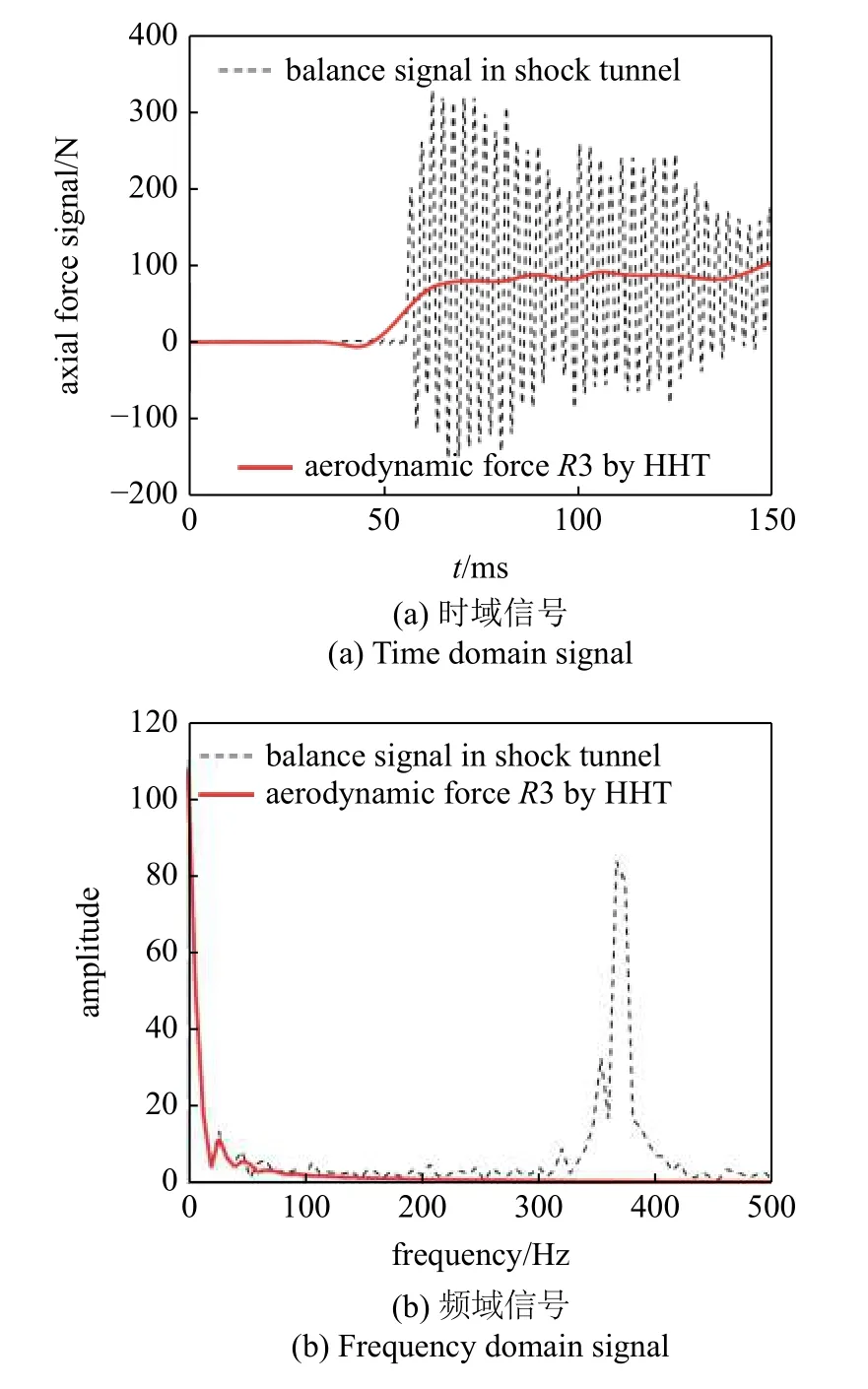
圖15 風洞測力信號與HHT 處理得到的氣動力信號Fig.15 Balance signal in shock tunnel and the aerodynamic force signal by HHT processing

3.3 測力信號處理結果對比分析

將經過WT 和HHT 方法處理后的風洞測力信號的結果進行對比分析.高頻系數D6 與D7 之和和固有模態函數IMF1 具有相同的振動頻率和幅值,波形基本重合,主要頻率為366.67 Hz,與天平階躍信號得到的測力系統的慣性振動頻率380.00 Hz 基本保持一致.與天平階躍信號不同的是,風洞測力信號小波分解得到的D8 和D9 與HHT 得到的IMF2和IMF3 相對應,在50 ms 后的整個時間段內存在波動,反映了在風洞流場建立后,測力系統一直受到非定常載荷作用,從而產生了低頻信號,該信號在天平階躍信號中并未出現,因此,D8,D9 和IMF2,IMF3為風洞流場產生的低頻干擾信號.如圖16 所示,風洞測力信號經過WT 和HHT 處理后的A9 和R3 均基本反映出真實氣動力的信號的特征.但是,WT 處理后的A9 在信號跳變前后仍存在數值振蕩,而HHT 處理后的R3 在信號跳變處表現比較平滑,在處理突變信號時,HHT 處理效果更佳.

對風洞測力結果進行相對偏差分析,將經過WT 和HHT 處理后得到的A9 和R3 與參考文獻[21]中FMS 的氣動力結果進行對比,以FMS 的氣動力結果為參考值,計算圖16 中的A9 和R3 的相對偏差(RD),截取時間為70～ 100 ms 內的數據進行平均化處理得到近似值aˉ,根據軸向力大小計算其軸向力系數,與FMS 的結果對比得到WT 和HHT 處理結果的相對偏差RDW和RDH,將計算結果整理至表6中.其中相對偏差的計算公式為

圖16 風洞測力信號經過WT 和HHT 后的結果Fig.16 Comparison of the balance signal in shock tunnel by WT and HHT processing

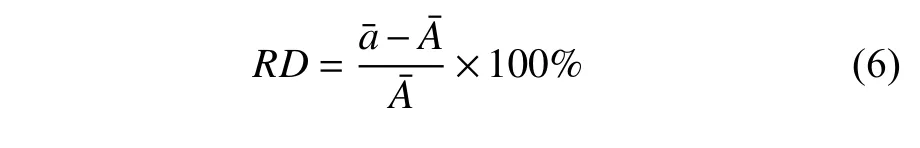
表6 中的數據顯示經過WT 和HHT 處理得到的結果與FMS 的氣動力結果的相對偏差非常小,表明基于WT 和HHT 的時頻變換處理方法在激波風洞天平信號應用中具有較高的可靠性.同時,WT 方法常用于處理信號與噪聲頻率相差較大的信號,針對頻率比較相近的信號,HHT 方法更加適用.而HHT 方法在降噪方法的效果可能不如WT 方法,可以首先采用WT 對信號進行降噪處理,然后再采用HHT 對信號進行時頻變換分析處理[43].經驗證,這兩種時頻變換方法在脈沖風洞瞬態測力試驗中均具有較高的應用價值.

表6 WT 和HHT 處理結果的相對偏差Table 6 Relative deviation of the balance signal in shock tunnel by WT and HHT

4 結論

本文采用WT 和HHT 方法對尖錐標準測力模型在激波風洞測力試驗中的天平輸出信號開展了時頻變換分析與處理,數據處理結果表明該方法不僅能精準辨識出測力系統的慣性振動信號,而且能有效地辨識出風洞測力信號中的其他高頻和低頻干擾信號.經過處理成功去掉了天平信號中的主要干擾信號,獲得了濾除干擾后的動態氣動力載荷信號.本研究對天平沖擊階躍載荷信號的數據處理結果驗證了時頻變換方法的有效性和可靠性.

目前,基于人工智能技術的測力天平智能化研究比較新穎,相關方法和技術仍處于發展階段,本研究中的數據信號時頻處理方法可直接用于天平智能化研究的樣本數據預處理.這兩種時頻處理方法在激波風洞測力試驗中具有應用前景,將為我國高超聲速飛行器高焓氣動特性精確評估提供關鍵技術和數據支撐.