高階相關峭度反卷積逆濾波器及磁導航野點識別?

黃卓群 楊光永 程 滿 劉 葉

（云南民族大學電氣信息工程學院 昆明 650500）

1 引言

AGV是輪式移動機器人的一種典型代表，它通常采用磁條導航來預設行駛路線，將磁條粘貼在地面上，AGV 循跡磁條來進行移動。在AGV 行駛過程中，由于實際環境較為復雜，例如磁條兩側會有磁條碎片或雜散磁場而導致的磁條磁場發生變化使得傳感器獲取到包含異常點的信號，從而降低了機器人的行駛平穩性，嚴重時甚至會引起AGV脫軌。異常點指小部分樣本嚴重偏離動態目標變化趨勢的偽數據，或遠離動態目標隨機過程的離群值［1］，它是一項主要涵蓋傳感器技術、信號處理技術、模式識別技術、統計學和算法分析等多種技術與學科為一體的綜合性的研究方向，在目標跟蹤、圖像信號處理、精密測量、病理分析、故障識別、刑事偵查、野生動物保護，甚至宏觀經濟調控、特困扶貧、反恐防恐、交通指揮、德育教育等領域都有廣泛而深遠的研究價值和應用前景。異常點作為一種非平穩分布的隨機過程，其模式識別和消除是導航信號感知和信號處理的重要任務。1983 年，Dw?yer 第一次提出了譜峭度的含義，峭度是一個無量綱參數或者統計量。峭度對信號中的瞬態成分十分敏感，常被用于滾動軸承的狀態監測以及故障診斷中。由于磁導航信號在野點干擾下，趨于非平穩分布，故將峭度的含義引入磁導航信號處理辦法中。2012 年，McDonald 提出了最大相關峭度反卷積算法，在早期，該算法被用于故障信號的檢測。文獻［2］以輸出信號峭度的絕對值和接近性量度函數的乘積作為目標優化函數，有效避免了人為選擇閾值參數和步長。文獻［3］以峭度絕對值為對比函數推導出一種一單元ICA-R固定點算法，避免了對比函數二階導數的計算，簡化了運算復雜度。文獻［5］提出了一種改進的優化學習算法，在牛頓迭代方向上增加精確線性搜索，從而使得算法的收斂性不依賴于μ的人為選擇。文獻［7］提出一種改進的基于峭度的盲分離算法，可以自適應地確定激活函數。文獻［8］針對雙梯度的盲源分離算法進行了研究，以信號的峭度為代價函數對其進行了改進。文獻［9］通過建立步長因子與峭度的平方和之間的非線性關系，提出了一種自適應的自然梯度算法。文獻［10］提出了一種自適應學習率盲信源分離的自然梯度算法。文獻［11］提出了基于峰度的自適應盲信號分離切換算法，用于語音信號盲分離處理。基于峰度的BSS 切換算法在分離前后的信號波形和頻譜以及主要評估參數方面具有良好的信號分離效率，具有比JADE FOBI 算法更好的分離效率。文獻［12］作者使用最大三階相關峭度反卷積算法對激光位移信號和多重反射信號進行提取。文獻［13~14］提出了常見混合模型的盲源分離方法。文獻［15~16］主要闡述了改進的獨立分量分析算法。傳統的自適應濾波器、高階統計量濾波器或聚類等方法因缺乏先驗知識，難以建立準確的參考模型，出現病態、收斂速度快速降低等問題。因此，本文針對非平穩信號的統計特性，利用相關峭度來度量混合信號變化的統計特性，使用四階相關峭度反卷積（M4CKD）算法，針對于沒有任何參考模型的信號，對其進行盲提取。

2 磁導航信息檢測

本實驗采用的是八位磁導航傳感器，AGV 運行時，采用了磁導航循跡偏差算法，我們將偏差零點設置在導航傳感器的中部位置，當地面磁條位于傳感器中部時，此時的偏差為0。我們將8 位傳感器的中心位置的權值記為8.5，即在該位置AGV是無偏移行駛，AGV 行駛路徑圖如圖1所示。循跡偏差算法的表達式為

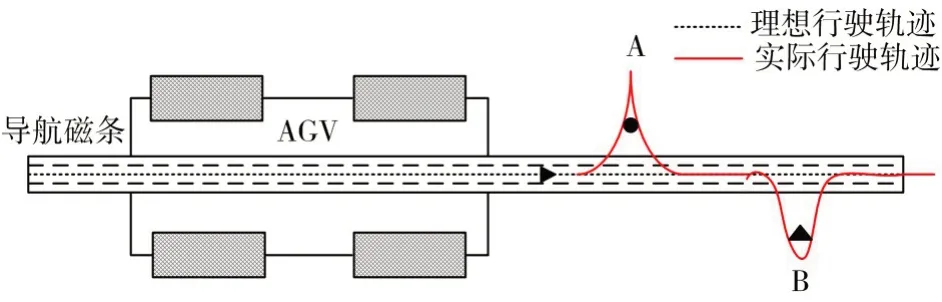
圖1 AGV行駛路徑圖

該式中，Si為每個位置磁導航傳感器的權值，M是觸發磁導航傳感器的個數，ε為偏移距離。

3 算法模型

3.1 最大相關峭度反卷積算法

在2012 年，McDonald 提出了最大相關峭度反卷積算法，該算法早前用于軸承故障檢測，對故障信號進行檢測。

離散信號為：y(n)=h(n)*x(n)+e(n)，x(n)是原始序列，e(n)是噪聲，y(n)是輸出信號，h(n)是系統函數。該算法主要是要尋找一個FIR 濾波器，使得x(n) 的相關峭度達到最大時，由y(n) 恢復出x(n)。它主要針對的是原始序列中脈沖跳動比較大的信號，對其進行處理，將相關峭度作為代價函數，當原始信號的相關峭度達到最大時，迭代終止。最大相關峭度反卷積算法中相關峭度的定義為

其中，T為信號的周期，M為位移數。M的數量越多，反卷積的脈沖序列也就越多，更有利于提高算法的檢測能力。

3.2 算法設計

峭度CK是反映隨機變量分布特性的數值統計量是歸一化的4 階累積量。 用公式表示峭度，其中xi為信號值，xˉ為信號均值，N為采樣長度，σt為標準差。

磁導航傳感器位于AGV 底部的正中心位置，接受到的n維原始信號為U(k)=[u1(k),u2(k),…,un(k)]T，n維觀測噪聲為N(k)=[n1(k),n2(k),…,nn(k)]T，該混合模型經過一個系統傳遞函，其中p為延遲時間，則非平穩信號的觀測序列X(k)為

設置Wp(k)為逆濾波器，該逆濾波器的傳遞函數為，可以得到觀測序列X(k)和逆濾波器Wp(k)的卷積輸出為

其中，y(k)=[y1(k),y2(k),…,yn(k)]T。

設輸出矢量y(k)的采樣周期為T，定義y(k)的四階相關峭度C(T)為

其中i=1,2,…,n。當四階相關峭度達到最大時，逆濾波器獲得最優迭代解Wopt(k) ，此時最優解Wopt(k)與H(z)*N(k)的卷積為0，經過濾波器輸出的異常點分量為0，磁導航原始信息被提取，表示為

對上式公式進行簡化運算，得到M4CKD 算法盲提取信號的輸出公式的一般形式為

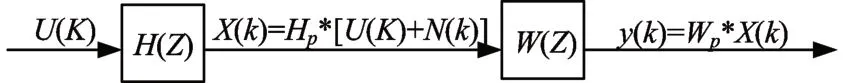
圖2 混合信號提取系統結構框圖

3.3 逆濾波器的解

對于求解逆濾波器Wp(k)，得到逆濾波器的最優解的必要條件就是使四階相關峭度對逆濾波器的偏導數為0，即：，帶入表達式可得：

因為X(k) 非平穩信號，所以有設：

可得到：

即：

由此可求得逆濾波器的最優迭代解為

其 中 ：

4 算法分析

4.1 收斂性分析

四階相關峭度的變化趨勢可以利用反卷積輸出的增量來進行考查，進而可求解出四階相關峭度反卷積算法的收斂條件，分析該算法的收斂情況。設yi+1(k)=(1+τ)yi(k) ，其 中τ是 增 量 因 子，且0<τ<1。將Ci+1(T)在yi(k)處按照泰勒級數展開得：

對上式中的微分項求解可得到：

結合上式，可以得到：

因為0<ρ<1，y1(k)>0，可以得到ρ>0，又因為A-B的跡決定了相關峭度的單調性，因此在反卷積逆濾波器的第i次迭代的過程中，如果有|A-B|≠0 ，則對于A-B的特征值λi滿足λi>0,i=1,2,…,n。 根 據 tr(A-B)>0 可 以 推 得ΔCi(T)>0，所以四階相關峭度函數為單調遞增函數。

設終止條件為φ，φ>0，在經過有限次的迭代之后，ΔCi(T) 達到迭代終止條件，即0<ΔCi(T)<φ。此時，四階相關峭度Ci+1(T)有最大值，所對應得逆濾波器迭代解Wp(k) 為最優解，此時算法收斂，收斂條件可以表示為

4.2 穩定性分析

分析M4CKD 的收斂性和收斂速度可知，當A-B為奇異矩陣，即其特征值λi>0,i=1,2,…,n時，最大四階相關峭度反卷積算法收斂。考慮A-B的跡，可以得：

即滿足上述條件時，四階相關峭度反卷積算法穩定，且此時AGV 行駛過程中的混合信號被盲提取。

5 算法驗證

此實驗使用的AGV包含8位磁導航傳感器，實驗平臺如圖1 所示。AGV 小車沿著已鋪設的軌道運行，在運行過程中，當磁導航傳感器感應到地面磁條的信號和野點信號時，通過模擬前端會輸出磁條的位置偏移量信息，進而對電機進行差速控制驅動，從而保證AGV能沿著預設軌道進行無偏行駛。

圖3 磁導航野點識別實驗平臺

輸入一幀混合觀測信號，仿真后將得到輸出信號，逆濾波器的單位沖擊響應和算法的迭代結果。設置算法迭代次數為20 次，濾波器的單位抽樣數為30，采樣周期T為5。仿真結果如下所示。

圖4是含有噪聲的輸入信號，根據該圖可以看出，在信號幅值處出現3 個波峰，其中波峰最高點對信號的影響最大，此處是引起AGV 行駛軌跡嚴重偏移閾值的主要原因。

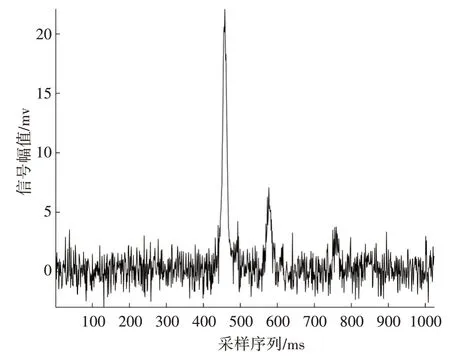
圖4 加性噪聲輸入信號

根據圖5 可以看出波峰中帶有的噪聲信號和其余部位帶有的噪聲信號經過逆濾波器之后被濾除，恢復出的源信號相較于之前的帶有噪聲的信號，信噪比更好，變得更加平滑。

圖5 信號經逆濾波器后的輸出

圖6表示的是混合信號經過采樣周期為5的逆濾波器單位響應，該單位響應的圖像類似于正弦函數。其幅度范圍大概在-0.15~+0.3之間。

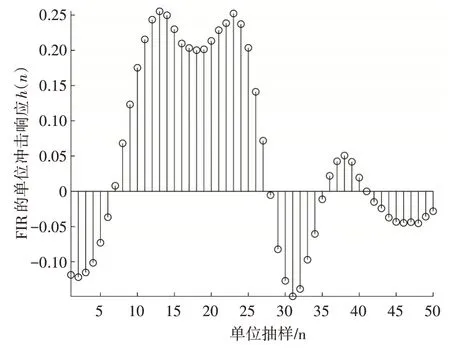
圖6 逆濾波器的單位響應

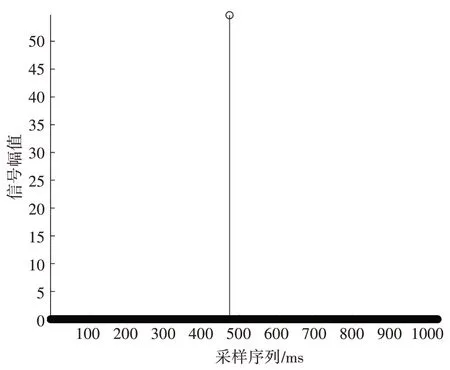
圖7 峰值提取

根據信號經過逆濾波器的輸出，我們可以提取出最大峰值，通過仿真結果可以得出，信號在x=491處被提取，其幅值為53.7187。

圖8是相關峭度與迭代次數的關系，迭代次數在1~6 之間相關峭度在逐漸增大，收斂速度非常快，當迭代次數達到6 次以后，相關峭度達到最大值，此時反卷積算法收斂并且趨于穩定，且盲提取誤差達到了9e-4，算法終止迭代。

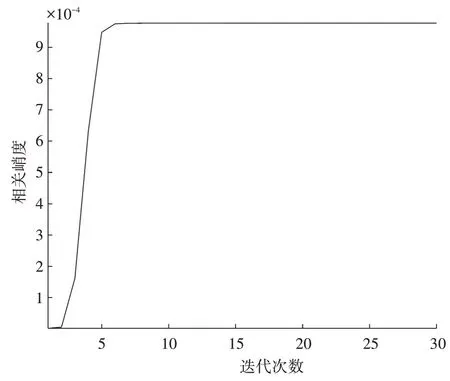
圖8 相關峭度與迭代次數

根據圖4 和圖5 可以看出，在經過逆濾波器之后，輸出的信號的幅值都有了提高，主要是因為濾波器的系數所產生的影響，當β越小時，y(k)就越大。因為本文主要是對包含異常點的信號進行盲提取后恢復出源信號，并且濾除其中的噪聲。我們在對峰值檢測時，檢測的是其位移，所以可以忽略幅值變化，其并不會對實驗結果產生影響。在進行仿真實驗時，如果調整噪聲參數，迭代的次數也會發生變化，當調整了高斯白噪聲的功率大小，并進行仿真實驗時，實驗結果如表1所示。

表1 高斯噪聲參數與迭代次數的關系

經過多次實驗仿真后，可以發現調整噪聲參數的大小與迭代次數之間是有一定關系的，隨著噪聲參數的值越大，迭代的次數會越大，收斂速度將會變慢，而且這些參數控制在0.3~1 之間的效果是較好的，之后的參數值繼續增大，混合信號的盲提取效果會變得很不理想，且收斂速度會更加緩慢。所以觀測序列的噪聲功率大小與算法的收斂速度有關，隨著噪聲功率越大，峭度的突變信息會越明顯，相關峭度的梯度值也就越大。

6 結語

在本文中，以四階峭度反卷積算法對AGV 行駛過程中所產生的混合信號進行識別和盲提取，通過對濾波器進行迭代，求出最優的迭代解，使AGV能夠在預設的軌道上準確平穩的運行。另外對算法的收斂性和穩定性做了論證推導，并對算法進行仿真分析。結果表明，該算法相比于傳統的算法，在收斂速度和穩定性方面都有了一定的提升，但在處理復雜度較高的信號時，例如多個波峰的情況下，由于波峰之間的濾波過程也會存在一定的影響，所以輸出的結果也會有所不同，該算法的性能有待加強。