基于虛擬同步機(jī)控制的新能源發(fā)電并網(wǎng)系統(tǒng)小干擾穩(wěn)定臨界短路比
康思偉,董文凱,郭詩(shī)然,孫紅軍,謝小榮
(1.中海油融風(fēng)能源有限公司,上海市 200335;2.電力系統(tǒng)及發(fā)電設(shè)備控制與仿真國(guó)家重點(diǎn)實(shí)驗(yàn)室(清華大學(xué)電機(jī)系),北京市 100084)
0 引 言
目前,基于矢量控制的電壓源型換流器(voltage source converter,VSC)在新能源發(fā)電領(lǐng)域具有廣泛應(yīng)用,其在為新能源發(fā)電提供快速靈活并網(wǎng)控制的同時(shí),也造成電力系統(tǒng)中旋轉(zhuǎn)慣量的降低,且難以在弱電網(wǎng)條件下保持良好的穩(wěn)定性。為應(yīng)對(duì)傳統(tǒng)VSC不具備旋轉(zhuǎn)慣量、無法有效為交流系統(tǒng)提供頻率和電壓支撐的問題[1-3],2007年,德國(guó)勞斯克塔爾工業(yè)大學(xué)Beck教授率先提出虛擬同步機(jī)(virtual synchronous generator,VSG)的概念,即將同步發(fā)電機(jī)動(dòng)態(tài)方程引入換流器控制[1-6],使其可以模擬同步機(jī)的慣性和阻尼等輸出特性,具備為交流系統(tǒng)提供頻率和電壓支撐的能力。這一提法隨后在全球范圍內(nèi)得到廣泛關(guān)注與認(rèn)可。
除為交流系統(tǒng)提供頻率和電壓支撐外,近年來的研究表明,電壓控制型VSG可在弱電網(wǎng)甚至是極弱電網(wǎng)的條件下,保持良好的小干擾穩(wěn)定特性[4-13]。文獻(xiàn)[4-5]針對(duì)基于VSG的雙饋風(fēng)機(jī)并網(wǎng)系統(tǒng),通過模式分析發(fā)現(xiàn),在弱電網(wǎng)甚至是極弱電網(wǎng)的條件下,VSG的振蕩模式仍具有較好的阻尼特性,系統(tǒng)具備在小干擾作用下保持良好運(yùn)行穩(wěn)定性的能力。文獻(xiàn)[6-13]基于阻抗模型,分析了VSG換流器并網(wǎng)系統(tǒng)在弱電網(wǎng)與極弱電網(wǎng)條件下的小干擾穩(wěn)定性,發(fā)現(xiàn)在短路比(short circuit ratio,SCR)不斷減小,甚至是接近于1的情況下,阻抗矩陣特征值的奈奎斯特曲線仍與(-1,0)之間保持一定距離,即系統(tǒng)仍具有一定的穩(wěn)定裕度[6-13]。考慮到對(duì)于傳統(tǒng)VSC并網(wǎng)系統(tǒng),大量理論研究與工程實(shí)踐都表明,系統(tǒng)在弱電網(wǎng)或極弱電網(wǎng)的條件下容易出現(xiàn)小干擾穩(wěn)定性問題[14-18],因此,VSG可能成為應(yīng)對(duì)弱電網(wǎng)條件下電能變換需求的有效解決方案。
但是,文獻(xiàn)[19-20]進(jìn)一步指出VSG更適合在弱電網(wǎng)條件下運(yùn)行,反而不適合強(qiáng)電網(wǎng)。文獻(xiàn)[21-22]基于線性化狀態(tài)空間模型,分析了VSG換流器并網(wǎng)系統(tǒng)小干擾穩(wěn)定性,發(fā)現(xiàn)隨交流電網(wǎng)強(qiáng)度提高,VSG振蕩模式在復(fù)平面上向右移動(dòng),造成系統(tǒng)小干擾穩(wěn)定性降低。文獻(xiàn)[23]基于阻抗模型,分析了VSG經(jīng)串補(bǔ)線路并網(wǎng)系統(tǒng)的小干擾穩(wěn)定性,發(fā)現(xiàn)隨串補(bǔ)度提高,系統(tǒng)穩(wěn)定性降低。在此,需要補(bǔ)充說明的是,當(dāng)前VSG可分為電壓控制型和電流控制型兩類,對(duì)弱電網(wǎng)條件的良好適應(yīng)性是針對(duì)電壓控制型VSG而言[8],文獻(xiàn)[21-23]中的結(jié)論也是基于僅具有電壓控制環(huán)的VSG并網(wǎng)系統(tǒng)獲得的。在以上研究的基礎(chǔ)上,為有效保障系統(tǒng)穩(wěn)定性、充分發(fā)揮此類VSG對(duì)弱電網(wǎng)的良好適應(yīng)性與為交流系統(tǒng)提供頻率和電壓支撐的能力,本文進(jìn)一步探討與明確考慮不同電網(wǎng)強(qiáng)度影響的VSG并網(wǎng)系統(tǒng)小干擾穩(wěn)定性判定方法以及系統(tǒng)臨界穩(wěn)定條件,為未來VSG并網(wǎng)系統(tǒng)規(guī)劃提供參考和借鑒。
為此,本文首先建立VSG并網(wǎng)系統(tǒng)小信號(hào)模型,并將其整理為兩輸入兩輸出單位負(fù)反饋系統(tǒng)的表示形式。然后,基于廣義奈奎斯特判據(jù),提出一種考慮不同電網(wǎng)強(qiáng)度的VSG并網(wǎng)系統(tǒng)小干擾穩(wěn)定性判定方法,定義系統(tǒng)小干擾穩(wěn)定臨界短路比(critical short circuit ratio,CSCR)。最后通過仿真算例,驗(yàn)證所提方法的有效性。
1 虛擬同步機(jī)并網(wǎng)系統(tǒng)小信號(hào)模型
VSG并網(wǎng)系統(tǒng)示意如圖1所示。其中,VSG的動(dòng)態(tài)可描述為[8]:
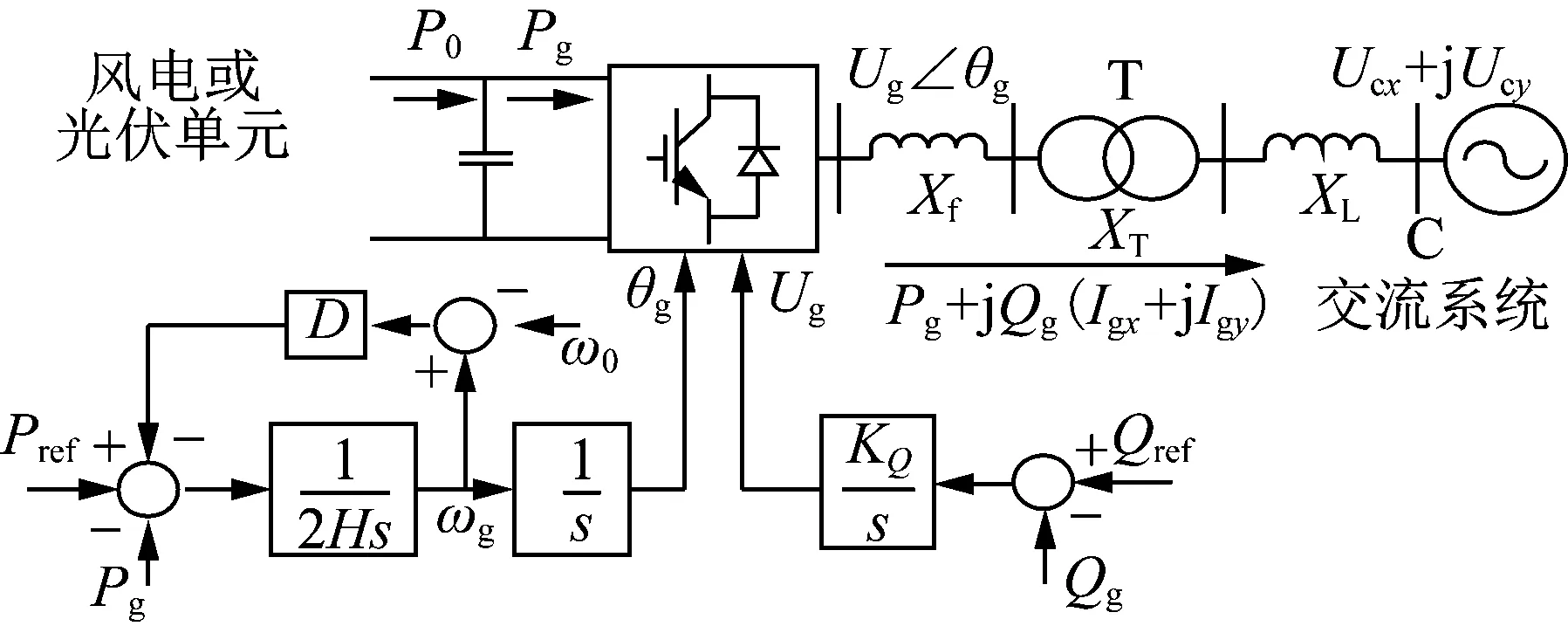
圖1 VSG并網(wǎng)系統(tǒng)示意圖Fig.1 A grid-connected VSG system
(1)
(2)
式中:ωg為VSG虛擬角頻率;ω0為系統(tǒng)額定角頻率;Ug、θg分別為VSG輸出電壓幅值和相角;H、D、KQ分別為VSG慣性常數(shù)、阻尼系數(shù)和無功控制器增益系數(shù);Pref、Qref分別為VSG輸出有功和無功的參考值;Pg、Qg為VSG輸出有功和無功功率;Ugx、Ugy為交流電網(wǎng)公共x-y坐標(biāo)系下VSG端x軸和y軸電壓。
Pg+jQg=(Ugx+jUgy)(Igx-jIgy)
(3)
式中:Igx、Igy表示交流電網(wǎng)公共x-y坐標(biāo)系下VSG端x軸和y軸的輸出電流。
將式(1)—(3)線性化并寫為狀態(tài)空間的表示形式:
(4)
式中:ΔXg=[ΔωgΔθgΔUg]T;ΔIg=[ΔIgxΔIgy]T;ΔUg=[ΔUgxΔUgy]T;Ag=
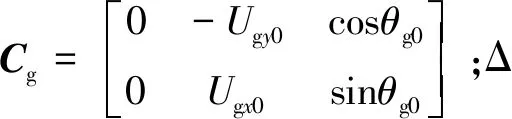
圖1中:Xf為濾波器電抗;XT為升壓變壓器電抗;XL為連接線路電抗。令XE=Xf+XT+XL表示VSG與交流系統(tǒng)間連接系統(tǒng)總電抗,則有
(5)
式中:Ucx、Ucy表示交流電網(wǎng)公共x-y坐標(biāo)系下,圖1中母線C的電壓。
將式(5)線性化并寫為狀態(tài)空間的表示形式:
(6)
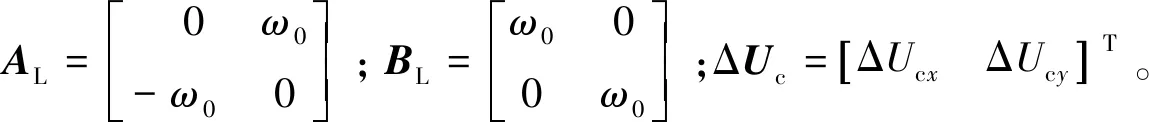
由式(4)和式(6),可得圖1所示VSG并網(wǎng)系統(tǒng)的線性化狀態(tài)空間模型:
(7)

由式(4)可得VSG小信號(hào)傳遞函數(shù)模型為:
ΔUg=G(s)ΔIg
(8)
式中:G(s)=Cg(sI3-Ag)-1Bg,I3為3×3單位矩陣。
將式(6)寫為傳遞函數(shù)的形式:
(9)
式中:H(s)=(sI2-AL)-1BL,I2為2×2單位矩陣。
由式(8)和式(9)可知,圖1所示的VSG并網(wǎng)系統(tǒng)小信號(hào)模型可表示為圖2所示的形式;VSG并網(wǎng)系統(tǒng)的小信號(hào)傳遞函數(shù)模型如式(10)所示。
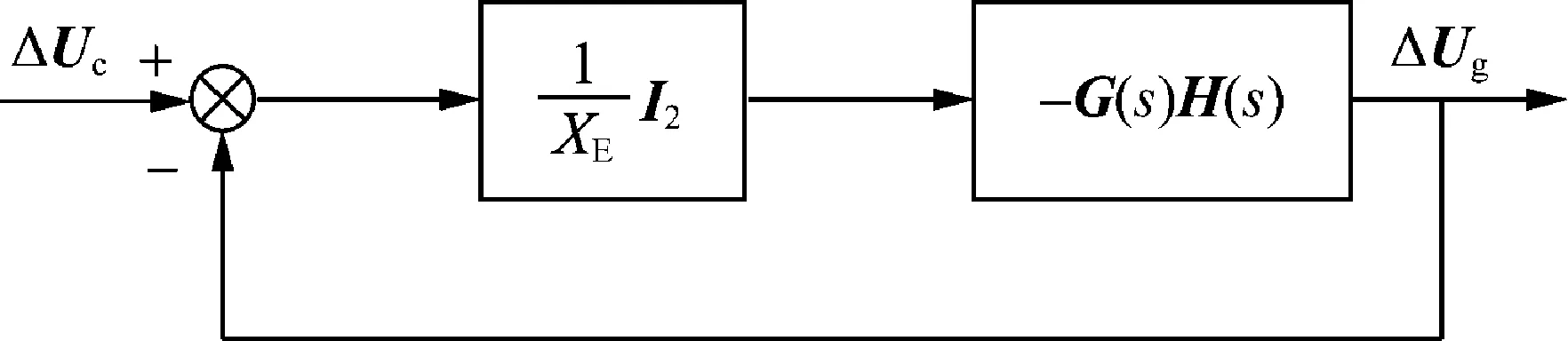
圖2 VSG并網(wǎng)系統(tǒng)小信號(hào)模型Fig.2 Small-signal model of a grid-connected VSG system
ΔUg=N(s)ΔUc
(10)
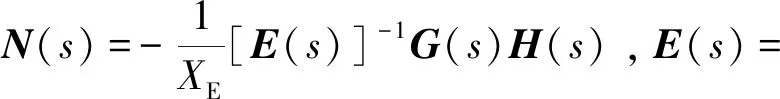
2 基于廣義奈奎斯特判據(jù)的虛擬同步機(jī)并網(wǎng)系統(tǒng)小干擾穩(wěn)定臨界短路比
第1節(jié)給出了VSG并網(wǎng)系統(tǒng)小信號(hào)模型,本節(jié)將在此基礎(chǔ)上探討考慮不同電網(wǎng)強(qiáng)度影響的系統(tǒng)小干擾穩(wěn)定性判定方法與臨界穩(wěn)定條件。
2.1 虛擬同步機(jī)并網(wǎng)系統(tǒng)短路比的定義
交流電網(wǎng)強(qiáng)度通常采用VSG并網(wǎng)點(diǎn)的短路比衡量,具體到圖1所示系統(tǒng),根據(jù)文獻(xiàn)[24],其短路比σSCR可表示為:
(11)
式中:S表示VSG額定容量標(biāo)幺值。SCR越小,交流電網(wǎng)強(qiáng)度越弱,SCR的取值為2~3時(shí),為弱電網(wǎng);SCR小于2時(shí),為極弱電網(wǎng)[16-17]。在此需要作進(jìn)一步說明的是,對(duì)于僅具有電壓控制環(huán)的VSG而言,可將VSG端口濾波電抗看作連接系統(tǒng)的一部分,并將其計(jì)入系統(tǒng)SCR中[24];而對(duì)于具有矢量電流控制環(huán)節(jié)的并網(wǎng)換流器而言,濾波電抗應(yīng)作為換流器的一部分而不能考慮到短路比當(dāng)中。
2.2 不同電網(wǎng)強(qiáng)度下VSG并網(wǎng)系統(tǒng)小干擾穩(wěn)定性判定方法
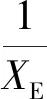
將回率矩陣F(s)的特征值記為R1(s)和R2(s),根據(jù)廣義奈奎斯特判據(jù),若系統(tǒng)開環(huán)穩(wěn)定,則可由R1(s)和R2(s)的奈奎斯特曲線是否逆時(shí)針包圍(-1,0)判斷圖2所示系統(tǒng)的穩(wěn)定性[25],具體說明如圖3所示。
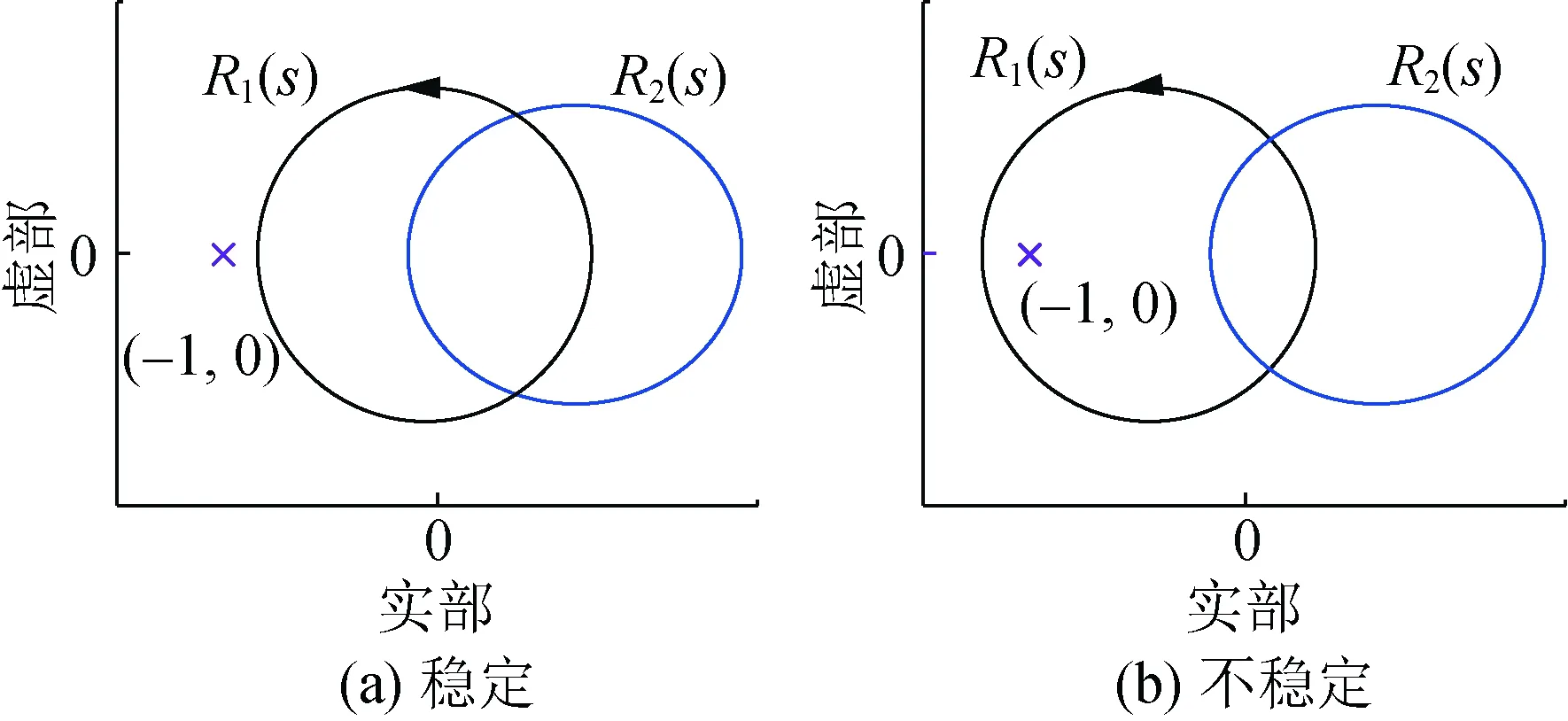
圖3 回率矩陣特征值的奈奎斯特曲線Fig.3 Nyquist plots of eigenvalues of return ratio matrix
若矩陣-G(s)H(s)的特征值為λ1(s)和λ2(s),則有λ1(s)=XER1(s)和λ2(s)=XER2(s)。因此,也可根據(jù)λ1(s)和λ2(s)的奈奎斯特曲線是否逆時(shí)針包圍(-XE,0)來判斷圖2所示系統(tǒng)的穩(wěn)定性,具體說明如圖4所示。
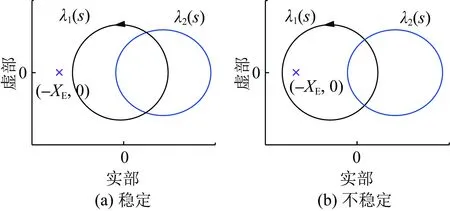
圖4 矩陣-G(s)H(s)特征值的奈奎斯特曲線1Fig.4 Nyquist plot 1 of eigenvalues of -G(s)H(s)
為便于說明問題,圖4給出的奈奎斯特曲線的形式較為簡(jiǎn)單,實(shí)際上,還可能出現(xiàn)λ1(s)和λ2(s)的奈奎斯特曲線順時(shí)針包圍(-XE,0)的情況,此時(shí)應(yīng)考慮與順時(shí)針包圍的曲線抵消后,(-XE,0)是否會(huì)被λ1(s)和λ2(s)的奈奎斯特曲線“凈”逆時(shí)針包圍[25],來判斷系統(tǒng)穩(wěn)定性。具體說明如圖5所示,圖5(a)中,(-XE,0)被順時(shí)針和逆時(shí)針包圍的圈數(shù)均為1,凈逆時(shí)針包圍圈數(shù)為0,系統(tǒng)穩(wěn)定;圖5(b)中,凈逆時(shí)針包圍圈數(shù)為1,系統(tǒng)失穩(wěn)。
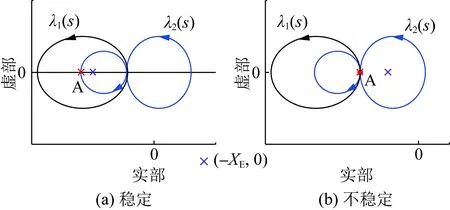
圖5 矩陣-G(s)H(s)特征值的奈奎斯特曲線2Fig.5 Nyquist plot 2 of eigenvalues of -G(s)H(s)
若定義奈奎斯特曲線由上向下穿過實(shí)軸為“正穿越”,且與實(shí)軸的交點(diǎn)為“正穿越點(diǎn)”,由下向上穿過實(shí)軸為負(fù)穿越,與實(shí)軸的交點(diǎn)為“負(fù)穿越點(diǎn)”,顯然,正穿越對(duì)應(yīng)逆時(shí)針閉合曲線的開始或順時(shí)針閉合曲線的結(jié)束,負(fù)穿越恰好與之相反。若某一穿越點(diǎn)及其左側(cè)所有穿越點(diǎn)中,正穿越點(diǎn)數(shù)多于負(fù)穿越點(diǎn)數(shù),則該穿越點(diǎn)可稱為“凈正穿越點(diǎn)”。由此:
1)若實(shí)軸上(-XE,0)左側(cè)存在穿越點(diǎn),且左側(cè)距(-XE,0)最近的穿越點(diǎn)為凈正穿越點(diǎn),則(-XE,0)被奈奎斯特曲線逆時(shí)針包圍,系統(tǒng)失穩(wěn);
2)若有穿越點(diǎn)與(-XE,0)重合,則系統(tǒng)臨界穩(wěn)定;
3)若上述情況1)和2)均未出現(xiàn),則系統(tǒng)穩(wěn)定。
以圖5為例,圖5(a)中A點(diǎn)及其左側(cè)有一個(gè)負(fù)穿越點(diǎn)和一個(gè)正穿越點(diǎn),A點(diǎn)非凈正穿越點(diǎn),系統(tǒng)穩(wěn)定;圖5(b)中,A點(diǎn)及其左側(cè)有3個(gè)正穿越點(diǎn)和2個(gè)負(fù)穿越點(diǎn),A點(diǎn)為凈正穿越點(diǎn),系統(tǒng)失穩(wěn)(藍(lán)色曲線在A點(diǎn)處有2次正穿越、黑色曲線有1次負(fù)穿越,此處應(yīng)記為2個(gè)正穿越點(diǎn)和1個(gè)負(fù)穿越點(diǎn))。
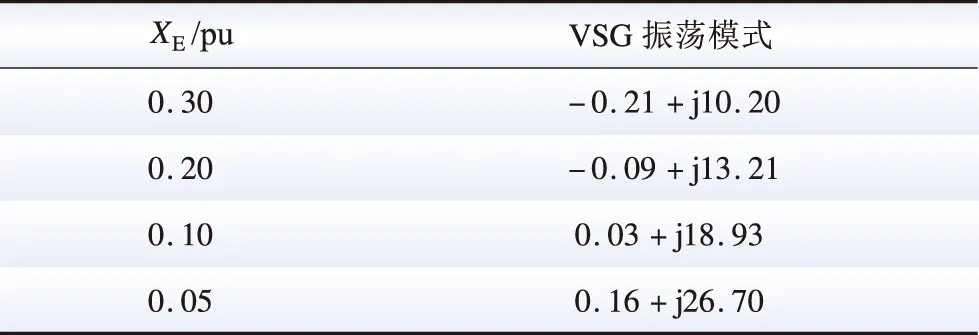
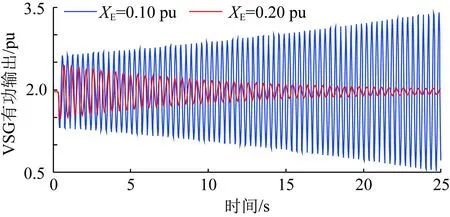
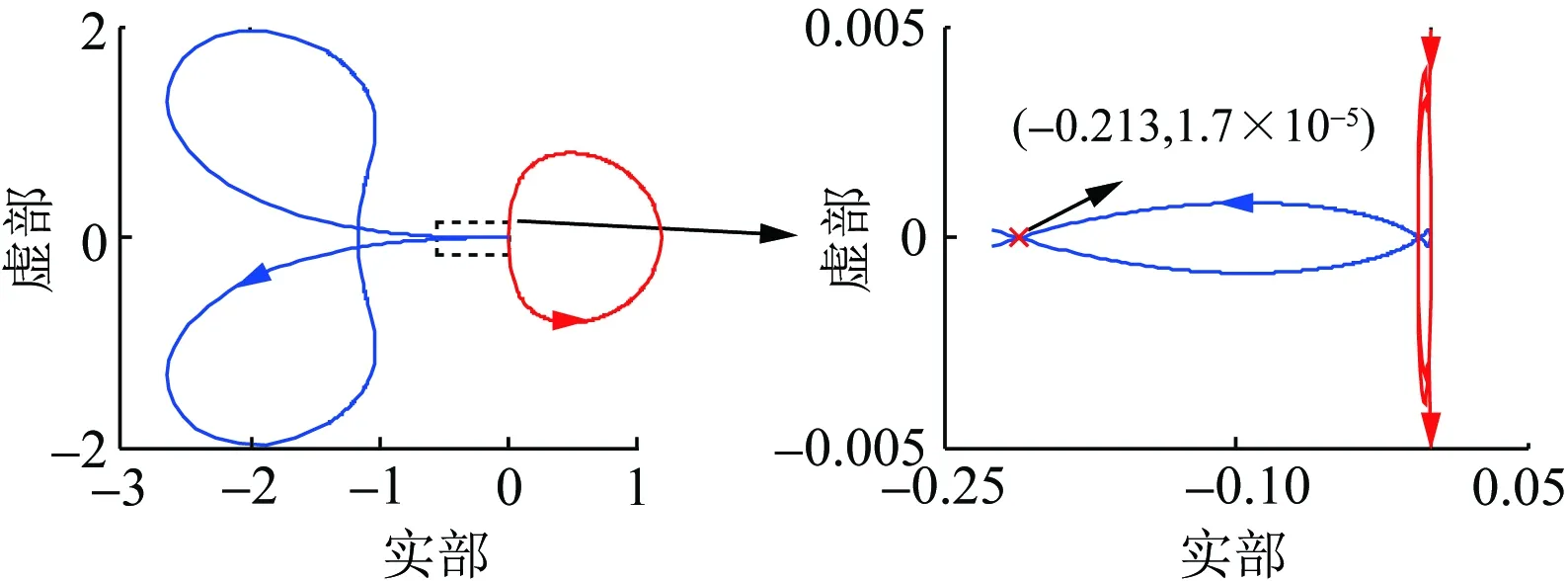
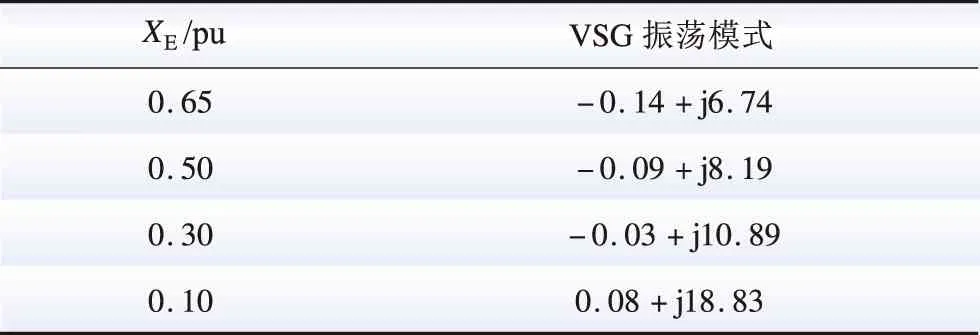
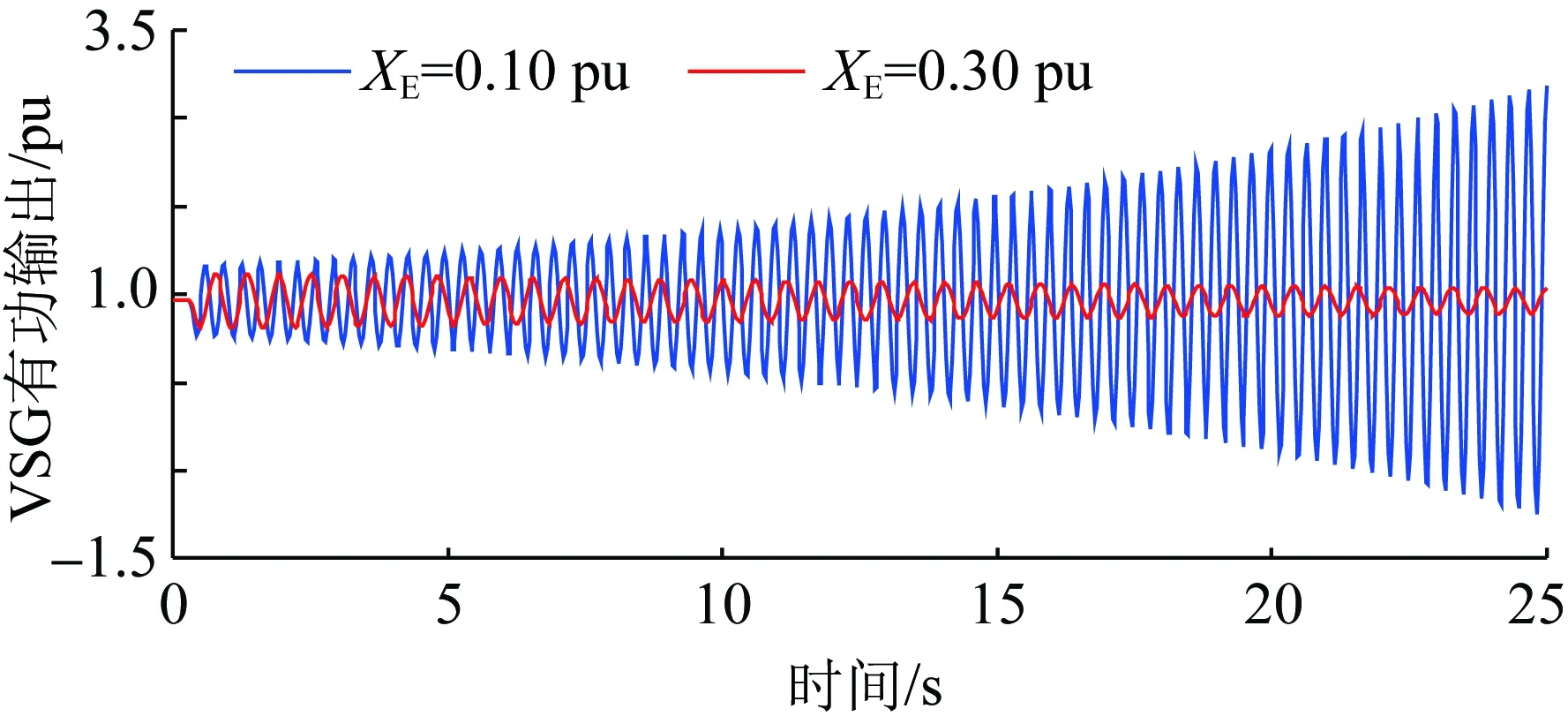
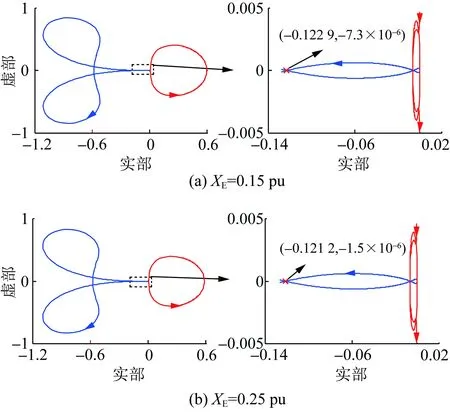
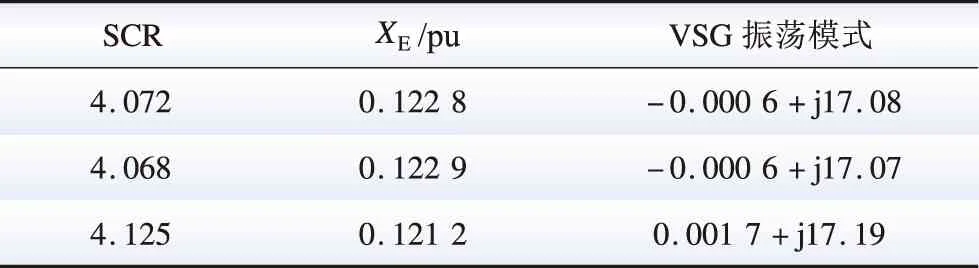
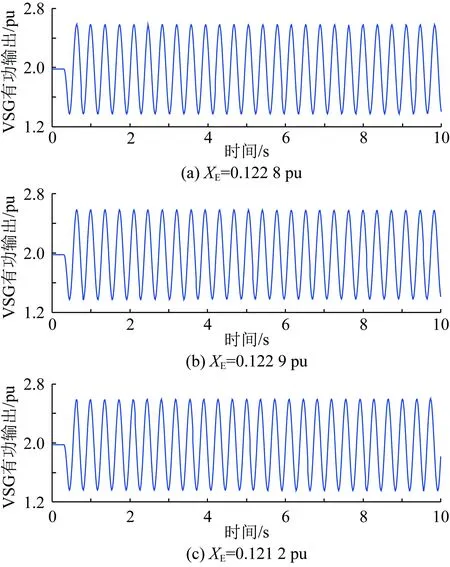
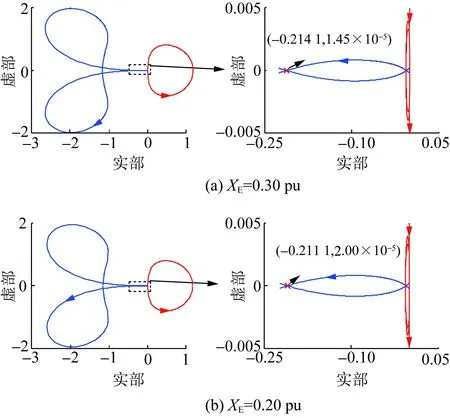
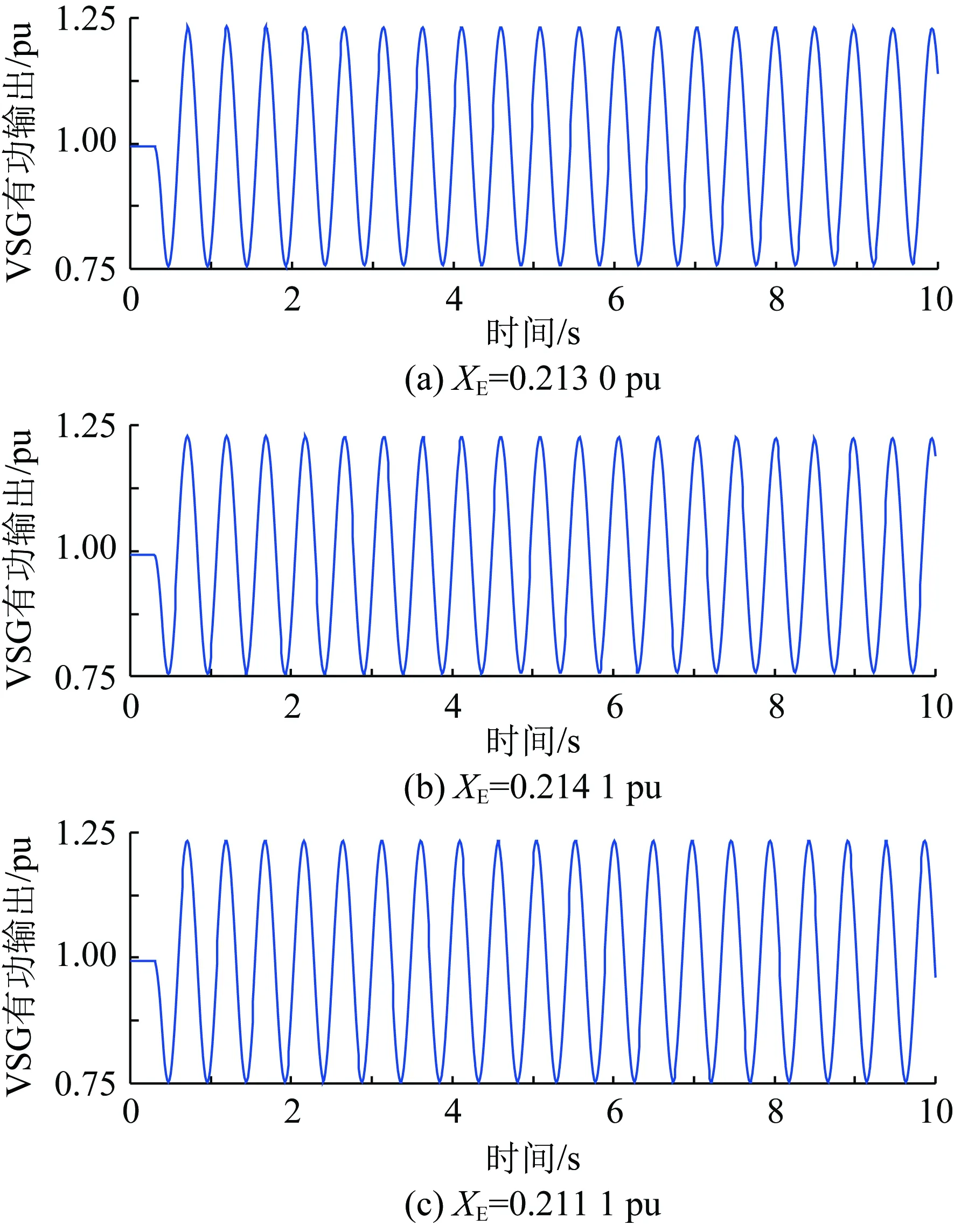
由式(4)、式(6)、式(8)和式(9),對(duì)于一給定的VSG,G(s)和H(s)的表達(dá)式與XE無關(guān),即λ1(s)和λ2(s)奈奎斯特曲線的繪制結(jié)果基本不受XE變化的影響。在XE變化的過程中,(-XE,0)沿實(shí)軸移動(dòng),其左側(cè)實(shí)軸被λ1(s)和λ2(s)奈奎斯特曲線穿越的情況可能也會(huì)相對(duì)發(fā)生變化,從而造成系統(tǒng)穩(wěn)定性的變化。結(jié)合此前的分析,沿實(shí)軸由左向右,一個(gè)凈正穿越點(diǎn)Ai(ai,0)和此后與其相鄰的非凈正穿越點(diǎn)Bi(bi,0)之間構(gòu)成一個(gè)失穩(wěn)區(qū)間φi={(x,0)|ai 圖6 XE減小造成VSG并網(wǎng)系統(tǒng)穩(wěn)定性變化圖示說明Fig.6 Illustration on the stability variation of the grid-connected VSG system due to the decrease of XE 綜上,可獲得一種判定給定VSG在不同電網(wǎng)強(qiáng)度下構(gòu)成并網(wǎng)系統(tǒng)小干擾穩(wěn)定性的方法如下: 1)根據(jù)式(4)、式(5)、式(8)和式(9),建立傳遞函數(shù)矩陣G(s)和H(s),并繪制矩陣-G(s)H(s)特征值的奈奎斯特曲線; 2)根據(jù)奈奎斯特曲線對(duì)實(shí)軸負(fù)半軸的穿越情況,確定ξ上的失穩(wěn)區(qū)間φ1i(i=1,2,…,m1,m1為區(qū)間ξ內(nèi)失穩(wěn)區(qū)間的個(gè)數(shù)); 3)當(dāng)(-XE,0)∈φ1i時(shí),系統(tǒng)失穩(wěn);當(dāng)(-XE,0)與區(qū)間ξ內(nèi)的穿越點(diǎn)重合時(shí),系統(tǒng)臨界穩(wěn)定。 采用以上方法,對(duì)于一個(gè)VSG,在給定運(yùn)行狀態(tài)下,僅需一次繪制系統(tǒng)的奈奎斯特曲線,便可獲得使VSG并網(wǎng)系統(tǒng)小干擾失穩(wěn)的XE的取值區(qū)間。在未來,VSG生產(chǎn)廠家可考慮選擇幾種典型運(yùn)行狀態(tài),給出圖6所示的VSG并網(wǎng)系統(tǒng)奈奎斯特曲線及失穩(wěn)區(qū)間,這一信息對(duì)于VSG并網(wǎng)系統(tǒng)設(shè)備選擇和規(guī)劃具有很好的借鑒和指導(dǎo)意義。 考慮到現(xiàn)有研究表明,對(duì)于圖1所示的電壓控制型VSG,其更適合于弱電網(wǎng)條件,反而不適合強(qiáng)電網(wǎng)[19-22]。文獻(xiàn)[21]和[22]中進(jìn)一步表明,隨XE減小,VSG振蕩模式在復(fù)平面上向右移動(dòng),系統(tǒng)小干擾穩(wěn)定性降低。XE=0 pu時(shí)VSG并網(wǎng)系統(tǒng)小干擾穩(wěn)定性推導(dǎo)見附錄A,根據(jù)附錄A中的推導(dǎo),當(dāng)XE=0 pu時(shí),系統(tǒng)小干擾失穩(wěn),即VSG直接接入無窮大電網(wǎng)時(shí)失穩(wěn),對(duì)此,文獻(xiàn)[8]和[23]基于阻抗模型,得到相同的結(jié)論。因此,通常來講,應(yīng)存在一個(gè)臨界電網(wǎng)強(qiáng)度或臨界SCR,在系統(tǒng)實(shí)際SCR超過該臨界SCR時(shí),系統(tǒng)小干擾失穩(wěn)。 與上述分析對(duì)應(yīng),在區(qū)間ξ內(nèi)存在一個(gè)凈正穿越點(diǎn)A(a,0),A點(diǎn)與原點(diǎn)之間構(gòu)成一個(gè)失穩(wěn)區(qū)間,在XE減小的過程中,(-XE,0)沿實(shí)軸向原點(diǎn)移動(dòng),不斷靠近A點(diǎn),系統(tǒng)小干擾穩(wěn)定裕度降低,(-XE,0)與A點(diǎn)重合時(shí),系統(tǒng)臨界穩(wěn)定,(-XE,0)移動(dòng)至A點(diǎn)右側(cè)時(shí),系統(tǒng)小干擾失穩(wěn)。據(jù)此,可獲得VSG并網(wǎng)系統(tǒng)小干擾穩(wěn)定臨界短路比的定義與確定方法如下: 令VSG處于額定運(yùn)行狀態(tài),根據(jù)式(4)、式(5)、式(8)和式(9),建立矩陣-G(s)H(s),并繪制其特征值的奈奎斯特曲線,得到區(qū)間ξ內(nèi)的凈正穿越點(diǎn)A(a,0);對(duì)應(yīng)的VSG并網(wǎng)系統(tǒng)小干擾穩(wěn)定臨界短路比(critical short circuit ration considering small-signal stability,CSCR_S)σCSCR_S為: (12) 在VSG處于額定運(yùn)行狀態(tài)時(shí),為確保VSG并網(wǎng)系統(tǒng)的小干擾穩(wěn)定性,系統(tǒng)實(shí)際SCR應(yīng)小于式(12)給出的CSCR_S,對(duì)此應(yīng)在VSG并網(wǎng)系統(tǒng)規(guī)劃階段重點(diǎn)考慮。 從本節(jié)的分析可以看出,隨著電網(wǎng)強(qiáng)度的提升(或SCR的增大),VSG并網(wǎng)系統(tǒng)小干擾穩(wěn)定性降低,當(dāng)實(shí)際SCR大小超過所得CSCR_S時(shí),系統(tǒng)失穩(wěn)。對(duì)于VSG控制的原理和模型,本文主要以圖1和式(1)、(2)所示的核心部分為例進(jìn)行介紹;理論上講,VSG中應(yīng)引入類似于傳統(tǒng)同步機(jī)中的調(diào)差環(huán)節(jié),但是此時(shí)VSG的小信號(hào)模型仍能表示為式(4)所示形式,因此,本節(jié)所提CSCR_S的求解方法,在考慮VSG控制中的調(diào)差等更為細(xì)節(jié)的環(huán)節(jié)時(shí)依然適用。此外,VSG參數(shù)不同,其并網(wǎng)系統(tǒng)的CSCR_S的大小也不相同。由于VSG并網(wǎng)系統(tǒng)數(shù)學(xué)模型的復(fù)雜性,對(duì)于控制參數(shù)和調(diào)差環(huán)節(jié)對(duì)系統(tǒng)小干擾穩(wěn)定性的影響,當(dāng)前尚無法通過類似于圖2所示形式直觀地反映出來,須對(duì)具體案例進(jìn)行具體分析。本文主要針對(duì)給定VSG的小干擾穩(wěn)定臨界短路比的求解,對(duì)于控制參數(shù)、運(yùn)行點(diǎn)和調(diào)差環(huán)節(jié)等部分對(duì)系統(tǒng)CSCR_S的影響機(jī)理和規(guī)律,則還須進(jìn)一步研究,本文不做討論。 本節(jié)采用圖1所示系統(tǒng),驗(yàn)證第2節(jié)所提小干擾穩(wěn)定性判定方法和CSCR_S的有效性,VSG參數(shù)為:D=0.6、H=5、KQ=0.4,仿真軟件采用Matlab。 本節(jié)分別在VSG穩(wěn)態(tài)功率輸出S0為2.0 pu和1.0 pu(功率因數(shù)均為0.98)的情況下,分析XE變化時(shí)VSG并網(wǎng)系統(tǒng)的小干擾穩(wěn)定性,驗(yàn)證2.2節(jié)所提小干擾穩(wěn)定性判定方法的有效性。 對(duì)于S0=2.0 pu的情況,(-XE,0)可能的運(yùn)動(dòng)區(qū)間為ξ={(x,0)|-0.5 圖7 S0=2.0 pu時(shí)的奈奎斯特曲線(算例1)Fig.7 Nyquist plots when S0=2.0 pu (case 1) 然后,在XE由0.30 pu減小至0.05 pu的過程中,建立式(7)所示VSG并網(wǎng)系統(tǒng)線性化狀態(tài)空間模型,并計(jì)算矩陣A的特征值,得到VSG振蕩模式如表1所示。由表1可以看出,隨著XE的減小,振蕩模式阻尼減小。當(dāng)XE<0.122 8 pu時(shí),系統(tǒng)小干擾失穩(wěn)。 表1 S0=2.0 pu時(shí)VSG振蕩模式計(jì)算結(jié)果(算例1)Table 1 Computational results of oscillation modes of the VSG when S0=2.0 pu (case 1) 最后,對(duì)算例系統(tǒng)小干擾穩(wěn)定性進(jìn)行非線性仿真分析。仿真中的擾動(dòng)設(shè)置為:0.2 s時(shí),輸入VSG的有功功率P0降低20%,并于0.1 s內(nèi)恢復(fù)。仿真結(jié)果如圖8所示,可以看出,XE=0.20 pu時(shí),系統(tǒng)穩(wěn)定,XE=0.10 pu時(shí),系統(tǒng)失穩(wěn),與此前基于線性化模型所得結(jié)論一致。 圖8 S0=2.0 pu時(shí)非線性仿真結(jié)果(算例1)Fig.8 Non-linear simulation results when S0=2.0 pu (case 1) 對(duì)于S0=1.0 pu的情況,(-XE,0)的運(yùn)動(dòng)區(qū)間為ξ={(x,0)|-1 圖9 S0=1.0 pu時(shí)的奈奎斯特曲線(算例1)Fig.9 Nyquist plots when S0=1.0 pu (case 1) 然后,在XE由0.65 pu減小至0.10 pu的過程中,建立式(7)所示VSG并網(wǎng)系統(tǒng)線性化模型,并計(jì)算矩陣A的特征值,得到VSG振蕩模式如表2所示。由表2可以看出,隨著XE的減小,振蕩模式阻尼降低。當(dāng)XE<0.213 pu時(shí),系統(tǒng)小干擾失穩(wěn)。 表2 S0=1.0 pu時(shí)VSG振蕩模式計(jì)算結(jié)果(算例1)Table 2 Computational results of oscillation modes of the VSG when S0=1.0 pu (case 1) 最后,對(duì)系統(tǒng)小干擾穩(wěn)定性進(jìn)行非線性仿真分析。仿真中擾動(dòng)設(shè)置同S0=2.0 pu的情況,仿真結(jié)果如圖10所示,可以看出,XE=0.30 pu時(shí),系統(tǒng)穩(wěn)定,XE=0.10 pu時(shí),系統(tǒng)失穩(wěn),與此前所得結(jié)論一致。 圖10 S0=1.0 pu時(shí)非線性仿真結(jié)果(算例1)Fig.10 Non-linear simulation results when S0=1.0 pu (case 1) 本節(jié)分別以VSG額定容量為2.0 pu和1.0 pu兩種情況為例,驗(yàn)證2.3節(jié)給出的VSG并網(wǎng)系統(tǒng)小干擾穩(wěn)定臨界短路比的有效性。 對(duì)于VSG額定容量為2.0 pu的情況,設(shè)定S0=2.0 pu,功率因數(shù)為0.98。由3.1節(jié)中圖7,系統(tǒng)小干擾穩(wěn)定臨界短路比為4.072。為進(jìn)一步驗(yàn)證2.3節(jié)定義的小干擾穩(wěn)定臨界短路比的有效性,分別在XE為0.15和0.25 pu的情況下,建立VSG的小信號(hào)模型,并繪制矩陣-G(s)H(s)特征值的奈奎斯特曲線,所得結(jié)果如圖11所示。可以看出,系統(tǒng)小干擾穩(wěn)定臨界短路比分別為4.068和4.125。 圖11 S0=2.0 pu時(shí)的奈奎斯特曲線(算例2)Fig.11 Nyquist plots when S0=2.0 pu (case 2) 然后,在系統(tǒng)實(shí)際SCR等于以上所得小干擾穩(wěn)定臨界短路比的情況下,建立VSG并網(wǎng)系統(tǒng)線性化模型,計(jì)算矩陣A的特征值,得到VSG振蕩模式如表3所示,可以看出,當(dāng)實(shí)際SCR等于小干擾穩(wěn)定臨界短路比時(shí),系統(tǒng)基本處于臨界穩(wěn)定狀態(tài),驗(yàn)證了小干擾穩(wěn)定臨界短路比的有效性。 表3 S0=2.0 pu時(shí)VSG振蕩模式計(jì)算結(jié)果(算例2)Table 3 Computational results of oscillation modes of the VSG when S0=2.0 pu (case 2) 此外,XE取不同值時(shí),以上所得小干擾穩(wěn)定臨界短路比數(shù)值也略有差異,這是由于,雖然VSG穩(wěn)態(tài)功率輸出恒定,XE取值不同,對(duì)圖1所示系統(tǒng)作穩(wěn)態(tài)潮流計(jì)算,所得VSG端電壓和輸出電流穩(wěn)態(tài)值不同,造成VSG小信號(hào)模型略有差異,矩陣-G(s)H(s)特征值的奈奎斯特曲線也有所不同,由此獲得的小干擾穩(wěn)定臨界短路比也略有差異。但是在VSG參數(shù)和輸出功率恒定的條件下,端電壓和輸出電流穩(wěn)態(tài)值差異造成的VSG小信號(hào)模型的差異不大,因此,XE取不同值時(shí),所得小干擾穩(wěn)定臨界短路比差異不大,且系統(tǒng)實(shí)際SCR等于小干擾穩(wěn)定臨界短路比時(shí),VSG并網(wǎng)系統(tǒng)基本在臨界穩(wěn)定狀態(tài)。 最后,在系統(tǒng)實(shí)際SCR等于所得小干擾穩(wěn)定臨界短路比時(shí),進(jìn)行非線性仿真分析。仿真中擾動(dòng)設(shè)置同3.1節(jié),所得結(jié)果如圖12所示,可以看出,當(dāng)實(shí)際SCR等于小干擾穩(wěn)定臨界短路比時(shí),系統(tǒng)基本處于小干擾臨界穩(wěn)定狀態(tài),驗(yàn)證了小干擾穩(wěn)定臨界短路比的有效性。 圖12 S0=2.0 pu時(shí)非線性仿真結(jié)果(算例2)Fig.12 Non-linear simulation results when S0=2.0 pu (case 2) 對(duì)于VSG額定容量為1.0 pu的情況,設(shè)定S0=1.0 pu,功率因數(shù)為0.98。由圖9可得,小干擾穩(wěn)定臨界短路比為4.695。以下進(jìn)一步給出XE為0.30和0.20 pu時(shí),矩陣-G(s)H(s)特征值的奈奎斯特曲線如圖13所示。由圖13可得系統(tǒng)小干擾穩(wěn)定臨界短路比分別為4.671和4.737。 圖13 S0=1.0 pu時(shí)的奈奎斯特曲線(算例2)Fig.13 Nyquist plots when S0=1.0 pu (case 2) 然后,在系統(tǒng)實(shí)際SCR等于以上所得小干擾穩(wěn)定臨界短路比的情況下,建立VSG并網(wǎng)系統(tǒng)線性化模型,計(jì)算矩陣A的特征值,得到VSG振蕩模式如表4所示,可以看出,當(dāng)實(shí)際SCR等于小干擾穩(wěn)定臨界短路比時(shí),系統(tǒng)基本處于臨界穩(wěn)定狀態(tài),驗(yàn)證了小干擾穩(wěn)定臨界短路比的有效性。 表4 S0=1.0 pu時(shí)VSG振蕩模式計(jì)算結(jié)果(算例2)Table 4 Computational results of oscillation modes of the VSG when S0=1.0 pu (case 2) 最后,在系統(tǒng)實(shí)際SCR等于所得小干擾穩(wěn)定臨界短路比時(shí),進(jìn)行非線性仿真分析。仿真中擾動(dòng)設(shè)置同3.1節(jié),所得結(jié)果如圖14所示,可以看出,當(dāng)實(shí)際SCR等于小干擾穩(wěn)定臨界短路比時(shí),系統(tǒng)基本處于小干擾臨界穩(wěn)定狀態(tài),驗(yàn)證了小干擾穩(wěn)定臨界短路比的有效性。 圖14 S0=1.0 pu時(shí)非線性仿真結(jié)果(算例2)Fig.14 Non-linear simulation results when S0=1.0 pu (case 2) 本文針對(duì)僅具有電壓控制環(huán)的VSG并網(wǎng)系統(tǒng),基于廣義奈奎斯特判據(jù),定義了系統(tǒng)小干擾穩(wěn)定臨界短路比,并得到了一種考慮電網(wǎng)強(qiáng)度影響的系統(tǒng)小干擾穩(wěn)定性判定方法。 1)建立了VSG并網(wǎng)系統(tǒng)小信號(hào)模型,并將其整理為兩輸入兩輸出單位負(fù)反饋系統(tǒng)的表示形式。 2)采用上述建模表示形式,基于廣義奈奎斯判據(jù),獲得了一種考慮電網(wǎng)強(qiáng)度影響的系統(tǒng)小干擾穩(wěn)定性判定方法,定義了系統(tǒng)小干擾穩(wěn)定臨界短路比。 3)通過仿真算例,驗(yàn)證了所提小干擾穩(wěn)定性判定方法和小干擾穩(wěn)定臨界短路比的有效性。 對(duì)于一個(gè)具體的VSG,在選定運(yùn)行狀態(tài)下,僅需一次繪制奈奎斯特曲線,便可獲得使VSG并網(wǎng)系統(tǒng)小干擾失穩(wěn)連接電抗的取值區(qū)間。這一信息對(duì)于未來VSG并網(wǎng)規(guī)劃具有很好的借鑒和指導(dǎo)意義。本文是基于僅具有電壓控制環(huán)結(jié)構(gòu)的VSG展開研究的,除此之外還有電流控制型等其他結(jié)構(gòu)的VSG。對(duì)于電網(wǎng)強(qiáng)度對(duì)其他VSG并網(wǎng)構(gòu)成系統(tǒng)小干擾穩(wěn)定性的影響和相關(guān)穩(wěn)定判據(jù),將在后續(xù)發(fā)表的文章中作進(jìn)一步報(bào)道。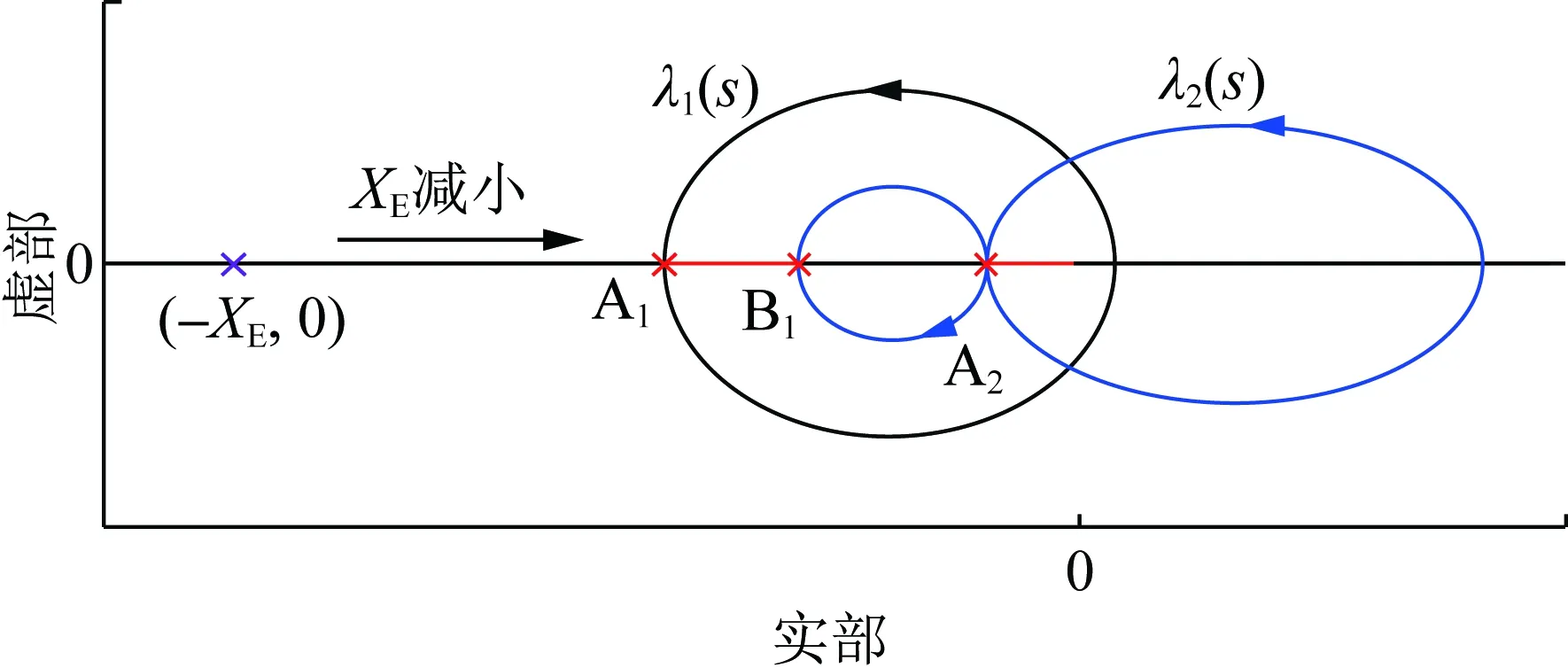
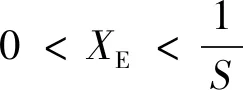
2.3 VSG并網(wǎng)系統(tǒng)小干擾穩(wěn)定臨界短路比
3 算例分析
3.1 算例1
3.2 算例2

4 結(jié) 論

