不確定規(guī)劃中循環(huán)可達(dá)狀態(tài)信息的維護(hù)*

張瀟妮 文中華，2 彭擎宇

（1.湘潭大學(xué)信息工程學(xué)院 湘潭 411105）（2.湖南工程學(xué)院計(jì)算機(jī)與通信學(xué)院 湘潭 411104）

1 引言

智能規(guī)劃的基礎(chǔ)模型通過圖來建立［1］，近年來，對(duì)智能規(guī)劃的建模從確定圖模型擴(kuò)展到不確定圖模型［2］。不確定規(guī)劃放寬以往經(jīng)典規(guī)劃的一些基本假設(shè)，使之更接近實(shí)際情況的解答，現(xiàn)已應(yīng)用到不少領(lǐng)域中。

在不確定規(guī)劃［3］中，有許多求解不確定規(guī)劃解［4～6］與一些復(fù)雜查詢的問題研究（如：蛋白質(zhì)分子之間是否有交互作用，找尋網(wǎng)絡(luò)安全中的不確定攻擊圖的攻擊路徑［7～8］等）。在求解與查詢過程中，由于狀態(tài)之間的可達(dá)信息缺乏，會(huì)有大量重復(fù)的搜索，因此，有不少學(xué)者在可達(dá)性查詢［9］研究取得重要成果，如：基于樹形結(jié)構(gòu)的可達(dá)性查詢［10～12］，利用矩陣的性質(zhì)求解狀態(tài)之間的可達(dá)性［13～15］等，基于區(qū)間樹的求解算法只能盡大可能地獲取節(jié)點(diǎn)之間的可達(dá)關(guān)系，不能良好地求解整個(gè)系統(tǒng)中的各個(gè)節(jié)點(diǎn)之間的可達(dá)關(guān)系。在動(dòng)態(tài)環(huán)境中，對(duì)狀態(tài)可達(dá)性的研究更多的是基于狀態(tài)之間的確定可達(dá)的操作，若是可達(dá)即為確定可達(dá)，否則為不可達(dá)，忽略了狀態(tài)之間的不確定可達(dá)，此外，對(duì)有向圖的要求大多是無環(huán)的。

在不確定規(guī)劃中，它考慮了每一個(gè)動(dòng)作效果的存在性，也就考慮了狀態(tài)之間的可達(dá)性的不確定性。本文通過矩陣來建立問題模型，充分考慮狀態(tài)之間的動(dòng)作執(zhí)行的不確定性，準(zhǔn)確表達(dá)狀態(tài)間的可達(dá)性（確定可達(dá)、不確定可達(dá)與不可達(dá)），提出了一種新的狀態(tài)可達(dá)關(guān)系的維護(hù)算法，對(duì)動(dòng)態(tài)環(huán)境下的不確定性動(dòng)作的存在變動(dòng)性所影響的狀態(tài)之間的可達(dá)關(guān)系進(jìn)行局部更新維護(hù)，適用于循環(huán)不確定系統(tǒng)中。該方法根據(jù)已有的信息可達(dá)矩陣和變更之后的不確定系統(tǒng)的鄰接矩陣的信息，重新進(jìn)行轉(zhuǎn)發(fā)，對(duì)可達(dá)矩陣進(jìn)行局部更新，取得新的狀態(tài)可達(dá)矩陣，避免重新求解。

2 相關(guān)定義

定義1：一個(gè)三元組可表示為規(guī)劃領(lǐng)域中的不確定的狀態(tài)轉(zhuǎn)換系統(tǒng)，即∑=＜S,A,γ＞其中：S是一個(gè)有限狀態(tài)集；A是一個(gè)有限動(dòng)作集；γ:S×A→2s是狀態(tài)轉(zhuǎn)移函數(shù)。

定義2：設(shè)∑=＜S,A,γ＞是一個(gè)不確定狀態(tài)轉(zhuǎn)移系統(tǒng)，從狀態(tài)si開始，執(zhí)行γ=(si,ax)之后，可能到達(dá)的狀態(tài)集合SL={s|s∈(sx,ax),s?{s1,s2,…,sn},1 ≤x≤n} 中的一個(gè)狀態(tài)，若si∈γ(sj,aj)(?i,i＜j)，則稱∑=＜S,A,γ＞為循環(huán)不確定狀態(tài)轉(zhuǎn)移系統(tǒng)s∈γ(sj,aj)(?i,i＜j)，否則為非循環(huán)不確定狀態(tài)轉(zhuǎn)移系統(tǒng)。

定義3：在一個(gè)不確定狀態(tài)轉(zhuǎn)移系統(tǒng)中，用函數(shù)d(s1,s2) 來表示s1和s2兩個(gè)狀態(tài)間的可達(dá)關(guān)系。可達(dá)關(guān)系定義如下：

當(dāng)狀態(tài)s1存在一條非循環(huán)路徑確定可達(dá)狀態(tài)s2時(shí)，則稱s1到s2確定可達(dá)，d(s1,s2)=1；

當(dāng)狀態(tài)s1存在一條路徑L并且s2∈SL時(shí)，則稱s1到s2不確定可達(dá)，d(s1,s2)=T；

當(dāng)狀態(tài)s1的任意一條路徑L都有s2?SL時(shí)，則稱s1到s2不可達(dá)，d(s1,s2)=0；

其中狀態(tài)自己到狀態(tài)自己為確定可達(dá)d(si,si)=1(1 ≤i≤n)，此類關(guān)系構(gòu)成的矩陣即是可達(dá)矩陣。

定義4：通過一個(gè)唯一標(biāo)識(shí)關(guān)聯(lián)區(qū)分不確定狀態(tài)轉(zhuǎn)移系統(tǒng)中任意不確定動(dòng)作，記為Tx。狀態(tài)si執(zhí)行Tx后可能到達(dá)的狀態(tài)集合Tx.mark={sm,sn,s0,…,sz}稱為不確定動(dòng)作Tx的信念狀態(tài)。Tx.num是不確定動(dòng)作Tx的信念狀態(tài)個(gè)數(shù)。

定義5：在一個(gè)不確定狀態(tài)轉(zhuǎn)移系統(tǒng)，用s-i→s-j表示將狀態(tài)si的可達(dá)信息s-i傳遞給狀態(tài)sj，d'(si,sj)表示經(jīng)信息傳遞后獲取的狀態(tài)si到狀態(tài)sj的可達(dá)關(guān)系。其信息傳遞原則如下：

若d(si,sk)=1，d(si,sj)=1||T||0 ，則s-i→s-j：d'(si,sj)=1；

若d(si,sk)=0 ，d(si,sj)=1||T||0 ，則s-i→s-j：d'(si,sj)=d(si,sj)；

若d(si,sk)=Tn，d(si,sj)=Tm，則s-i→s-j：d'(si,sj)=Tn+Tm；

若d(si,sk)=Tn，d(si,sj)=Tn，si-j[Tn].value=si-j[Tn].value+card(si-k[Tn].mark-(si-j[Tn].mark∩sk-j[Tn].mark))，當(dāng)si-j[Tn].value=Tn.value，則s-i→s-j：d'(si,sj)=1，否則為d′(si,sj)=Tn。

3 算法思想

3.1 狀態(tài)標(biāo)記

狀態(tài)標(biāo)記記錄著該狀態(tài)的最新狀態(tài)信息的更新是經(jīng)哪個(gè)狀態(tài)傳遞的，更新原則如下。

1）不確定系統(tǒng)的鄰接矩陣中所有狀態(tài)的初始標(biāo)簽tag均為0，若經(jīng)由傳遞后可達(dá)信息不變，tag 仍記為0。

2）狀態(tài)間的可達(dá)關(guān)系經(jīng)傳遞后形成確定可達(dá)關(guān)系或是由不可達(dá)成為不確定可達(dá)時(shí)，則更新為最新傳遞可達(dá)信息的狀態(tài)；

3）判斷可達(dá)關(guān)系是否不確定時(shí)，若根據(jù)原狀態(tài)si與sv的可達(dá)關(guān)系，狀態(tài)sv與狀態(tài)sx的可達(dá)關(guān)系，可得知狀態(tài)si到狀態(tài)sx的可達(dá)關(guān)系，此時(shí)記錄six.tag為最后一狀態(tài)編號(hào)加1。

當(dāng)系統(tǒng)中狀態(tài)si與sv的執(zhí)行動(dòng)作因其它因素發(fā)生變動(dòng)（包括邊的添加與刪除操作），則需重新判斷狀態(tài)si與狀態(tài)sv的可達(dá)關(guān)系，與原系統(tǒng)的可達(dá)矩陣中的對(duì)應(yīng)信息對(duì)比，若是不一致，則說明該狀態(tài)的可達(dá)信息變更了，因此經(jīng)該狀態(tài)sv作為中間狀態(tài)傳遞的可達(dá)信息也就會(huì)受到影響，需進(jìn)行更新；否則，無需更新。在此過程中，也會(huì)有狀態(tài)不受該執(zhí)行動(dòng)作變動(dòng)的影響，但仍需對(duì)其進(jìn)行轉(zhuǎn)發(fā)，直至受其影響的狀態(tài)均進(jìn)行比較、轉(zhuǎn)發(fā)操作或可達(dá)信息不再變更時(shí)，則該系統(tǒng)的狀態(tài)確定可達(dá)信息已求解出。

3.2 狀態(tài)可達(dá)關(guān)系更新

狀態(tài)之間可達(dá)關(guān)系更新步驟如下。

1）若狀態(tài)si與sv(i＜v)的可達(dá)關(guān)系變動(dòng)，則將可達(dá)矩陣R中滿足s-v.tag＞=i的狀態(tài)sv的可達(dá)信息恢復(fù)到變更后的鄰接矩陣B的狀態(tài)sv對(duì)應(yīng)可達(dá)信息，同時(shí)將狀態(tài)si（s-v.tag＜v）的可達(dá)信息再次傳遞到狀態(tài)sv。

2）若可達(dá)信息里原狀態(tài)可達(dá)矩陣D的狀態(tài)sv與當(dāng)前狀態(tài)sv不一致，則將sv中s-v.tag＜v的信息重新進(jìn)行傳遞，將需要更新的狀態(tài)（sx.tag＜v）的可達(dá)信息（需滿足s-x.tag＞=v）恢復(fù)為變更后的鄰接矩陣B的該狀態(tài)對(duì)應(yīng)的可達(dá)信息，再進(jìn)行傳遞，更新記錄可達(dá)信息變更的最后一狀態(tài)Colcmax，與其狀態(tài)可達(dá)標(biāo)記。

3）狀態(tài)sv的可達(dá)信息傳遞之后，再將下一狀態(tài)sv+1且sv+1.tag＜v+1的可達(dá)信息進(jìn)行傳遞，判斷哪些狀態(tài)的可達(dá)信息需要進(jìn)行更新，重復(fù)2）操作。

4）依次進(jìn)行轉(zhuǎn)發(fā)，直到最后更新的狀態(tài)的可達(dá)信息與原可達(dá)矩陣一致或者最后一個(gè)狀態(tài)的信息進(jìn)行轉(zhuǎn)發(fā)，則結(jié)束與原狀態(tài)可達(dá)矩陣的比較。

5）最后，再對(duì)可達(dá)矩陣進(jìn)行遍歷，找出所有元素值為0的點(diǎn)即為不確定可達(dá)矩陣。

證明：

可達(dá)狀態(tài)相關(guān)可達(dá)信息恢復(fù)到變更后的鄰接矩陣對(duì)應(yīng)信息，經(jīng)信息的傳遞，不會(huì)因?yàn)槿笔渌鼱顟B(tài)傳遞的信息而影響其最終的確定可達(dá)信息。因此，在信息傳遞之后，只需對(duì)找出所有不確定可達(dá)狀態(tài)對(duì)即可。

1）若狀態(tài)si與狀態(tài)sv之間是一型確定可達(dá)，可直接通過鄰接矩陣或經(jīng)信息傳遞可得。

2）若狀態(tài)si與狀態(tài)sv之間是二型確定可達(dá)，有此兩種情形：當(dāng)si-j[Tx].value=Tx.num，且狀態(tài)sv并非Tx的信念狀態(tài)時(shí)，根據(jù)中間狀態(tài)的可達(dá)信息，向確定可達(dá)狀態(tài)的傳遞信息原則，則必存在狀態(tài)sj(i≤j≤Colcmax) ，使得si-j[Tx].value=Tx.num，且si-j.tag＜=i，此si-j可達(dá)信息不會(huì)恢復(fù)變更后的鄰接矩陣對(duì)應(yīng)可達(dá)信息；當(dāng)sij的可達(dá)信息由原可達(dá)矩陣的確定可達(dá)恢復(fù)到不確定可達(dá)時(shí)，即狀態(tài)sv是Tx的信念狀態(tài)時(shí)，根據(jù)狀態(tài)向其確定可達(dá)的狀態(tài)進(jìn)行傳遞信息原則，則必存在狀態(tài)sj(i≤j≤Colcmax)，且si-j.tag＜=i，si-j[Tx].value=Tx.num-1，sv=si-v[Tx].mark-si-j[Tx].mark，經(jīng)信息的發(fā)送，使得si-v[Tx].value=Tx.num。

4 算法實(shí)現(xiàn)

設(shè)∑=(S,A,γ)為不確定狀態(tài)轉(zhuǎn)移系統(tǒng)，S為狀態(tài)集合，D為∑=(S,A,γ)的原狀態(tài)可達(dá)矩陣，B表示∑′=(S,A,γ′)狀態(tài)之間可達(dá)關(guān)系發(fā)生變更后的鄰接矩陣，R是∑′=(S,A,γ′)狀態(tài)可達(dá)信息更新后的狀態(tài)可達(dá)矩陣。算法如下：

根據(jù)原系統(tǒng)中的可達(dá)矩陣信息進(jìn)行更新，第2行是對(duì)狀態(tài)之間的執(zhí)行動(dòng)作發(fā)生變更的不確定系統(tǒng)∑'的鄰接矩陣的更新；第3～5 行是對(duì)受其影響的狀態(tài)所擁有的可達(dá)信息與原系統(tǒng)中的可達(dá)矩陣進(jìn)行對(duì)比并根據(jù)原則更新可達(dá)信息，否則直接進(jìn)行下一狀態(tài)的傳遞，且當(dāng)j=Colcmax時(shí)，結(jié)束更新；第6 行FINDCERTAIN（∑，R）函數(shù)是根據(jù)確定可達(dá)的狀態(tài)標(biāo)簽快速找出變動(dòng)后不確定系統(tǒng)∑',γ')其影響的狀態(tài)，并需將其狀態(tài)可達(dá)信息進(jìn)行傳遞，取得受其影響的其它狀態(tài)對(duì)之間的可達(dá)信息；第7 行是對(duì)不確定系統(tǒng)∑',γ')中狀態(tài)之間的不確定可達(dá)關(guān)系進(jìn)行修正。

函數(shù)FINDCERTAIN（∑，R）的具體實(shí)現(xiàn)過程如下：

第4行收集狀態(tài)si所擁有的可達(dá)信息。第5～7行尋找狀態(tài)si確定到達(dá)的狀態(tài)并將其可達(dá)信息傳遞給狀態(tài)sk，第8 行更新狀態(tài)變更的最大編號(hào)，確保受其影響的狀態(tài)都進(jìn)行了判斷。其中函數(shù)DELIVER（sk，s-i）的實(shí)現(xiàn)過程如下：

5 算法實(shí)例及仿真實(shí)驗(yàn)分析

如圖1，設(shè)∑=(S,A,γ) 為不確定狀態(tài)轉(zhuǎn)移系統(tǒng)。將通過文中描述的信息傳遞優(yōu)化算法對(duì)此轉(zhuǎn)移系統(tǒng)進(jìn)行維護(hù)。

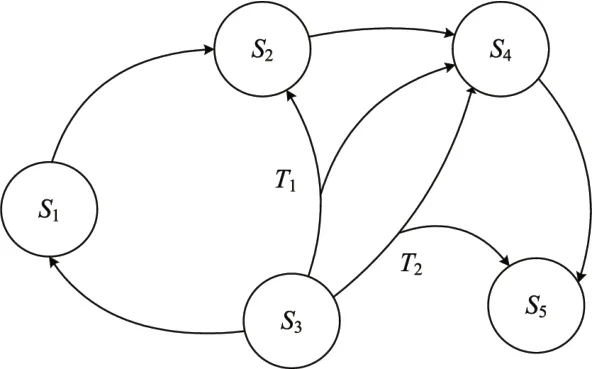
圖1 原不確定狀態(tài)轉(zhuǎn)移系統(tǒng)

參考文獻(xiàn)［15］的算法可得該不確定系統(tǒng)的狀態(tài)可達(dá)矩陣如下：

若因?yàn)橐恍┰蚴蛊洳淮_定系統(tǒng)的狀態(tài)s1與s2由確定可達(dá)變成不確定可達(dá)T3，與其它不確定動(dòng)作進(jìn)行區(qū)分，此時(shí)的不確定狀態(tài)轉(zhuǎn)移系統(tǒng)如圖2所示。

圖2 可達(dá)關(guān)系改變后的不確定系統(tǒng)

其鄰接矩陣變更為

因狀態(tài)s1到狀態(tài)s2與s3的可達(dá)信息都發(fā)生了變動(dòng)，所以需將原可達(dá)矩陣D中可達(dá)狀態(tài)s2與s3中分別滿足s-2.tag＞=1 與s-3.tag＞=1 的可達(dá)信息恢復(fù)到變更后的鄰接矩陣B的狀態(tài)s2與s3的對(duì)應(yīng)可達(dá)信息，此時(shí)Colcmax=3，可得：

重新將狀態(tài)s1的可達(dá)信息進(jìn)行信息傳遞，根據(jù)R[1][j].tag＜1 且R[1][j]=1 的條件，可知狀態(tài)s1無法進(jìn)行轉(zhuǎn)發(fā)。

但R[i][2]≠D[i][2]且Colcmax=3，則狀態(tài)s2需重新進(jìn)行信息傳遞，根據(jù)R[2][j]=1 且R[2][j].tag＜2 條件，可知R[2][3]=1，將可達(dá)矩陣R中狀態(tài)s2的可達(dá)信息傳遞給狀態(tài)s4，先將可達(dá)狀態(tài)s4的滿足S-4.tag＞=2 的可達(dá)信息恢復(fù)到變更后的鄰接矩陣B的狀態(tài)s4的對(duì)應(yīng)可達(dá)信息，再將R[i][2].tag＜2 的狀態(tài)可達(dá)信息進(jìn)行轉(zhuǎn)發(fā)，根據(jù)傳遞規(guī)則，得：

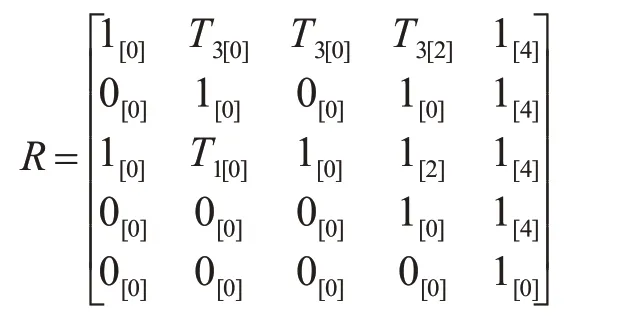
R[2][j]=1 再由狀態(tài)s3進(jìn)行信息傳遞，根據(jù)R[3][j]=1 且R[i][3].tag＜3 條件，可知R[3][1]=1 和R[3][4]=1，因此可達(dá)矩陣R中狀態(tài)s3將自己的可達(dá)信息傳遞給確定可達(dá)的狀態(tài)s1和狀態(tài)s4，此時(shí)Colcmax=4 根據(jù)信息傳遞規(guī)則可得：

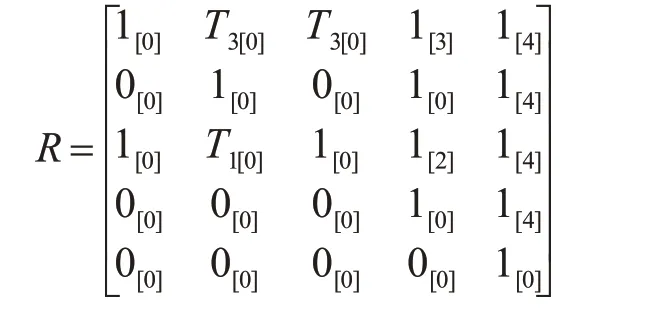
R[i][4]的可達(dá)信息D[i][4]的可達(dá)信息相等，且Colcmax=4，因此不需再更新。

這樣已找出了變更后的不確定系統(tǒng)中所有確定可達(dá)關(guān)系，最后對(duì)更新后的可達(dá)矩陣R中元素值為0 的狀態(tài)可達(dá)關(guān)系進(jìn)行判斷，最終得到的可達(dá)矩陣為

仿真實(shí)驗(yàn)對(duì)比如下。

以下為采用本文改進(jìn)的信息傳遞方法維護(hù)狀態(tài)可達(dá)關(guān)系與采用信息傳遞法、矩陣相乘法重新進(jìn)行更新系統(tǒng)的狀態(tài)可達(dá)關(guān)系的實(shí)驗(yàn)結(jié)果比較，三個(gè)算法的輸入數(shù)據(jù)均相同，運(yùn)算時(shí)間如表1所示。

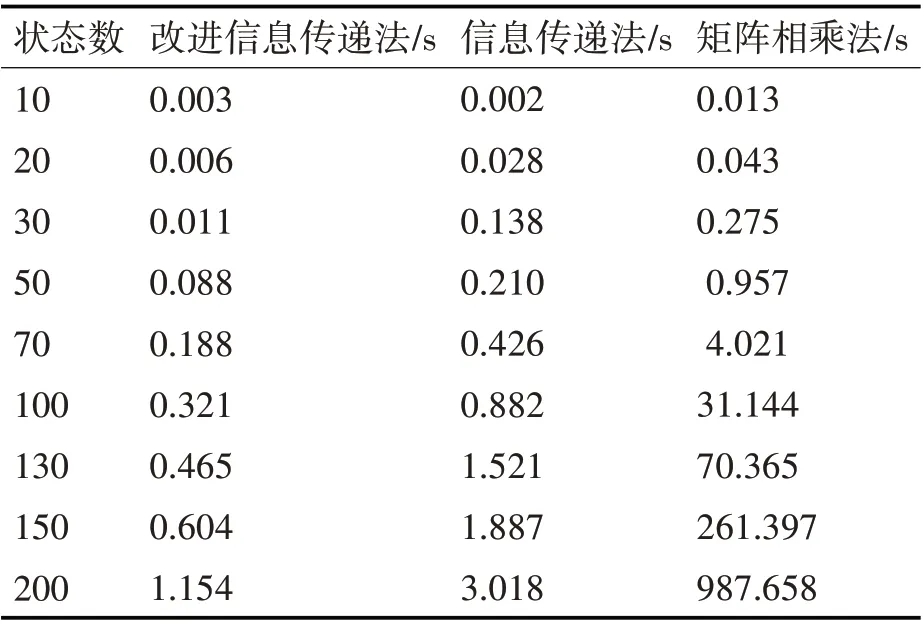
表1 運(yùn)行時(shí)間對(duì)比

當(dāng)狀態(tài)數(shù)較少時(shí)，系統(tǒng)中的動(dòng)作也會(huì)比較少，狀態(tài)之間的可達(dá)路徑會(huì)屈指可數(shù)。當(dāng)系統(tǒng)中的單個(gè)動(dòng)作執(zhí)行發(fā)生變動(dòng)時(shí)，可能會(huì)牽引到整個(gè)系統(tǒng)的狀態(tài)之間的可達(dá)關(guān)系的變動(dòng)。因此，此時(shí)系統(tǒng)中可達(dá)關(guān)系的局部維護(hù)與重新求解系統(tǒng)中可達(dá)關(guān)系的運(yùn)行的時(shí)間相差不大。

當(dāng)系統(tǒng)中狀態(tài)數(shù)逐漸增加時(shí)，其系統(tǒng)之中的動(dòng)作也隨之增加。由于狀態(tài)之間的可達(dá)關(guān)系可以通過其它動(dòng)作的執(zhí)行與其它狀態(tài)間接取得聯(lián)系，從而一個(gè)執(zhí)行動(dòng)作的變動(dòng)一般也不會(huì)影響整個(gè)系統(tǒng)中的狀態(tài)可達(dá)關(guān)系。因此，該動(dòng)作的變動(dòng)影響的大多數(shù)是系統(tǒng)中的局部狀態(tài)之間的可達(dá)關(guān)系，從而它的求解運(yùn)算量會(huì)比重新求解系統(tǒng)中的可達(dá)關(guān)系小很多，從而提高效率，且比文獻(xiàn)［15］所運(yùn)行的時(shí)間要少。

6 結(jié)語

本文從不確定系統(tǒng)中的信息傳遞方法切入，為加強(qiáng)算法的適用性，深入挖掘各個(gè)狀態(tài)維度的可達(dá)信息，快速求解系統(tǒng)的可達(dá)關(guān)系，維護(hù)不確定系統(tǒng)的相對(duì)穩(wěn)定性。今后的進(jìn)一步工作有：

1）完善系統(tǒng)傳遞方法，進(jìn)一步提高求解效率。

2）將傳遞法的思想應(yīng)用到多Agent 系統(tǒng)，或求解不確定規(guī)劃的規(guī)劃解中。