基于深度神經(jīng)網(wǎng)絡(luò)(DNN)的壓電陶瓷前饋補(bǔ)償研究

熊永程,賈文紅,張麗敏,鄭麗芳

(1.中國(guó)科學(xué)院 上海應(yīng)用物理研究所,上海 201800;2.中國(guó)科學(xué)院大學(xué),北京 100049;3.中國(guó)科學(xué)院 上海高等研究院,上海 201210)

0 引言

在同步輻射裝置中，從儲(chǔ)存環(huán)引出的同步光經(jīng)單色器真空腔內(nèi)兩塊晶體衍射后成為用戶實(shí)驗(yàn)單色光。單色器第二晶體俯仰角是調(diào)節(jié)兩塊晶體保持平行、獲得優(yōu)質(zhì)光斑的關(guān)鍵部件，要求其運(yùn)動(dòng)機(jī)構(gòu)具有響應(yīng)快，精度高及噪聲小等特點(diǎn)，同時(shí)由于單色器內(nèi)部空間狹小，故而其必須體積小，運(yùn)動(dòng)靈活，為此常應(yīng)用壓電陶瓷驅(qū)動(dòng)器來(lái)實(shí)現(xiàn)，運(yùn)動(dòng)精度為微米量級(jí)。為了獲得實(shí)驗(yàn)要求的優(yōu)質(zhì)同步光斑，在光束線調(diào)束優(yōu)化過(guò)程中，線站人員根據(jù)電離室讀數(shù)和電荷耦合器件(CCD)探測(cè)出光斑形狀，不斷地調(diào)節(jié)俯仰角和其他運(yùn)動(dòng)機(jī)構(gòu)，整個(gè)過(guò)程需要大量時(shí)間[1]。

每年運(yùn)行近5 000 h的上海同步輻射光源具有海量的數(shù)據(jù)資源，數(shù)據(jù)的高可用性為人工智能技術(shù)在同步輻射領(lǐng)域的應(yīng)用帶來(lái)巨大機(jī)遇。近年來(lái),上海同步輻射光源開展了基于差分進(jìn)化算法的智能光束線的探索并取得初步成功[2]。然而在智能調(diào)束過(guò)程中，研究人員發(fā)現(xiàn)引入單色器第二晶體俯仰軸后，由于其運(yùn)動(dòng)重復(fù)性差，優(yōu)秀個(gè)體遺傳到下一代失效，導(dǎo)致智能算法不收斂。影響俯仰軸運(yùn)動(dòng)重復(fù)性的因素有壓電陶瓷固有的遲滯非線性、蠕變屬性等。在不考慮振動(dòng)引起的誤差下，遲滯引入的不確定性一般為15%～20%，蠕變誤差為1%～5%[3]。

壓電陶瓷遲滯非線性特性及補(bǔ)償技術(shù)一直是國(guó)內(nèi)外學(xué)者的研究熱點(diǎn)[4-6]。早期的經(jīng)典前饋控制技術(shù)是應(yīng)用數(shù)學(xué)方法建立遲滯回線的擬合模型，通過(guò)求解其逆模型，得到激勵(lì)電壓與實(shí)際輸出位移的關(guān)系[7-9]。由于遲滯回線非線性特性復(fù)雜，盡管學(xué)者們提出了如Preisach模型、Bouc-Wen模型、Maxwell模型、多項(xiàng)式模型等數(shù)學(xué)模型，但其對(duì)遲滯回線的描述均存在一定局限性，因而一直是未被廣泛認(rèn)可的通用模型。

神經(jīng)網(wǎng)絡(luò)可用于擬合任意非線性曲線[10]，且具有泛化能力，理論上用神經(jīng)網(wǎng)絡(luò)擬合遲滯曲線是可行的。本文將壓電陶瓷主遲滯回線和次遲滯回線作為深度學(xué)習(xí)的訓(xùn)練數(shù)據(jù)集，在PyTorch框架下經(jīng)100 000輪訓(xùn)練，將得到的深度神經(jīng)網(wǎng)絡(luò)遲滯模型應(yīng)用于壓電陶瓷驅(qū)動(dòng)器的前饋補(bǔ)償。測(cè)試結(jié)果表明，應(yīng)用前饋補(bǔ)償后，被控滑臺(tái)的運(yùn)動(dòng)位移精度從開環(huán)狀態(tài)下的約8.91 μm提高到近80 nm，系統(tǒng)響應(yīng)帶寬100 Hz，可以應(yīng)用到智能調(diào)束系統(tǒng)單色器俯仰角的前饋控制中。

1 壓電陶瓷遲滯回線

壓電陶瓷遲滯非線性主要表現(xiàn)在輸入電壓與輸出位移的對(duì)應(yīng)曲線上。電壓上升與電壓下降時(shí)的曲線不重合，影響這一特性的因素不僅與當(dāng)前的輸入電壓有關(guān)，還與輸入歷史和輸入信號(hào)頻率等有關(guān)[11]。

本實(shí)驗(yàn)采用Physik Instrumente(PI)公司的E-709.CRG壓電陶瓷控制器及P-621.1CD壓電陶瓷微位移臺(tái)，控制器中集成了信號(hào)放大器，位移臺(tái)內(nèi)集成了電容傳感器。控制器接收命令后，通過(guò)信號(hào)放大器將電壓發(fā)送給位移臺(tái)，并從電容傳感器回讀壓電陶瓷當(dāng)前位置，向上通過(guò)USB與計(jì)算機(jī)通信，如圖1所示。

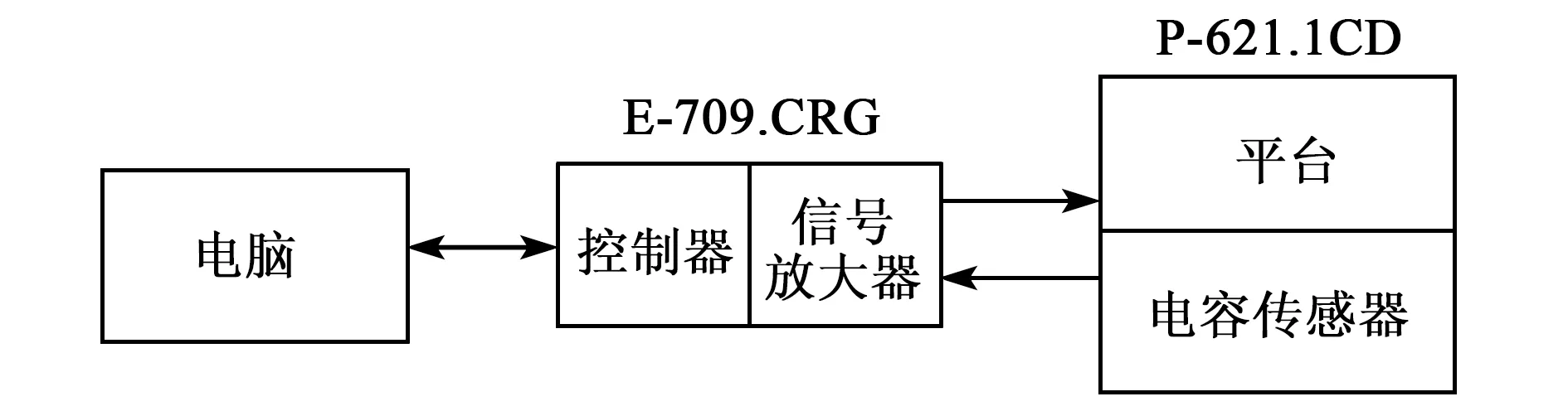
圖1 實(shí)驗(yàn)平臺(tái)通信圖

1.1 主遲滯環(huán)

輸入信號(hào)頻率為10 Hz，步長(zhǎng)0.1 V。升程曲線測(cè)試范圍為-5～107 V，回程曲線測(cè)試范圍為107～-6 V。以輸入電壓(V)為水平軸，輸出位移(x)為垂直軸，得到位移臺(tái)的主遲滯環(huán)。

對(duì)主遲滯環(huán)進(jìn)行線性擬合，得到x與V的線性關(guān)系為

x=0.976 579 417 023 688 6V+

0.274 239 524 880 049 05

(1)

圖2為升程曲線和回程曲線與擬合直線的偏差，升程曲線的最大偏差出現(xiàn)在107 V處，為-4.97 μm；回程曲線的最大偏差出現(xiàn)在40 V處，為8.91 μm。

圖2 主遲滯環(huán)線性分析結(jié)果圖

1.2 次遲滯環(huán)

當(dāng)輸入電壓為減幅正弦信號(hào)或增幅正弦信號(hào)時(shí)，壓電陶瓷的輸入電壓與輸出位移曲線呈現(xiàn)類似螺旋線的不相交遲滯環(huán)狀態(tài)，即次遲滯環(huán)。圖3、4分別為減、增幅正弦輸入信號(hào)時(shí)次遲滯線性分析結(jié)果圖。微位移臺(tái)對(duì)減、增幅正弦信號(hào)具有一定跟蹤能力，但是誤差比簡(jiǎn)單運(yùn)動(dòng)模式(步進(jìn)運(yùn)動(dòng))更大，對(duì)這兩種信號(hào)跟蹤的最大誤差均在6 μm左右。

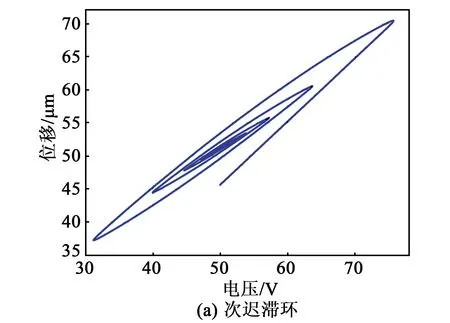
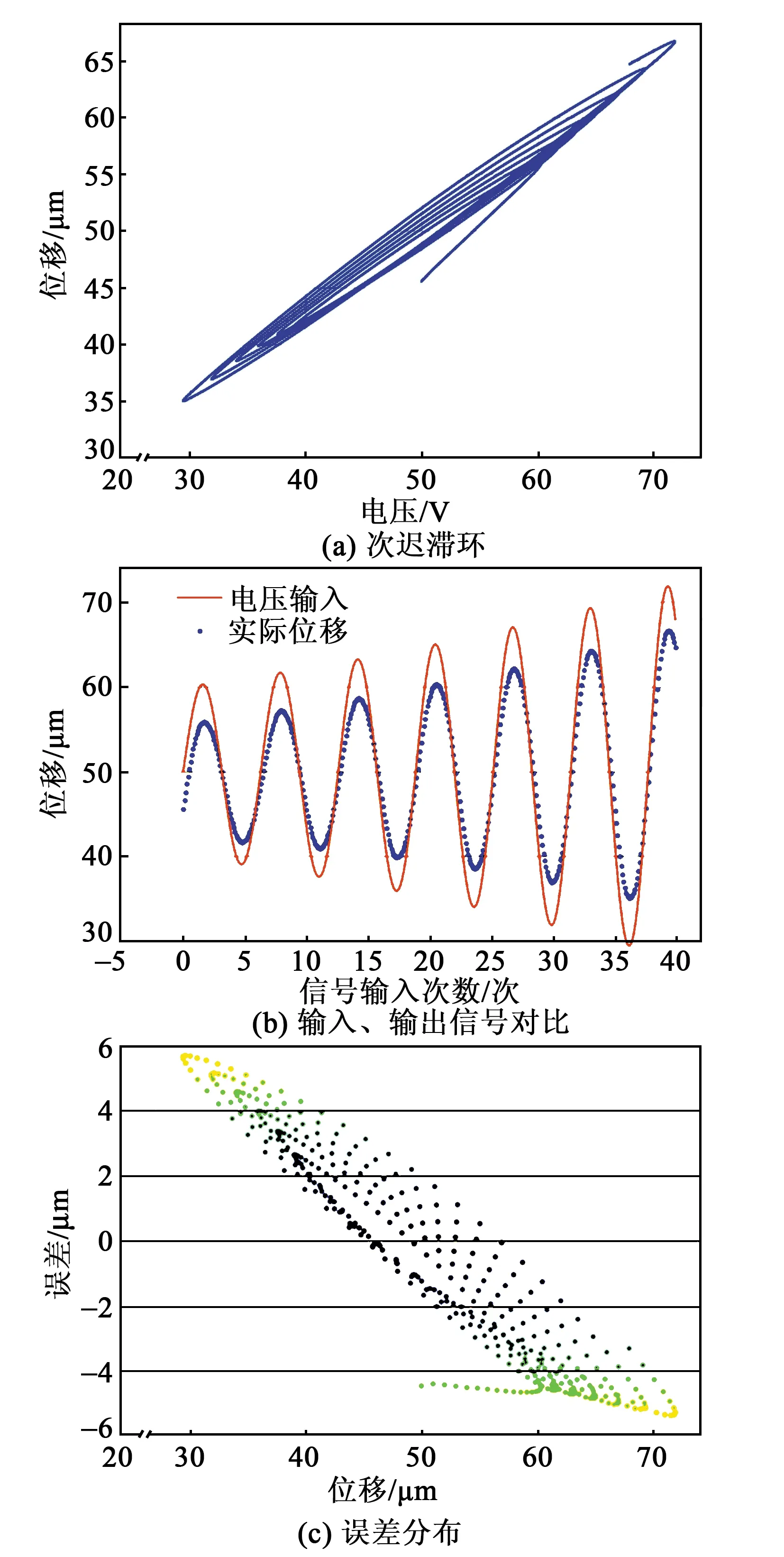
圖4 增幅正弦輸入信號(hào)的次遲滯環(huán)線性分析結(jié)果圖

從圖2～4可發(fā)現(xiàn)，滑臺(tái)當(dāng)前位置與當(dāng)前輸出電壓、上一次位移和上一次輸出電壓有關(guān)，即假定：

xt=f(Vt,xt-1,Vt-1)

(2)

式中：xt為當(dāng)前t時(shí)刻的位移；Vt為當(dāng)前t時(shí)刻的輸入電壓;Vt-1為上一位移的輸入電壓;xt-1為上一位移。

經(jīng)變換后可得：

Vt=f′(xt,xt-1,Vt-1)

(3)

將參數(shù)修改后可得：

VR=f′(xT,xt-1,Vt-1)

(4)

式中：VR為所需輸入的電壓；xT為給定的目標(biāo)位移；f′為由神經(jīng)網(wǎng)絡(luò)需要構(gòu)建的函數(shù)關(guān)系。

對(duì)于壓電陶瓷位移臺(tái)，由給定目標(biāo)位置、上一位置輸入電壓、上一位置位移，通過(guò)函數(shù)f′計(jì)算得到施加到壓電陶瓷的電壓值。

本文設(shè)計(jì)了一個(gè)基于深度神經(jīng)網(wǎng)絡(luò)的前饋控制模型，對(duì)預(yù)先設(shè)定的目標(biāo)位置進(jìn)行補(bǔ)償計(jì)算，將結(jié)果經(jīng)控制器輸出并施加給壓電陶瓷，實(shí)現(xiàn)微位移臺(tái)運(yùn)動(dòng)至目標(biāo)位置，圖5為整個(gè)系統(tǒng)的原理結(jié)構(gòu)圖。

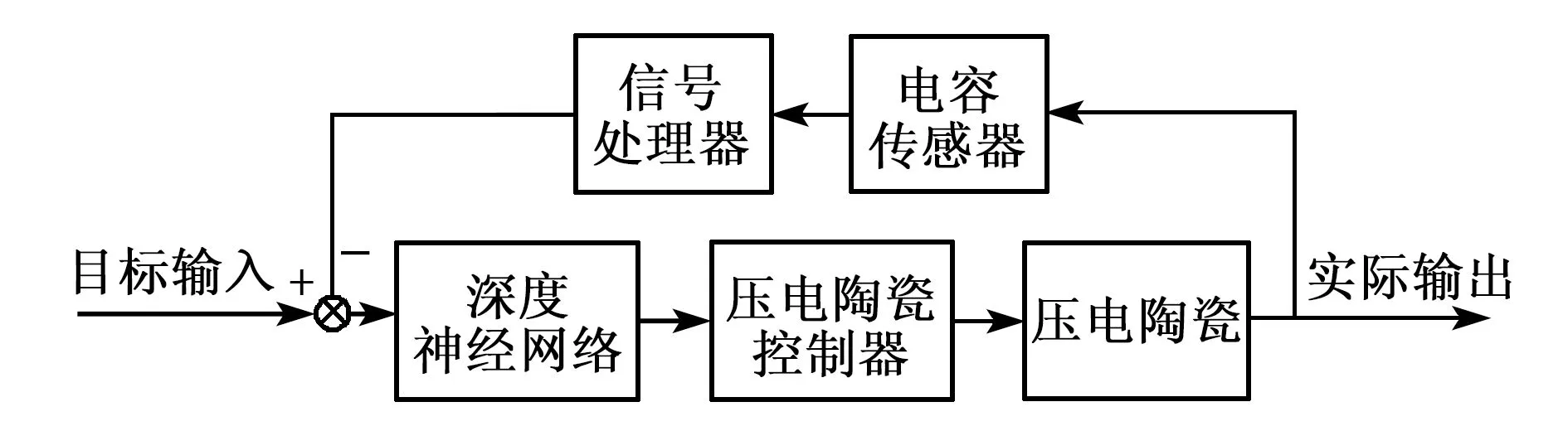
圖5 深度神經(jīng)網(wǎng)絡(luò)前饋控制示意圖

2 深度神經(jīng)網(wǎng)絡(luò)

一個(gè)或若干個(gè)神經(jīng)元組成一層神經(jīng)網(wǎng)絡(luò)，將若干層神經(jīng)網(wǎng)絡(luò)依次連接，得到一個(gè)深度神經(jīng)網(wǎng)絡(luò)(DNN)[12-13]，如圖6所示。

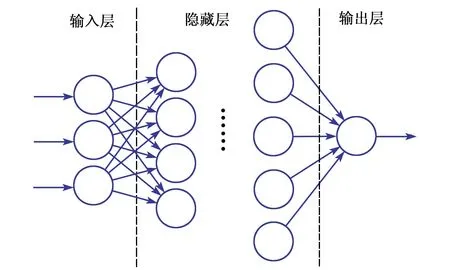
圖6 深度神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)

深度神經(jīng)網(wǎng)絡(luò)層與層之間是全連接的，即第i層的任意一個(gè)神經(jīng)元與第i+1層的任意一個(gè)神經(jīng)元相連，其計(jì)算關(guān)系如圖7所示。一個(gè)線性關(guān)系z(mì)=

∑(wixi)+b加上一個(gè)激活函數(shù)σ(z)，激活函數(shù)能夠增加神經(jīng)網(wǎng)絡(luò)的非線性表達(dá)能力，也對(duì)應(yīng)了壓電陶瓷的遲滯非線性。

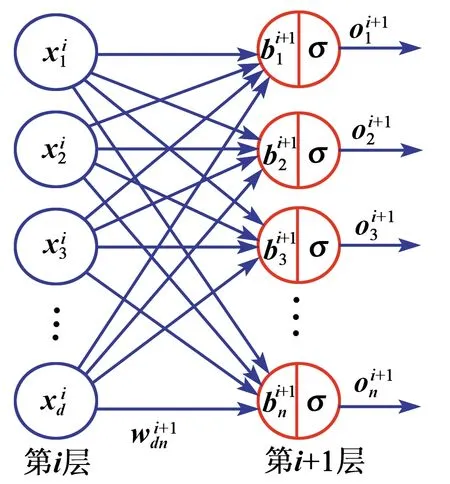
圖7 深度神經(jīng)網(wǎng)絡(luò)計(jì)算關(guān)系

假設(shè)第i層具有n個(gè)神經(jīng)元，第i+1層具有d個(gè)神經(jīng)元，第i+1層中每個(gè)神經(jīng)元包含一個(gè)偏置量，從第i層到第i+1層的關(guān)系為

(5)

將式(5)簡(jiǎn)化可得：

(6)

式中o為O矩陣中的元素。可將式(6)寫成矩陣形式：

O=σ(WX+b)

(7)

式中：O∈d×1為第i+1層的輸出，為空間，d×1為維度；W∈d×n為第i層到i+1層的隱藏層權(quán)重；X∈n×1為第i層的輸出；b∈d×1為第i+1層的偏置。

為了構(gòu)建更通用的多層網(wǎng)絡(luò)結(jié)構(gòu)，可以繼續(xù)堆疊這樣的隱藏層，如O(1)=σ1(W(1)X+b(1))和O(2)=σ2(W(2)O(1)+b(2))，一層疊一層，從而產(chǎn)生更有表達(dá)能力的模型[14]。

深度神經(jīng)網(wǎng)絡(luò)不僅有強(qiáng)大的非線性擬合能力、特征提取能力和容錯(cuò)能力，而且在面對(duì)海量、高維度的數(shù)據(jù)時(shí)，表現(xiàn)優(yōu)于機(jī)器學(xué)習(xí)[10]。

2.1 模型設(shè)計(jì)

設(shè)計(jì)的深度神經(jīng)網(wǎng)絡(luò)層數(shù)為9層，輸入層包含3維(當(dāng)前實(shí)際位移、上一次輸入電壓和上一次位移)，輸出層1維(壓電陶瓷輸入電壓)。訓(xùn)練數(shù)據(jù)集由第1節(jié)得到的3種遲滯回線的數(shù)據(jù)拼接而成，共有5 860組數(shù)據(jù)。表1為全連接層神經(jīng)元個(gè)數(shù)。

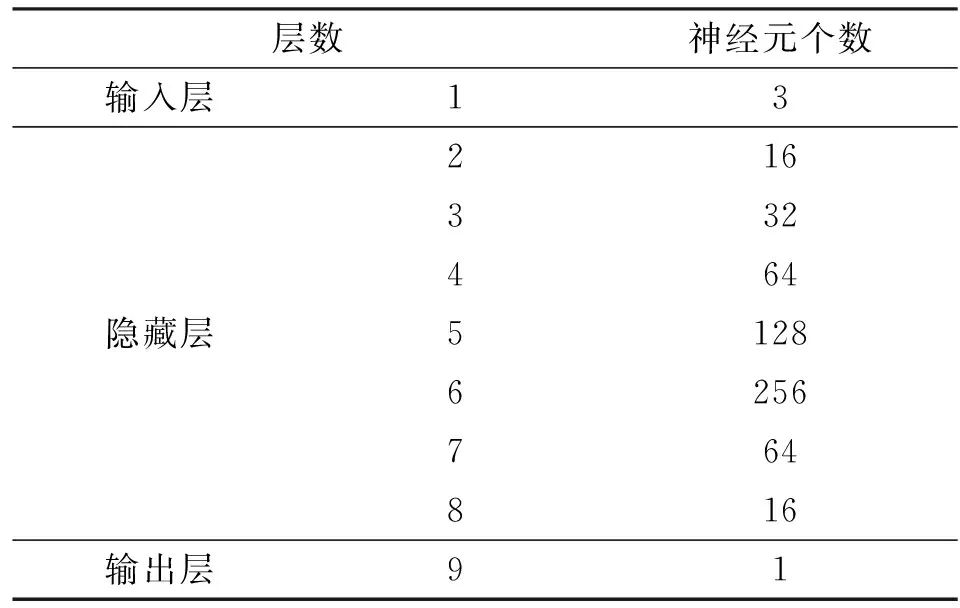
表1 全連接層神經(jīng)元個(gè)數(shù)

2.2 模型訓(xùn)練

2.2.1 訓(xùn)練過(guò)程

神經(jīng)網(wǎng)絡(luò)訓(xùn)練過(guò)程(見圖8)：

1) 初始化權(quán)重值參數(shù)，將每一組訓(xùn)練數(shù)據(jù)中的xt、Vt-1和xt-1作為神經(jīng)網(wǎng)絡(luò)的輸入，通過(guò)前向傳播算法逐層計(jì)算，得到輸入電壓預(yù)測(cè)值后，與Vt進(jìn)行對(duì)比，計(jì)算損失值。

2) 在反向傳播算法中，根據(jù)選擇的優(yōu)化器更新神經(jīng)網(wǎng)絡(luò)權(quán)重參數(shù)。經(jīng)過(guò)一輪一輪訓(xùn)練，得到最小損失值，此時(shí)神經(jīng)網(wǎng)絡(luò)模型為f′函數(shù)，見式(4)。經(jīng)過(guò)100 000輪訓(xùn)練后，得到了符合精度要求的模型，損失值如表2所示。

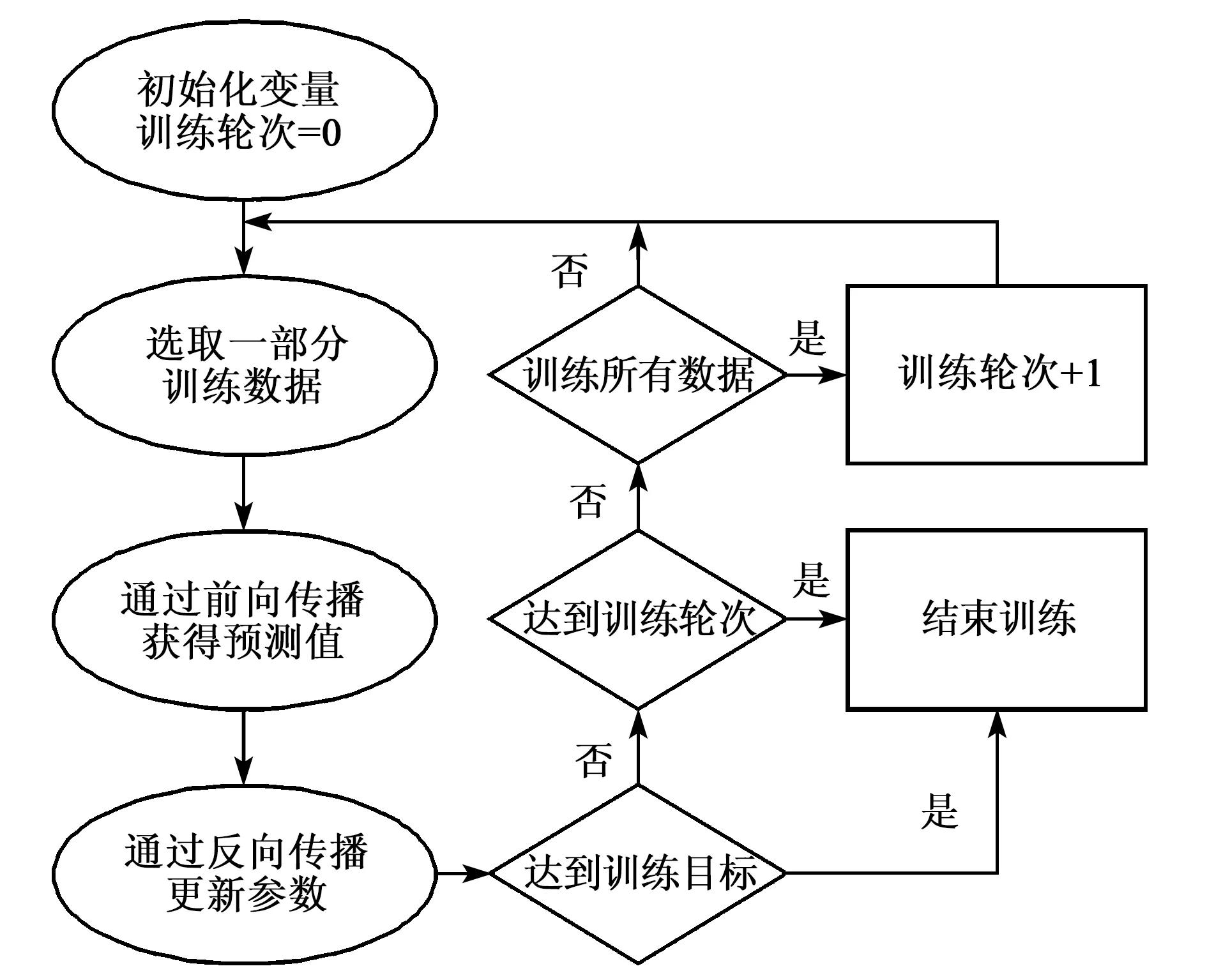
圖8 神經(jīng)網(wǎng)絡(luò)訓(xùn)練過(guò)程流程圖

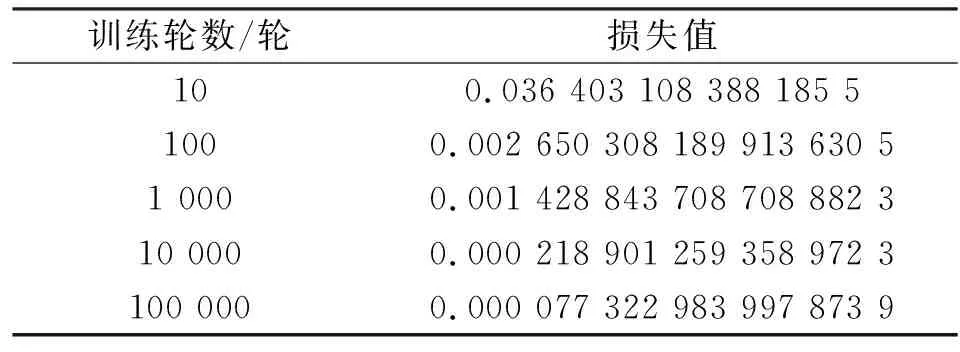
表2 損失值表

2.2.2 損失函數(shù)

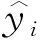
(8)

式中N為樣本大小。

2.2.3 優(yōu)化器與學(xué)習(xí)速率

在反向傳播算法中，選用目前最常用Adam優(yōu)化器作為參數(shù)更新方式，它能自適應(yīng)地調(diào)節(jié)學(xué)習(xí)速率αt，使訓(xùn)練能更快地收斂[15]。參數(shù)更新式為

(9)

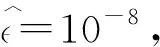
3 實(shí)驗(yàn)測(cè)試

在圖1實(shí)驗(yàn)平臺(tái)上對(duì)模型有效性進(jìn)行了驗(yàn)證。在PC端設(shè)置目標(biāo)位置分別以頻率為10 Hz的三角波、正弦信號(hào)、增幅正弦信號(hào)、減幅正弦信號(hào)變化，經(jīng)神經(jīng)網(wǎng)絡(luò)模型前饋補(bǔ)償后到控制器產(chǎn)生壓電陶瓷輸入電壓，測(cè)試微位移臺(tái)實(shí)際位置，結(jié)果如圖9～12所示。當(dāng)設(shè)置為三角波信號(hào)時(shí)，目標(biāo)位置與實(shí)際位置成良好線性關(guān)系，最大誤差值-0.088 μm，出現(xiàn)在初始點(diǎn)0處，穩(wěn)態(tài)誤差基本在±0.02 μm內(nèi)。當(dāng)目標(biāo)位置設(shè)置為正弦信號(hào)、減幅正弦信號(hào)和增幅正弦信號(hào)時(shí)，最大誤差都有不同程度的增加，分別為-0.67 μm，-0.66 μm和-0.27 μm，但仍出現(xiàn)在初始點(diǎn)處，系統(tǒng)穩(wěn)態(tài)誤差控制在±0.1 μm內(nèi)。由圖11、12可知，隨著振幅增大，誤差也相應(yīng)增大。

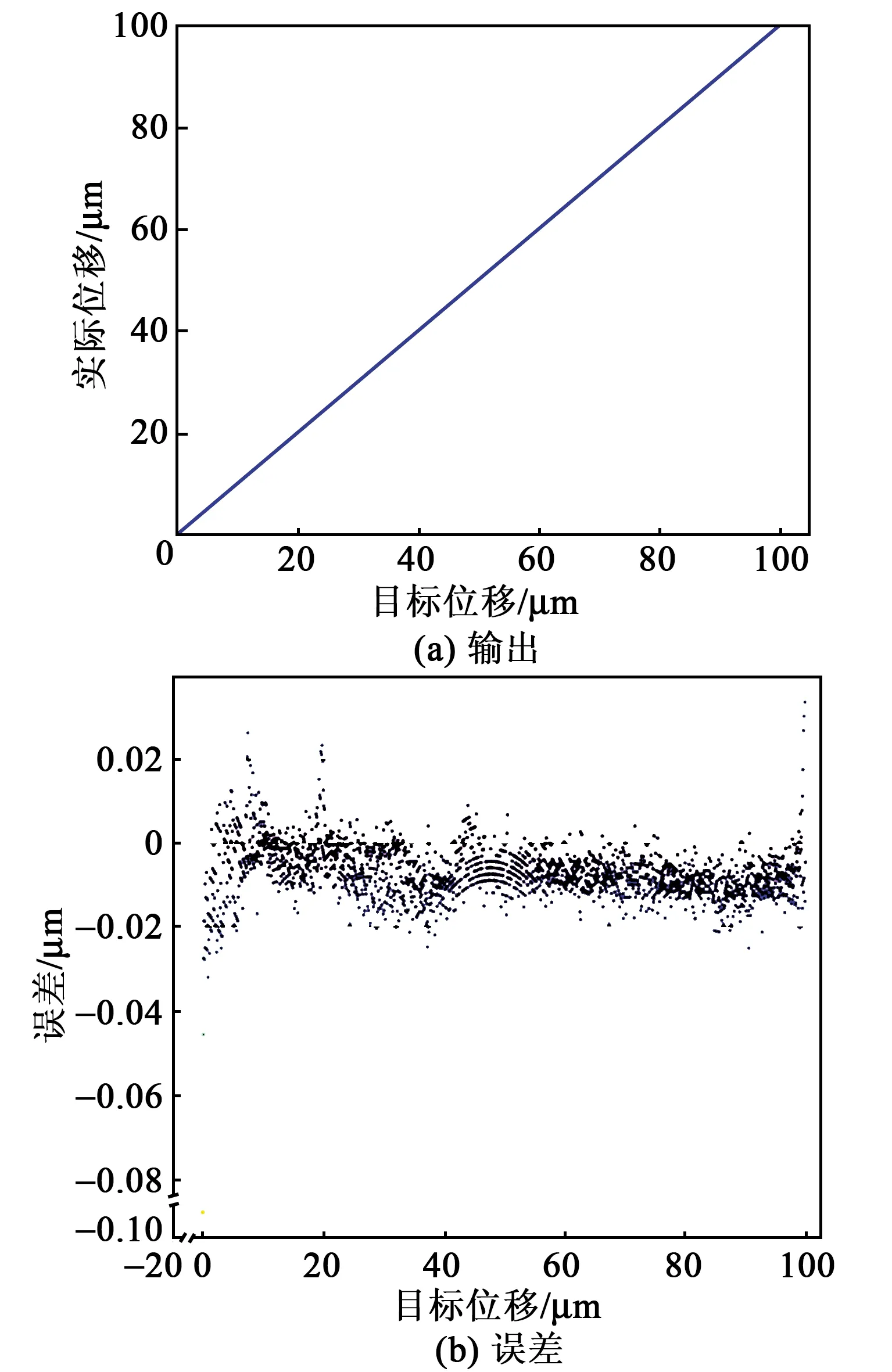
圖9 步進(jìn)運(yùn)動(dòng)控制效果圖

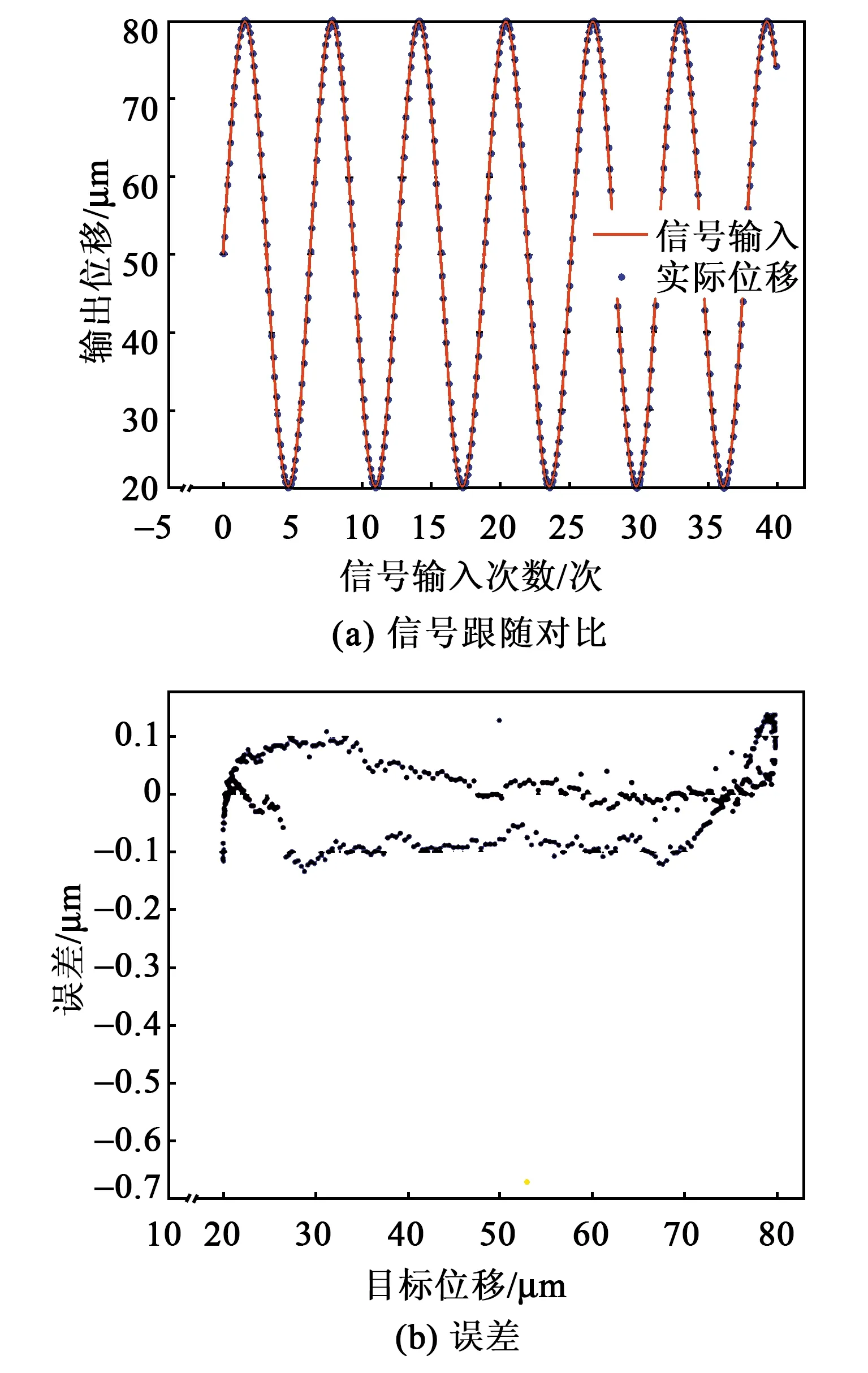
圖10 跟隨正弦輸入信號(hào)運(yùn)動(dòng)控制效果圖

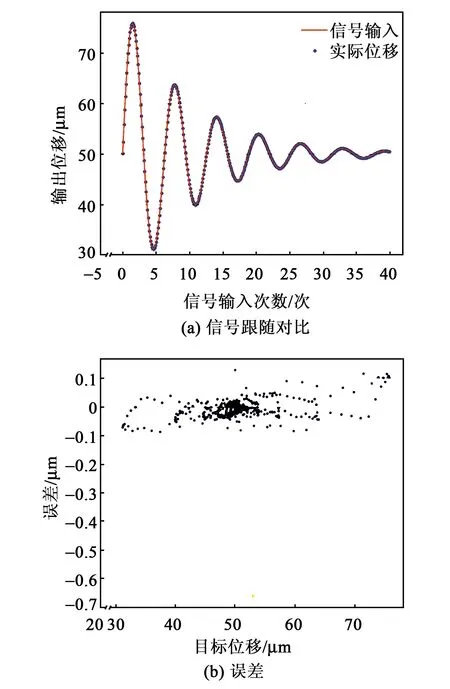
圖11 跟隨減幅正弦輸入信號(hào)運(yùn)動(dòng)控制效果圖

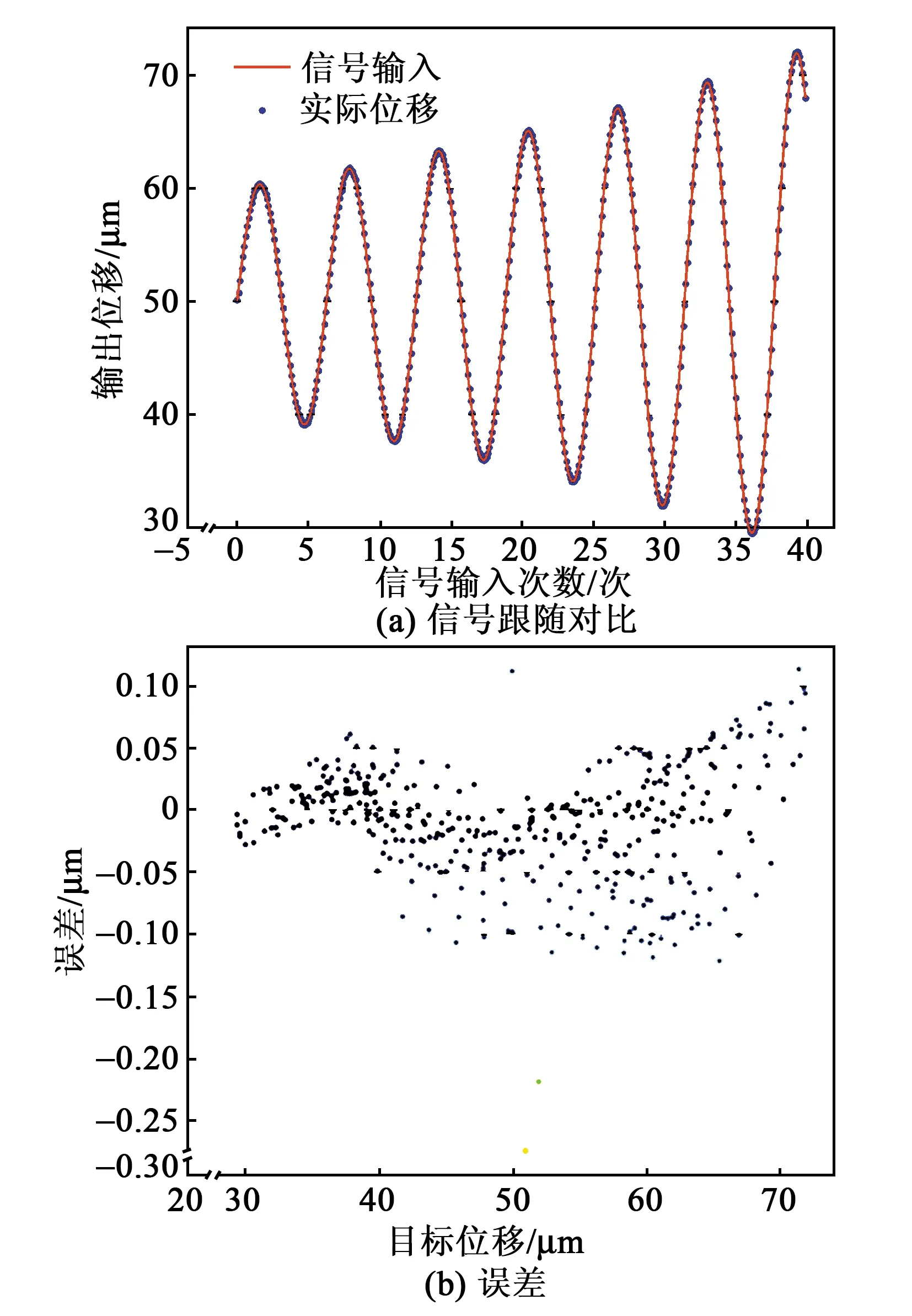
圖12 跟隨增幅正弦輸入信號(hào)運(yùn)動(dòng)控制效果圖

當(dāng)目標(biāo)位置依次按20 Hz、50 Hz和100 Hz三角波變化時(shí)，測(cè)試了微位移臺(tái)的實(shí)際位置，驗(yàn)證了神經(jīng)網(wǎng)絡(luò)模型的頻率泛化能力。

為了獲得較好的對(duì)比效果，應(yīng)用均方根誤差(ERMSE)反映誤差分布的離散程度，其表達(dá)式為

(10)

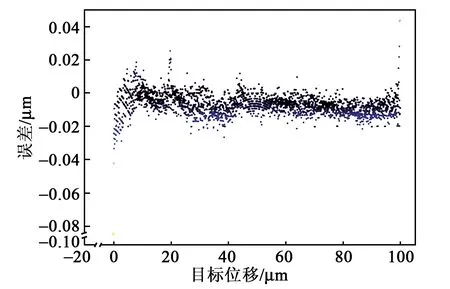
圖13 20 Hz輸入頻率控制效果圖

圖13～15分別為20 Hz、50 Hz和100 Hz時(shí)的控制效果圖。表3為不同輸入頻率下的控制效果對(duì)比。

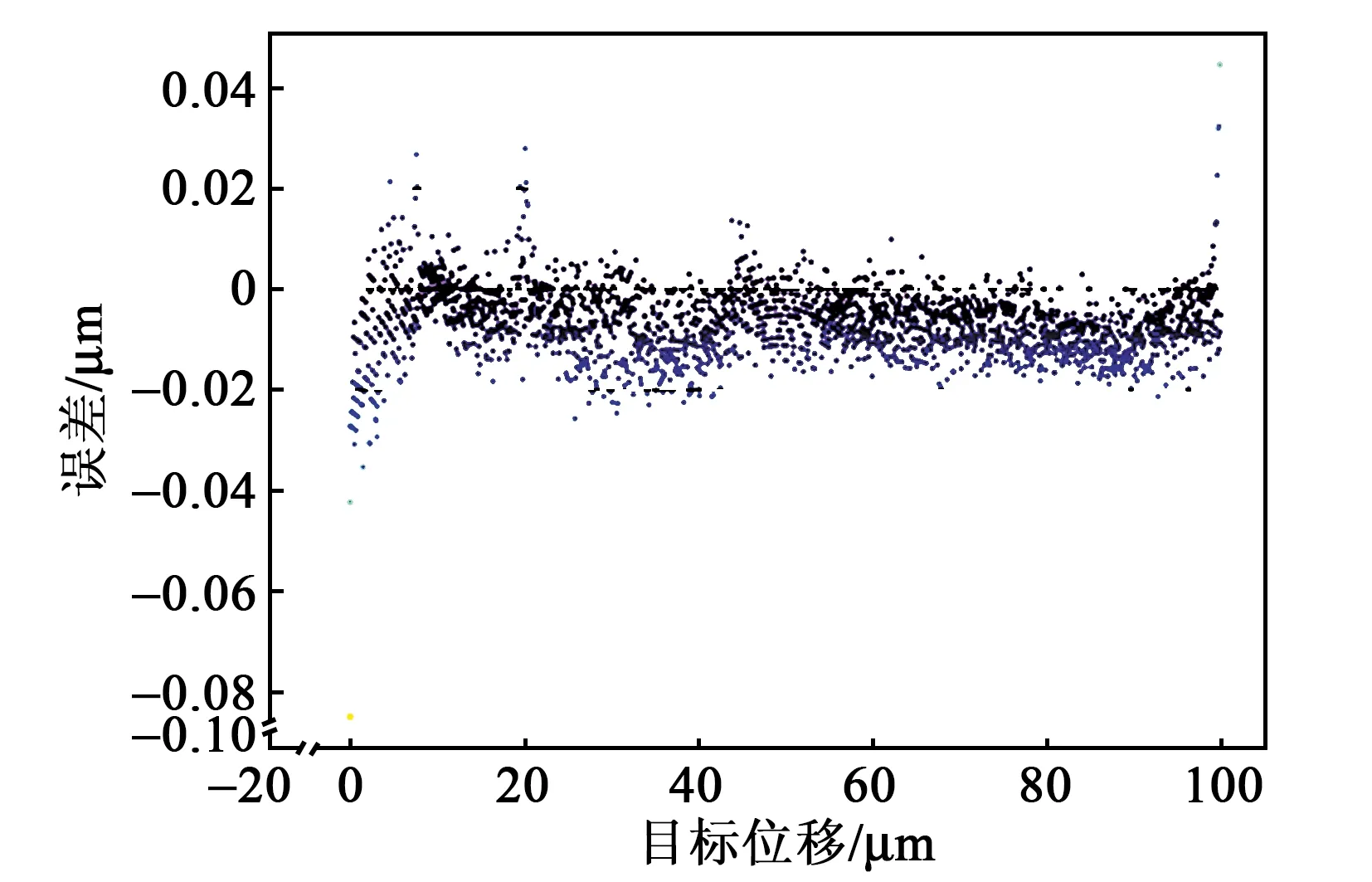
圖14 50 Hz輸入頻率控制效果圖

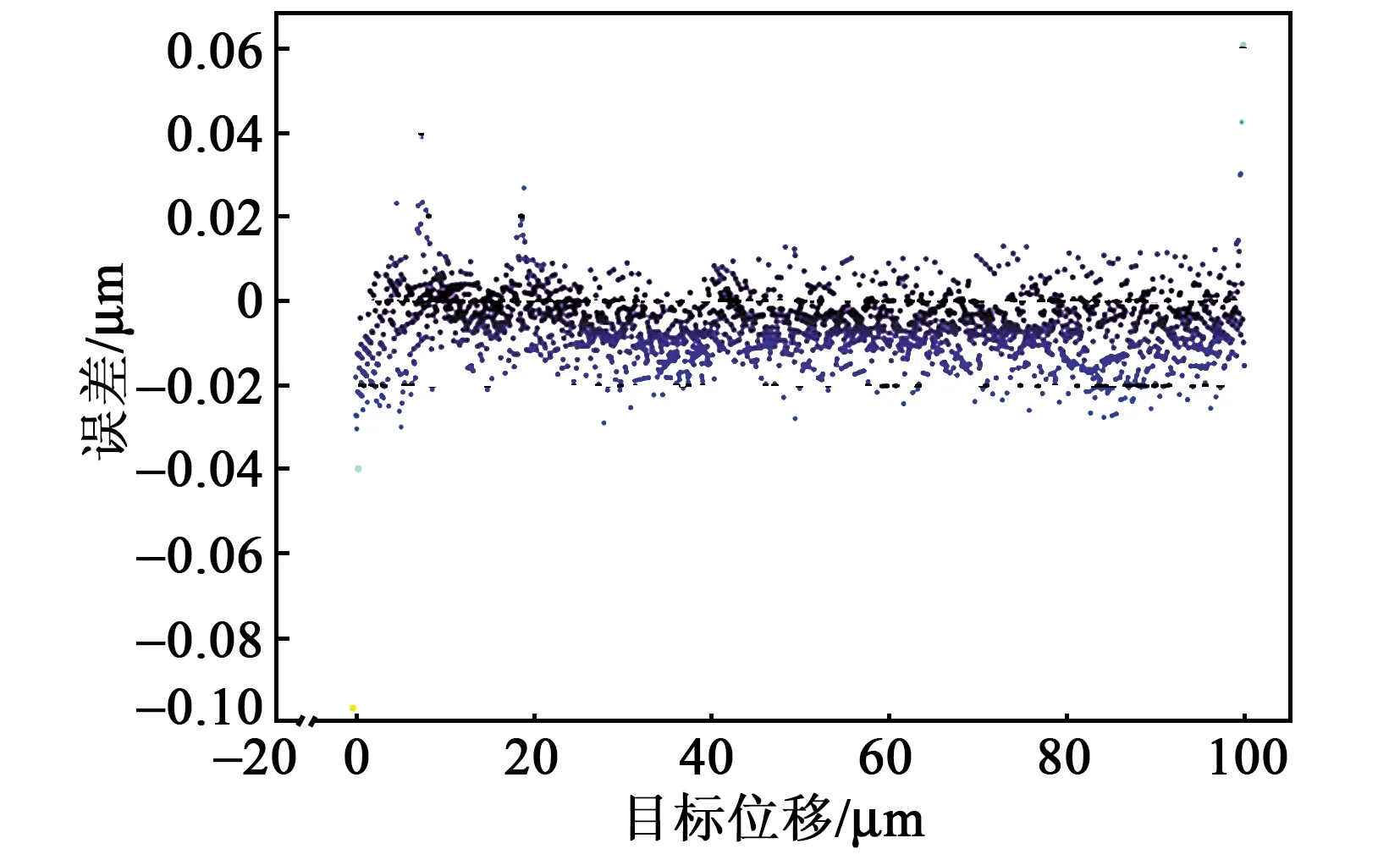
圖15 100 Hz輸入頻率控制效果圖

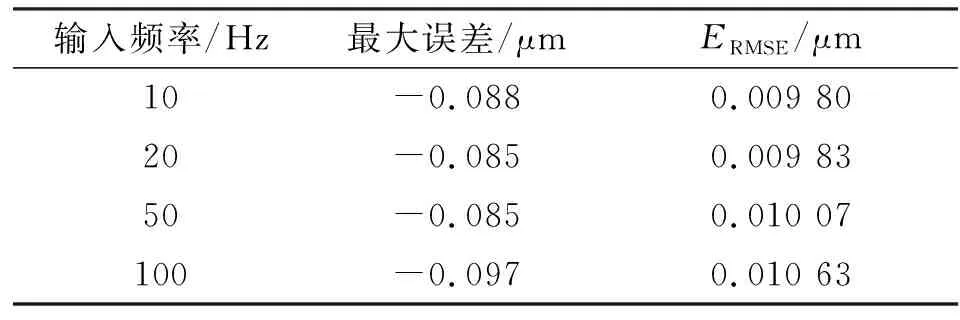
表3 不同輸入頻率下控制效果對(duì)比

由圖13～15可知 ，隨著目標(biāo)位置輸入頻率的升高，最大誤差和均方根誤差呈現(xiàn)增大的趨勢(shì)，說(shuō)明提高目標(biāo)位置輸入頻率會(huì)增加壓電陶瓷的遲滯非線性。當(dāng)輸入頻率為100 Hz時(shí)，最大誤差為-0.097 μm，仍在可接受的工程應(yīng)用范圍內(nèi)，表明構(gòu)建的深度神經(jīng)網(wǎng)絡(luò)模型在10～100 Hz具有良好的頻率泛化能力，整體上能以較高的精度擬合壓電陶瓷遲滯非線性特性。

4 結(jié)束語(yǔ)

本文基于PyTorch深度學(xué)習(xí)框架構(gòu)建了一個(gè)包含9層網(wǎng)絡(luò)結(jié)構(gòu)和ReLU激活函數(shù)的深度神經(jīng)網(wǎng)絡(luò)模型，給出了模型的設(shè)計(jì)原理和訓(xùn)練過(guò)程，并將訓(xùn)練得到的模型應(yīng)用于壓電陶瓷微位移臺(tái)的前饋補(bǔ)償。測(cè)試結(jié)果表明，在10 Hz的輸入信號(hào)下，位移最大誤差在-0.08 ～-0.67 μm，系統(tǒng)穩(wěn)態(tài)誤差為20～100 nm。隨著頻率的提高，誤差增加，100 Hz時(shí)最大誤差為-0.097 μm，仍在可接受的工程應(yīng)用范圍。結(jié)果說(shuō)明，本文構(gòu)建的深度神經(jīng)網(wǎng)絡(luò)能夠準(zhǔn)確地描述壓電陶瓷的動(dòng)態(tài)遲滯非線性，具有較好的頻率泛化能力，可以應(yīng)用在同步輻射光束線單色器第二晶體俯仰角前饋補(bǔ)償中，為優(yōu)化光束線實(shí)時(shí)智能調(diào)束系統(tǒng)提供參考和幫助。

本文應(yīng)用的深度神經(jīng)網(wǎng)絡(luò)模型的設(shè)計(jì)方法不僅適用于壓電陶瓷驅(qū)動(dòng)器前饋控制，對(duì)其他非線性系統(tǒng)建模也具有一定參考價(jià)值。用于深度神經(jīng)網(wǎng)絡(luò)建模的PyTorch框架，易于編程、參數(shù)調(diào)整和模型的實(shí)現(xiàn)只要對(duì)系統(tǒng)測(cè)量得到足夠多、覆蓋全的工作狀態(tài)作為構(gòu)建模型的訓(xùn)練數(shù)據(jù)集，然后構(gòu)建合理的神經(jīng)網(wǎng)絡(luò)，經(jīng)過(guò)足夠多的訓(xùn)練，最后就能得到與系統(tǒng)對(duì)應(yīng)的深度神經(jīng)網(wǎng)絡(luò)模型。