基于GA的卷積神經網絡結構化剪枝算法

賀天宇，田宗浩，張 航

(陸軍炮兵防空兵學院，合肥 230031)

1 引言

彈載圖像目標檢測系統利用采集的彈載圖像進行目標自主識別和定位，為跟蹤制導提供精確的定位信息。隨著深度學習(deep learning，DL)在目標檢測領域的推廣應用，卷積神經網絡 (convolution neural network，CNN)通過訓練學習得到圖像中的目標特征信息，檢測精度遠超過人工挖掘圖像特征目標檢測算法。而基于深度學習的目標檢測算法依賴于卷積神經網絡，在目標特征提取和推理過程中需要進行大量的計算，隨著網絡架構的深度不斷增加，模型的檢測精度不斷提高，隨之帶來的是龐大的數據量問題，尤其是訓練得到的參數信息會隨著網絡的深度成指數增加，這為在邊緣部署深度學習算法帶來了嚴峻挑戰。

對于嵌入式設備而言，存儲空間、計算資源、能耗以及體積限制了理論模型向工程實現的轉換，輕量化深度學習模型設計成為解決此問題的重要途徑。早在1989年深度學習模型還沒有被廣泛應用之前，Lecun教授就在文獻[4]中提出剔除神經網絡中不重要參數信息思想，達到壓縮模型尺寸的作用，當前很多深度學習模型剪枝算法都是基于文獻[4]中提出的OBD方法的改進。深度學習模型壓縮技術在于減少參數冗余而不會損失較大的預測精度，關鍵技術難點為壓縮量化指標的確定，其研究主要集中在精細化的模型設計、量化、Low-rank分解、模型/通道剪枝以及遷移學習等方面，相關研究均在特定模型中取得較好的壓縮效果，如圖1所示。

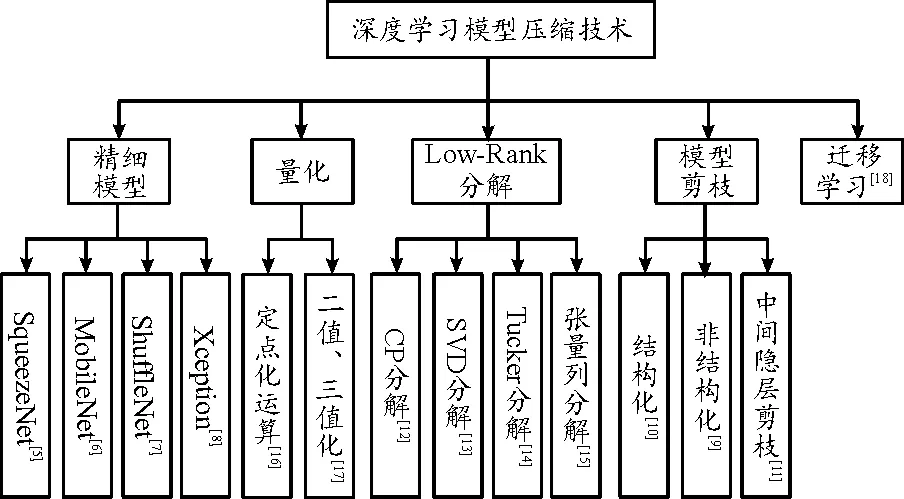
圖1 深度學習壓縮模型研究分類框圖

圖1中，深度學習模型精細化設計將卷積核分解成多個小卷積核組合，優化模型結構的同時大大減少網絡參數；量化是通過降低權重參數的比特位數進行模型壓縮，例如將32bit浮點權重轉換為8bit整型以及權重二值化、三值化等，在保證模型精度損失較小的情況下，極大地提高計算效率，降低內存占用率；模型訓練出的權重矩陣中很多信息是冗余的，Low-Rank分解是用若干小矩陣表達出大矩陣包含的信息，模型精度幾乎不變，而模型的計算復雜度和內存開銷大大降低；模型剪枝分為結構化、非結構化以及中間隱層剪枝，其核心思想是通過判定指標確定模型節點、通道以及參數的重要程度，剔除對模型精度影響不大的部分，并通過再訓練對模型進行微調。根據剪枝再訓練過程又可分為永久剪枝和動態剪枝，其中永久剪枝完全依賴于訓練模型的權重信息，裁剪完成后不再參與再訓練過程，但是對于網絡模型來說，某些權重信息是對后面權重參數的重要補充，永久裁剪后極大降低模型的精度，動態裁剪就是將這些誤裁剪的節點重新恢復回來，降低重要參數被裁剪的風險；遷移學習來源于Teacher-Student方法，在結構復雜、泛化性好、精度高的Teacher模型基礎上“引導”結構簡單、參數量少的Student模型訓練，得到和Teacher模型精度相近的結果。

因此，結合彈載平臺特殊的應用環境，在滿足目標檢測精度的前提下，設計高效的目標檢測算法，并且在不損失或損失較少目標檢測精度的情況下對網絡結構進行輕量化設計，降低模型訓練過程參數冗余和推理過程計算量，這對提高彈載圖像目標檢測精度和算法在彈載嵌入式平臺中部署有重要研究價值。

2 基于遺傳算法的模型壓縮方法

2.1 彈載平臺模型壓縮算法分析

圖1對當前的深度學習模型壓縮技術進行了概括分析，其中權重排序剪枝是眾多研究學者廣泛研究的模型壓縮算法，并取得一定的壓縮效果。但是權重排序剪枝算法類似于在參數空間中的一種暴力搜索，不同神經元的組合種類數以萬計，僅以權重值排序進行篩選只能在參數空間找到極少的一種組合方式，很多潛在的、壓縮率更高的組合并沒有搜索到。例如，以卷積層為例，所有卷積核是否去除用0或1表示，這些數字組成一個向量空間，該空間的維度與卷積層的卷積核數目一致，每一個數字在0和1之間變化時，都對應著該向量空間中的不同位置。基于權重的壓縮方法，只能兼顧到該高維空間中的極少幾個位置，對于廣闊的向量空間來說，該方法容易陷入局部最優。另外，權重排序剪枝算法基于“權重值偏小的神經元，對分類的意義很小”這一假設條件，在很多情況下權重偏小的神經元隨著訓練的迭代也會為分類提供較大的參考價值，對于此類神經元需要更深入的分析和觀察，而不是粗暴的過濾。

此外，網絡參數修剪也可以分為結構化和非結構剪枝，結構化剪枝為直接對卷積核的刪減，對網絡結構影響不大。而非結構剪枝為對卷積核內某一位置元素操作，會使網絡權重參數稀疏化。2種裁剪方式均可對模型達到很好的壓縮效果。但是非結構化裁剪會使模型在彈載嵌入式硬件平臺移植過程中造成無法高效使用密集乘法矩陣加速計算，硬件的計算成本和難度會大幅度提升。

因此，為提高在向量空間搜索時的覆蓋度以及對不同權重貢獻率的分析，降低后期算法向硬件平臺移植難度，找到更優的壓縮結果，本文采用遺傳算法(genetic algorithm，GA)對卷積核進行結構化剪枝，在全局搜索空間內對網絡參數進行壓縮，防止陷入局部最優，提高網絡壓縮后的整體效果。

2.2 遺傳算法

遺傳算法是模擬生物進化過程開發的搜索最優解計算模型，將求解最優解問題轉換成基因的交叉、變異和選擇算子過程，具有良好的全局尋優能力。GA以種群中的所有個體為對象，通過遺傳操作不斷地更新每個個體的基因序列，直到收斂到全局最優染色體序列，其流程如圖2所示。

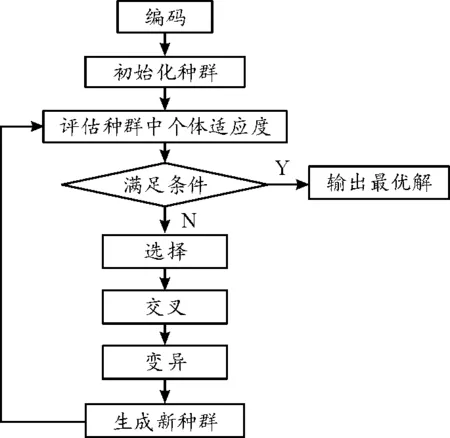
圖2 遺傳算法流程框圖

圖2為遺傳算法的基本流程，其中編碼方式、種群初始化、適應度函數以及遺傳操作中的選擇、交叉和變異是GA的關鍵步驟，文獻[20]中對GA實現流程進行了詳細介紹，本文不做贅述。

2.3 關鍵技術分析

卷積神經網絡一般由卷積層和全連接層組成，卷積層主要用來提取圖像中的特征信息，占據了整個網絡架構90%～95%的計算量和5%的參數量，而全連接層主要用來語義表達，判斷檢測目標的屬性，其占據了網絡5%～10%的計算量和95%的參數。為此，卷積層和全連接層的參數優化是模型壓縮的關鍵環節，結合圖2遺傳算法流程，對網絡中的卷積層和全連接層實現結構化剪枝，建立基于GA的模型壓縮算法。

1) 編碼

二進制編碼通過0和1來組成染色的基因序列，是GA染色體常用的編碼方式。為此，該算法用0和1作為卷積核的掩膜，以此標記卷積層中卷積核的保留和剔除，為壓縮過程中的卷積核表示提供了極大地便利，其編碼方式如圖3所示。

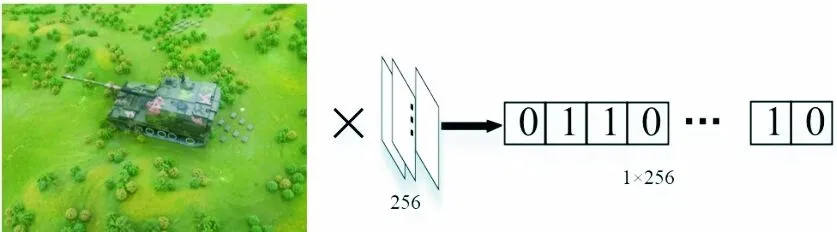
圖3 卷積核二進制編碼示意圖

圖3中，當卷積層總共包含256個卷積核時，則染色體的基因長度為256，全部都以0和1組成，每個數字與卷積核一一對應，作為該卷積核的掩膜，比如最左側數字對應最左側卷積核。

在完成GA迭代之后，得到了最優秀的染色體，根據最優染色體的DNA序列值來得到當前卷積層壓縮結果。例如，如果DNA某位置數字值是0，則將其對應位置的卷積核從網絡中刪除。如果是1，則保留該卷積核不動，將DNA解碼，便可得到模型結構化壓縮結果。

2) 適應度計算

適應度函數用來表征染色體基因序列遺傳給后代的概率，適應度高的染色體遺傳率高，相反則遺傳率低，故也稱目標函數。在目標檢測網絡中，每個染色對適應度的貢獻率用檢測精度表示，由分類結果和位置檢測精度兩部分組成。當分類結果錯誤時，貢獻率為0；當分類結果正確時，貢獻率為1。位置檢測精度貢獻率由真實框和檢測框的交疊程度表示，如圖4所示(IoU的計算方式)。

則，位置檢測精度貢獻率如式(1)所示：

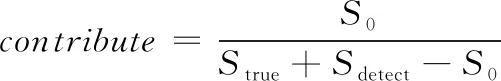
(1)

式中：為真實標注框；為檢測框；為交疊面積。利用位置和分類貢獻率，計算模型的mAP和網絡參數規模，并且確定單個染色體的適應度為：

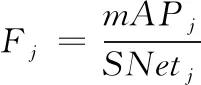
(2)

其中：和分別為第條染色體均值平均精度和網絡參數規模；為第條染色體的適應度。最終的適應度要同時兼顧兩個方面的性能，即“高檢測率，低網絡大小”。其網絡參數規模可以用式(3)表示：

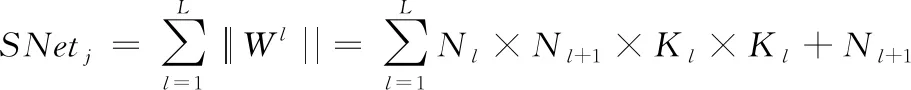
(3)

其中：為第卷積層的參數量；為第層卷積核大小；和+1分別為對應層通道數。由此可得壓縮比為：

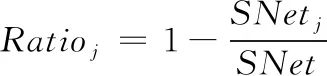
(4)

其中，為未壓縮參數量。

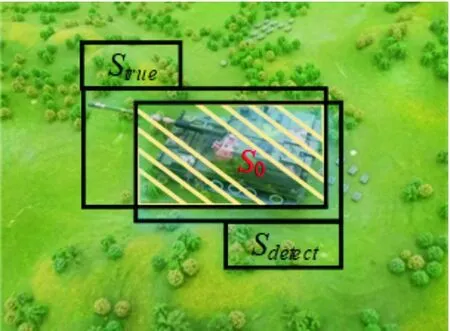
圖4 位置檢測精度貢獻率示意圖

另外，GA每一次迭代都需要計算每個染色體對應的適應度值，如果把所有樣本都用來計算適應度，則整個訓練過程的計算代價將非常大，嚴重影響遺傳算法的速度。為此，該算法將樣本集分成3個規模：小樣本集、中樣本集、大樣本集，在迭代過程中靈活使用不同規模的樣本集來彌補計算量太大的問題。

例如，如果檢測任務總共包括10類目標，每一類目標有10 000個樣本，總計100 000個樣本。其中，小樣本集包含10類目標，每一類隨機從總樣本中挑選出100個樣本；中樣本集包含10類目標，每一類也是隨機挑選1 000個樣本；大樣本集是總體樣本。雖然小樣本集得到的適應度相比于中樣本集、大樣本集有所偏差，但遺傳算法本身是一種“粗獷”的搜索方法，其更加注重在向量空間中進行大范圍的覆蓋，以防止過早進入局部最優。因此，小樣本集帶來的適應度偏差在接受范圍內，并且可以通過反復迭代和更新樣本集來提高其壓縮精度。

3) 遺傳操作

遺傳操作包含算子選擇、交叉和變異，各步驟方法和傳統方法類似。

2.4 模型建立

通過上述分析，基于遺傳算法的模型壓縮算法流程可以在圖2的基礎上更新為圖5。

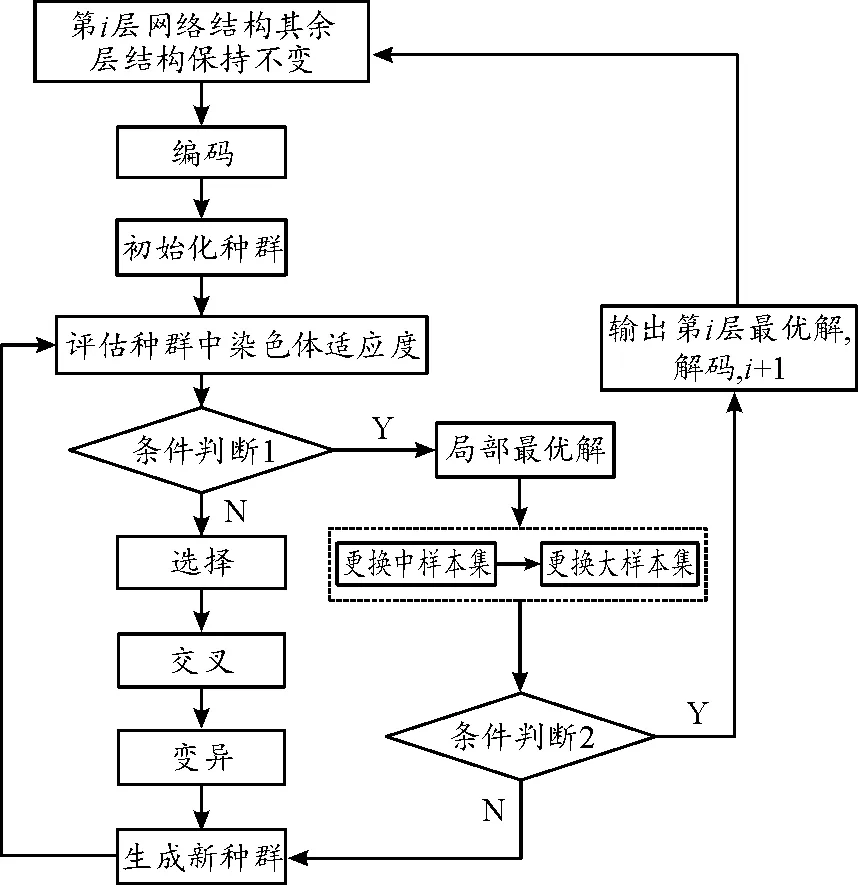
圖5 基于GA的模型壓縮流程框圖

由圖5可以分析基于GA的網絡壓縮過程為：

Step 1：選定壓縮網絡層

當前，基于深度學習的目標檢測網絡結構復雜，該算法從輸入層網絡開始，逐層進行壓縮。即，先用GA完成第一個卷積層中冗余卷積核的去除，此后再考慮第二個卷積層，在對第一個卷積層處理的過程中，后續所有的卷積層都保持不動。

Step 2：編碼及初始化

每個染色體對應的DNA基因序列由個數字組成(數字為0或1)，與當前卷積層的卷積核數量一致。DNA的每一個位置的數字值，根據隨機分配為0或1，其中0表示該卷積核會被刪除。設置染色體初始值Num和基因隨機編碼比例，即DNA中的0的數量比例。

Step 3：計算每個染色體的適應度值

利用式(2)計算每個染色體的適應度值，記錄適應度最好的染色體，將其作為歷史最優染色體。

Step 4：遺傳操作

Step 5：生成新種群，計算下一代染色體適應度

記錄當前適應度最好的個體，將其與歷史最優染色體進行比較，以此實現歷史最優染色體更新。

Step 6：循環上述步驟Step 3～Step 5一定的次數，直到當前樣本集上的適應度提升沒有明顯變化為止(條件判斷1)

Step 7：更換樣本集

更換樣本集，重復步驟Step 3～Step 6，當大樣本集遍歷完成后輸出最優解(條件判斷2)，即在大樣9本集上的適應度提升沒有明顯變化。為了降低樣本集變大帶來的速度影響，保留上一層級樣本集尋優結果中比例的最優染色體作為初始染色體。

Step 8：輸出最優解，解碼獲得最優壓縮結果

上述迭代完成后，解碼歷史最優染色體DNA序列，根據序列中的0、1掩膜決定其對應位置的卷積核是否從網絡中刪除，完成當前層網絡壓縮，重復Step 2～Step 7繼續下一層網絡壓縮。

3 試驗

為驗證本文壓縮算法的有效性，分別以LeNet-5和AlexNet卷積網絡為基準進行逐層壓縮，數據集分別為MNIST和CIFAR-10，對比分析各層壓縮后的參數變化。

LeNet-5卷積網絡是在LeNet基礎上改進的，網絡結構相對簡單，由標準卷積層和全連接層組成，其網絡結構圖如圖6。

其中，LeNet-5分別由3個卷積層、2個池化層和1個全連接層組成，其各層參數如圖6所示。

從表1中發現，因LeNet-5模型各層卷積核數量較少，LeNet-5模型的整體壓縮比為0.783 4。其中第1個卷積層C1無法進行壓縮，刪減任何一個卷積核，都會引起整個網絡性能的下降，主要歸因于第一個卷積層提取的特征是后續特征學習的基礎。卷積層C5和全連接層F6的單層壓縮率較高，驗證了卷積層和全連接層是模型結構化壓縮的重點。此外，原LeNet-5模型的檢測精度為99.2%，經過壓縮后模型的檢測精度為99.07%，模型壓縮后的檢測精度損失0.13%。

同理，對AlexNet卷積網絡在數據集CIFAR-10的訓練結果進行壓縮，其結果如表2所示。

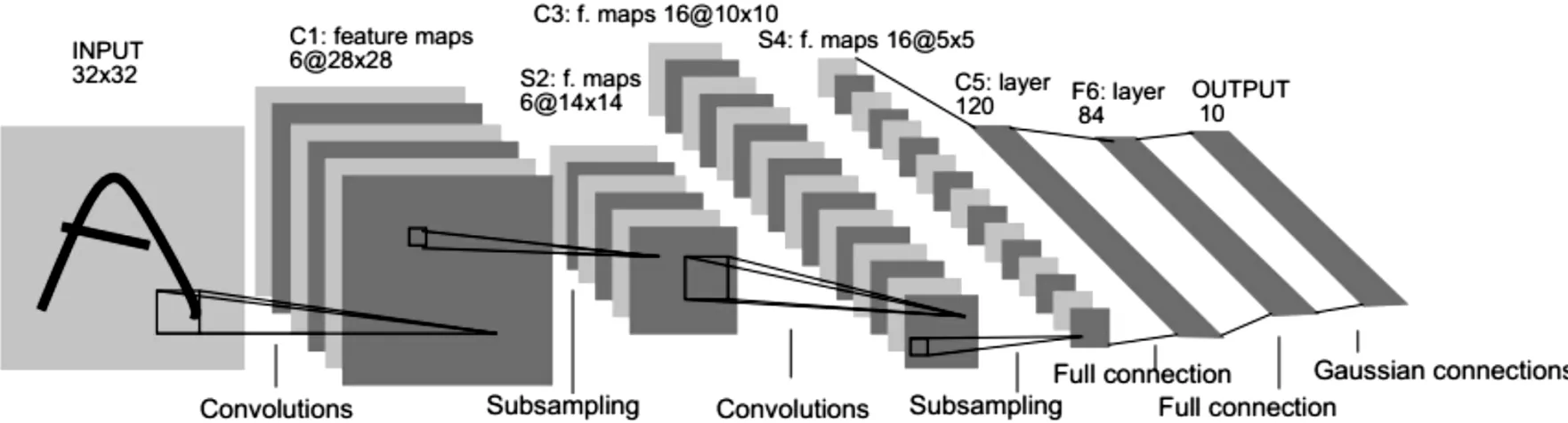
圖6 LeNet5網絡結構圖

表1 LeNet-5壓縮前后參數量對比(MNIST數據集)

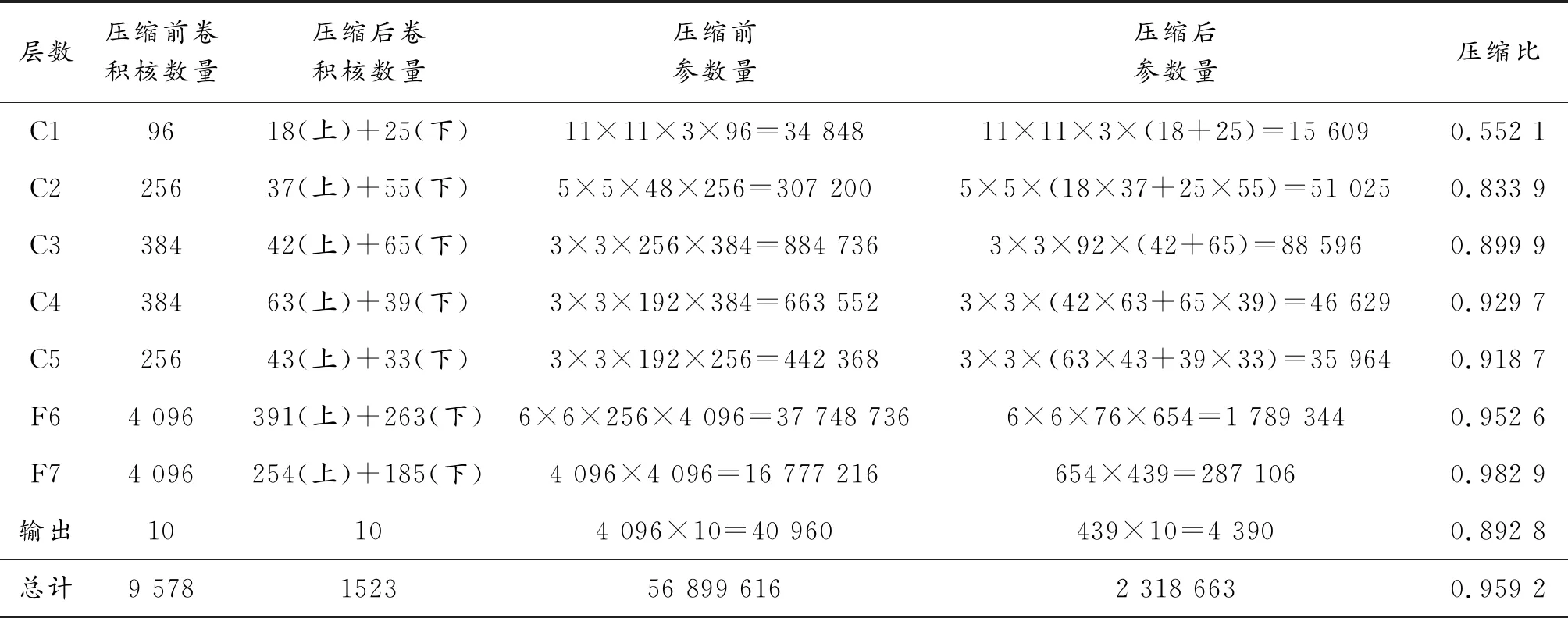
表2 AlexNet壓縮前后參數量對比(CIFAR-10數據集)

通過表2分析發現，本文算法能夠實現對AlexNet網絡參數95.92%的壓縮，大大降低模型的參數量。從各層壓縮比分析出，初始層卷積核壓縮比相對較低，隨著網絡深度的不斷遞增，模型冗余參數不斷增多，壓縮比不斷增高，體現了初始卷積層對特征學習的重要性。另外，未壓縮模型的檢測精度為81.32%，壓縮后模型的檢測精度為80.76%，模型精度損失0.56%。

另外，為進一步驗證本文模型的有效性，對比分析采用文獻[21]權重裁剪算法、L1范數結構化剪枝算法以及本文算法的壓縮性能參數，基準網絡選用上述AlexNet網絡，其結果如表3所示。

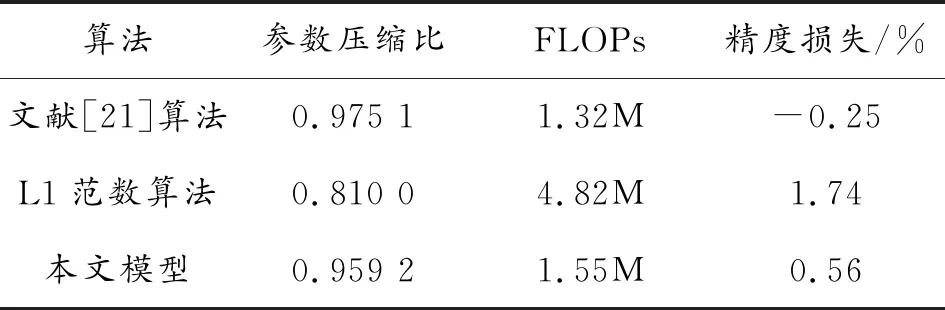
表3 不同算法模型剪枝性能分析結果

從其中可以看出，因文獻[21]提出的權重裁剪算法為細粒度剪枝，可以保留卷積核內的有用信息，而L1范數算法和本文算法為粗粒度剪枝，裁剪完后的卷積核內仍存在一定的權重冗余，但因本文模型是在全局范圍內對卷積核的重要性進行評估，大大提高了裁剪的準確率，達到較好的壓縮效果，并將精度損失控制在1%以內。另外，文獻[21]提出的算法會造成權重稀疏連接，對硬件平臺友好性差，而本文算法對于彈載異構硬件平臺的適應性較好，可以高效利用硬件乘加器實現矩陣的快速計算，降低算法向異構硬件平臺移植的難度。

4 結論

為降低深度學習算法向彈載嵌入式硬件平臺部署的難度，提出了基于GA的結構化模型壓縮算法，主要創新點為：

1) 利用遺傳算法在全局空間的搜索特性對模型各層卷積核進行結構化剪枝，解決傳統權重剪枝易陷入局部最優和剪枝結果對硬件平臺不友好問題；

2) 提出“高檢測率，低網絡大小”的模型壓縮判別指標，獲得精度損失低、模型壓縮率高的輕量化模型結構；

3) 優化樣本集規模，解決整個訓練過程計算代價大等問題，提高基于GA的模型壓縮算法執行速度。