基于加速魚群算法的鋰離子電池剩余壽命預測

何 星，丁有軍，宋麗君，殷春武

(1.西安建筑科技大學 信息與控制工程學院， 西安 710055; 2.國防科技大學 裝備綜合保障技術重點實驗室， 長沙 410073)

1 引言

鋰離子電池具有高能量密度、低自放電率、長壽命、無記憶效應以及寬溫度范圍等優點，已經成為新能源電動汽車、航空航天以及國防軍事等領域中非常重要的儲能裝置。國際信息咨詢公司IHS 預計，到2025年全球儲能裝置中鋰電池將會占據超過80%，我國已將高安全性、低成本、長壽命鋰電池列為《中國制造2025》與《能源技術革命創新行動計劃(2016—2030年)》規劃中的重點研究發展領域，將其視為解決交通能源危機與環境保護問題的良藥。與此同時，在循環使用過程中，因外部環境和內部電極材料腐蝕、隔膜老化等原因，會引起鋰離子電池性能逐漸退化和失效，可靠性、安全性和壽命已成為制約其成功應用的至關重要問題。近年來，鋰離子電池壽命預測和健康管理已成為預防鋰離子電池失效性事故，確保設備運行安全的關鍵技術。

在鋰離子電池剩余壽命預測方法中，基于模型的方法旨在通過分析鋰離子電池內部電化學反應的本質機理，建立描述其退化行為的數學模型，再外推實現電池剩余壽命預測。物理模型能夠獲得較高的預測精度，但涉及過多的參數使得精確建模十分困難。此外，固體電解質膜、電化學阻抗譜等電化學特性參數測量困難，也使得基于物理模型的方法目前在工業應用上難以突破。基于數據驅動的方法無需考慮鋰離子電池內部退化機理，只需要通過狀態監測技術獲取鋰離子電池蘊含退化信息的歷史數據，再利用統計回歸或機器學習等方法構造退化模型來實現剩余壽命預測。人工神經網絡、支持向量機(SVM)和相關向量機(RVM)等方法已被用于鋰離子電池剩余壽命預測。但神經網絡方法存在計算復雜度大，易陷入局部最優解，動態更新能力差等問題；而SVM和RVM最優核參數的確定是需要解決的難題。

極端學習機是2006年由Huang等提出的一種新型單隱層前饋神經網絡(SLFNs)，已成功應用于回歸和分類領域。但是在使用過程中，由于隱層權值和偏差隨機生成會造成一定概率的復共線性問題，造成ELM預測性能存在不確定性，從而影響ELM的泛化性能。

針對上述問題，為提高極端學習機預測鋰離子電池剩余壽命的可靠性，本文提出采用人工魚群算法對ELM網絡參數進行優化，并針對基本魚群算法收斂速度慢、易陷入局部最優的問題提出改進方案，實現最優ELM隱含層網絡參數的提取，建立鋰離子電池剩余壽命預測模型，最后通過NASA Ames研究中心的公開數據集對模型性能進行驗證。

極端學習機相比傳統的BP神經網絡、RBF神經網絡，將參數訓練的迭代調整過程轉化為求解線性方程組，解析求得具有最小范數的最小二乘解作為網絡權值，整個訓練過程可一次完成無需迭代，這使得ELM的訓練速度獲得了顯著提升。ELM的回歸原理可歸納為

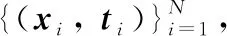
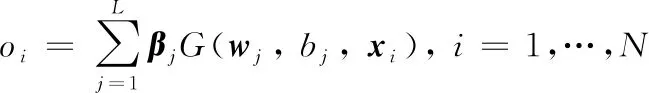
(1)

其中=[1,2,…,]是連接第個隱層神經元和輸入神經元的權向量，=[1,2,…,]是連接第個隱層神經元和輸出神經元權值向量，是第個隱層神經元偏差。

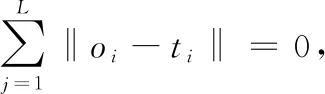
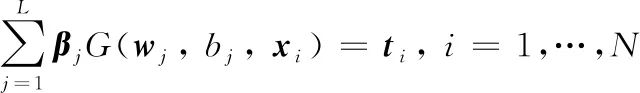
(2)

上式個方程可以簡寫為

=

(3)

其中

(,…,,,…,,,…，)=

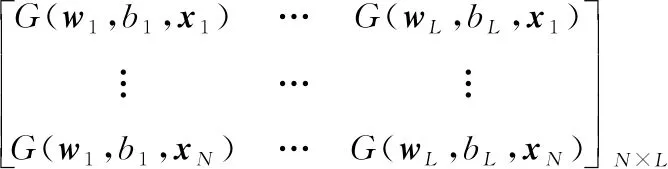
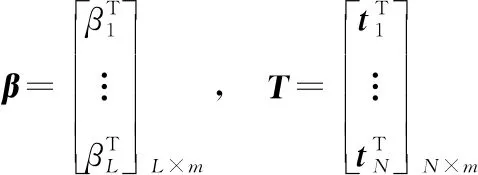
其中:稱為神經網絡的隱層輸出矩陣；的第列表示第個隱層節點關于,,…,的輸出矩陣。

=

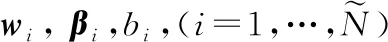
(4)

式(4)中=[,…,]，是矩陣的Moore-Penrose廣義逆。

綜上，給定一個訓練樣本集給定訓練集，激活函數()，隱層節點數目為。ELM學習算法步驟為：

Step 1：隨機指定輸入權值和隱層偏差，=1,…,；

Step 2：計算隱層輸出矩陣；

Step 3：計算輸出權值。

針對可能因ELM隱層輸出矩陣出現病態導致偽逆計算結果錯誤，本文借鑒嶺回歸的思想，將式(4)輸出權值的求解替換為式(5)所示形式：

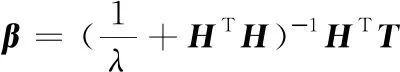
(5)

其中為正則化參數。

3 人工魚群算法及改進

3.1 基本人工魚群算法

人工魚群算法(AFSA)是基于自然界中魚群覓食行為提出的一種智能優化方法。其核心算法主要包括3種行為：覓食、聚群和追尾。在實際應用中，將每條人工魚視為問題的一個可行解，通過適應度函數評估每個解的優劣。具體尋優過程如下：

設人工魚初始規模為，每條魚的位置表示為=[,,…,]。食物濃度函數，即適應度函數定義為=(),=1,2，…,，任意兩條魚和之間的距離為=‖-‖，其中‖·‖為歐幾里得范數。在每個迭代過程中，人工魚通過覓食、聚集和追尾行為進行位置更新。

1) 覓食行為。假設一條人工魚當前位置為，對應的適應度值為=()。在該人工魚感知范圍內隨機選擇另一位置，若對應的適應度函數值滿足>，那么人工魚就按照式(6)朝移動一步。否則，人工魚在感知范圍內再隨機選擇其他位置重新判斷是否滿足條件，若嘗試次仍不滿足前進要求，此時人工魚就根據式(7)隨機選擇一個移動位置。

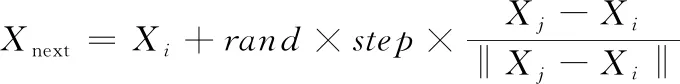
(6)

=+×

(7)

其中為[0,1]區間的隨機數，為移動步長。

2) 聚群行為。假設在以為中心的感知范圍內共有條魚。如果≥1，那么根據式(8)計算得到當前感知范圍內中心位置。此時如果滿足>(為擁擠度因子)且>，就說明中心位置更優且周圍不擁擠，那么就根據式(9)計算下一位置。否則，執行覓食行為。

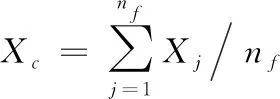
(8)

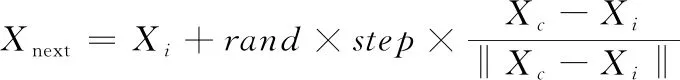
(9)

3) 追尾行為。假設在當前感知范圍內找到的具有最大適應度值的人工魚位置為，對應的適應度值為。如果滿足>且>，說明位置更優且位置周圍不擁擠，那么人工魚根據式(10)朝著移動一步。否則，執行覓食行為。

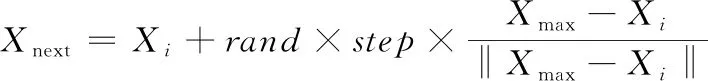
(10)

3.2 加速魚群算法

基本魚群算法在尋優過程中存在如下的問題：一是在整個進化過程中采用固定的感知范圍和移動步長不利于前期快速全局尋優和后期精確局部定位；二是在覓食過程中，達到設定的最大嘗試次數，仍然不滿足移動條件，就在感知范圍內隨機移動一步，這無法保證移動后的位置優于當前位置，且易造成陷入局部最優。

針對上述問題，本文提出相應的改進方案：一是將感知范圍和移動步長由固定值改為動態值，隨著進化代數自適應調整，以保證前期快速收斂和后期精確尋優。改進后的和移動步長根據式(11)和(12)確定。

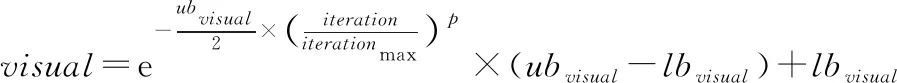
(11)

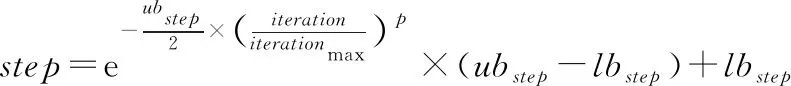
(12)

其中:、，、分別為感知范圍和移動步長的上、下限，為當前代數，為最大代數。

二是在覓食過程中，當達到最大嘗試次數仍無法滿足移動條件時，給隨機移動增加一個混沌擾動，以增加種群多樣性并提高跳出局部最優的能力。改進后的隨機移動位置根據式(13)確定。

=+×sin(2)×

(13)

通過上述改進，可實現在加快魚群收斂速度的同時提高收斂精度。

4 加速魚群算法優化極端學習機的預測建模過程

基于上述改進思路，利用AAFSA-ELM進行預測建模的流程如圖1所示。

具體建模步驟歸納如下：

Step 1：初始化人工魚群參數，主要包括種群規模，感知范圍上、下限，移動步長上、下限，迭代次數，嘗試次數等；

Step 2：利用Tent混沌映射函數生成2倍指定規模的種群，基于訓練樣本和適應度函數初篩出適應度值較大的前個作為初始種群；

Step 3：魚群執行覓食、聚群和追尾行為，執行過程中人工魚感知范圍和移動步長按照式(11)和式(12)自適應確定，當人工魚不滿足移動條件時，按照式(13)進行增加混沌擾動的隨機移動；

Step 4：判斷是否達到最大迭代次數，若未達到，返回Step 3，否則，轉向Step 5；

Step 5：輸出最優隱層參數和，送入ELM構建預測模型；

Step 6：利用測試樣本對預測模型性能進行驗證，輸出鋰離子電池剩余壽命預測結果。

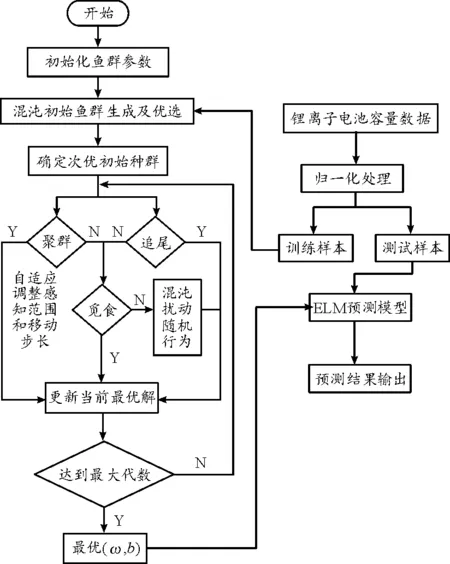
圖1 AAFSA-ELM預測建模流程框圖

5 實驗驗證

選擇NASA Ames研究中心的公開數據集。用于老化測試的鋰離子電池為標稱容量為2 Ah的18650型鋰離子電池，數據集共包含標號分別為B0005、B0006、B0007、B0018的四塊電池，分別記為B5、B6、B7、B18。4塊電池在24 ℃的室溫條件下，先以1.5 A的恒流電流進行充電，直到電池電壓達到4.2 V后轉為恒壓模式繼續充電，待充電電流下降至20mA以下停止充電。隨后，以2 A恒流方式對電池進行放電，直到四塊電池電壓分別降至2.7 V、2.5 V、2.2 V、2.5 V，至此完成一個充放電循環周期，重復上述循環過程直至電池壽命終止。通過剔除異常值后分別提取得到B5、B6、B7、和B18四塊電池循環過程168個、168個、168個和132個電池容量數據。

仿真實驗中，分別利用未經優化的ELM和AAFSA-ELM建立預測模型。為檢驗預測模型泛化性能，分別選擇四塊電池容量數據的40%和50%作為訓練樣本進行網絡訓練，剩余樣本作為測試樣本驗證預測模型性能。仿真過程中各參數設置如表1所示。

預測過程中，B5、B6、和B18三塊電池壽命失效閾值設為當電池容量下降至標稱容量的70%， B7設置為下降至標稱容量的72%。分別利用ELM和本文提出的AAFSA-ELM建立預測模型，并與文獻[18]中的ALO-SVR方法進行比較，預測結果如表2所示。

表1 參數設置

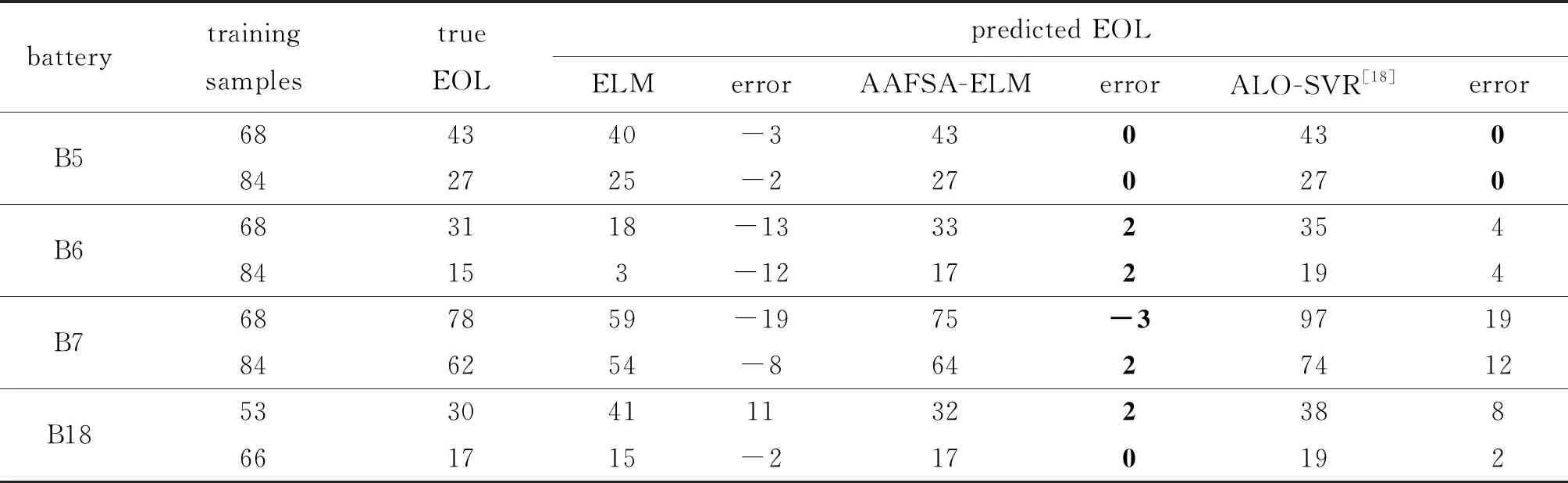
表2 ELM和AAFSA-ELM剩余壽命預測結果

從表2可以看出，AAFSA-ELM預測結果誤差最小，最大預測誤差為3，而ALO-SVR和ELM最大誤差為19，但ELM因復共線性問題使得其難以提供穩定精確的預測結果，AAFSA-ELM方法預測結果明顯優于ELM和ALO-SVR。

圖2～圖9為采用ELM和AAFSA-ELM分別利用總樣本的40%和50%進行訓練，其余作為測試樣本的預測結果曲線。

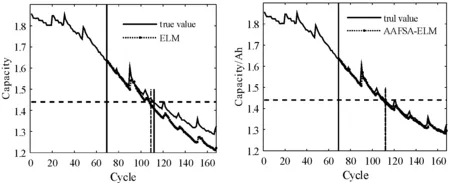
圖2 B5電池40%總樣本訓練時預測結果曲線

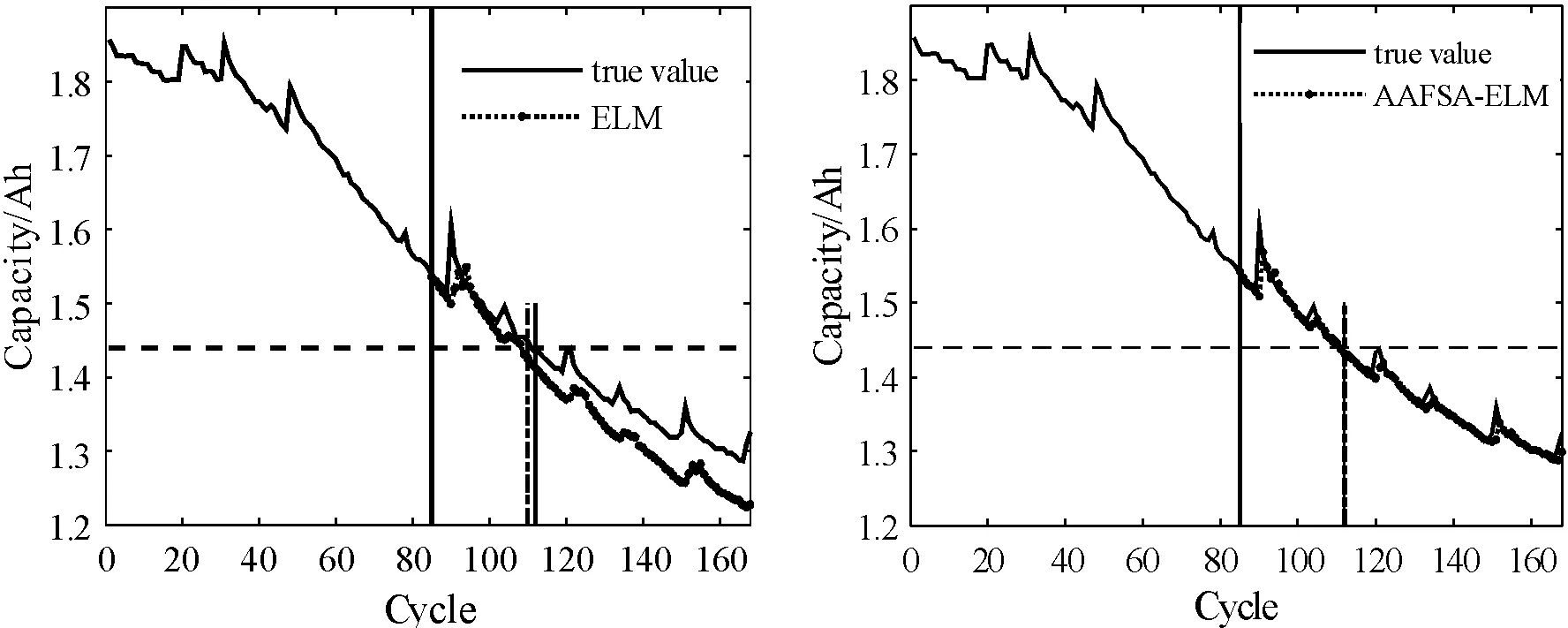
圖3 B5電池50%總樣本訓練時預測結果曲線

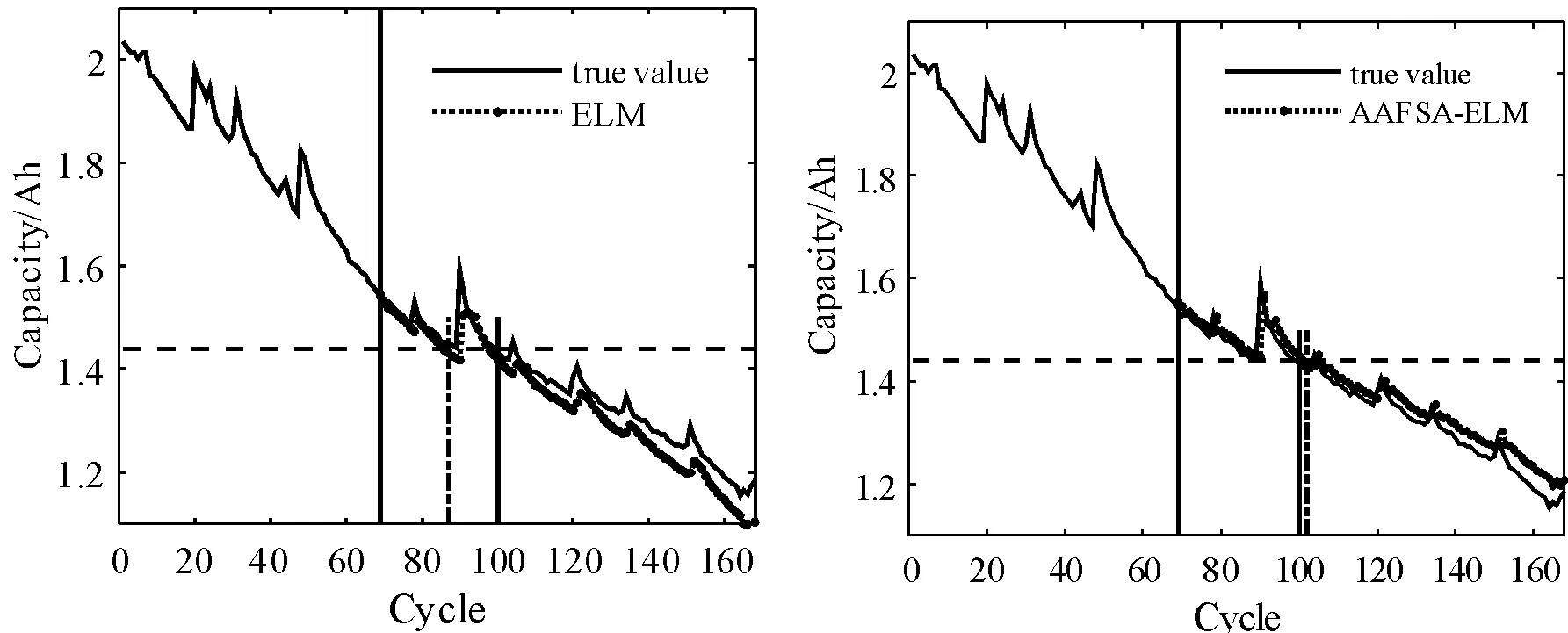
圖4 B6電池40%總樣本訓練時預測結果曲線

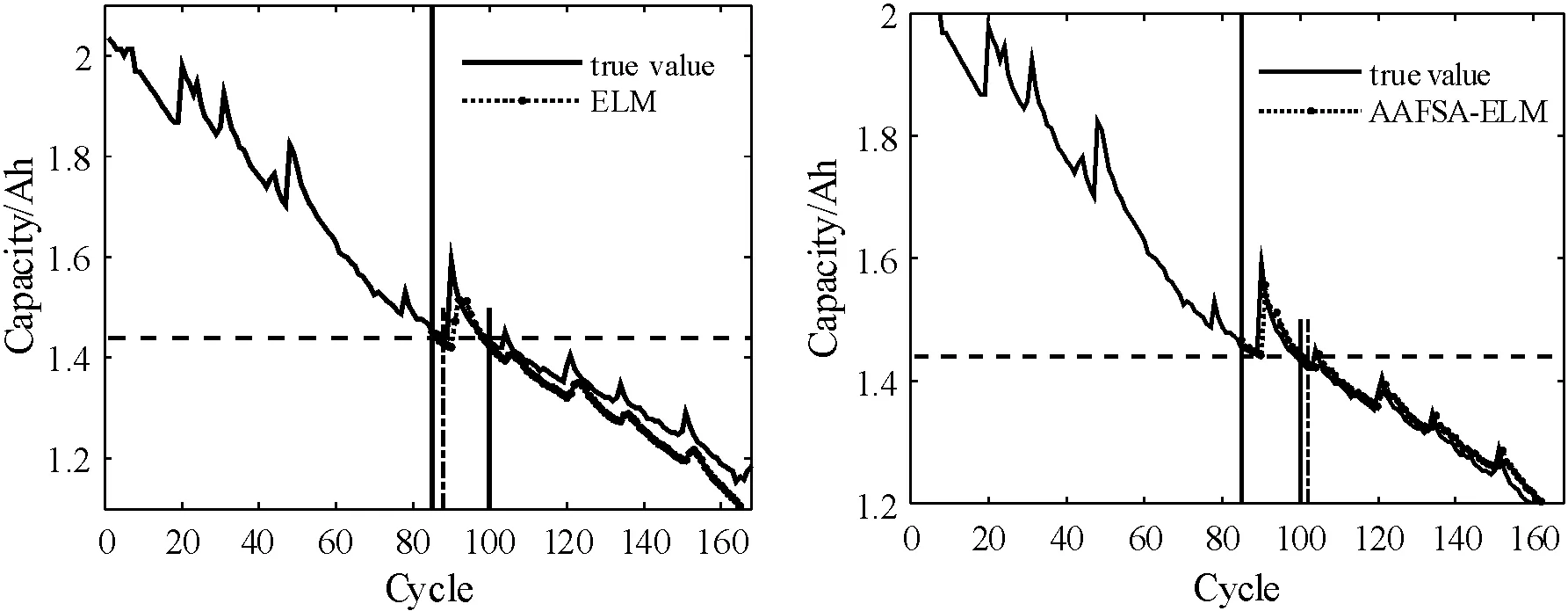
圖5 B6電池50%總樣本訓練時預測結果曲線

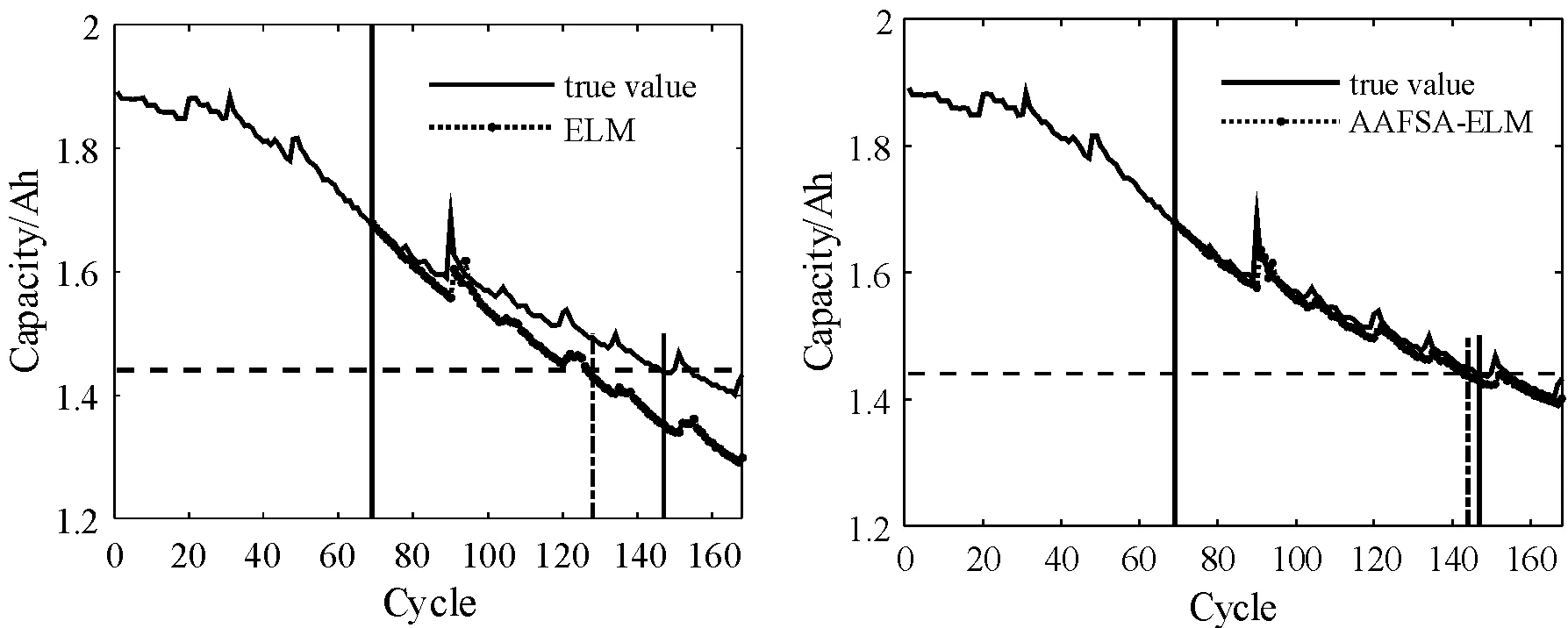
圖6 B7電池40%總樣本訓練時預測結果曲線

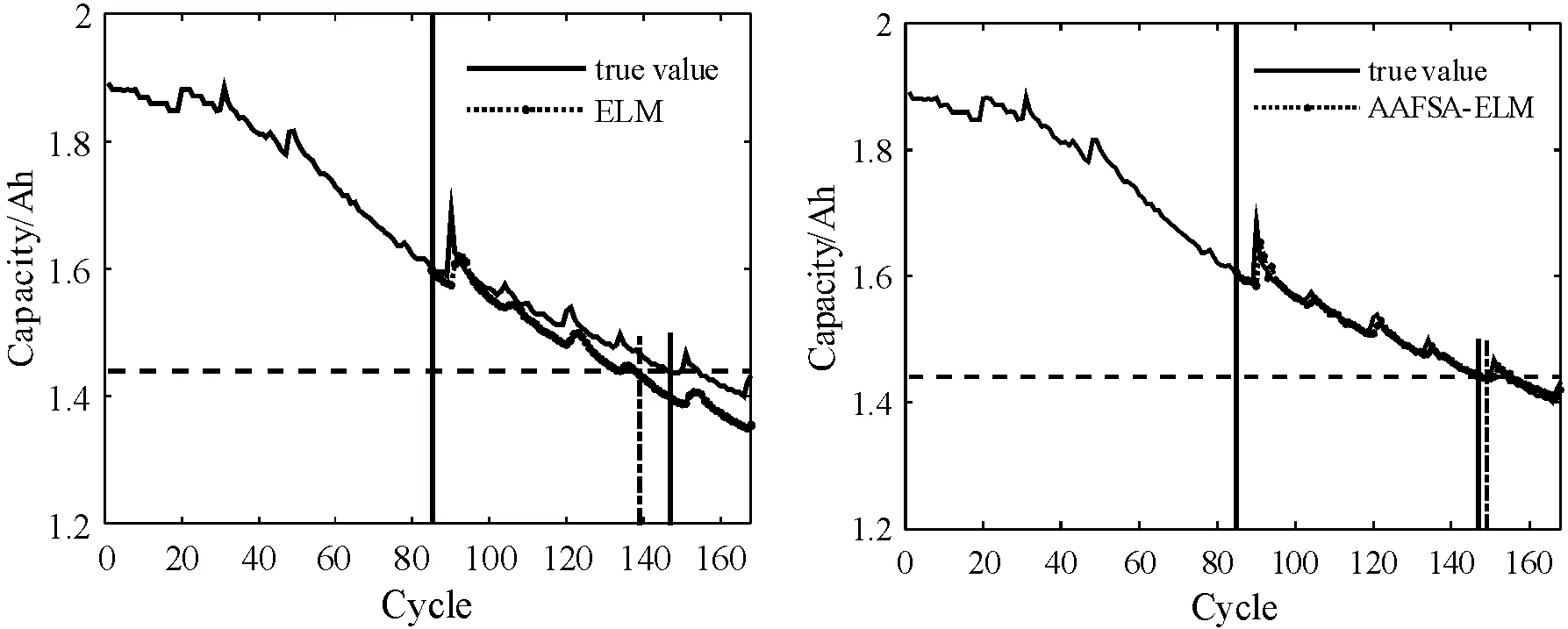
圖7 B7電池50%總樣本訓練時預測結果曲線

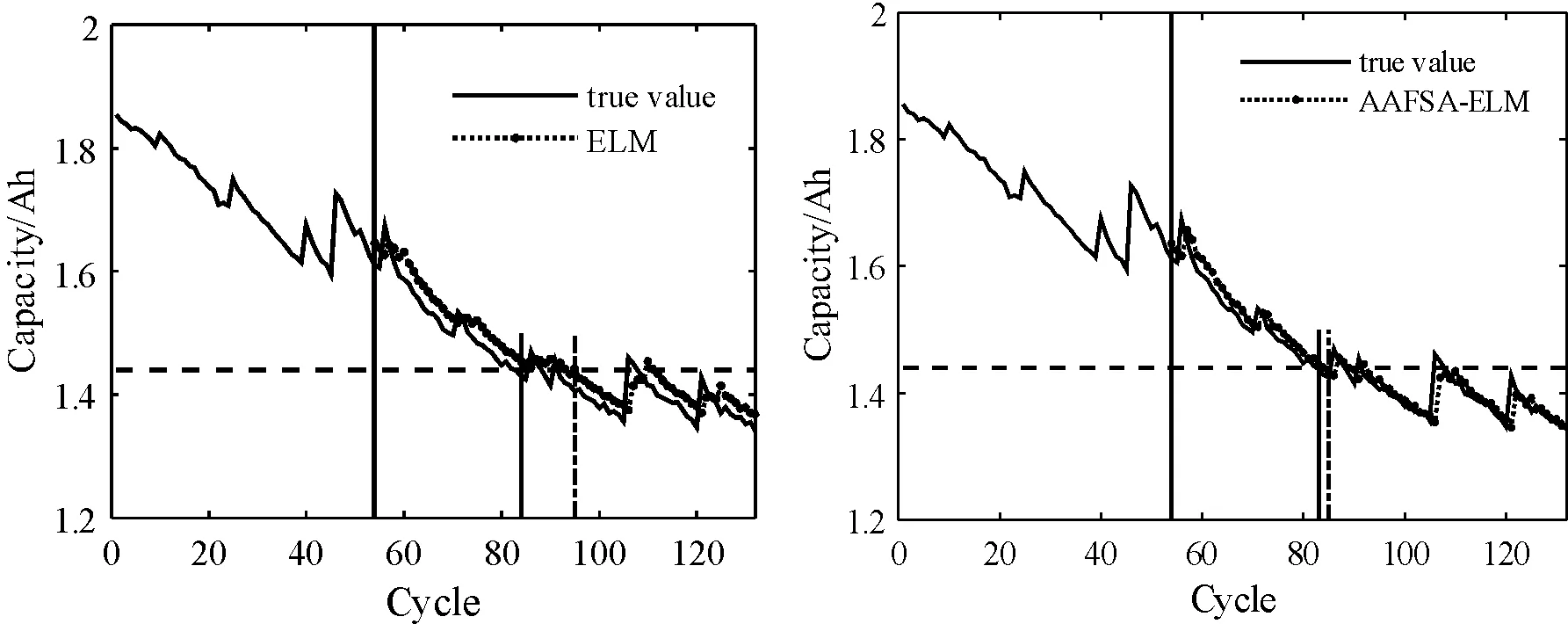
圖8 B18電池40%總樣本訓練時預測結果曲線

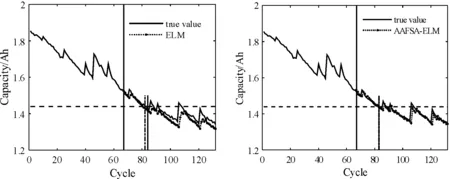
圖9 B18電池50%總樣本訓練時預測結果曲線

可以看出：ELM和AAFSA-ELM都能夠跟蹤到鋰離子電池性能退化狀態，但是ELM方法由于隨機生成隱層權值和偏差，無法保證以最優的精度跟蹤退化過程，網絡泛化性能存在不確定性。而經AAFSA參數優化后，ELM始終能夠以最優參數實現鋰離子電池剩余壽命預測，泛化性能顯著提高，跟蹤電池退化狀態效果良好。

為進一步比較不同方法的預測性能，分別列出平均絕對誤差(Mean Absolute Error，MAE)和均方根誤差(Root Mean Square Error，RMSE)對各方法的預測結果，如表3所示。可以看出：本文提出的AAFSA-ELM方法預測結果的MAE和RMSE明顯優于其他3種方法，而ELM方法的預測精度也優于SVR方法。例如對于B6電池，AAFSA-ELM預測結果的MAE和RMSE相比ALO-SVR降低了近50%，ELM與SVR預測結果也能得到類似結論。

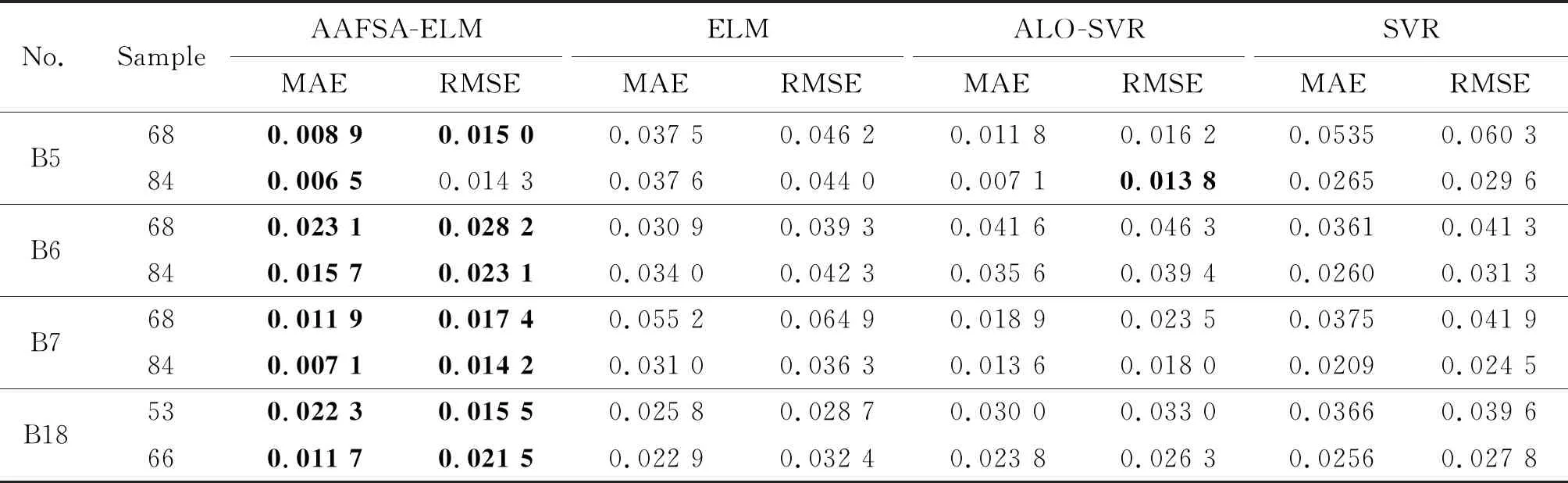
表3 不同預測模型性能比較

圖10所示為以B18鋰離子電池為例，分別采用AFSA和AAFSA對ELM隱含層參數尋優的收斂曲線，可以看出，以40%樣本數或者50%樣本數作為訓練樣本時，AAFSA的收斂速度和跳出局部搜索能力都要優于AFSA。

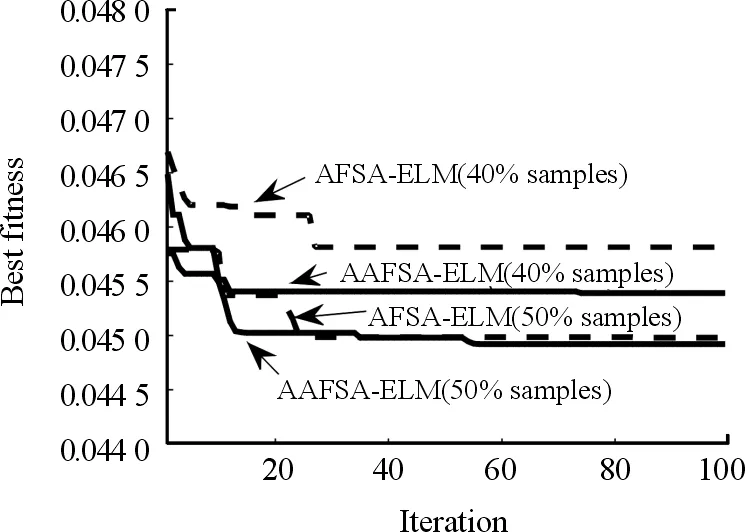
圖10 AFSA與AAFSA網絡訓練收斂曲線Fig.10 Network training convergence curve of AFSA and AAFSA

6 結論

1) 鋰離子電池安全問題已引發廣泛關注，準確的剩余壽命預測模型能夠幫助使用者提前掌握鋰離子電池健康狀態，預防性能退化導致的電池失效。

2) 基于數據驅動方法，針對ELM因隱含層權值和偏置隨機生成引起預測結果振蕩的問題，采用AFSA優化隱含層輸入參數，并針對基本AFSA方法收斂速度慢、易陷入局部最優的問題進行改進，實現對ELM隱含層權值和偏置的優化，獲得最優ELM網絡結構。

3) 利用提出的最優ELM構建NASA Ames研究中心的4塊18650鋰離子電池剩余壽命預測模型：相比未優化的ELM方法，本文模型的預測結果更加穩定可靠，相比SVR及其改進方法在精度上具有顯著優勢，可為實現鋰離子電池剩余壽命精確預測提供支持。