高負荷動力渦輪葉型優化研究

陳 晨，李 維

(1.中國航發湖南動力機械研究所，湖南 株洲 412002；2.中小型航空發動機葉輪機械湖南省重點實驗室，湖南 株洲 412002)

0 引言

就航空渦軸/渦槳發動機而言，動力渦輪是發動機的一個重要核心部件，由于受到傳動系統的限制，相比于燃氣渦輪，動力渦輪轉速低，尺寸大，級數多，且由于葉輪外徑大，單排葉片數量也要遠高于燃氣渦輪。因此在動力渦輪中采用高負荷葉型設計(Zweifel系數大于1[1])，能夠有效減少葉片數，降低制造成本和渦輪部件重量，提高航空渦軸/渦槳發動機的功重比。

然而葉型負荷的提高勢必增大吸力面逆壓梯度，使得附面層易于分離，且葉片負荷大小以及負荷分布規律直接影響動力渦輪葉片通道內由壓力面指向吸力面的橫向壓力梯度[2]，而橫向壓力梯度是形成動力渦輪內部復雜渦系結構的驅動力。因此理清葉片表面負荷分布對流動損失的影響機理，有助于為高性能高負荷動力渦輪的設計提供理論支撐。

隨著對高負荷動力渦輪內部流動結構的理解認識不斷加深，高負荷動力渦輪葉片應該設計成何種載荷分布方式能夠有效抑制附面層和端區的流動分離是目前研究的一個熱門課題。Zoric[3]等人分別針對Pack B(后加載，Zw=1.08)、Pack D-A(后加載，Zw=1.4)和 Pack D-F(前加載，Zw=1.4)三套葉柵進行實驗測量發現：后加載葉型Pack D-A 相比于前加載葉型Pack D-F 具有較高的葉型損失，但前加載葉型Pack D-F表現出較強的通道渦和二次湍動能，導致二次流損失增強。Weiss和Fottner[4]以前加載葉片和后加載葉片為研究對象，也得出相似的結論，主要原因是前加載葉片通道前端具有較強的橫向壓力梯度，導致較多的端區低能流體卷入通道渦，而后加載葉片由于最大壓力梯度位置在葉片喉部附近，引起較少的端區邊界層卷入通道渦。

綜上分析發現，大多研究學者的觀點都更傾向于前加載葉片設計增加了端區二次流損失，但一般具有較好的二維氣動性能；后加載葉片端區二次流損失相對較小，但吸力面附面層更容易分離，葉型損失有所增加。本文通過對某高負荷動力渦輪第一級導葉進行前加載、中間加載、后加載三種方案的葉型優化，研究分析三種載荷分布方案對渦輪內部流動損失影響規律，從而指導高負荷動力渦輪的葉型優化設計

1 研究對象與數值計算方法

1.1 研究對象

以某型高負荷動力渦輪第一級導葉為研究對象，保證喉部寬度、出口有效角一定的情況下，通過調整前緣直徑、尾緣直徑、軸向寬度、安裝角、進口構造角、出口構造角、尾緣楔角等葉型幾何參數對葉片進行前加載、中間加載、后加載三種方案的葉型優化，中截面(50%葉高處)主要葉型幾何參數見表1，中截面沿葉片表面馬赫數分布曲線見圖1，從圖1可以看出，優化后的葉型吸力面逆壓梯度大幅度下降。

表1 主要葉型幾何參數

1.2 數值計算方法

1.2.1 計算方法及邊界條件

本文使用商業流體計算軟件CFX求解三維定常雷諾平均N-S方程。湍流模型選取標準k-ε兩方程湍流模型，湍流項的離散采用一階精度格式，對流項離散采用高階精度格式。

計算時保證計算域的進、出口邊界條件相同，進口給定絕對總溫、總壓、進口氣流角徑向分布，出口給定平均靜壓，葉型表面采用無滑移壁面邊界，考慮葉片和上下端壁等固壁粗糙度的影響，設置固壁粗糙度的等沙粒直徑為0.02 mm，計算域柵距方向邊界采用周期性邊界條件。

1.2.2 計算網格

計算域為一個兩級的動力渦輪，計算網格由numeca軟件生成，網格為非結構化網格，第一級導葉局部網格示意如圖2所示，對葉片和上下端壁附近的網格進行加密，保證近壁面處y+小于10，通過網格無關性驗證，設置展向網格節點數為73，計算域總網格數為333萬左右。

2 計算結果與分析

2.1 高負荷葉型優化前后對比

從圖1的葉片表面馬赫數分布曲線可以看出，未優化的高負荷葉型馬赫數峰值很高，吸力面沿流向的逆壓梯度很大，導致附面層分離，層流分離區域，馬赫數分布曲線呈“平臺”狀，三種優化方案的馬赫數峰值均大幅度下降，且加速后馬赫數曲線未出現“平臺”狀分布。圖3為未優化葉型及三種優化方案葉片表面極限流線圖，未優化的高負荷導葉在沿葉高30%至90%區域葉片表面產生明顯的漩渦結構，表明附面層在吸力面發生了嚴重的分離現象，經過優化后，三種載荷分布形式的葉型吸力面分離現象均消失，端壁附近偏離主流方向的區域面積減小，且隨載荷后移偏離主流方向區域面積越小。

四個狀態的氣動性能參數如表2所示，三種方案優化后的渦輪效率均有大幅度提高，能量損失系數下降，且中間加載方案的總壓恢復系數和渦輪總效率最高，能量損失系數最低，具有更優的氣動性能。

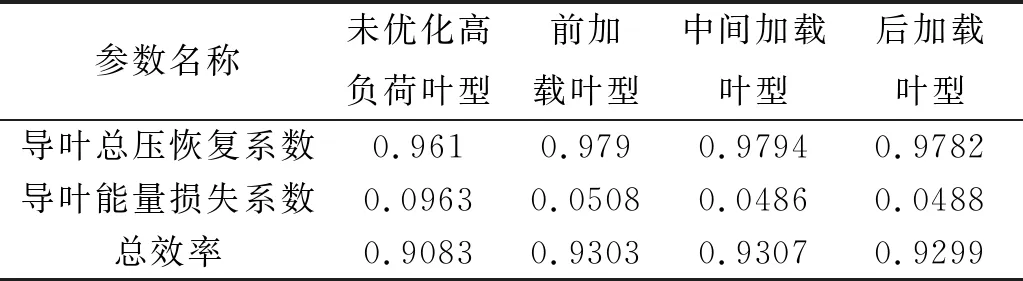
表2 氣動性能參數表

2.2 載荷分布對葉型損失的影響

如圖1馬赫數曲線表明，三種方案的馬赫數峰值相當，前加載葉型加速區域所處的流線范圍約為0～0.2，中間加載加速區域所處的流線范圍約為0～0.5，后加載葉型加速區域所處的流線范圍約為0～0.7，在加速區域內后加載葉型馬赫數變化最平緩，前加載葉型馬赫數變化最快，加速區域后前加載葉型的馬赫數變化最平緩，后加載葉型馬赫數下降最快，說明前加載葉型在沿流線上游區域壓力梯度最大，在沿流線下游區域壓力梯度最小；后加載葉型在沿流線上游區域壓力梯度最小，在沿流線下游區域壓力梯度最大。因而前加載葉型在上游區域葉型損失大，下游區域葉型損失小；后加載葉型在上游區域葉型損失小，在下游區域葉型損失大。圖4為三種方案沿流向的葉型損失變化曲線圖，本文葉型損失定義為(P1*-P2*)/P1*-P1，其中P1*為進口總壓，P2*為所在截面處的總壓，P1為進口靜壓，葉型損失沿流向變化曲線圖與上述分析一致，在沿流向0～0.5范圍內前加載方案的葉型損失最大，流向位置0.5以后前加載方案葉型損失增加速率降低，最后總葉型損失與中間加載方案相當；在沿流向0.7～1范圍內，后加載方案葉型損失劇增，總葉型損失最大。

2.3 載荷分布對二次流損失的影響

圖3葉片表面極限流線圖表明，隨著載荷分布向后移動，端區附近偏離主流方向區域面積逐漸減小，表明載荷分布約靠后，端區二次流越小。

圖5為沿流向的徑向氣流角分布圖，從圖5中可以看出，后加載葉型在整個流動過程中氣流角沿徑向偏轉較小，前加載葉型在沿流向50%位置以前沿徑向的氣流角偏轉程度比中間加載葉型大，沿流向50%位置以后沿徑向的氣流角偏轉程度比中間加載葉型小。圖6為沿流向湍動能云圖，如圖6所示，在沿流向50%位置以前前加載葉型端壁處的湍動能比中間加載葉型的高，沿流向50%位置以后前加載葉型端壁處的湍動能比中間加載葉型的低，后加載在下游位置葉中區域的湍動能明顯增大。本文用二次流動能(Ske)來定義通道內二次流的大小(Ske=1/2*ρoutlet(r，φ)*|vsec(r，φ)|2)，將出口質量平均速度定義為該出口處的主流速度，vsec(r，φ)為導葉出口處每一點的實際速度與該主流速度作矢量減法，ρoutlet(r，φ)為導葉出口處的當地密度，表3為三個優化方案的出口質量加權平均二次流動能，數據表明，前加載葉型通道內總的二次流損失最大，其次是中間加載葉型，后加載葉型的二次流損失最小。

表3 出口質量加權平均二次流動能

3 結論

本文對未優化的高負荷葉型、前加載優化葉型、中間加載優化葉型、后加載優化葉型進行了三維計算分析，分析了高負荷動力渦輪葉型的氣動性能以及流動損失產生的機理，研究了葉片表面負荷分布對流動損失的影響。綜合以上分析，可以得出以下結論：

1)隨著葉片負荷的升高，吸力面馬赫數峰值增大，吸力面逆壓力梯度增大，導致吸力面容易發生附面層分離現象，進而增加了葉型損失，同時端區橫向壓力梯度也會更大，使得端區二次流增大，從而導致高負荷動力渦輪通道內的流動結構更為復雜。

2)通過設置合適葉型幾何參數，可以優化葉型表面的負荷分布，使吸力面馬赫數峰值降低，從而減小吸力面逆壓力梯度，消除附面層分離現象，大幅度降低葉型損失。

3)葉片表面載荷分布方式對流動損失有一定的影響，前加載葉型設計具有較好的二維氣動性能，產生較大影響，壓強降低又會使燃氣發生器做功效率下降。為了避免出現這種情況，對裝填式管狀藥柱異常燃燒機理進行研究。從藥柱結構特性和燃氣發生器燃燒室結構特性發現，前端燃氣流速較小，基但通道內上游區域的端區二次流損失相對較大，后加載葉型設計通道內端區二次流損失較小，但通道內下游區域的葉型損失較大，中間加載葉型通道內下游區域端區二次流損失比前加載大，但總二次流損失比前加載葉型小，且葉型損失與前加載葉型設計相當，因此中間加載優化方案具有更優的氣動性能。