多徑信號相關與信道相關陣列空間譜估計性能

李忠

（中國電子科技集團公司第二十二研究所，河南新鄉 453003）

移動通信信號傳輸過程中，由于空間存在反射、散射、繞射等現象，存在大量的多徑信號，形成多徑信道信號傳輸。同一用戶形成的多徑信號通常被認為是相關的或相干的。在多徑信道的信號傳播環境下，由于信號相干或相關，一般子空間類算法[1-2]如MUSIC、ESPRIT 等信號子空間的秩降低，對多徑相干信號DOA 的估計性能下降。為了解決多徑相干信號的DOA 估計，相關的文獻中提出了多種去相干處理方法，基本處理方法有兩大類[3]，一類是降維處理，另一類是非降維處理。降維處理方法主要是空間平滑算法、修正MUSIC（MMUSIC）和矩陣重構算法等[4-9]，其中常用的空間平滑類處理算法可以分成前向空間平滑算法(FSS)、后向平滑算法(BSS)、前后向平滑算法(FBSS)；非降維處理方法主要有Toeplitz方法等[10]。信號通過多徑信道傳輸不僅存在多徑相干信號，同時接收陣列中不同接收信道存在信道的相關性。信道的相關特性由信道的空間特性和天線陣的配置共同決定。兩個天線接收到的信號一般是相關的，其相關系數與天線距離和入射波的角度譜有關。目前關于信道的相關研究文獻較多[11-12]，且主要以通信系統性能的影響研究為主[13-15]。在實際信號偵測系統中[16]，接收天線信道的相關性對信號測向性能具有一定影響，信道相關性對DOA 估計性能的影響未見相關文獻研究。若不僅考慮到信號的相干性，同時考慮接收信道存在相關性，對DOA 估計性能又如何？文中從多徑相關信號的DOA 估計性能出發，重點考慮信道相關性對DOA 估計的影響，引入相關系數矩陣，給出了陣列協方差矩陣形式，分析存在信道相關性情況下，對DOA 估計的影響；并綜合分析存在信號相關與信道相關雙重因素下，多徑信道的DOA 估計性能，為信息系統DOA 性能評估提供指導。

1 信號的相關性

兩個平穩信號si(t)和sl(t)之間的相關系數為：

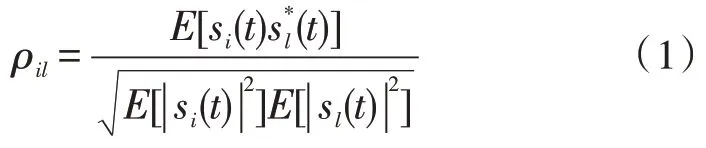
將信號之間的相關性定義為：

根據以上定義，假設K個相干源，其形式為：

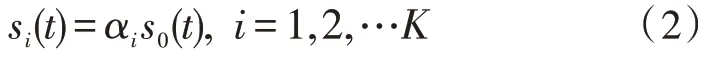
設αi為第i個信號相對于s0的衰落系數，陣列的輸出矢量為：

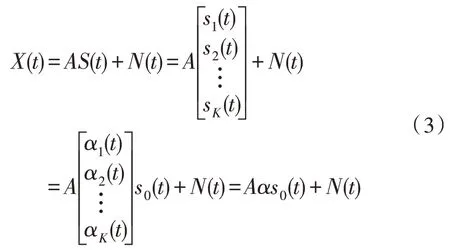
式中，N(t)為噪聲矩陣，A為陣列流型矩陣，A=[a(θ1),a(θ2),…,a(θK)]，其中，a(θ1),a(θ2),…,a(θK) 為導向矢量。

2 信道相關性

由于接收信道天線之間的相互影響以及多徑入射波信號存在空間譜擴展，接收信道存在空間相關性，存在信道相關性條件下，陣列流型矩陣將A變為：

式中，r為信道相關系數矩陣，陣列接收矩陣如下：

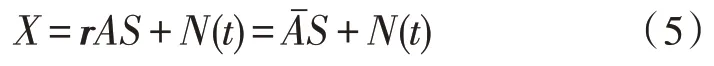
將陣列中第m個陣元和第n個陣元接收信號的空間相關性定義為：

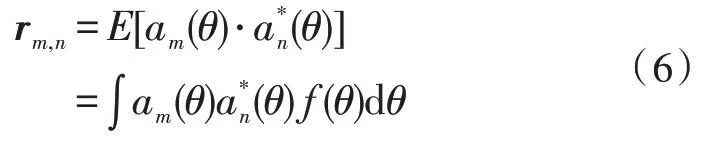
式中，am(θ)、an(θ)為陣列流型矩陣A的導向矢量元素，f(θ)為入射信號概率密度角分布函數。均勻直線陣情況下，陣元間距為d(d＜λ/2）。

1）假設入射角概率分布服從高斯分布，分布函數滿足：

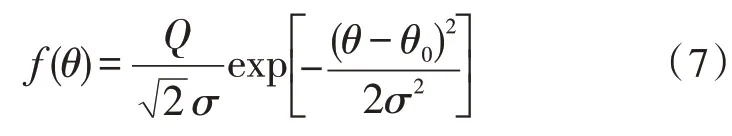
式中，θ∈[θ0-Δ,θ0+Δ]，Δ 為角度擴展，θ0為中心到達角，誤差系數σ為分布的標準差。

2）假設入射角概率分布服從均勻分布，分布函數滿足：

將分布函數代入相關系數積分表達式中，在角度擴展較小的情況下，cos Δ ≈0，sin Δ ≈0，根據式（6），計算結果如圖1～3 所示。

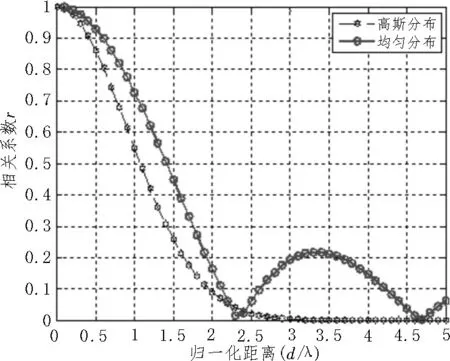
圖1 不同分布下空間相關性隨陣元間距波長比的變化（σ=10°，θ0=45°）

通過圖1 可以看出，不同的入射角概率分布模型中，陣元相關性隨陣元間距增加而產生明顯的差異性。以常見的高斯分布為例，圖2 與圖3 表明，在相同陣元距離和入射中心角θ0的條件下，標準差σ越小，空間相關性越高；相同陣元距離和標準差σ的條件下，入射中心角θ0越大，空間相關性越高。

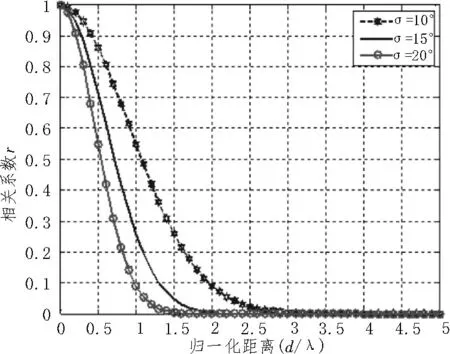
圖2 相同入射中心角下空間相關性隨陣元間距波長比的變化（θ0=45°）

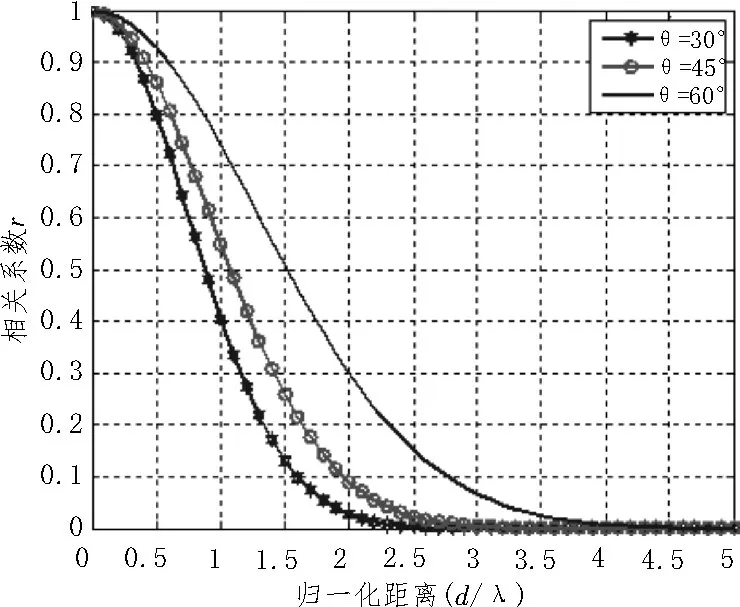
圖3 不同入射中心角下空間相關性隨陣元間距波長比的變化（σ=10°）

作為實例，圖4 給出了2×2 MIMO 系統的信道容量隨SNR變化的曲線，針對不同的發射端相關系數α和接收端相關系數α，對比完全獨立的MIMO 信道(α=β=0)與完全相關的信道(α=β=1.0)，獨立不相關信道的信道容量MIMO 容量大幅提高。

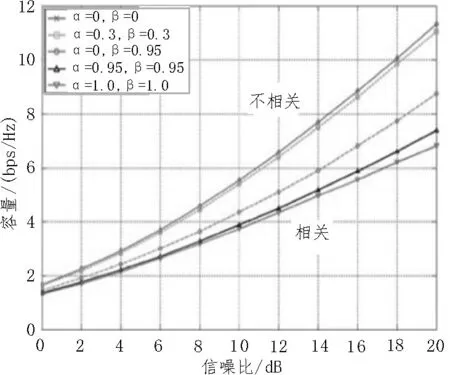
圖4 不同發射和接收相關系數情況下，2×2 MIMO系統的平均信道容量隨信噪比的變化曲線

3 雙重因素綜合存在情況下的DOA估計

3.1 相關/相干信號DOA估計

考慮到信號的相關性或相干性，陣列協方差矩陣由式（9）可得：

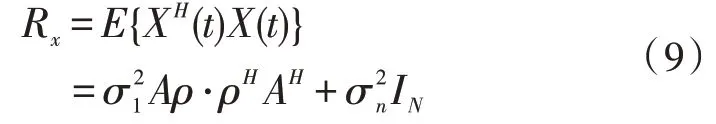
式中，為相對信號功率，ρ?ρH可以看作信號相干系數矩陣。

通過該陣列協方差矩陣構造MUSIC 譜函數進行DOA 估計。

設陣元數N=8；陣元間距d=λ/2；入射信號數K=3，入射角θ=[5°,10°,15°]。快拍數為1 000，信噪比SNR=20 dB。

情況一：信源s1與信源s2相關，信源s3獨立；信源s1衰落因子為1；信源s2衰落因子為0.8，相移π/6。

情況二：信源s1、s2、s3相互獨立。

以上兩種情況下計算的空間譜結果如圖5所示。

圖5 信號獨立與信號相關空間譜分布

從圖5 中可以看出，相互獨立的信號均能獨立分辨估計，若假設接收信號s1、s2存在相關性，除了獨立信源s3(θ=15°)明顯可分辨外，兩相關信源s1、s2空間譜無法分辨，陣列譜估計性能降低。

3.2 信道相關性DOA估計

若考慮到信道的相關系數矩陣后，陣列協方差矩陣由式（5）可得：

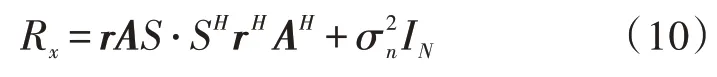
其中，r為文中引入的相關系數矩陣：

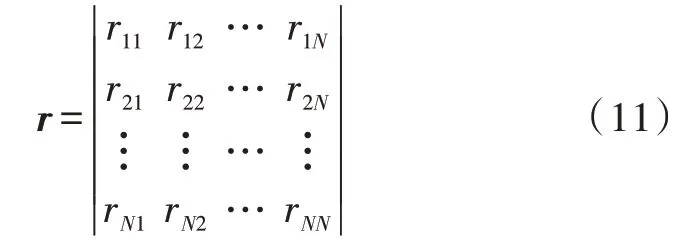
相關系數矩陣元的求解見式（6）。

通過該陣列協方差矩陣構造MUSIC 譜函數，并進行DOA 估計。

設陣元數N=8；陣元間距d=λ/2；入射信號數K=3，獨立信道下入射角θ=[5°,10°,15°]，快拍數為1 000，信噪比SNR=20 dB，相關信道入射信號角分布服從高斯分布，入射中心角θ0=10°，計算信道相關性對MUSIC 譜的影響結果,信道獨立與信道相關空間譜分布如圖6 所示。

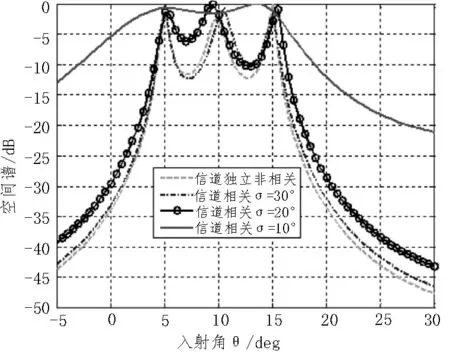
圖6 信道獨立與信道相關空間譜分布

從圖6 中可以看出，在相同陣元距離和入射中心角θ0=10°的條件下，隨著標準差σ越小，空間相關性越高，由于信道相關性增加，陣列的空間譜分辨率顯著惡化；同樣，通過分析得知，在相同陣元距離和標準差σ的條件下，入射中心角θ0越大，空間相關性越高。

3.3 雙重因素下的DOA估計

由相干信號協方差矩陣式（9）和考慮信道相關性的陣列協方差矩陣式（10）可知，雙重影響因素的情況下，陣列的協方差矩陣為：

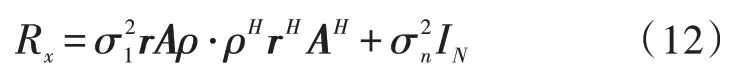
式中，為相對信號功率，r為相關系數矩陣，ρ?ρH可以看作信號相干系數矩陣，A為陣列流型矩陣。

通過該陣列協方差矩陣構造MUSIC 譜函數進行DOA 估計。假設計算條件如3.1 節與3.2 節信號相關與相關信道的情形，兩個因素綜合考慮后計算結果與3.1 節和3.2 節計算結果進行對比分析,信號相關與信道相關空間譜分布如圖7 所示。

圖7 信號相關與信道相關空間譜分布

從圖7 中可以看出，綜合考慮到信源的相關性與信道的相關性，兩個相關信源s1、s2無法分辨，第三個獨立信源s3(θ=15°) 譜峰也發生了明顯的偏移。計算結果表明，隨著標準差σ的減小，信道的空間相關性增大，空間譜甚至無法識別。由此可以看出，雙重因素影響下，陣列空間譜估計性能失效。

4 結論

文中通過分析計算表明，多經相關信號經過相關多徑信道接收，其DOA 估計不僅因缺秩造成信號無法分辨，甚至出現任何接收信號的DOA 都無法估計，導致譜估計分辨率與準確度顯著降低，甚至失效，由此產生的影響結果需要在工程設計中引起高度重視。系統設計中，可通過去相關技術消除信號的相干性，同時通過調整接收信道空間布局降低相關系數，降低信道相關性對測向系統的影響，避免雙重因素導致系統完全失效。