導數與三角“交會型”試題演繹出來的精彩

巨小鵬

(陜西省漢中市龍崗學校)

作為高考壓軸題,承擔著選拔人才功能的導數與三角函數結合的試題,能考查學生綜合能力和素養.新高考的考查已經不僅僅局限于基本知識和基本技能,更重視對學生綜合核心素養和關鍵能力的考查,題目會更加靈活多變,富有創新性和綜合性.在有限的題目里融入數學文化、生活實際,那么知識之間的融合必然會更加精彩,將不同的知識點融合交會,提高了難度,也考查了學生的綜合素養.導數與三角函數的精彩交會將是繼指數函數、對冪函數綜合交會之后的又一題型,于是周期性、有界性和放縮就被融入進來,在這個過程中,單調性、最值、極值、零點、取值范圍、恒成立和證明不等式等成了精彩交會的熱點.

1 恒成立問題

不等式恒成立問題常見方法:1)分離參數a≤f(x)恒成立(a≤fmin(x))或a≥f(x)恒成立(a≥fmax(x));2)數形結合;3)討論最值fmin(x)≥0或fmax(x)≤0恒成立;4)直接討論參數.

例1(2015 年湖南卷文21)已知a＞0,函數f(x)＝aexcosx(x∈[0,＋∞),記xn為f(x)從小到大的第n(n∈N*)個極值點.

(1)證明:數列{f(xn)}是等比數列;

(2)若對一切n∈N*,xn≤|f(xn)|恒成立,求a的取值范圍.

在解決數列與函數的綜合問題時,如果是證明題,要根據數列的定義明確證明的方向,如果是不等式恒成立問題,要使用不等式恒成立的各種不同解法(如變量分離法、最值法、因式分解法等)進行求解.總之解決這類問題要把數列看作特殊函數,并把它和不等式的知識巧妙結合起來綜合處理.

2 不等式證明問題

例2(2020年全國Ⅱ卷理21)已知函數f(x)＝sin2xsin2x.

(1)討論f(x)在區間(0,π)的單調性;

(2)證明:|f(x)|≤

(3)設n∈N*,證明:

(3)結合(2)的結論有

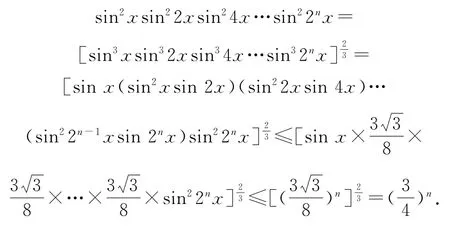
導數是研究函數的單調性、極值(最值)有效的工具,而函數是高中數學中重要的知識,對導數應用的考查主要從以下幾個角度進行:1)導數的幾何意義,往往與解析幾何、微積分相聯系;2)利用導數求函數的單調區間,判斷單調性或根據單調性求參數;3)利用導數求函數的最值(極值),解決生活中的優化問題;4)考查數形結合思想的應用.

例3(2019 年天津卷理20)設函數f(x)＝excosx,g(x)為f(x)的導函數.

(1)求f(x)的單調區間;

(2)當x∈]時,證明:

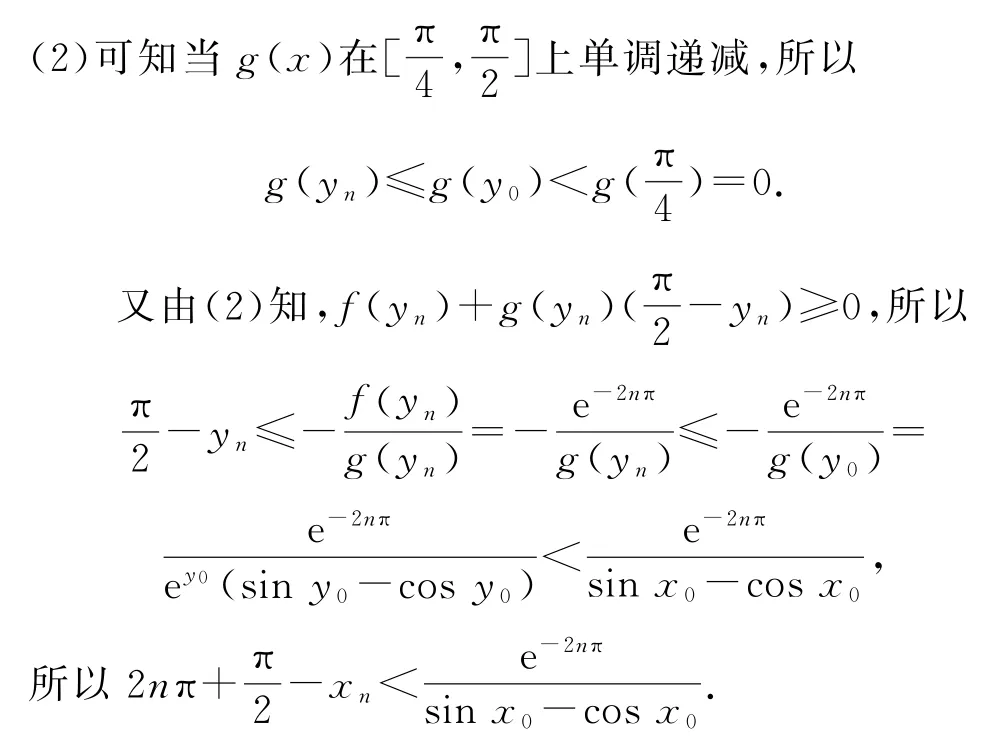
1)利用導數證明不等式或解決不等式恒成立問題關鍵是把不等式變形后構造恰當的函數,然后用導數判斷該函數的單調性或求出最值,以達到證明不等式的目的;2)利用導數解決不等式恒成立問題,應特別注意區間端點是否能取到;3)學會觀察不等式與函數的內在聯系,學會變主元構造函數,再利用導數證明不等式.

3 極值問題

例4(2017年山東卷理20)已知函數f(x)＝x2＋2cosx,g(x)＝ex(cosx－sinx＋2x－2),其中e＝2.71828…是自然對數的底數.

(1)求曲線y＝f(x)在點(π,f(π))處的切線方程;

(2)令h(x)＝g(x)－af(x)(a∈R),討論h(x)的單調性并判斷有無極值,有極值時求出極值.

(1)y＝2πx－π2－2(求解過程略).

(2)由題意可得

則h′(x)＝2(ex－a)(x－sinx),令m(x)＝x－sinx,則m′(x)＝1－cosx≥0,所以m(x)在R 上單調遞增.又因為m(0)＝0,所以當x＞0 時,m(x)＞0,當x＜0時,m(x)＜0.

當a≤0時,ex－a＞0.若x＜0,h′(x)＜0,h(x)單調遞減;若x＞0,h′(x)＞0,h(x)單調遞增,所以當x＝0時,h(x)取得極小值h(0)＝－2a－1.

當a＞0時,由h′(x)＝0,得x1＝lna,x2＝0.

當0＜a＜1時,lna＜0,當x∈(－∞,lna)時,h(x)單調遞增;當x∈(lna,0)時,h(x)單調遞減;當x∈(0,＋∞)時,h(x)單調遞增,所以h(x)極大值為h(lna)＝－a[ln2a－2lna＋sin(lna)＋cos(lna)＋2],極小值為h(0)＝－2a－1.

當a＝1 時,lna＝0,所以h(x)在R 上單調遞增,無極值.

當a＞1時,lna＞0,同理,當x＝0時,h(x)取得極大值h(0)＝－2a－1,h(x)取得極小值h(lna)＝－a[ln2a－2lna＋sin(lna)＋cos(lna)＋2].

此題考查導數的幾何意義、應用導數研究函數的單調性與極值、分類討論思想.恰當分類討論是關鍵,當一次求導不能解決問題時,可以再次求導.易錯點是分類討論不全面、不徹底、不恰當,或對復雜式子變形能力差,從而造成不能完整解答出來.

4 零點問題

對函數零點的考查主要有驗證零點的存在性、判斷零點的個數以及已知零點個數求參數的取值范圍.

例5(2019年全國Ⅰ卷文20)已知函數

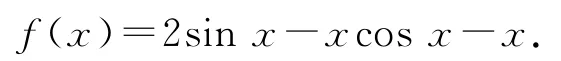
(1)證明:f′(x)在區間(0,π)存在唯一零點;

(2)若x∈[0,π]時,f(x)≥ax,求a的取值范圍.

綜上,f′(x)在區間(0,π)存在唯一零點.

(2)方法1若x∈[0,π]時,f(x)≥ax,令

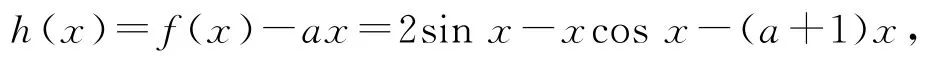
則h′(x)＝cosx＋xsinx－1－a,由(1)可知,

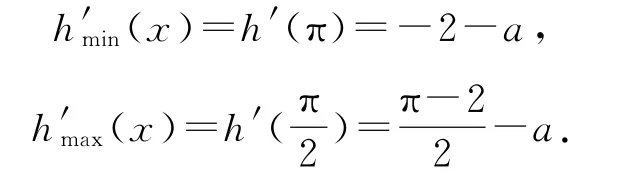
當a≤－2 時,h(x)在[0,π]上單調遞增,所以h(x)≥h(0)＝0,此時f(x)＞ax恒成立.

綜上,a的取值范圍為(－∞,0].

方法2由(1)可知,f′(x)在區間(0,π)存在唯一零點,設為x0,則f(x)在(0,x0)上單調遞增,在(x0,0)上單調遞減.又因為f(0)＝0,f(π)＝0,所以當0≤x≤π時,f(x)≥0,又當a≤0,0≤x≤π 時,ax≤0,故f(x)≥ax;當a＞0 時,f(π)＝0≤aπ,f(x)≥aπ不恒成立.

綜上,a取值范圍為(－∞,0].

本題利用導數討論函數零點個數、根據恒成立的不等式求解參數范圍.對于此類端點值恰為恒成立不等式取等的問題,通法是采用構造函數的方式,將問題轉變成求函數的最值,進而通過導函數的正負來確定所構造函數的單調性,從而得到最值.結合第(1)問的結論分析不等式結構,往往會有出其不意的結果,比如方法2,利用必要性探路,先猜后證,避免了分類討論.我們發現通法中分類討論是通法必不可少的,原因就在于三角函數具有周期性和有界性.

三角函數與指數函數、對數函數、冪函數等綜合的問題,難點在于三角函數求導后依然是三角函數.除了以上幾種類型,還有已知極值點或者零點(個數)求參數取值范圍問題、零點不存在問題、最值問題等.這些題看似是由不同的函數進行融合,但可以利用導數的優越性、三角函數的特殊性對函數的性質進行再次研究,其實最終還是萬變不離其宗,學生做題時要善于提煉方法,進行變式訓練,以提升自身的核心素養.

(完)