談談近年來高考壓軸題中導數綜合應用問題的解決策略
——以解析式中含有ex,lnx 為例

張雪麗

(安徽省蕭城一中)

導數的綜合應用問題是高考的必選題,基本上出現在第20或21題,難度較大,能拉開區分度.這類考題一般圍繞y＝ex,y＝lnx與其他初等函數,綜合考查函數的單調性、最值、零點、極值點、恒成立等,技巧性高、綜合性強,更能充分考查學生的數學抽象、直觀想象、邏輯推理、數學建模等核心素養,彰顯學生思維的靈活性及多樣性.近5年來高考全國卷的14份考卷中有10份涉及ex或lnx函數模型,下面結合幾道典型的高考題說明這類導數綜合應用問題的解決策略.

1 含有ex 的函數模型構造法

例1(2018年全國Ⅱ卷理21)已知函數f(x)＝ex－ax2.

(1)若a＝1,證明:當x≥0時f(x)≥1;

(2)若f(x)在(0,＋∞)只有一個零點,求a.

(1)略.

(2)方法1直接利用原函數模型

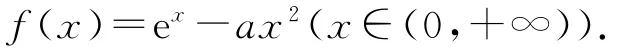
當a≤0時,f(x)＞0恒成立,所以f(x)在(0,＋∞)上無零點.

當a＞0時,f′(x)＝ex－2ax,再次求導可得

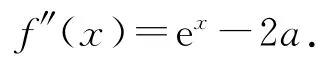
從而 當x∈(0,ln2a)時,f″(x)＜0,當x∈(ln2a,＋∞)時,f″(x)＞0,所以f′(x)在(0,ln2a)上單調遞減,在(ln2a,＋∞)上單調遞增.

當x＝ln2a時,有

當1－ln2a＞0,即a＜時,f′(x)＞0,即f(x)在(0,＋∞)上單調遞增,且f(0)＝1,從而f(x)無零點,所以1－ln2a＜0,f′(ln2a)＜0.

又因為f′(0)＝1＞0,所以存在x0∈(0,ln2a)使f′(x0)＝0,從而當x∈(0,x0)時,f′(x)＞0,當x∈(x0,ln2a)時,f′(x)＜0.又因為＞0,所以存在x1＞ln2a,使f′(x1)＝0,即ex1－2ax1＝0.從而當x∈(x0,x1)時,f′(x)＜0.

當x∈(0,x0)或(x1,＋∞)時,f′(x)＞0,所以函數f(x)在(x0,x1)上單調遞減,在(0,x0),(x1,＋∞)上單調遞增.

然而,端點值f(0)＝1,極小值f(x1)＝ex1－,所以f(x)有唯一的零點x1,即ex1－＝0,結合ex1－2ax1＝0,可以求得x1＝2,a＝.

方法2 構造成“常數＋因式·et”型.

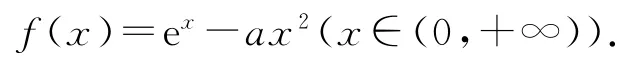
構造函數h(x)＝＝1－ax2e－x(x∈(0,＋∞)).f(x)在(0,＋∞)上只有一個零點?h(x)在(0,＋∞)上只有一個零點,接著研究h(x)＝1－ax2e－x.

當a≤0時,h(x)＞0,h(x)沒有零點.

當a＞0時,h′(x)＝e－xax(x－2).當x∈(0,2)時,h′(x)＜0;當x∈(2,＋∞)時,h′(x)＞0,所以h(x)在(0,2)上單調遞減,在(2,＋∞)上單調遞增,故h(2)＝1－是h(x)在(0,＋∞)上的最小值.

若h(2)＞0,即a＜,則h(x)在(0,＋∞)上沒有零點;若h(2)＝0,即a＝,則h(x)在(0,＋∞)上只有一個零點;若h(2)＜0,即a＞,因為h(0)＝1＞0,所以h(x)在(0,2)上有一個零點.

由(1)知,當x＞0時,ex＞x2,所以

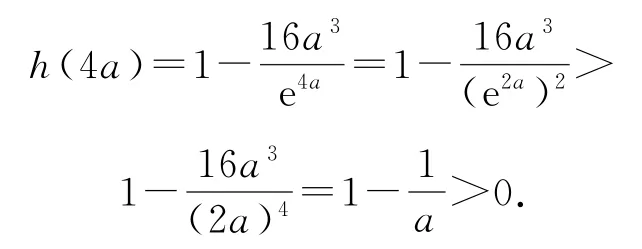
故h(x)在(2,4a)上有一個零點,因此h(x)在(0,＋∞)上有兩個零點.

綜上,f(x)在(0,＋∞)上只有一個零點時,a＝

方法3分離參數構造函數模型

因為f(x)＝ex－ax2在(0,＋∞)上只有一個零點,所以方程ex－ax2＝0在(0,＋∞)上只有一個解,等價于＝a在(0,＋∞)上只有一個根.

含有ex的函數模型常用的構造方法如下,1)直接利用原函數,有時也可分為兩個初等函數模型;2)構造成“常數＋因式·et”型,求導后的運算不易受ex的干擾;3)分離參數法構造函數模型,沒有參數,避免了分類討論,但是有時函數較復雜需多次求導.本題考查了導數與原函數的關系、函數的單調性、零點等知識,涉及函數與方程思想、隱零點問題,考查學生的邏輯推理能力、運算能力、轉化能力、數形結合能力等.

2 含有lnx 的函數模型“獨立與不獨立”法

例2(2017年全國Ⅱ卷21)已知函數f(x)＝ax2－ax－xlnx,且f(x)≥0.

(1)求a;

(2)證明:f(x)存在唯一的極大值點x0,且e－2＜f(x0)＜2－2.

(1)f(x)＝x(ax－a－lnx),因為x∈(0,＋∞),所以f(x)≥0,即ax－a－lnx≥0恒成立.直接構造函數g(x)＝ax－a－lnx,從而

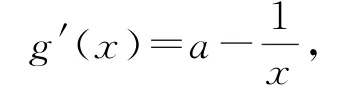
分a≥0,a＜0兩種情況討論,求得a＝1.

(2)利用條件f(x)存在唯一的極大值點x0,一次求導f′(x)＝2x－2－lnx,兩次求導可得

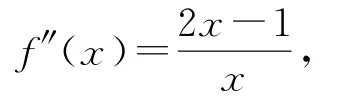
所以函數f′(x)在(0,x1),(x2,＋∞)上單調遞增,在(x1,x2)上單調遞減,所以f(x)的唯一的極大值點為x1.

故f′(x0)＝2x0－2－lnx0,從而

綜上,e－2＜f(x0)＜2－2.

消掉x使lnx的系數為常數,即“獨立”lnx,可一次求導解決單調性問題;當lnx的系數不能消掉時,即lnx“不獨立”,需兩次求導,才能依次推導出單調性、零點、極值點等問題.本題考查了轉化的思想、分類討論的思想,也考查了學生邏輯推理、數學運算、數學建模等核心素養.

變式(2018年全國Ⅲ卷理21)已知函數

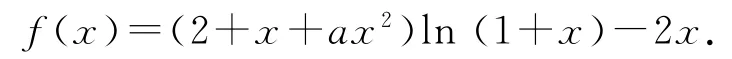
(1)若a＝0,證明:當－1＜x＜0時,f(x)＜0;當x＞0時,f(x)＞0;

(2)若x＝0是f(x)的極大值點,求a.本題解析式復雜,難度較大,仍然可以用例2的兩種方法,獨立lnx一次求導,得到可解的不等式或方程.此方法對于含lnx的函數模型解決如魚得水.

總之,以y＝ex,y＝lnx為載體,融合其他初等函數的導數綜合應用問題,千姿百態、形式不同的表象背后,應歸納研究出解答它們的一般路徑和方法,使后續類似的探究有序可循、思維有法可依,避免學習過程中的盲目性,進而培養學生的整體性思維,這可謂由一棵樹木,看到整片森林.

(完)