導數中的不等式證明策略研究

吳艷麗

(黑龍江省大慶市第二中學)

導數中不等式的證明問題,歷來出現在高考命題的壓軸題中,由于不等式證明方法靈活性很強,因此這類問題具有很高的研究價值.基于此,本文結合具體問題,闡述幾種常見的解題方法,以期拋磚引玉.

1 構造函數法

將不等式的證明問題轉化為函數單調性的應用問題進行求解,這是這類問題最常用的方法,這種方法體現了函數、方程、不等式三者之間的內在聯系.運用這種方法一般分為三個步驟:1)合理構造函數;2)利用導數證明函數的單調性;3)利用函數的單調性證明不等式.

例1若函數f(x)＝1－,點A(1,1)是曲線y＝f(x)與y＝g(x)的公共點,且它們在點A處的兩條切線互相垂直.

(1)求a,b的值;

(2)證明:當x≥1時,f(x)＋g(x)≥

(1)a＝b＝－1(具體求解過程略).

當需要證明的不等式兩邊都含有同一個變量時,我們通常可以直接構造“左減右”的函數,再應用它的導函數來探究它的單調性.

2 放縮法

當所證不等式的不等號中不含等號時,可考慮用放縮法證明,在證明過程中將某部分函數式用另一個函數值比較大(或者比較小)的函數替換,從而構造新的函數,再利用函數的單調性加以證明.

例2已知函數f(x)＝

(1)求函數f(x)的單調區間;

(2)證明:當x＞0時,都有

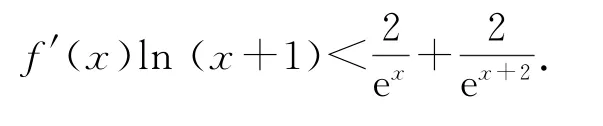
(1)函數f(x)在(0,1)上單調遞增,在(1,＋∞)上單調遞減(求解過程略).

易證lnx≤x－1,當且僅當x＝1時等號成立(證明過程略),所以0＜ln(x＋1)＜x(x＞0).

綜上,當x＞0時,f′(x)ln(x＋1)＜

含有lnx或ex的函數是超越函數,在解決具體問題時應根據這兩類函數的特點及結構特征,對不等式實施靈活變形,并注意重要不等式lnx≤x－1?ex≥x＋1的合理代換.

3 切線法

所謂切線法,就是證明某曲線的圖像恒位于某一點切線處的上方或下方,本質上看就是利用導數研究函數圖像的分布,這種方法體現了數形結合思想.

例3已知函數f(x)＝ex－x2.

(1)求曲線f(x)在x＝1處的切線方程;

(1)曲線f(x)在x＝1處的切線方程為y＝(e－2)x＋1(具體求解過程略).

(2)令g(x)＝f′(x),則g′(x)＝ex－2,當x＜ln2時,g′(x)＜0,當x＞ln2時,g′(x)＞0,故函數f′(x)在(－∞,ln2)上單調遞減,在(ln2,＋∞)上單調遞增.又gmin(x)＝g(ln2)＝f′(ln2)＝2－2ln2＞0,故函數f(x)在(0,＋∞)上單調遞增.由(1)知曲線f(x)在x＝1處的切線是y＝(e－2)x＋1.

又f(1)＝e－1,于是可以猜想函數f(x)的圖像位于切線y＝(e－2)x＋1的上方.

我們先來證明當x＞0時,f(x)≥(e－2)x＋1.

設h(x)＝f(x)－(e－2)x－1(x＞0),則

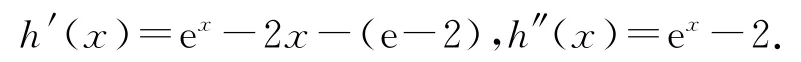
當0＜x＜ln2時,h″(x)＜0,當x＞ln2時,h″(x)＞0,故h′(x)在(0,ln2)上單調遞減,在(ln2,＋∞)上單調遞增.由h′(0)＝3－e＞0,h′(1)＝0,0＜ln2＜1,則h′(ln2)＜0,故存在x0∈(0,ln2),使得h′(x0)＝0,故當x∈(0,x0)∪(1,＋∞)時,h′(x)＞0,當x∈(x0,1)時,h′(x)＜0,故h(x)在(0,x0)和(1,＋∞)上單調遞增,在(x0,1)上單調遞減.

又因為h(0)＝h(1)＝0,故h(x)≥0,即f(x)≥(e－2)x＋1,當且僅當x＝1時等號成立,故當x＞0時,ex－x2≥(e－2)x＋1,即≥x,又因為x≥lnx＋1,當且僅當x＝1時等號成立(證明過程略),所以≥lnx＋1,當且僅當x＝1時等號成立.

利用切線法證明這類不等式時,往往還要用到放縮法,這種方法靈活性強.當然這種方法的出現往往不是憑空產生的,當問題的第(1)問要求我們求曲線在某一點處的切線方程時,我們往往要考慮能否運用切線放縮法來證明不等式.

4 應用函數的凹凸性

在不等式恒成立問題中,有些試題往往以曲線與切線靜態或者動態的位置關系為幾何背景,這時我們可以著眼于曲線的凹凸性,從而獲得清晰自然的思路.

例4已知函數f(x)＝(x＋1)lnx,曲線y＝f(x)在x＝1處的切線方程為y＝ax＋b.

(1)求證:x＞1時,f(x)＞ax＋b;

(1)當x＞1 時,f(x)＞2(x－1)(證明過程略).

(2)由(1)知當x＞1時,有(x＋1)lnx＞2(x－1).令x＝n2－2＞1(n≥2,n∈N*),則

本題中f(x)的一階導函數為f′(x)＝lnx＋二階導函數為f″(x)＝＞0,這說明原函數f(x)是凹函數,故不等式(x＋1)lnx＞2(x－1)恒成立.

導數中不等式的證明問題是一個永恒的話題,也是一個永遠值得研究的課題,這類問題的解決沒有相對固定的思路與方法,面對具體問題,我們必須從問題的實際情況出發制訂解題方案.因此解答這類問題不可故步自封,不可按部就班,應大開腦洞,打破常規,不斷探索,善于從數學的基本思想與方法的角度去分析問題,才有可能找到解決這類不等式證明問題的最佳思路與方法.

(完)