基于穩定圖分組加權的最優模態參數自動識別算法研究

焦恒昌

（中國電子科技集團公司第二十二研究所，山東青島，266100）

結構模態參數用于表征結構的固有動態特性，試驗模態分析主要通過控制系統激勵，對結構系統的輸入時域信號和輸出時域信號進行同步測量，通過時域或者頻域的數學算法處理得到系統頻響函數(頻域)或者傳遞函數(時域)，利用曲線擬合等方法識別出系統的頻率、阻尼和振型[1]。多參考點最小二乘復頻域法（PRLSCF）是國際近年發展并流行的基于系統傳遞函數的模態分析方法，該方法對系統模態的頻率、阻尼和振型都有很好的識別精度[2]。而在實際的工程應用中，輸入輸出信號的測量、傳輸中會有環境噪聲的影響，得到的數據質量是有區別的，數據的有效性也參差不齊。一方面多參考點最小二乘復頻域法處理過程中對不同質量數據做了同等對待，影響模態識別精度；另一方面，目前人工手段借用穩定圖進行的模態參數識別，對操作者個人素質要求較高，影響方法便捷應用。

本文針對PRLSCF算法中對不同質量數據缺少有針對的區別合理對待利用，以及人工拾取穩定圖中物理模態自動化程度低，研究了基于穩定圖分組加權的最優模態參數自動識別算法。

1 理論分析

1.1 加權綜合頻響函數

PRLSCF算法模態參數識別技術利用系統輸入輸出得到多個頻響函數,構造頻響函數矩陣。在頻域中，系統輸出和輸入的關系可用右矩陣分式模型（RΜFD）來描述[2]，右矩陣分式模型的表達式為：

且Uo(ω)和D(ω)可以表示成如下形式：

式中：N—多項式階次

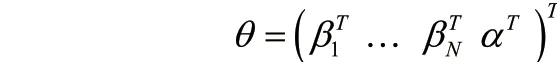
其中:

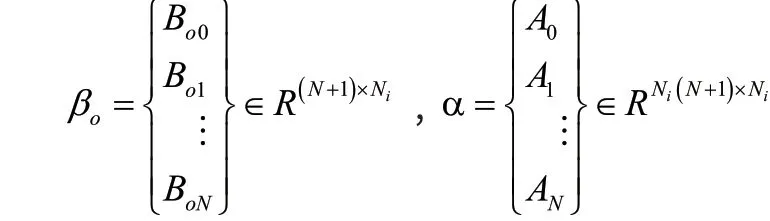
對于參數矩陣θ做非線性最小二乘（NLS）目標函數為：

式中：?H：矩陣的復共扼轉置；

tr(?)：矩陣的跡，即矩陣的主對角元素之和。

利用數學方法求上式極小值，便得到θ矩陣的估計值。

因此通過試驗測量輸入輸出數據數據質量高低，直接影響結構系統測量頻響函數逼近真實系統頻響函數程度，進而對最終模態參數識別精度產生直接影響。

定義加權綜合頻響函數：

其中：

加權綜合頻響函數不再是多次試驗結果頻響函數的簡單平均，而是充分考慮每次試驗的頻響函數質量，即每次輸入與輸出的相干函數作為加權函數，當頻響函數質量較高則在加權頻響函數中具有較高的權值，頻響函數數據質量劣質時則在加權函數中權值較低。這樣即達到提高優質數據在計算過程中的權重，提高模態參數識別精度。

1.2 基于穩定圖分組加權的最優模態參數自動提取

在模態分析中，穩定圖是分離結構物理極點和數學極點（虛假極點）的有力工具[3]。穩定圖的建立方式為：坐標軸橫坐標為頻率，單位Hz，坐標軸縱坐標為的階次值，圖上標注特定文字符號。由于利用穩定圖模態識別需要對模型階次假設，且假設階次要高于系統固有階次，通過計算得到物理模態及計算虛假模態。但是一般實際情況是隨模型假設階次遞增，物理模態作為真實模態，始終保持穩定在一條軸上；而通過計算出現虛假模態則隨機離散出現，散布于穩定圖上，不會出現類似于真實模態穩定軸。根據結構系統這個性質，便比較直觀在穩定圖上區別開物理模態和虛假模態。根據工程經驗，系統假設的階次取值越大，在穩態圖上反映的極點信息越全面，防止出現漏掉的穩定極點，也便于出現穩定軸；但是階次估值提高也帶入了許多虛假的極點信息，這樣會給極點分離帶來困難。這就要需要權衡估計階次高低的優劣，選取合適估計階次。

穩定圖上不同估計階次情況下極點分布，在同一模態軸上，相鄰階次模態參數相比較，若相鄰階次模態參數差值不高于容差設定值，則該極點為穩定極點，得到的模態參數為穩定模態參數。假定特征頻率容差為f? ，阻尼比容差為 ξ?，則穩定點的條件為：

其中j表示系統模型階數，f、ξ表示不同估值階次下的模態頻率、阻尼比。

通過專家人工對模態極點篩選的步驟，可將模態識別過程劃分為：首先選擇理想的極點列，然后在列中選擇比較好的極點，進而對系統進行模態參數識別。因而進行自動化模態參數識別的基礎是按照專家篩選過程對每一步的標準進行量化。主要分為以下幾個步驟：

①基于加權的最優極點列提取

根據不同模態參數識別方法，假定不同模型固有階次，得到的所有計算極點（即虛假極點）將散布于整個穩定圖上。系統固有模態并不會隨著模型階次的提高而大的改變，而計算的虛假模態則會隨著模型階次提高而變化較大。

在整個需要分析頻帶內分成若干頻帶組，一般是每組帶寬為整個分析頻帶的0.5%~1.0%，若是模態更為密集，則可根據具體情況相應提高分組組數，得到標準組列。但存在邊界與固有頻率重合情況，利用標準分組再偏移半個標準組帶寬得到新的偏移組列，統稱為極點列，如圖1所示。

圖1 穩定圖頻帶組分組示意圖

將每個標準組列及偏移組列中的極點通過加權計算該組總分值，其中“s”類權分ws，“d”類權分wd，“v”類權分wv，“f”類權分wf，得到每一組的極點列加權分值：

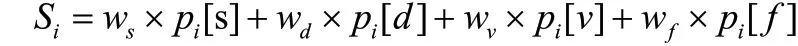
根據最終加權分值的大小，得到前N個基于加權的最優極點列 {Si}。

②加權最優極點簇選擇

得到最優極點列后，需要選擇最優極點列 }{iS中的最優極點作為模態極點。但是極點列中有很多極點，為了減少虛擬極點混入，首先將每極點列分成若干極點簇，選擇最優極點簇，整個流程如圖2所示。

圖2 加權最優極點極點簇選擇流程圖

③最優穩定極點選擇

在最優極點簇選擇平均阻尼比相差最小的極點作為最優穩定點。

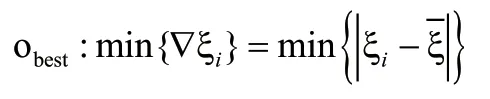
因此，整個基于穩定圖分組加權的最優結構模態參數自動提取過程為：首先根據多次測量的數數輸出采集數據計算實測頻響函數矩陣，利用相干函數作為加權函數構造加權的綜合頻響函數矩陣，然后根據實際分析頻帶設定出最高假定階次，利用多參考最小二乘復頻域法構造穩定圖，最后利用基于穩定圖分組加權自動拾取最優穩定極點，對系統模態參數進行計算。整個過程流程圖如圖3所示。

圖3 基于穩定圖分組加權的最優模態參數自動提取流程圖

2 實驗論證與分析

為了驗證方法的有效性，以一個三自由度線性時不變系統作為仿真結構[4]，如圖4所示。

圖4 三自由度線性時不變振動系統

表1 系統的頻率和阻尼比理論值

對系統中m1激勵，激勵類型為脈沖激勵，力大小f1=1kN，同步對3個質量塊時域位移響應信號采集，設置采樣頻率40Hz，采樣時長150s。得到各點位移響應如圖5所示。由圖5看出各測點位移響應已經得到很好的衰減，不需要加窗函數處理。

圖5 三自由度系統位移響應時域圖

對輸入輸出響應分別加1%，5%，10%的隨機噪聲作為模擬三次采樣數據，并根據輸入輸出并做頻率響應函數，以m1為例如圖6所示。

圖6 m1不同噪聲下頻響函數曲線

對不同加噪處理后的輸入輸出信號處理，分別計算系統頻響函數矩陣和相干函數矩陣，進而可計算平均頻響函數和本文方法的加權綜合頻響函數。利用以上數據對系統分別采用PRLSCF和改進PRLSCF進行模態分析，假設模型最高階數為64，分別得到系統穩定圖如圖7、圖8所示。

結合圖7和表1看出，穩定圖上在系統固有頻率處出現了由穩定點（s）所構成的清晰穩定軸，但在非固有頻率出也出現了穩定軸，即計算出的虛假穩定軸。因此這些虛假穩定軸在模態拾取就會被誤拾取，計算出多余錯誤的模態識別結果。在圖7，圖8穩定圖中虛假穩定極點明顯減少，在系統固有頻率處的穩定軸更加明顯清晰，使得拾取穩定軸變得更加容易，模態參數識別可操作性更強，減少結構系統模態參數識別中誤判率。

圖7 PRLSCF方法構造的穩定圖

圖8 改進PRLSCF方法構造的穩定圖

最后基于穩定圖分組加權的最優結構模態參數自動提取識別結果如表2所示。可以看出，多參考最小二乘復頻域法和本文的方法都可以得到系統的三階固有模態參數，但是在阻尼比和固有頻率識別的精度上，本文方法比原有的多參考最小二乘復頻域法誤差更小，更接近于理論值。

表2 兩種方法識別結果對比

3 結束語

對現有PRLSCF模態參數識別算法進行優化并提出基于穩定圖分組加權的最優結構模態自動識別算法。對PRLSCF模態識別算法進行優化，提出加權的多參考最小二乘復頻域法模態參數識別，以輸入輸出相干函數為加權函數得到綜合頻響函數，通過增加高質量采集數據的權重，更加有效利用高質量采集數據，提高系統模態參數識別精度；提出了基于穩定圖分組加權的最優結構模態參數自動識別，根據穩定圖中計算模態的頻率、阻尼比等分組加權，自動拾取最優物理極點并進行模態參數計算，提高了模態分析自動化程度。最后通過仿真的三階物理模型進行系統模態參數識別，本文方法比原PRLSCF法構造出的穩定圖更加清晰，可實現自動識別模態參數，驗證了本文方法的可行性與正確性。