Increasing the efficiency of post-selection in direct measurement of the quantum wave function

Yong-Li Wen(溫永立) Shanchao Zhang(張善超) Hui Yan(顏輝) and Shi-Liang Zhu(朱詩亮)

1National Laboratory of Solid State Microstructures and School of Physics,Nanjing University,Nanjing 210093,China

2Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials,School of Physics and Telecommunication Engineering,South China Normal University,Guangzhou 510006,China

3Guangdong-Hong Kong Joint Laboratory of Quantum Matter,Frontier Research Institute for Physics,South China Normal University,Guangzhou 510006,China

Keywords: weak measurement,quantum state

1. Introduction

A wave function is a fundamental concept in quantum mechanics,[1,2]and its determination is therefore of crucial importance in many applications. However, with the traditional quantum measurement methods developed by Von Neumann,[1]we can only obtain the modulus square of the wave function,which determines the probabilities of all kinds of measurement outcomes. For a long time, quantum-state tomography has been considered as an operational measurement method to reconstruct the wave function.[3-7]Quantumstate tomography is a conventional way to construct a quantum wave function,but it usually requires plenty of projection measurements on several bases sets,and thus it is also considered as an indirect measurement method with a limitation in efficiency and concision.

Recently, an alternative method of measuring the wave function was proposed in Ref. [8] based on the concepts of weak measurement[9-21]and post-selection. This method was named “direct measurement” in Refs. [8,22]. The word “direct”here expresses that the real and imaginary components of the wave-function are proportional to the signal of the experimental apparatus and no complicated computation is required.

The method has been widely applied for measurement of quantum states.[23-33]The method has also been generalized from the weak measurement to the strong measurement.[34-38]On the other hand,an alternative direct measurement strategy based on aδ-quench probe was developed:quenching its complex probability amplitude one by one (δquench) in a given basis,one can directly obtain the quantum wave function of a pure ensemble by projecting the quenched state onto a postselection state.[39,40]However, the efficiency of these direct measurement methods is limited by the success probability of post-selection,[41]which is usually pretty low in a practical experiment, and thus increasing the efficiency of post-selection is highly needed.

Analyzing carefully the measurement efficiency of the experiment in which the transverse wave function of a photon was measured with the direct measurement method,[8]we find that the efficiency is mainly dependent on the success probability of post-selection. In this article, we propose a modified method that can significantly increase the efficiency of directly measuring photon’s wavefunction by inserting a polarization dependent Fourier transformation(Pol-FT)lens before post-selection stage. In the previous direct measurement scheme,[8,34]the photons would be post-selected to a zero transverse momentum state, but the distribution in zero momentum is pretty low,especially under the conditions of high resolution and high measurement fidelity.With a liquid crystal plate as the Pol-FT lens,almost all the input photons can contribute to the zero momentum components in post-selection stage. Therefore, the post-selection would not decrease the measurement efficiency. Numerical simulations demonstrate that our proposal can have greater efficiency in higher resolution and higher fidelity. Our modified method can thus greatly increase the measurement efficiency of the direct measurement of the quantum wave function.

This paper is organized as follows. In Section 2, we review a general method of direct measurement of the wave function, including the previous weak and strong measurements as examples. The efficiency of the method is discussed.In Section 3, we propose a modified method to improve the efficiency of post-selection. Section 4 investigates the performances of our proposed method. Finally,short discussion and conclusion are given in Section 5.

2. Direct measurement of the wave function

In this section, we present a general direct measurement method which includes the case under a weak coupling proposed in Ref. [8] and strong coupling proposed in Ref. [34],and then discuss the efficiency of this method.

We consider to measure a quantum wave function|ψ〉=∑x ψ(x)|x〉,where the basis{|x〉}are position eigenstates of a discretized segment. A measurement can be considered as the coupling between an apparatus and a physical system that results in the translation of a pointer. Here we study the case of a photon spatial wave function, and the pointer can be represented by the polarization of the photons. The coupling between an observable and the pointer can be written as a Hamiltonian ?H=g?πx?σy,where ?πx=|x〉〈x|,gis the coupling strength, and ?σx,y,zin this paper represent the Pauli matrices.The evolution operator with arbitrary coupling strength can be written as

Benefit from the higher coupling strength, this direct strong measurement method has better precision in wave function measurement. We will focus on the strong coupling case in this paper.

The prefactorsβφ*pof the wave functionψ(x)in Eq.(7)determine the efficiency of the direct measurement,which averagely describes the magnitude of input photon energy that can contribute to the final detectable signal. In the experiment reported in Ref. [8],φ*pis the probability amplitude at zero momentum of the initial state|ψ〉. Thus|φ*p|2is the success probability of projecting|ψ〉to the post-selection state|p0〉.βis the inner product of a momentum eigenstate and a position eigenstate,and its square modulus|β|2=|〈p0|x〉|2is the probability of|x〉to be in|p0〉. Strictly speaking, the momentum uncertainty of a position eigenstate is infinite, so|β|2approaches to zero. However, in a real experiment, both|p0〉and|x〉have widths which are relative to their measuring steps. Therefore,|β|2is practically a small value instead of zero. The greater the prefactor|βφ*p|,the higher signal intensity in the measurement,which leads to a higher signal-tonoise ratio. Because|φ*p|is determined by the unknown state|ψ〉,it is unable to increase without the knowledge of this initial state. Butβis independent from|ψ〉, so it is able to be modified. Therefore, optimizing the value of|β| plays a key role in improving the efficiency of a direct measurement experiment.

3. Proposal to improve the probability of postselection

As a concrete example, we address our method to optimize the efficiency of post-selection based on a previous optical experiment,[8]which is schematically shown in Fig.1. In the experiment,the researchers considered a photon travelling along thezdirection,and the aim is to directly measure thexwave function of the photons.

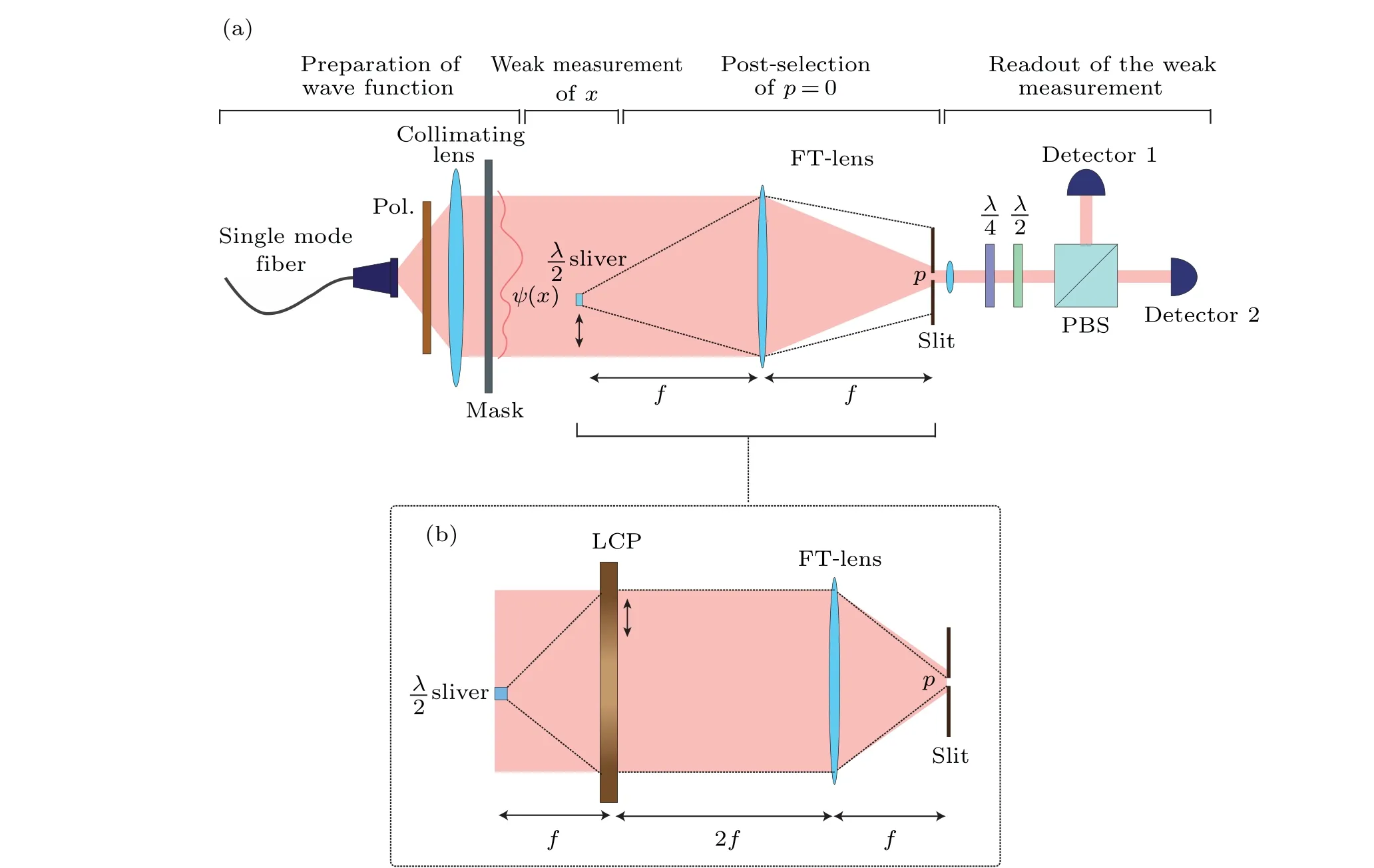
Fig.1. (a)Schematic setup of the experiment proposed in Ref.[8]to directly measure the quantum wave function. The experiment has four sequential steps: state preparation,interaction of the probe system and the pointer,post-selection of the system,and readout the measurement results. (b)Our modified method to increase the efficiency of the post-seletion.

An ensemble of single photons are emitted from a single mode fiber and collimated. The polarization of the photons is chosen as the pointer in the measurement. The polarizer(Pol.) is used to initialize the polarization state of the photons to be|0〉. The photons pass through a collimating lens to make the transverse mode of the photons a nearly parallel propagating Gaussian beam. A phase mask placing after the collimating lens generates the initial quantum wave functionψ(x). A half-wave plate(λ/2)sliver placing at the transverse positionxperforms the coupling between the pointer and the wave functionψ(x). We can consider that the photons have been divided into two parts: the unperturbed part in the pointer state|0〉,and the signal part in the pointer state|1〉. As Eq. (3) shows, the signal part is carrying the information of the wave functionψ(x). In the previous direct measurement scheme,[8,34]the photons would be post-selected to the transverse momentum state|p=0〉after the coupling. The dashed line in Fig.1(a)shows the propagation of the signal part. The photons modulated by theλ/2 sliver evolve approximately like a point-source light. Then the Fourier transformation lens(FT-lens)transforms the light to a momentum spectrum at the focal plane. As the measuring regionδxis small, the uncertainty of the transverse momentum of the signal part is very large compared with the post-selected momentump ≈0. It leads to a consequence that only a small portion of the signal part can be successfully selected by the slit. Thus it largely limits the efficiency of the measurement.

After the slit, a lens is used to collimate the outcoming light. Then the quarter-wave plate (QWP), half-wave plate(HWP)and the PBS are used to project the final pointer state to four diagonal bases respectively. This step is to read out the expectation valuesP±,PL,R,andP1in Eq.(7).

whereλis the wavelength of the photon andcis the velocity of light(see Appendix A).The transverse center of LCP is aligned with theλ/2 sliver. We denote the transverse position at the LCP asx′. Thus we can use a unitary operator to describe the evolution of the photon,

4. Performances of the improved method

Fig. 2. (a). The factor |β| as a function of x. δ p can be chosen in[0,π/L],where[-L,L]is the measuring range of ψ(x)in x. The function|β|of each curves has been normalized in the measuring range.

In a practical experiment,|p0〉is not an exact zero momentum state, it should be an integral of momentum eigen states in the range [-δ p,δ p].δ pis related to the width of the slit which can be expressed asδ p=πlslit/fλ. Under this condition,βcan be recast as

We calculate the fidelityFas a function ofδ pfor various waistsa, and the results are shown in Fig. 3. The range ofδ pis[0,π/L],and the measuring positionx ∈[-L,L]. These two ranges satisfy the condition of 2π/(2L)=π/L, which is required for the discrete Fourier transformation. It is clearly that the fidelity decreases with increasingδ p.

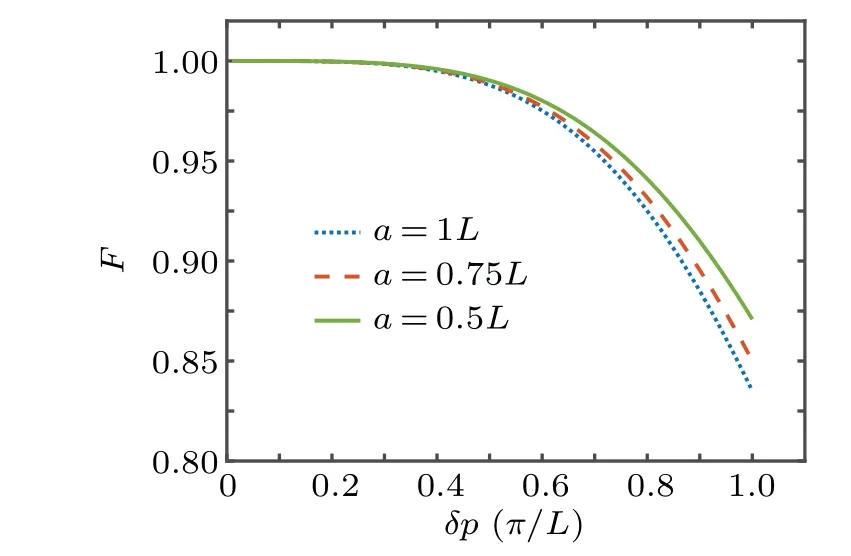
Fig. 3. The fidelity F of the measured wave function as a function of δ p. The waists of the Gaussian wave packets a=1.00L,0.75L,0.50L.

On the other hand,the width of the measuring stepδxalso affectsβ.δxcan be considered as the uncertainty of transverse position. According to Heisenberg’s uncertainty principle,the uncertainty of transverse momentum becomes larger whenδxdecreases. For a givenδ p, higher resolution of the measurement will lead to a lower efficiency of post-selection.

For a fixedδxandδ p,βcan be written as a double integral formulation

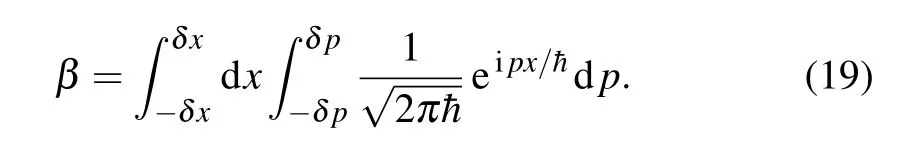
Figure 4 shows the magnification factorM=1/|β|as a function of numberNwhich is the measuring points with a given measuring rangex ∈[-L,L]. The magnification factor is higher when the numberNincreases. Furthermore, our proposed method has a higher efficiency for higher resolution and fidelity.

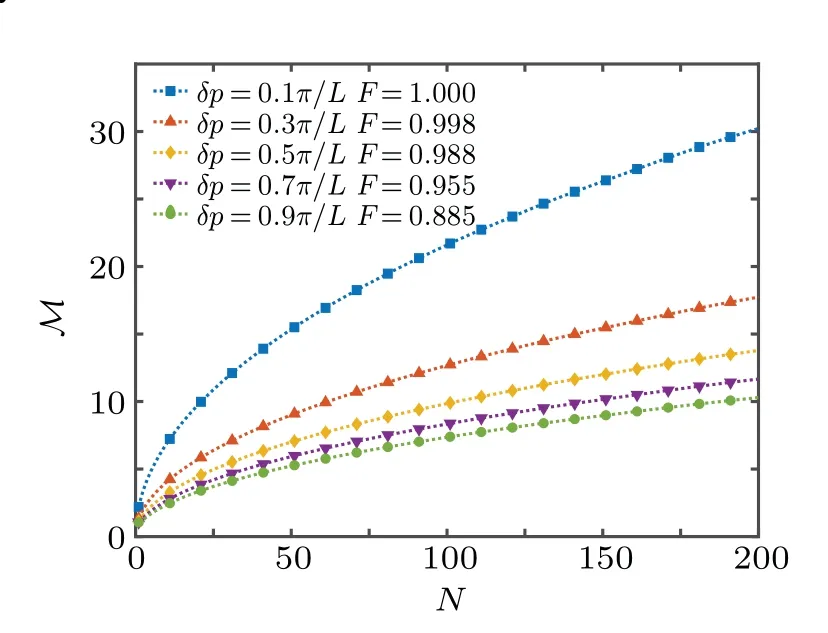
Fig.4. (a). The magnification factor M as a function of the measuring point N. The waist of the Gaussian wave packet a=L.

5. Discussion and conclusion

We now discuss the improvement of the efficiency under the conditions in Ref. [8], where the parametersL=30 mm,δx=1 mm,f=1000 mm,lslit=15 μm, andλ=800 nm.We can estimate the width of measuring stepδx ≈0.033Land the post-selectionδ p ≈0.563(π/L)by using the formulaδ p=πlslit/fλ. With these two parameters (δxandδ p), we can obtain|β|≈0.138 by numerical calculation. Therefore,if we modify the experimental setup in Ref.[8]with our proposal,it would have a magnification ofM=1/|β|≈7.24 in efficiency increasing.

In summary,we have proposed a modified scheme to directly measure the quantum wave function by simply adding a LCP after the coupling between the pointer and the wave function. Our modified method can significantly increase the efficiency of post selection. Numerical simulations have shown that our proposal can have a greater efficiency in higher resolution and fidelity.

Acknowledgments

This work was supported by the Key-Area Research and Development Program of Guangdong Province, China(Grant No. 2019B030330001), the National Natural Science Foundation of China (Grant Nos. 12074180, 11804105,U20A2074, and U1801661), the Key Project of Science and Technology of Guangzhou (Grant No. 2019050001),the National Key Research and Development Program of China (Grant No. 2020YFA0309500), and the Natural Science Foundation of Guangdong Province, China (Grant No.2018A0303130066).