Probabilistic resumable quantum teleportation in high dimensions

Xiang Chen(陳想) Jin-Hua Zhang(張晉華) and Fu-Lin Zhang(張福林)

1Department of Physics,School of Science,Tianjin University,Tianjin 300072,China

2Department of Physics,Xinzhou Teacher’s University,Xinzhou 034000,China

3School of Mathematical Sciences,Capital Normal University,Beijing 100048,China

Keywords: probabilistic teleportation,entanglement,successful probability

1. Introduction

Quantum teleportation is one of the processes unique to the quantum information, which serves as an important example for the most intriguing uses of entanglement.[1-4]It has been widely studied both theoretically and experimentally since it was put forwards.[5-24]One reason for it gains so much attraction is that, the original scheme and its various extensions play key roles in several contexts in quantum communication,including quantum repeaters,quantum networks and cryptographic conferences.[25-29]

In the original and also the simplest version of teleportation,[2]Alice (the sender) can transfer an unknown state from a qubit to Bob (the receiver), with fidelity 1 and successful probability 1,without physical transmission of the qubit itself. The key ingredient in the protocol is a two-qubit Bell state shared by them as a quantum channel. Alice makes a joint measurement on the two qubits in her hands,projecting them onto one of the four Bell states with equal probability.Through a classical channel, Alice sends Bob two classical bits to inform him of her outcome. According to the classical information, Bob can perform appropriate unitary operations on his qubit to rebuild Alice’s initial state,and thereby accomplishes the teleportation.

A variant of the process called probabilistic teleportation was proposed based on the consideration that a quantum channel may be prepared in a partially entangled pure state in practice.[5-9]Such teleportation is exact (with fidelity 1),but may sometimes fail as the price to pay for the fidelity. In principle, Alice’s joint measurement is destructive, and it is generally assumed that the information encoded in the state to be teleported is lost when the teleportation fails. In their recent work,[9]Roa and Groiseau presented a nondestructive scheme for probabilistic teleportation by introducing an ancillary qubit. This avoids losing the initial information and offers the chance to repeat the teleportion process. The nondestructive scheme has been extended in many branches, including bidirectional teleportation,[30]teleportation of an entangled state[31]and multihop scenario.[32,33]

In this work, we present a general protocol for nondestructive probabilistic teleportation of high-dimensional quantum states,in which Alice can resume her initial state when the teleportation fails. The motivation for this work is not only to extend the study of Roa and Groiseau to high-dimensional systems, but also based on the following considerations. In theory,high-dimensional channels,especially the partially entangled ones, have more rich entanglement properties. Our protocol provides a sample to study the cooperative relationship among the entanglement, joint measurement and classical information in a quantum information process. In practice,teleporting high-dimensional states is required in the task to completely rebuild the quantum states of a real particle remotely.And, recent experiment progresses[16,17]show the possibility of implementing our present protocol in optical systems. We make a remark here that,although Fuet al.[32,33]give a version of nondestructive probabilistic teleportation in high dimension using an auxiliary particle in Bob’s hand,we maintain the approach in Ref. [9] with an ancilla belonging to Alice. In this case, only the sender, Alice, is required to have the ability of bipartite operations, such as generation and measurement of entangled states.

In addition, one can notice the similarity of our protocol and the quantum two-path interference experiments.[34]In the latter,interference fringes vanish when the which-path information is acquired by a detector, while reappear when the detector returns the information to the particle. The ancilla in our protocol can be regarded as a quantum apparatus to measure Alice’s system. The initial state is recovered by erasing the information recorded after an unambiguous quantum state discrimination.

2. Teleportation of a qutrit

Let us start with the teleportation of a qutrit(a three-level quantum system). Suppose Alice wishes to teleport to Bob an arbitrary qutrit state as

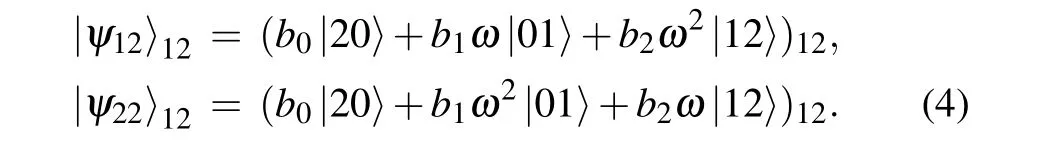
The vector of qutrit 3 in each term (each line) of the total state (3) is equivalent to the initial state (1) under a unitary transformation. However,the corresponding states of qutrits 1 and 2|ψnm〉12are not orthogonal to each other. To teleportate the initial state exactly,an option is that,Alice performs an unambiguous quantum state discrimination process,[6,7,12,13]to distinguish the nine states with no error but a probability of failures. As in the standard teleportation through a maximal entangled quantum channel,[16,17]Bob can rebuild the initial state on his qutrit by performing appropriate unitary operations according to Alice’s outcome. In another scheme, Alice still performs a joint measurement in nine maximally entangled basis, while Bob needs an extracting quantum state process.[5]Here, we follow the former scheme, which only requires Alice’s ability to manipulate two or more particles.

Fig. 1. Alice’s sequential operations on her subsystems: (1) The GCNOT gate C21 factorizes the states of 1 and 2 to be discriminated. (2)The apparatus 0 measures 1 by using C?10. (3) Alice performs a joint transformation D21 on 1 and 2 to discriminate the states of 2. (4) The GCNOT gate C10 erases the information of 1 recorded in 0. (5) Alice measures 0 to divide the procedure into success and failure parts.

For the sake of brevity, before putting forward our final total state in this section, we only show the states in the hands of Alice. We show the sequential operations of Alice in Fig.1. To discriminate the nine two-qutrit states(4),Alice factorizes the states by applying a generalized controlled-NOT(GCNOT)gate onto her bipartite system and obtain

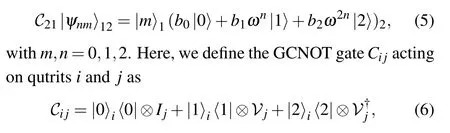
whereIjis the identity ofjandVj=|0〉j〈1|+|1〉j〈2|+|2〉j〈0|. It shifts the targetjclockwise or anticlockwise when the control qutritiis a|1〉or|2〉.

To distinct the nine states in Eq. (5), Alice can perform a von Neumann measurement on qutrit 1 followed by an unambiguous quantum state discrimination on qutrit 2.However,these operations destroy the initial state of qutrit 1 even though the discrimination fails. Here, following the protocol of Roa and Groiseau,[9]we introduce an extra auxiliary qutrit 0 which acts as a quantum apparatus to measure qutrit 1. The key point is that, when we erase the information of qutrit 1 recorded in the ancilla,the initial state of qutrit 1 recoveries when discrimination fails. Alice applies the inverse of the GCNOT gate on the ancilla initial in|0〉0and qutrit 1,and obtain the nine states in her hands as

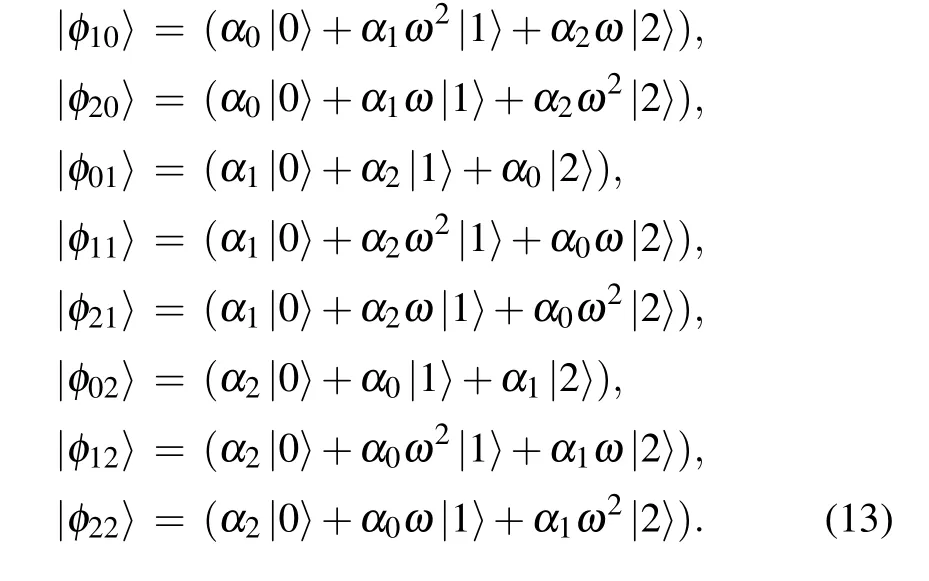
Then, the state to be teleported is encoded in qutrit 3 in the first part of|Δ〉,but in qutrit 1 in the second part.

Alice performs a von Neumann measurements on qutrit 0 in the standard basis.It projects qutrit 0 to|0〉0in a probability 3|b0|2. Then,she measures the nine orthogonal direct product states|0〉0|m〉1, and informs Bob to perform appropriate unitary operations on his qutrit 3 to rebuild the initial state, and thereby the teleportation succeeds. On the contrary,the qutrit 0 could be projected to|1〉0in a probability 1-3|b0|2,which means the failure of the teleportation. Alice can recover the state|φ〉1in qutrit 1, by performing a joint unitary transformation?21=I1?(|0〉2〈0|+|2〉2〈2|)+V1?|1〉2〈1|on qutrits 1 and 2. Alternatively, Alice could perform a von Neumann measurements on qutrit 2 in the standard basis.She obtains the initial state|φ〉1, by using the operationV1on qutrit 1 when qutrit 2 was projected to|2〉2, whileI1corresponding to|0〉2and|1〉2.

3. General protocol

Now we turn to the general protocol for teleporting a quNit (aN-level quantum system) through a partially entangled two-quNit quantum channel. Since it is direct to extend the above scheme toN-level systems,we present the following results in compact general formulae in this part. Let an initial quNit state to be

4. Summary

We present a scheme for nondestructive probabilistic teleportation of high-dimensional quantum states.A partial entangled pure state severs as the quantum channel, whose smallest coefficient determines the successful probability of exactly teleporting a state. With the aid of an auxiliary particle,Alice can recover her initial state to be teleported when teleportation fails. Compared to the existing results,[32,33]our protocol only requires the sender,Alice,to have the ability to perform bipartite operations,while the dimension of the ancilla needs to be the same as the state to be teleported. In addition, the ancilla acts as a quantum apparatus to measure Alice’s system. The process of resuming the initial state can be regarded as erasing information recorded in the ancilla.

As the following research, it is a fundamental problem to explore the roles of quantum correlations in our four-party procedure, which is a fundamental problem in quantum information. In addition, the relation between our protocol and the theory of extracting information from a quantum system by multiple observers[35]would be interesting,since the quantum correlations in the latter are studied in many works.[36-38]While we focus here on the teleportation using quantum channels with the same dimension as the state to be teleported,it is a natural extension to apply the present ideas in the case with different dimension.[14]And finally,we hope that the process can be implemented in laboratories with the help of the techniques recently developed in optical systems.[16,17]

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 11675119 and 11575125)and Shanxi Education Department Fund, China (Grant No.2020L0543).