基于圖論的無人機傳動系統構型設計

王向勝，林文琦，韓璇璇，袁毓雯，宋文錦

基于圖論的無人機傳動系統構型設計

王向勝，林文琦，韓璇璇，袁毓雯，宋文錦

（西北機電工程研究所，陜西 咸陽 712099）

傳動系統作為無人機的核心系統，一定程度上決定了無人機的性能。針對傳統傳動系統設計效率低下的問題，本文提出基于圖論的傳動系統構型設計方法。首先，介紹傳動系統圖論表示、網絡流、最小費用網絡流等圖論相關理論；其次，提出一種針對無人機傳動系統的功率流建模方法，建立數字化模型，通過計算機自動化傳動比分配，進行功率流分析，得到最優的傳動系統構型方案；最后，以單發動機雙旋翼傳動系統為例，利用本文提出的最小費用網絡流分析方法對傳動系統進行構型分析，從而檢驗所提出方法的合理性和采用約束條件的正確性，為后續無人機傳動系統的計算機自動化設計建立基礎。

傳動系統構型；圖論；無人機；功率流

無人機因結構緊湊、垂直起降、能在空中懸停、機動性高和野外適應環境能力強等優勢，被廣泛應用于情報偵察、環境監視、通信中繼、電子干擾與對抗等軍事和民用方面。傳動系統作為無人機的重要組成部件，其性能的優劣在一定程度上決定了飛行器的綜合性能。

在傳動系統的開發過程中，構型設計是傳動系統的初始階段，其任務是根據設計技術要求設計傳動總體方案，并擬定出符合設計要求的初步設計方案；經論證篩選之后進一步確定傳動系統結構方案。傳動系統構型設計和評估，作為傳動系統總體設計的頂層思維和方案設計內容之一，旨在協調功能（運動、動力的傳遞）和形式（傳動件空間結構、傳動件空間布局或分布）兩者相互影響、相互制約且不可分割的和諧、統一關系。傳統的傳動系統設計方法存在效率緩慢、費時費力、易被人為干擾等問題。

隨著計算機技術的發展，為避免人為因素對傳動方案選擇造成的局限性，構型的計算機自動生成技術得到越來越多關注。E. Pennestri等[1]對差動輪系進行基于圖論的功率流和靜力學分析。姜景明[2]等以航空發動機附件平行軸傳動系統為研究對象，運用圖論理論建立系統傳動模型，以自定義比例疏遠度函數值為權值，進行系統構型生成、分析和優化。劉振濤等[3]以拓撲圖論為分析工具，采用分層圖論模型，根據完全圖理論對EVT（Electronic Variable Transmission，電控無級變速器）行星齒輪傳動系統建模，進行了基于能量流的全局最優化、EVT傳動方案性能仿真和分析。李劍鋒等[4]基于螺旋理論和圖論提出了正方形單元機構瞬時自由度計算公式，驗證了模型的正確性并解決了機構運動中自由度變化的問題。唐歲迎等[5]基于圖論法針對直升機傳動系統進行方案窮舉和篩選實現了傳動系統原理方案的自動生成。

旋翼無人機傳動系統較傳統航空器來說，向多發動機多旋翼方向發展，在傳動系統構型的生成過程中傳動級數不易過多，但可行的傳動系統方案集較大。借助圖論技術自動生成構型方案時，需要引入更多的約束條件、更加有效的評判標準。

1 傳動系統圖論

1.1 傳動系統圖論表示

圖論是研究集合元素之間二元關系的學科的一個分支，圖論研究這些拓撲的結構特性。圖論中的圖是客觀事物之間聯系的數學抽象，這種圖由頂點集和相應邊集構成。頂點代表事物，頂點之間的連線稱為邊，代表事物之間的聯系。圖的分析與研究過程中要對圖進行優化管理，基于流分析其基本問題包括最小費用最大流問題、最短路問題、最大容量路問題、最大流問題、最大利潤流問題、最小飽和流問題等。傳動構件的一種圖論表示方法如圖1所示。

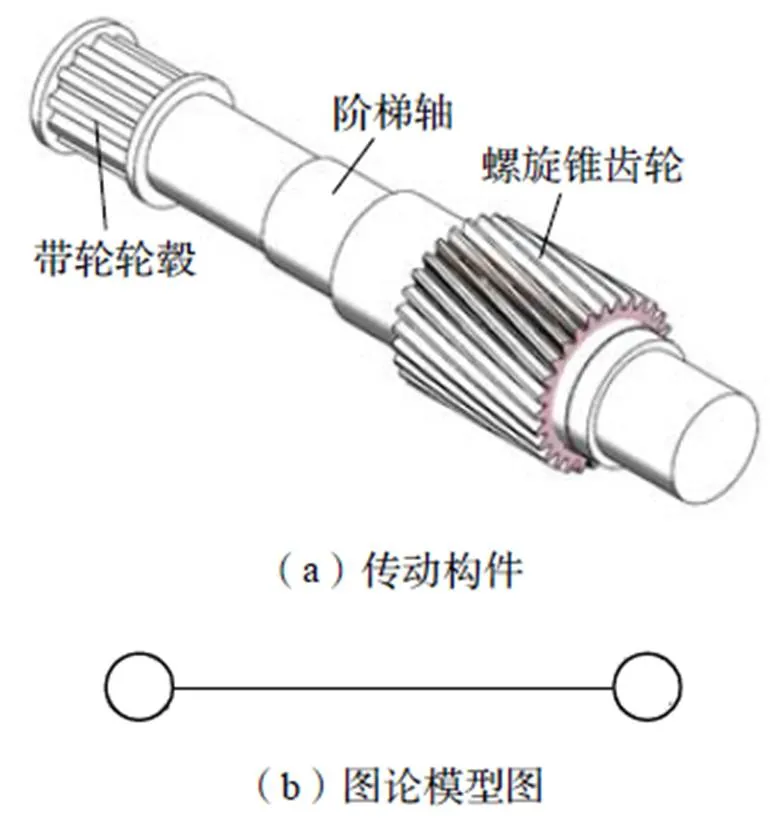
圖1 構件設計圖論模型圖

1.2 網絡流

將傳動系統用頂點與連線進行簡化，以矩陣()表示其頂點集，以矩陣()表示其邊集，以矩陣()表示其關聯矩陣，以矩陣()表示其鄰接矩陣，假設存在一個連通無環弧的有向圖，其滿足：

（1）頂點子集稱為發點集或源點集，其中每個頂點的入度都為0；

（2）頂點子集與不相交，其中每個頂點的出度都為0；

（3）每條弧都有一個非負的權值稱為弧的容量。

則可將其定義為一個網絡(,)，其由源點、匯點、中轉點組成，每條弧上都有傳輸能力的限制。

1.3 最小費用網絡流模型

對網絡(,)，其非線性最小費用網絡流問題可表達為：

滿足：

式中：為網絡中節點和弧的集合；為可微的費用函數；為網絡的發點；為網絡的收點；a為以、為端點的弧，其方向由指向；為網絡的可行流集合；e為弧a上的流；為網絡源點的凈輸出量。

2 無人機傳動系統功率流建模

無人機飛行器傳動系統是一個多輸入多輸出系統，某型飛行器傳動系統圖論模型如圖2所示。傳動系統中功率分流時，每條支路的流量占比與傳動比的分配無關，只與輸出負載有關。然而傳動比會影響功率流質量花費函數的計算，因此首先應基于熵權理論優化配比模型的傳動比分配方法[6]，對網絡中的邊進行傳動比分配，從而把傳動系統構型問題轉化為網絡上流的花費問題，如圖3所示。

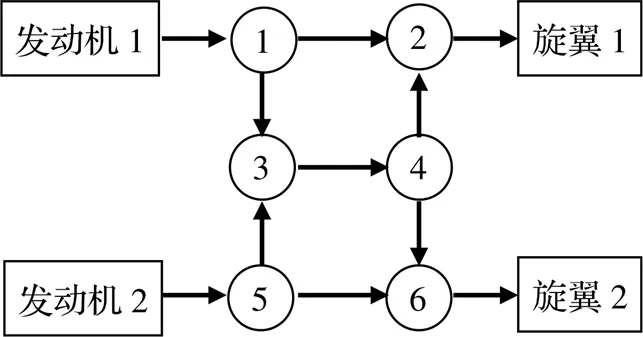
圖2 傳動系統網絡流模型示意圖

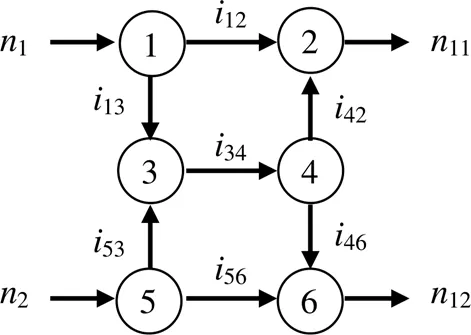
圖3 網絡流模型中的傳動比分配

將傳動系統構型問題轉化為非線性最小費用網絡流問題[7-8]時，給出如下定理，作為非線性網絡流的最優性定理：

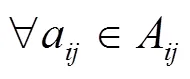
滿足：

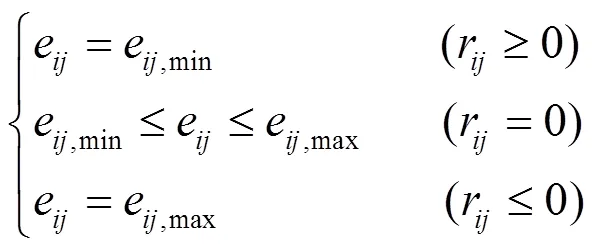
式中：A為給定網絡中弧的集合；r為流經弧a上的費用；e為弧a上的流。

在網絡中尋找一條費用最大的減廣路徑，即正向弧流量減少、負向弧流量增加，沿此路徑使發點的凈輸出量減小，數學描述為[9]：

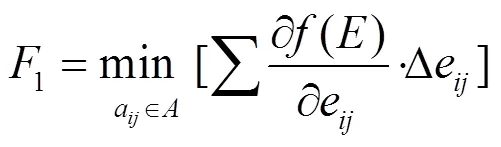
滿足：

式中：e為從節點到節點的弧a上的流量增量；為網絡發點；為網絡收點；為發點凈輸出量的變化值。

在網絡中尋找一條費用最小的增廣路徑，即正向弧流量增加、負向弧流量減少，沿此路徑使發點的凈輸出量增加，數學描述為：

滿足：

2.1 無人機傳動系統設計

傳動系統的設計與計算過程中，功率作為網絡中的流動變量，滿足網絡中流的屬性，對功率流的分析也是傳動系統構型設計中的必經步驟。功率是各傳動單元設計的依據，因此可以將功率流作為傳動系統構型設計時的主要設計參數。通過建立各個傳動構件及傳動軸的質量與功率流之間的函數關系，可以對整個傳動系統進行基于質量花費的功率流分析。質量與功率流之間的關系是非線性的，因此可以歸類為非線性最小費用網絡流問題。

對于非線性問題，求解時需反復迭代。各傳動單元的類型、所使用的材料等都會影響功率與質量間的關系，且同一構件、相同傳動比下質量也會是功率的非線性函數。因此需要大量經驗設計數據作為二者間關系求解的支撐。當二者間的非線性關系相當復雜時，也可根據實際情況設置一定的權值作為邊上的花費。

這里需建立一種網絡，它將以多種形式把指定動力裝置的能量傳遞到旋翼部件輸出；同時，從構件庫中選擇滿足一定約束條件的構件來實現功能傳遞的中間環節。具體步驟如下：

（1）從構件庫中選擇常用的構件，并對構件做基于屬性的分類。屬性包括傳動軸的空間角度改變量、旋轉構件旋向、功率容量限制等。

（2）假如傳動系統有個發動機、個旋翼，則系統共有條功率傳遞鏈路。尋找一組滿足約束條件的構件，完成從發動機到旋翼傳動功能的實現，此時，傳動系統的傳動級數為最小傳動級數。

（3）對同級的不同路徑上的相同構件進行合并，對可以實現相同傳動功能的構件進行并聯；同時進行構件傳動級數的擴展，即用多級傳動形式代替一級傳動形式，替代過程中必須保證傳動功能的一致。

某型無人機從發動機至旋翼之間傳動系統的所有部件，系統為單發動機雙旋翼輸出，發動機最大功率84.5 kW，額定轉速2386 r/min，旋翼最大轉速596 r/min，旋翼功率60 kW[10]。如圖4（a）所示。

按功能傳遞要求向(,1)、(,2)中添加實現傳動功能的構件。經上述分析，選取構件1和構件2，如圖4（b）所示。合并圖4（b）中的同級相同構件，得到圖4（c）。將圖4（c）中的兩條傳動鏈支路取相同頂點進行合并，得到兩級傳動系統模型，如圖4（d）所示。對兩級模型中的構件2，由于是齒輪變角度傳動，可以擴展為兩級傳動，如圖4（e）中可以用兩級錐齒輪傳動代替一級傳動。進一步得到單發雙旋翼傳動系統圖論模型，如圖4（f）所示。

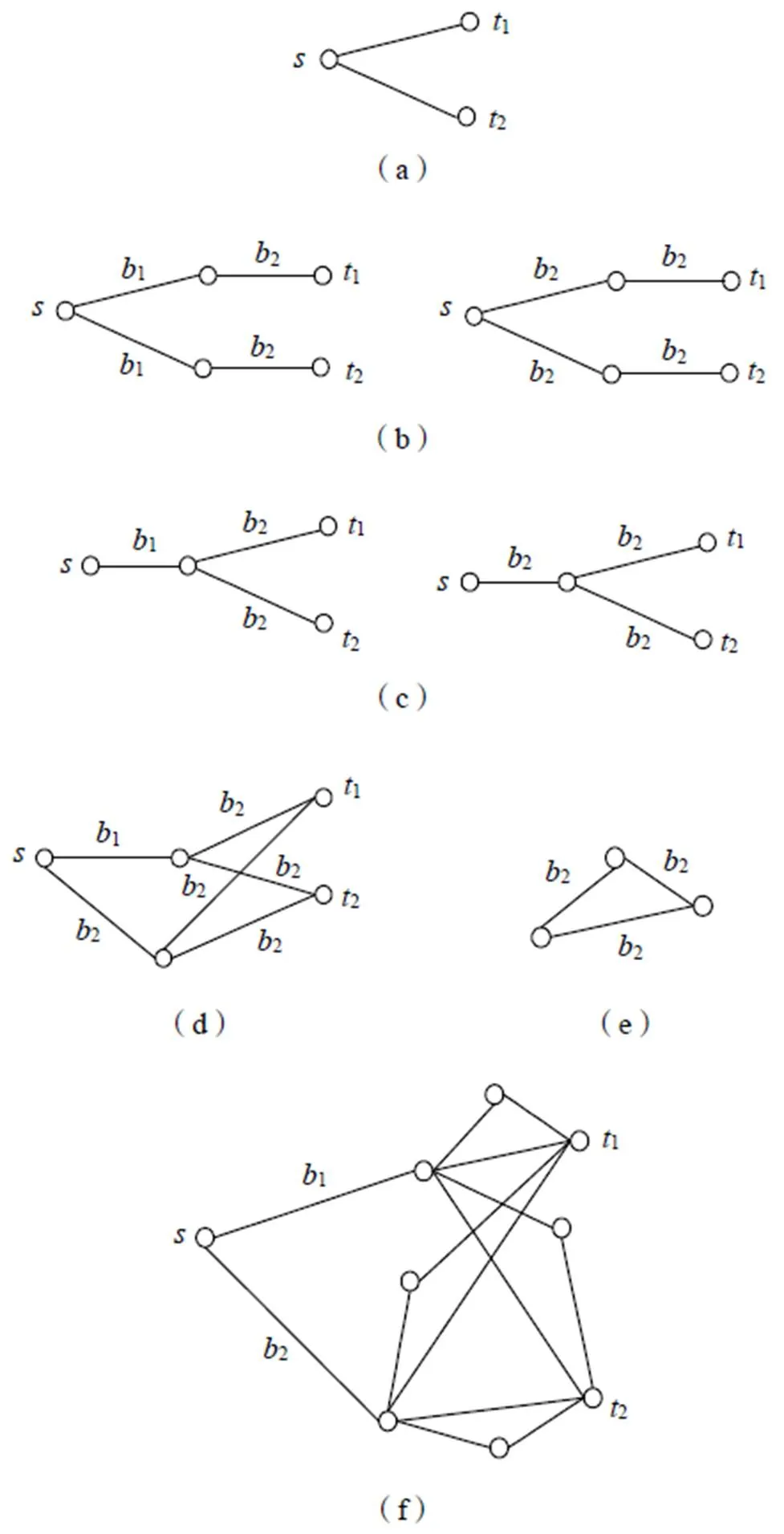
s為發動機輸入軸；t1、t2為旋翼輸出軸；b1為構件1；b2為構件2；b1、b2從帶傳動、錐齒輪、面齒輪和行星齒輪中選取。

2.2 功率流求解

基于最小花費功率流，采取線性加權的方法，對建立的傳動系統構型圖模型進行求解。

對兩級傳動系統模型（圖4d）進行分析，提取基于最小費用網絡流方法的初步信息和計算參數。

首先，作為下一步分析時的區分，對圖4（d）的中間層軸段進行標號，將經由構件1、2傳遞功率到的軸段分別標號為頂點1與頂點2，指代不同軸，如圖5所示。

圖5 兩級傳動系統模型標號圖

此時提取圖論模型特征，可以得到鄰接矩陣為：

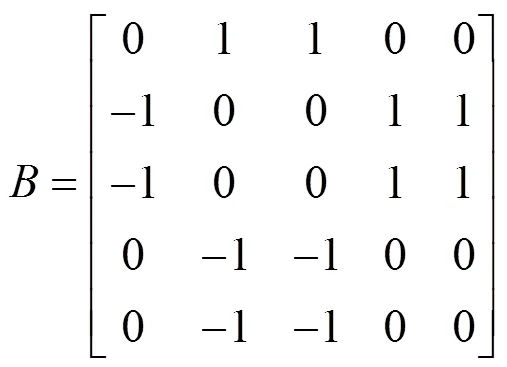
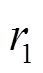
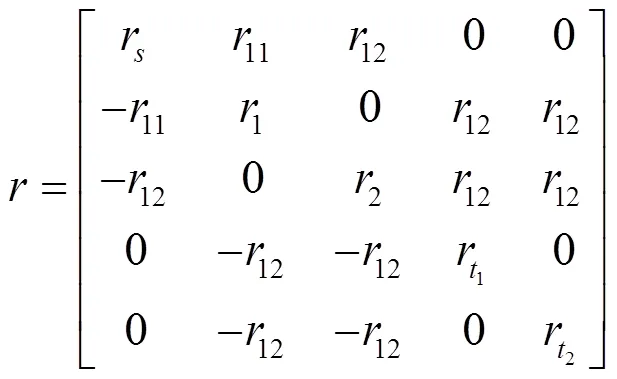
對兩級傳動系統模型，手動進行線性規劃分析。

設分析步長為1個功率單位，初始條件為：

則系統總花費為：

第1次迭代，即有1單位的功率流向(, 2)，此時：

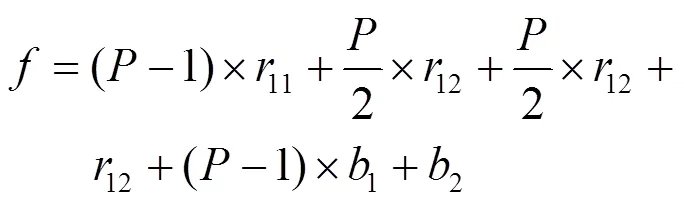
經多次迭代可以得到：

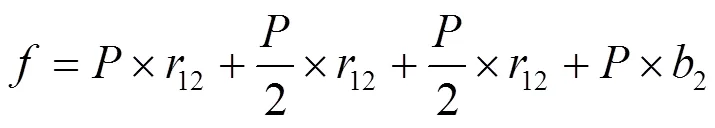
2.3 結果分析

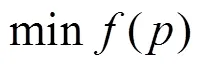
對該系統功率流鏈路進行分析，若各邊權重為功率值，則其關聯矩陣為：

發動機的輸入功率值為，旋翼輸出功率為1、2，則有：

對于一個固定傳動系統構型方案，經上述功率分析，可得傳動系統中任意邊上的功率值。對所有傳動系統構型方案進行功率分析，保留得到的功率值的最大值、最小值在min與max之間的方案，剔除剩余的傳動系統構型方案。

2.4 構型方案進一步優化

對生成的傳動系統構型方案集進行基于使用需求的初步篩選，需要考慮功能和結構兩個方面的約束問題。功能約束有空間角度、傳動比、回轉構件旋向、質量分布的對稱性、傳動效率和可靠性等。沿著功率流向，每個構件都會引起功率流向的變化；錐齒輪對總體空間位置改變的貢獻是一個角度范圍，一般為25°～155°。一些構件安裝位置的變動也會產生空間角度的變化，直齒輪對也會因為安裝位置不同產生空間角度的變化。當傳動系統確定時，可以建立三維坐標系，進行空間角度方面傳動系統的評估。每組構件都有一個輸入軸和一個輸出軸，輸入、輸出軸線的夾角，以同時垂直于旋翼軸和發動機軸線的向量為法向量，取得平面1，在平面1中取得旋翼軸與發動機軸線投影之間的夾角，作為系統輸入參數。

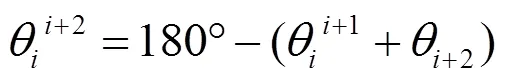
將每個構件視為一個對象，給它定義一個屬性值來作為方案篩選時判斷的依據。由于一些構件在設計參數未確定的情況下，其軸間夾角是一個范圍，可以將最小、最大夾角屬性值分別記為min、max。

在傳動系統的設計中，傳動比設計屬于總體設計，相應的傳動比為總體約束指標。一個完整的傳動系統有多級傳動構件，如何合理分配各級傳動構件的傳動比將直接影響到傳動系統的外形尺寸、重量、潤滑條件、成本、構件的圓周速度及精度等級。傳動比分配原則指出：

（1）分配后各級傳動比的承載能力要求近似相等；

（2）在此傳動比條件下，傳動系統的潤滑條件最為便捷；

（3）傳動系統總體積與重量最小。

一般的傳動比分配方法是選擇傳動構件傳動比的參考范圍的中值，或是利用經驗公式對各級傳動比進行估計與遞推，進而通過調整其中某一構件的傳動比來滿足總的傳動比要求。這種方法操作簡單，但存在人為主觀分配的局限性，因此在傳動系統構型設計的過程中通常采用基于Willis重量最小的衍生傳動比分配方法和基于熵權理論優化配比模型的分配方法。其中，基于Willis重量最小的衍生傳動比分配方法是在保證系統總體積最小的條件下，理論上計算出系統應該具有的傳動比的分配方法。

由于基于Willis重量最小的衍生傳動比分配方法在設計過程中可能會取到構件常用傳動范圍之外的值，且該方法只給出了一對傳動軸之間構件傳動比的計算推導公式，當它擴大到整個傳動系統時計算將變得復雜，準確度降低，因此出現了基于熵權理論的傳動比分配方法。該方法是建立一個傳動比評價指標分級矩陣，根據評價指標的差異來修正各傳動比的權值，對傳動比參考區間的中值進行加權。評價指標分級矩陣是將各傳動構件的參考范圍進行分級，分為等差數列作為評價指標分級矩陣的一行。

假設有個構件將其傳動比參考范圍分為級等差數列，則指標數據矩陣為：

對指標矩陣標準化，得到標準規一矩陣為：

第個構件的第項指標所占的比重為：

從而第項指標的熵值為：

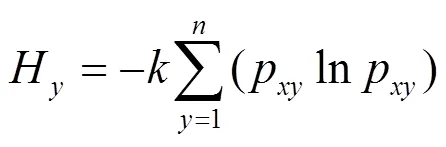
系統的熵權為：

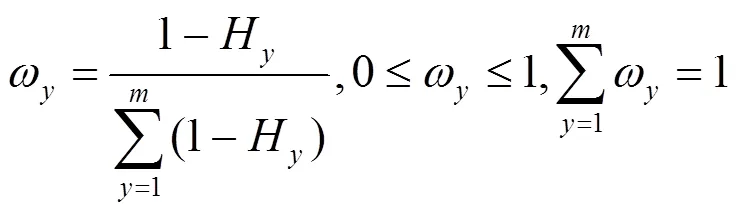
此時，系統傳動比分配優化模型為：

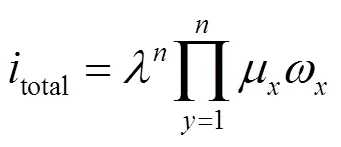
式中：為構件傳動比參考范圍的中值；為引入常量，由總的傳動比計算得出。

傳動系統構型設計包括設計出系統基本結構尺寸，以滿足強度要求。這些強度、性能要求就是系統設計時需要滿足的結構尺寸約束。齒輪在設計過程中應采用合理的尺寸，以滿足齒根彎曲疲勞強度及齒面接觸疲勞強度，并保證齒輪擁有一定的抗點蝕、抗膠合能力。同時，齒輪的支撐跨距和齒寬受到結構布局的約束；齒輪總體結構受傳動系統總質量的約束，所采用尺寸盡可能使構件擁有最小質量。本文對質量這一約束做了詳細研究，結果表明，該約束能很好地評價得到的方案集的優越性。

3 結論

本文利用最小費用網絡流模型對無人機傳動系統圖論模型進行了分析。得到以下結論：

（1）基于功能導向的傳動系統圖論模型建立方法可以得到更為全面的傳動系統構型初始方案集；

（2）設計過程提取了傳統系統功率這一特征，把傳動系統看成功率流網絡，從流的角度對系統進行分析，進一步進行構型方案的自動生成是可行的；

（3）將傳動單元各自的質量作為功率流的指示參數之一進行網絡流的分析時，可以作為基礎約束條件對生成的構型方案進行初選。

同時，該方法可減少設計過程中的人為干預，有利于突破思維局限，提高設計效率。為傳動系統計算機自動生成方案提供理論參考。

[1]E. Pennestrì，F. Freudenstein. A Systematic Approach to Power- Flow and Static-Force Analysis in Epicyclic Spur-Gear Trains[J]. International Journal of Advanced Robotic Systems，1993（115）：639-644.

[2]姜景明，王三民，李浩. 航空附件平行軸傳動系統方案設計的智能化方法[J]. 機械科學與技術，2018，37（2）：324-328.

[3]劉振濤. EVT混合動力傳動系統的圖論建模與構型綜合設計理論研究[D]. 重慶：重慶大學，2016：16-20.

[4]李劍鋒，王三民，智常建. 基于螺旋理論的正方形單元及其組合機構瞬時自由度分析[J]. 西北工業大學學報，2017，35（5）：863-869.

[5]唐歲迎，吳立言，楊小輝. 直升機主減速器傳動系統運動方案生成技術研究[J]. 機械傳動，2017，41（4）：28-33.

[6]李沛剛. 基于功構模式的產品概念設計理論和方法研究[D]. 濟南：山東大學，2010：12-16.

[7]李明哲. 圖論及其算法[M]. 北京：機械工業出版社，2010：169-185.

[8]謝平榮，賈仁安. 網絡流優化高效智能算法及其應用[M]. 北京：科學出版社，2015：16-30.

[9]Sahani N A. Envelope protection systems for piloted and unmanned rotorcraft[D]. The Pennsylvania State University，2005：52-70.

[10]唐林. 自動化概念設計中機構功能的識別[J]. 機械傳動，2000，17（12）：39-42.

Configuration Design of Unmanned Rotorcraft Based on Graph Theory

WANG Xiangsheng，LIN Wenqi，HAN Xuanxuan，YUAN Yuwen，SONG Wenjin

( Northwest Institute of Mechanical and Electrical Engineering, Xianyang 712099, China )

The transmission system as the core system of unmanned aerial vehicles, to a certain extent, determines the performance of the aircraft. In order to solve the problem of low efficiency of traditional transmission system design, this paper proposes a transmission system configuration design method based on graph theory. Firstly, the graph theory, including graph-theoretic representation of transmission system, the theory of network flow, and minimum cost network flow, are introduced. Secondly, we propose a method for power flow modeling of unmanned rotorcraft transmission system. A digital model is established through computer automated transmission ratio distribution. Power flow is analyzed and the optimal transmission system configuration scheme is obtained. Finally, taking a single dual-engine rotor drive system as an example, the drive system configuration analysis is carried out by using the proposed method of minimum cost network flow analysis to verify the rationality of the method proposed and the correctness of using constraints. It establishes the foundation for the computer automation design of the subsequent unmanned rotorcraft transmission system.

transmission system configuration；graph theory；unmanned rotorcraft；power flow

TH132

A

10.3969/j.issn.1006-0316.2022.02.003

1006-0316 (2022) 02-0015-07

2021-04-22

王向勝（1992－），男，甘肅會寧人，碩士，主要研究方向為機械動力學、傳動構型設計、結構設計分析，E-mail：1421779947@qq.com。