汶川地震災區小流域洪水模擬及不確定性分析

孫聿卿，郭曉軍，陳興長，張 菊

（1.西南科技大學環境與資源學院，四川綿陽 621000；2.中國科學院山地災害與地表過程重點實驗室/中國科學院水利部成都山地災害與環境研究所，四川成都 610041；3.中國科學院青藏高原地球科學卓越創新中心，北京 100101）

引言

山洪不但直接威脅山區人民群眾的生命財產安全，也是泥石流等山地災害最直接的激發因素。“5·12”汶川地震后，山洪泥石流在震區小流域集中、大規模、頻繁暴發，給人民生命財產造成巨大損失。如2010年“8.13”強降雨造成災區各地暴發群發性山洪泥石流災害，其中紅椿溝泥石流沖出約7×105m3物質堵斷岷江，文家溝沖出3×105m3物質淤埋清平鄉場鎮，均形成堰塞湖等鏈式災害［1］；2013年“7·10”強降雨激發都汶公路沿線多個流域暴發泥石流，其中七盤溝沖出規模達7×105m［1］，洱溝沖出物質超過5×105m3［2］，造成岷江河道多處堵塞；2019年“8·20”強降雨再次導致該路段暴發泥石流，交通干線中斷通行達2個月；2020年夏季的持續強暴雨再次造成大范圍的山洪泥石流災害。災害預報是最直接有效的防災減災措施，具有重要的防減災意義。而采用科學合理的方法進行洪水峰值流量計算，是山洪和泥石流預報的重要環節。

小流域的洪峰計算方面，目前有適宜于特定地區的經驗公式、小流域計算公式和水文模型等方法。在汶川地震災區，有學者通過設計不同頻率的暴雨，利用水文模型對流域徑流過程進行模擬［3］；通過水文觀測和數值模擬，發現小流域徑流峰值隨降雨量的增加存在非線性激增現象［4］；基于流域清水流量，采用雨洪修正法計算不同雨型條件下的泥石流流量變化特征［5］。但上述研究都存在一個共性問題，即沒有用實際監測資料進行充分驗證，而模型驗證是水文計算中極為重要的部分，是保障計算準確性和科學性的基礎。

汶川地震災區小流域坡高谷深、地形復雜，降雨的空間不均勻性極大；自然環境艱苦、災害頻發，實際水文數據監測和獲取極為困難。降雨和徑流時間監測數據的缺失造成無法評估各種計算方法的合理性和所選擇參數的準確性，因此，模型的應用存在很大的不確定性，體現在模型結構、模型輸入及模型參數等各個方面［6-8］等。針對這個現狀，本文作者對災區一個典型小流域（洱溝一支溝）開展了數年的降雨和徑流監測，并以該流域為研究對象，基于水文計算方法模擬徑流過程，利用實際降雨和洪水監測資料，驗證模擬過程，在此基礎上探討劃分子流域和不同時間步長對模擬結果的影響，尋求該地區小流域洪水的最佳模擬方案。

1 研究區概況

選取四川省汶川縣洱溝下游右岸支溝-禾家溝為研究對象。該小流域流域面積約2.4 km2，主溝道長約2.6 km，流域最高海拔為3 100 m，最低海拔為1 200 m，平均坡度達43.4°，溝道平均縱比降為280‰，流域整體自西南向東北方向延展（圖1）。坡面的松散物質主要由古元古代康定巖群的斜長角閃巖、混合片麻巖、變粒巖等變質巖組成。該小流域可進一步劃分為3個部分，W-I為流域下游，面積約0.7 km2，溝道長約1.3 km，溝道平均縱比降約為260‰；W-Ⅱ和W-III分別為上游2個支溝，W-II流域面積約1.3 km2，溝道長約1.2 km，溝道平均縱比降約330‰；W-Ⅲ流域面積約0.4 km2，溝道長約0.7 km，平均縱比降約380‰。

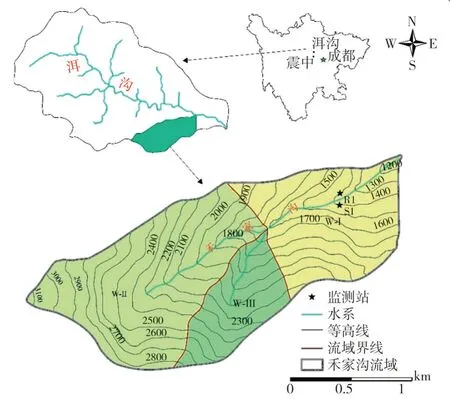
圖1 研究區地形圖Fig.1 Topographic map of the study area

流域溝口年平均降雨量約1 200 mm［2］。“5·12”地震對該流域造成嚴重的影響，大量的坡體垮塌物堆積于溝谷中，為山洪泥石流的暴發提供了豐富的松散物源。2013年7月10日和2019年8月20日，洱溝兩次暴發大規模泥石流，沖出物質均超過5×105m3，掩埋溝口工廠等基礎設施，且對岷江河道造成巨大影響；2014～2016年的實際監測表明，該流域多次暴發中小規模泥石流，且形成模式均以洪水徑流沖刷溝床物質為主［2，9］，因而洪水流量的準確計算對于該流域及都汶地區類似流域的泥石流起動和流量估算都具有重要意義。

2 研究方法和數據來源

2.1 模擬方法

（1）模型構架

本文產流計算采用SCS曲線法，坡面匯流、河道匯流計算采用Kinematic wave（運動波）方程。SCS曲線是根據降雨累積量、土地利用現狀、植被發育、土壤水分狀況等因素發展而來的經驗曲線［10］，其數學表達如下：

式中，Q為t時刻的產流量（mm），P為t時刻的累積降雨量（mm），Ia為初始損失量（mm），S為最大流域降雨最大潛在損失量（mm）。美國土壤保持局通過分析大量的降雨徑流數據發現Ia與S的經驗關系式為［10］：

而實際應用中將S定量表達為不同下墊面產流能力的綜合指標-徑流曲線數（CN）：

因此，用SCS曲線法分析產流過程的關鍵參數是CN值，即產流系數，與土壤類型、土地利用、土壤前期濕潤程度等有關，通過C N值表可查算。一般地，產流系數越高，產流量越大［11，12］。

運動波方程原理是將流域概化為明渠，輸入值為凈雨量，基于此來計算明渠的非穩定水流方程，模擬其徑流過程。表達式如下：

式中，h為水深（m），t為時間（s），q為單寬流量（m2/s），x為坡面某點距坡頂的水平距離（m）；ie（t）為t時刻坡面上距離坡頂x米處的單寬凈雨量（mm），S0為坡面坡度，n為曼寧粗糙系數。

坡面匯流的主要參數為坡面長度、流域坡度、粗糙系數等，溝道匯流的主要參數為溝道長度、溝道坡度、溝道斷面形狀、曼寧系數等。基本的斷面、尺寸信息通過影像或現場測量獲得，曼寧系數可查表估算。

（2）流域模型和降雨輸入

基于研究區5 m分辨率的地形數據，通過填洼、計算流向、匯流、生成河網、劃分子流域、確定出水口等，提取河道長度、坡度、最長水流路徑、流域坡度、流域面積、流域中心點位置等基本流域特征參數，最終獲得流域地形模型。單次降雨模擬中，最重要的輸入是場次降雨過程。根據流域內部實測監測資料，整理出需要的場次降雨過程，將實時降雨數據整理為5 min、10 min、30 min和60 min雨量序列作為模型的輸入。

2.2 數據來源

研究所需數據來源于2014-2016年洱溝流域內部的降雨和徑流監測數據。選擇位于禾家溝流域內部的雨量站R1和位于禾家溝溝口的流量監測站S1（監測參數：流速和水位，見圖1）。其中降雨監測利用0.5 mm的翻斗雨量計實時記錄降雨過程，流體表面流速和水深分別采用雷達測速儀和超聲波水位計監測，流量計算采用公式Q=a·V·A，其中a取0.6［13］，V表示流速，A表示溝道過水斷面面積。

3 模型的總體計算效果

本文選取2014-2016年間的6場典型降雨數據進行模擬和驗證試驗，各次降雨的基本情況如表1所示。

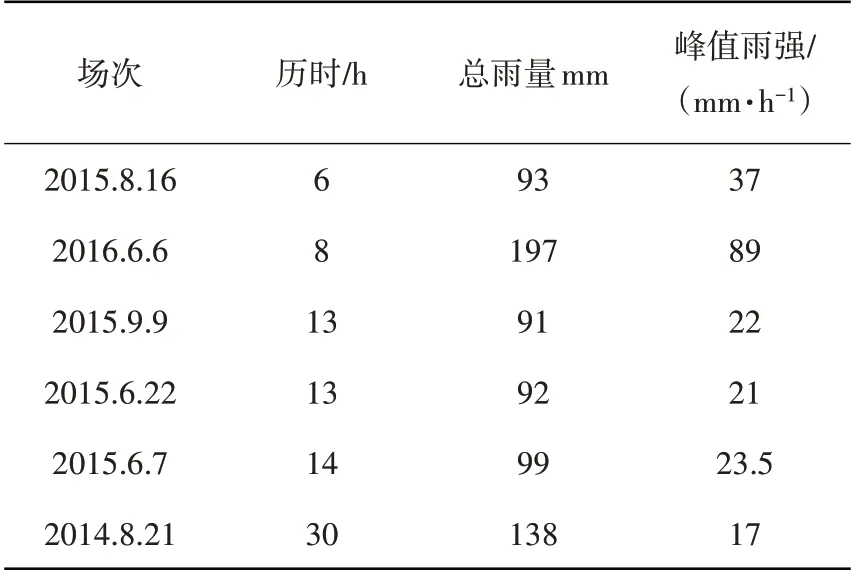
表1 2014－2016年間各場次降雨情況Table 1 Rainfall in each session from 2014 to 2016

根據各場次降雨的雨型和總雨量，選取2015.8.16、2015.9.9、2015.6.7三場降雨作為模擬對象，用以大概確定模型參數范圍，三場降雨的歷時分別為6、13、14h，峰值雨強分別為37、22、23.5 mm/h，總雨量在91～99 mm之間。同時針對性選擇2016.6.6、2015.6.22和2014.8.21三場降雨驗證計算結果，各場次降雨歷時分別為8、13、30 h，可代表短歷時和長歷時降雨，峰值雨強分別為89、21、17 mm/h，總雨量在92～197 mm之間。

模型需要的流域特征參數如坡面長度、坡度、河床寬度、河床長度等可通過實地考察和地形分析得到，計算過程參數如C N、坡面粗糙系數n1、溝道曼寧系數n2等可根據流域實際情況通過查表獲得初始值作為參考，進而進行人工調整，以達到模擬效果的最優化。研究區地表土壤類型以砂黏土、砂土為主，上游植被覆蓋主要是林地，中下游受到地震的影響，裸露滑坡體較多，部分滑坡體上逐漸有矮草和灌木叢恢復。參考美國水土保持局手冊［10］以及目前國內外SCS模型應用的研究成果［14-17］，確定C N的初始輸入值為70。根據研究區地表狀態查表（USACE，1998）［10］選擇粗糙系數0.3，曼寧系數0.08［9］作為初始值。退水過程的主要參數流量衰減系數初始值取0.9。劃分子流域時，各子流域的初始基流量按流域面積大小分配。

首先將小流域視為一個整體進行集總式模擬計算，模擬時間尺度為5 min，徑流過程見圖2至圖4（模擬過程線1），計算結果見表2。

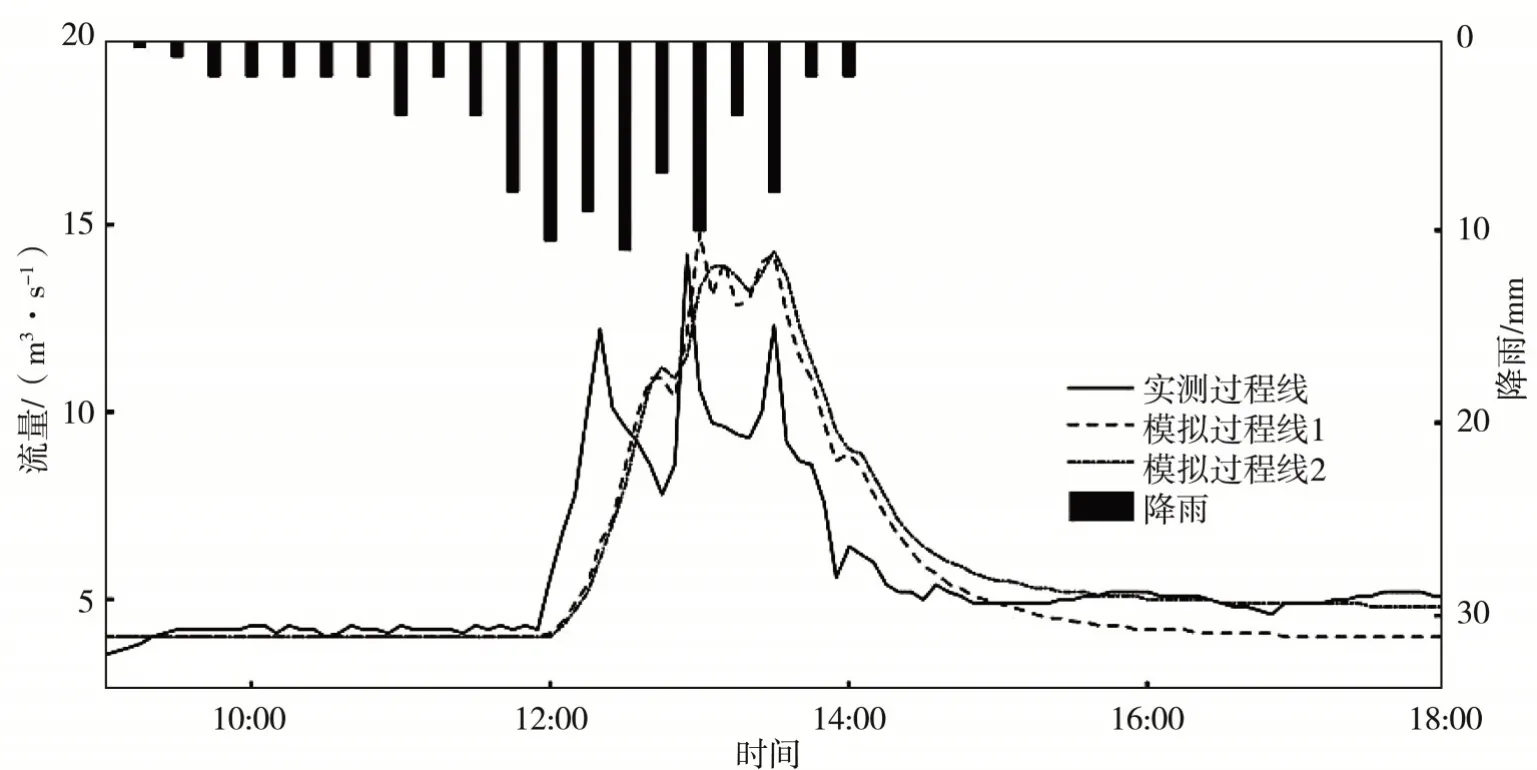
圖2 2015.8.16場次模擬過程Fig.2 The rainfall?runoff process simulation on Aug.16，2015

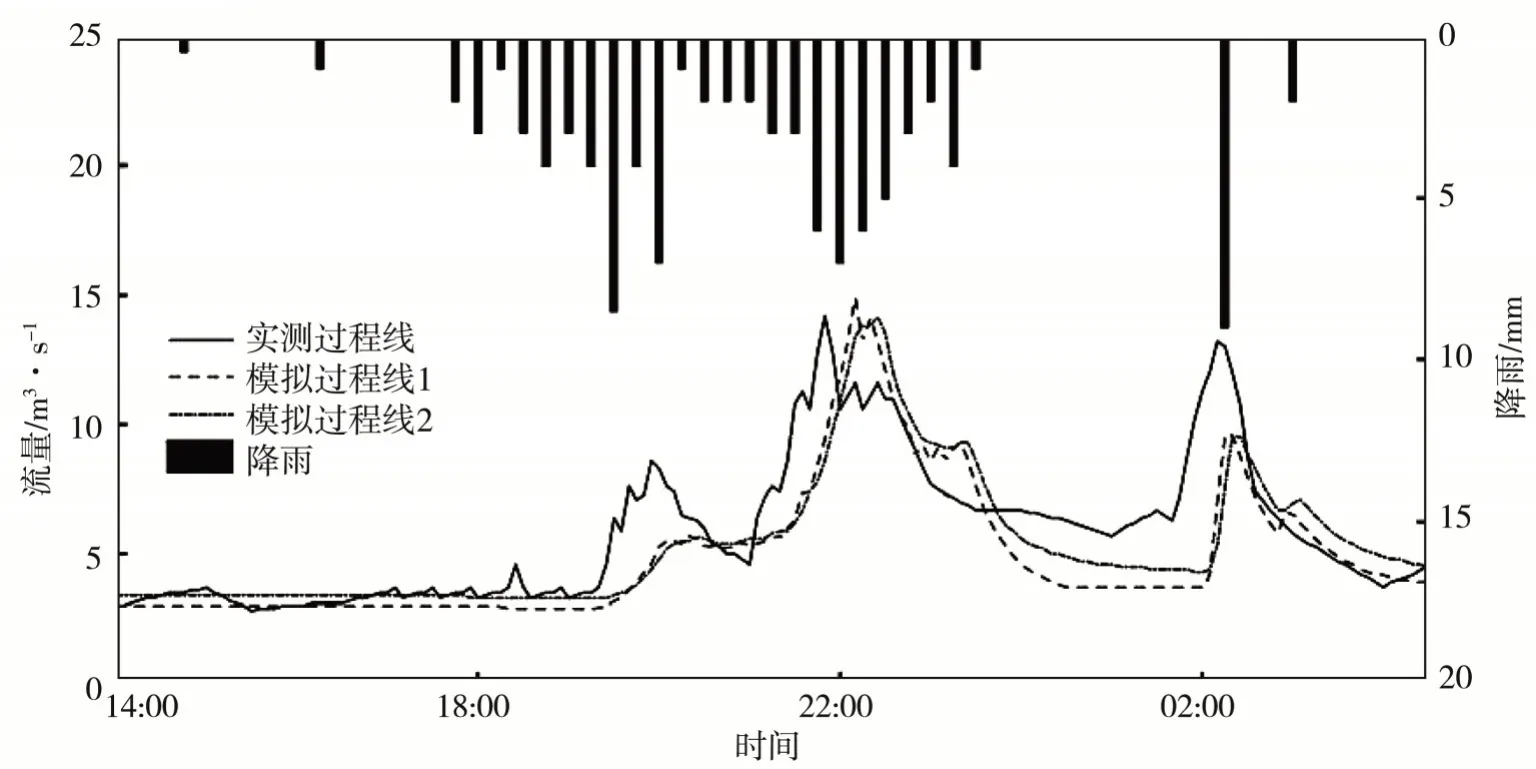
圖4 2015.6.7場次模擬過程Fig.4 The rainfall?runoff process simulation on Jun.7，2015

本文針對的對象為降雨-洪水，在模擬效果的評價中，不以傳統的Nash?Sutcliffe系數和相關系數R2等作為指標，而以洪水致災最關心的3個要素：峰現時間、洪峰流量和洪水總量作為評價指標，三場降雨的模擬結果為：

（1）2015.8.16場次（圖2）：模擬的徑流過程線與實測的徑流過程線基本一致；模擬的峰現時間比實測滯后5 min，洪峰流量14.8 m3/s，誤差為4.23%，洪水總量20.8×104m3，誤差為-4.09%。

（2）2015.9.9場次（圖3）：該次洪水有兩個峰值，模擬的徑流過程線與實測的徑流過程線基本一致，可模擬出兩個峰值；第一次模擬的峰現時間比實測滯后5 min，洪峰流量14.6 m3/s，誤差為1.39%，洪水總量30.0×104m3，誤差為14.27%；第二次模擬的峰現時間與實測一致，洪峰流量11.2 m3/s，誤差為1.82%。

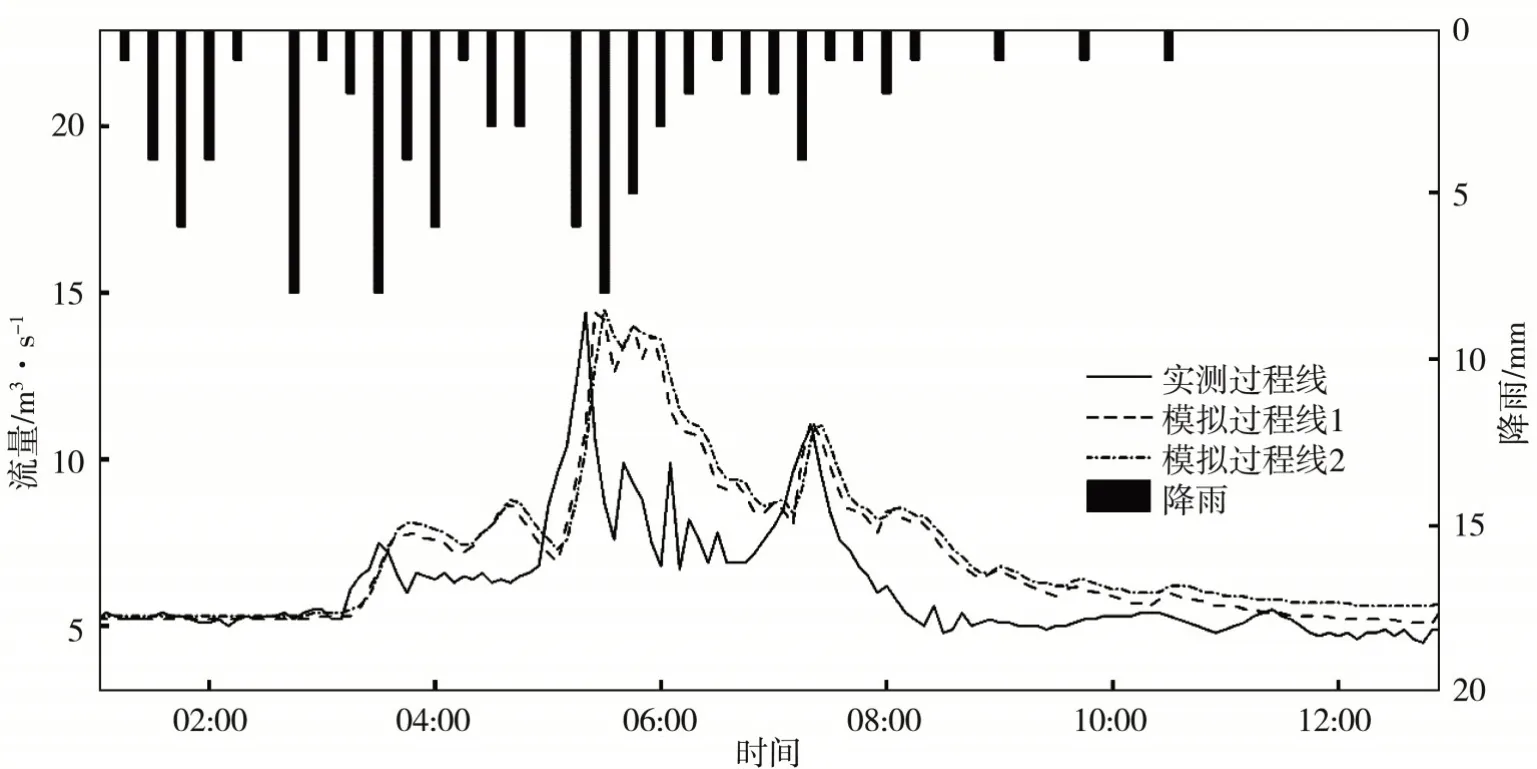
圖3 2015.9.9場次模擬過程Fig.3 The rainfall?runoff process simulation on Sep.9，2015

（3）2015.6.7場次（圖4）：該次洪水有多個峰值，模擬的徑流過程線與實測的徑流過程線基本一致；第一次模擬的峰現時間比實測滯后20 min，洪峰流量14.9 m3/s，誤差為4.93%，洪水總量25.3×104m3，誤差為-15.88%；第二次模擬的峰現時間比實測滯后5 min，洪峰流量誤差為-27.27%，洪峰值偏小。

由模擬效果可見，考慮到山區洪水數據獲取和模擬的困難程度，3個關鍵指標的誤差均在誤差允許范圍內。另外，本文在模型中選擇的關鍵參數時，n1、n2基本保持一致，均為0.3、0.08，CN值在69～72之間，相對比較確定。因而，在驗證階段的3場降雨中，以CN=70，n1=0.3，n2=0.08作為初始參數，峰值流量誤差均在3%以內，結果見圖5至圖7，證明了模型參數選擇的合理性。若優化CN至最佳模擬效果，其取值也在69～72之間。

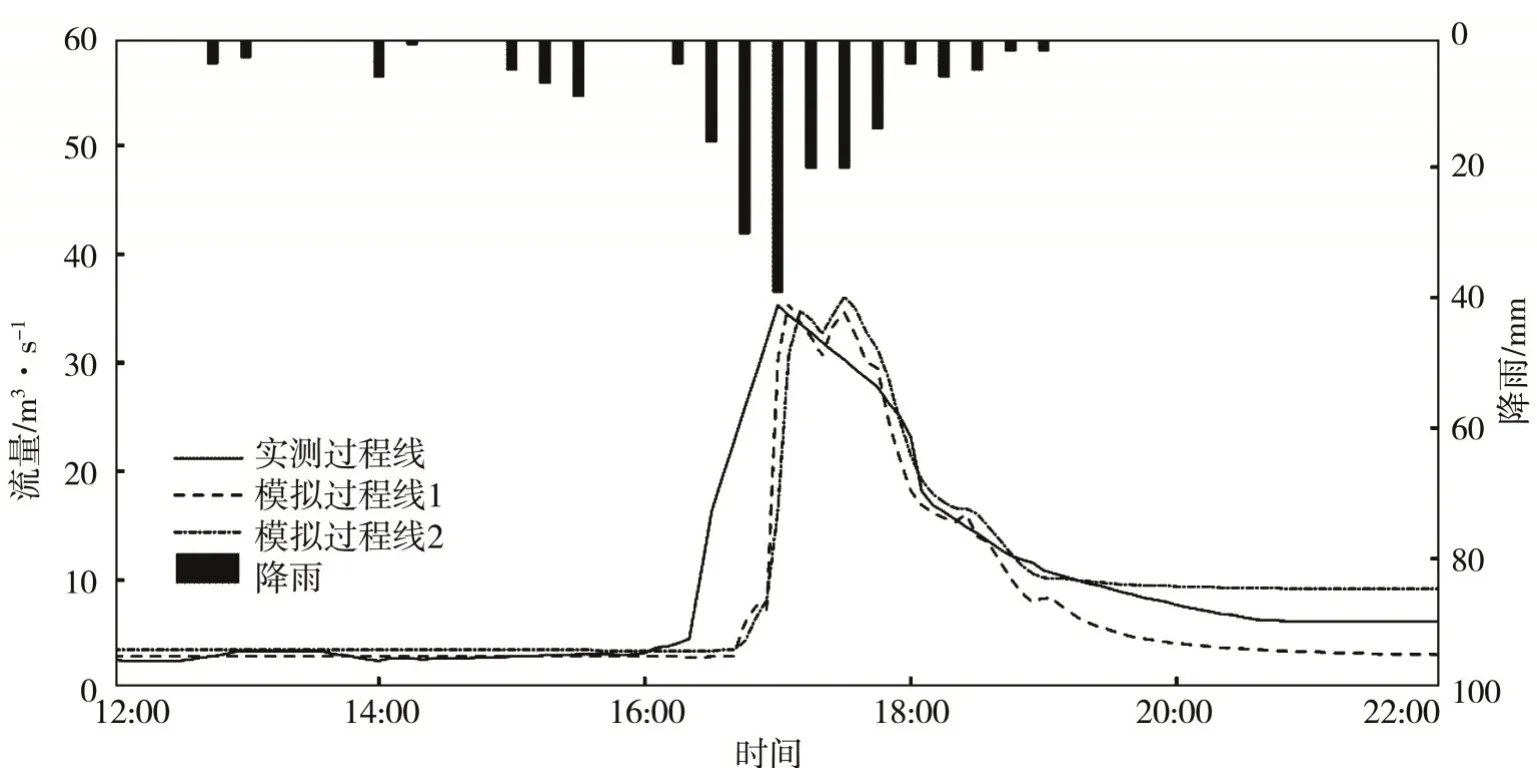
圖5 2016.6.6場次模擬過程Fig.5 The rainfall?runoff process simulation on Jun.6，2016

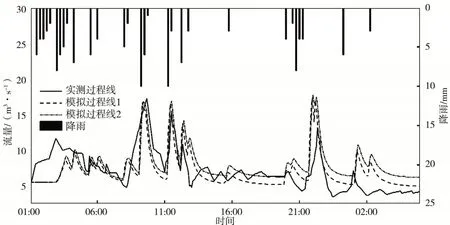
圖7 2014.8.21場次模擬過程Fig.7 The rainfall?runoff process simulation on Aug.21，2014

（1）2016.6.6場次（圖5）：模擬過程線與實測過程線基本一致；模擬峰現時間比實測滯后5 min，洪峰流量35.5 m3/s，誤差為0.57%，洪水總量25.9×104m3，誤差為-22.79%；

（2）2015.6.22場次（圖6）：模擬的徑流過程線形態上雖與實測有一定差異，但模擬結果基本能反映峰現時間與峰值流量。峰現時間比實測滯后5 min，洪峰流量僅相差0.1 m3/s，洪水總量相比較偏小，誤差為-14.31%；

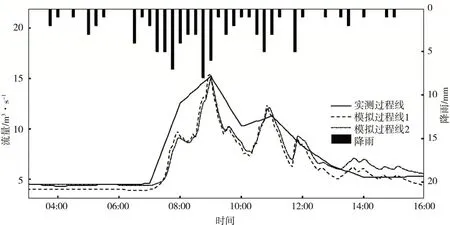
圖6 2015.6.22場次模擬過程Fig.6 The rainfall?runoff process simulation on Jun.22，2015

（3）2014.8.21場次（圖7）：模擬的徑流過程線與實測的徑流過程線基本一致，模擬結果能呈現多個洪峰，由于該場次歷時較長，降雨過程復雜，模擬的后期洪峰流量與實測值仍存在一定偏差，洪峰值偏大；模擬的峰現時間比實測提前20 min，洪峰流量17.0 m3/s，誤差為-2.86%，洪水總量77.2×104m3，誤差為-0.9%。

綜上，率定期和驗證期的6個場次模擬結果顯示，峰現時差范圍為-20～20 min（峰現時間為正表示峰現時間滯后，為負表示峰現時間提前），洪峰流量誤差范圍為-2.86～4.93%，洪水總量誤差范圍為-22.79～-10.52%。考慮到山區洪水數據獲取和模擬的困難程度，此3個關鍵指標的誤差均在可接受范圍內。同時，模型關鍵參數n1、n2基本一致，均為0.3、0.08，C N值在69～72之間，相對比較確定。由此可見，本文所選參數有效，模型可推廣用于類似無資料地區的洪水估算。

4 子流域劃分和時間步長對模擬結果的影響

4.1 劃分子流域對計算結果的影響

為進一步探尋模型在小流域洪水模擬中的使用方案，將禾家溝流域劃分為3個子單元進行分布式模擬，并與上述集總式模擬的結果相對比，以分析劃分子流域與否對模擬結果的影響。三個子流域的CN值根據面積權重分配作為初始輸入值：

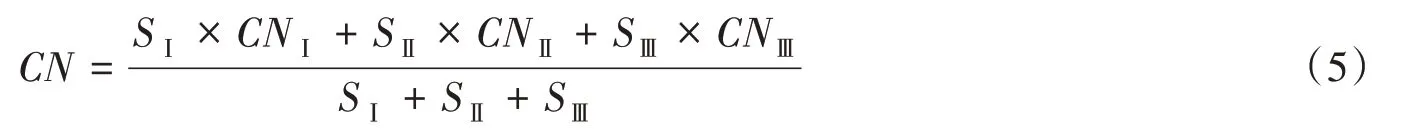
各場次模擬過程對比見圖2至圖7（模擬過程線2），模擬結果對比見表2。

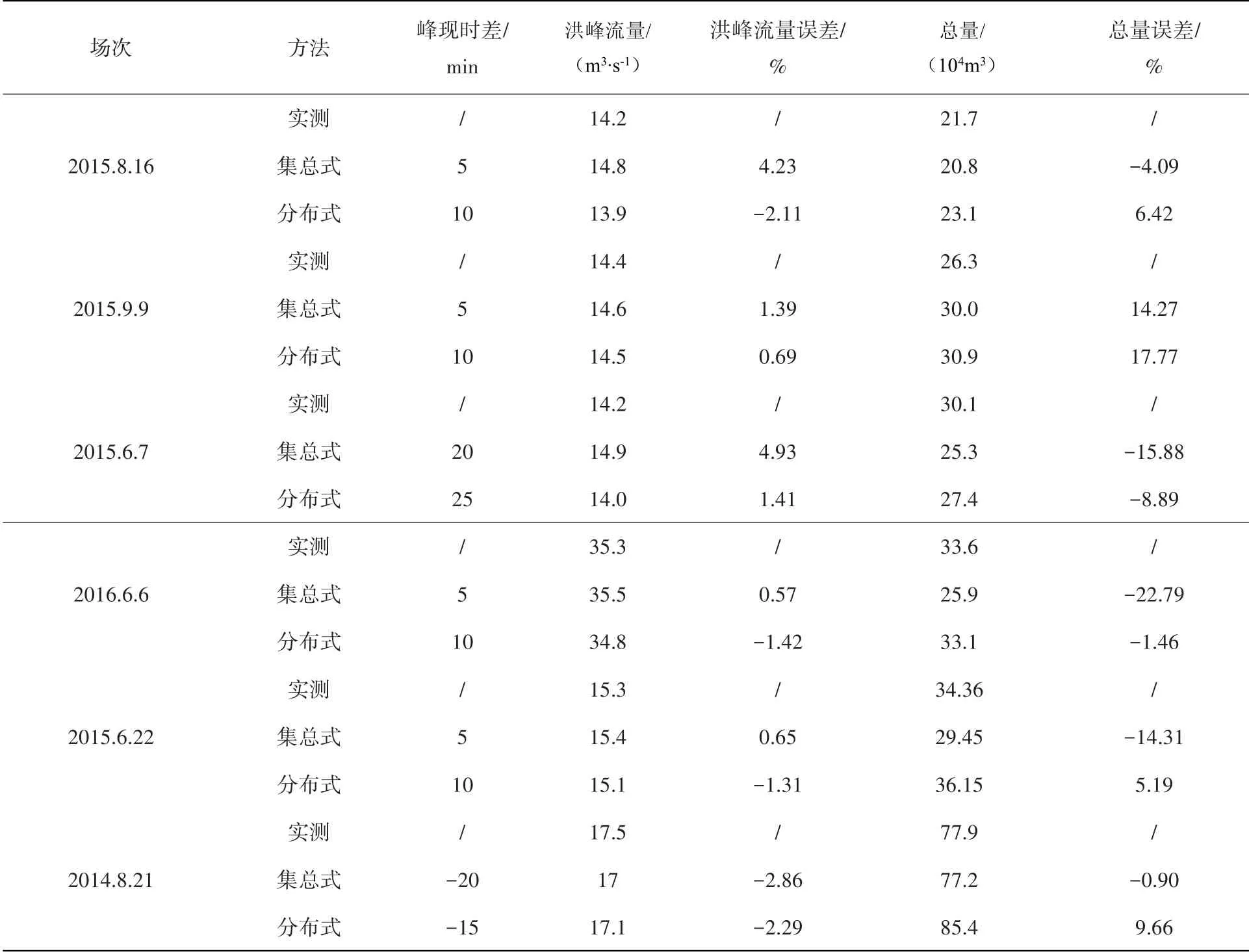
表2 各場次模擬結果匯總Table 2 Summary of simulation results of each rainfall event

結果顯示，2種模擬方式的過程線基本一致；分布式模擬中洪峰流量誤差范圍為-2.29～1.41%，平均值為-0.83%，總量誤差范圍為-8.89～17.77%，平均值為4.78%。在峰值流量與洪水總量的模擬上比集總式模擬的精度有小幅度提升；峰現時差范圍為-15～25 min，比集總式模擬往往有5 min左右的延遲，這是由于集總式模擬忽略了子流域內部匯流過程，而流域單元的細化考慮了子流域內部溝道的匯流過程，延長了河道匯演時間，導致峰現時間滯后。

考慮到分布式模擬在一定程度上增加了參數設置的工作量，在實際應用時往往造成參數難以確定，可能出現異參同效的現象，且對模擬結果的提升有限，在針對類似地形高差大、坡陡且參數難以獲取的極小流域水文計算時，集總式模擬是簡單易行的方案。

4.2 不同降雨時間步長對計算結果的影響

為探討降雨輸入的時間步長對模擬結果的影響，在參數不變的情況下，輸入時間步長分別設置為5 min、15 min、30 min、60 min，分析6場降雨的洪水模擬過程，結果見圖8～圖13所示，各場次結果見表3。

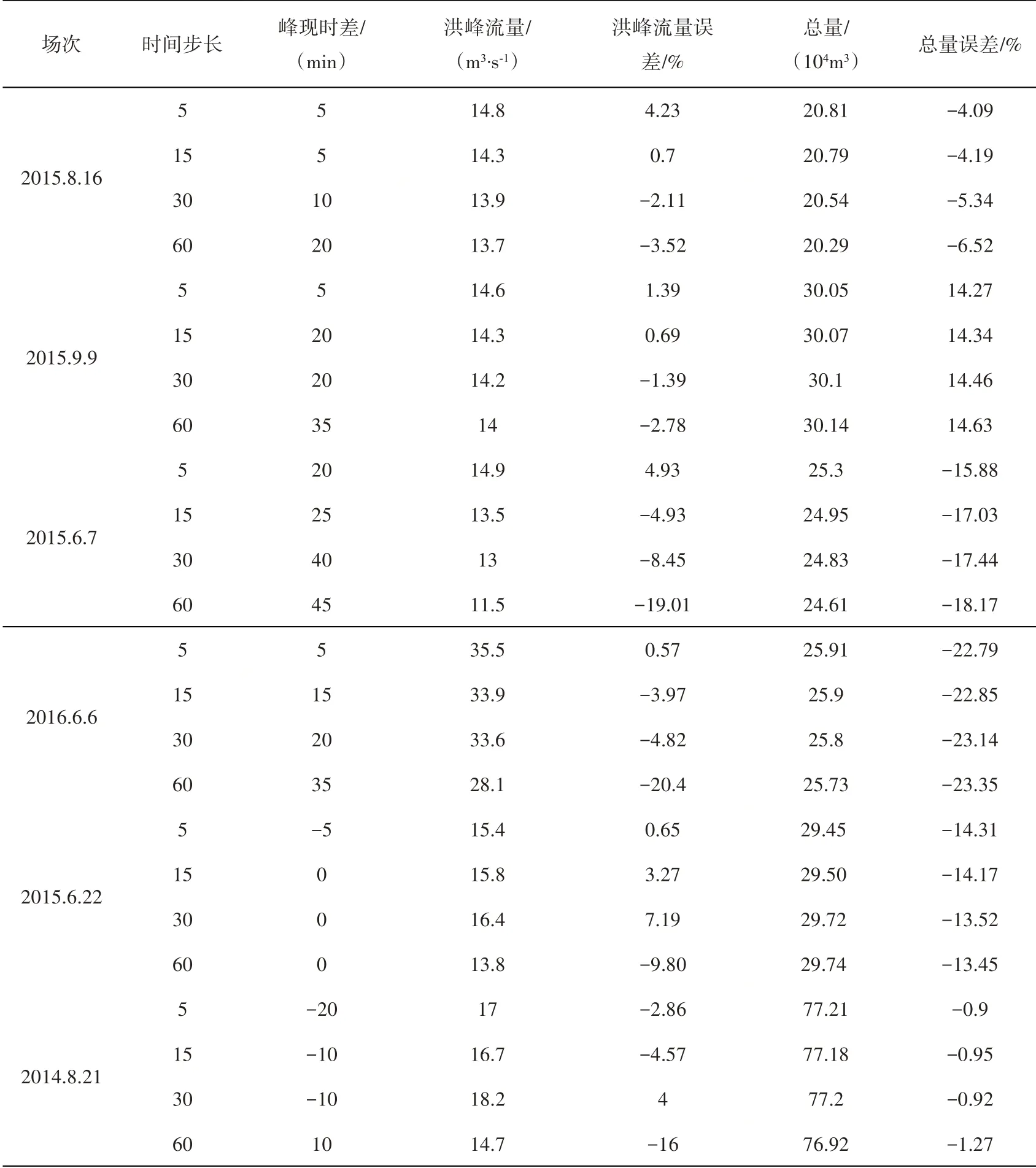
表3 不同時間步長下各場次的模擬結果匯總Table 3 Summary of simulation results of each rainfall event under different time steps

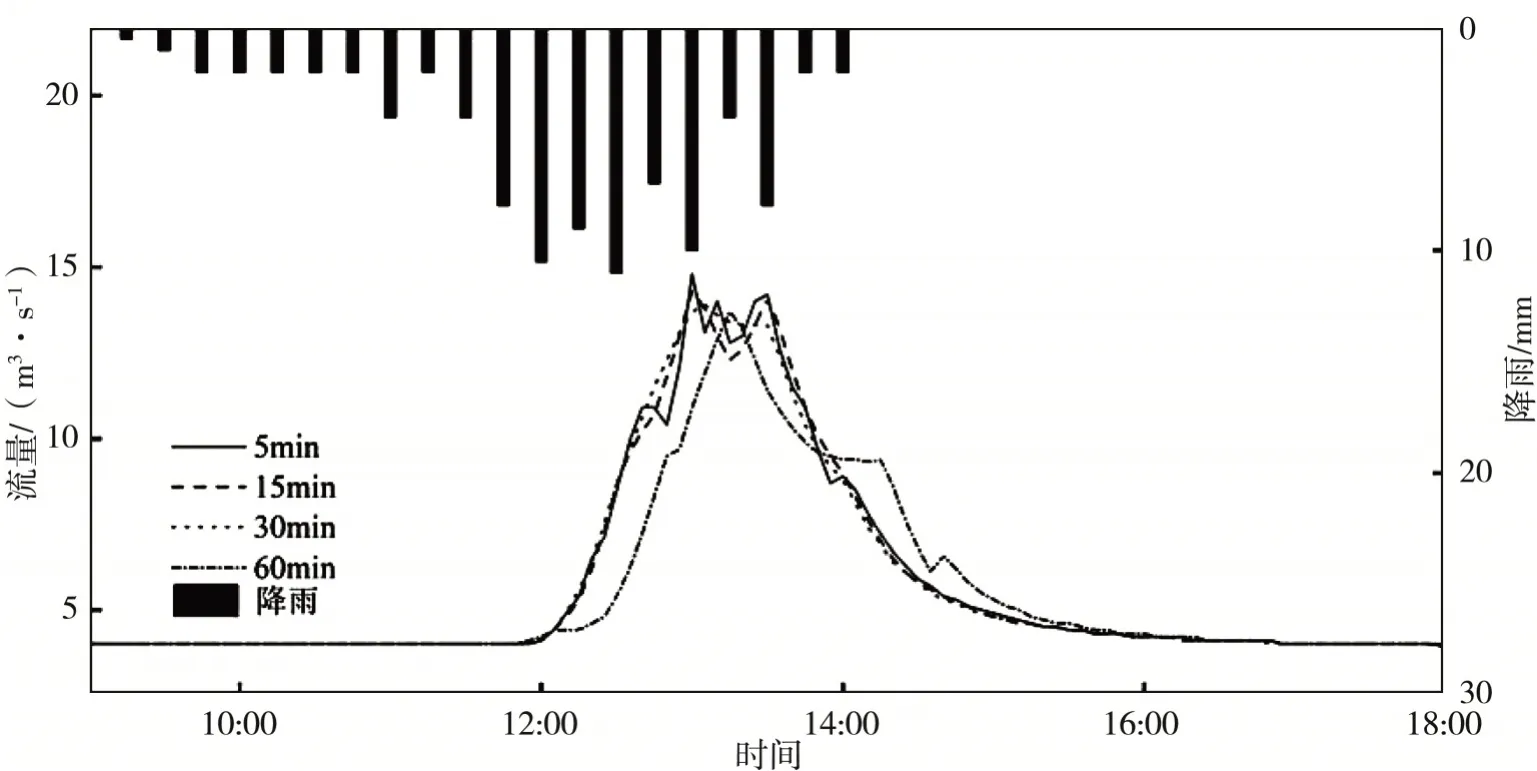
圖8 不同時間步長下2015.8.16場次的徑流過程對比Fig.8 Comparison of rainfall-runoff processes under different time steps on Aug.16，2015

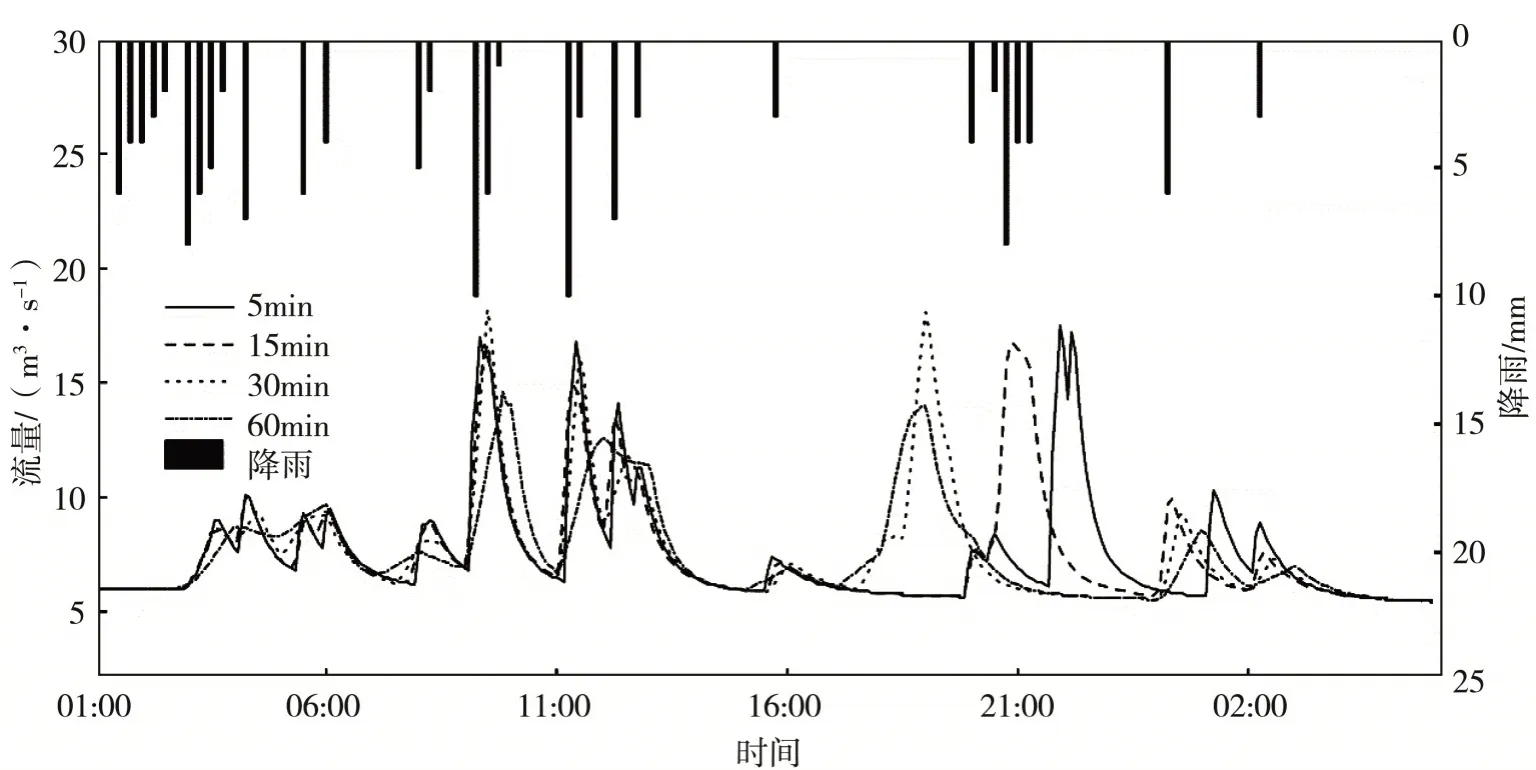
圖13 不同時間步長下2014.8.21場次的徑流過程對比Fig.13 Comparison of rainfall?runoff process of different time steps on Aug.21，2014

（1）2015.8.16場次（圖8）：該場次不同時間步長的徑流過程線基本一致；峰現時差范圍在5～20 min之間，其中步長5 min和15 min的峰現時間一致，均滯后5 min，洪峰流量和洪水總量差距不大，總體逐步減小。

（2）2015.9.9場次（圖9）：該場次不同時間步長的徑流過程線在前期基本一致，第二次峰值差異較大，步長增加，洪峰值降低，過程線逐漸坦化；步長為5 min時洪峰現時滯后5 min，步長為15 min和30 min時洪峰現時均滯后20 min，60 min時滯后35 min，洪峰流量和洪水總量差異不大，總體趨勢減小。

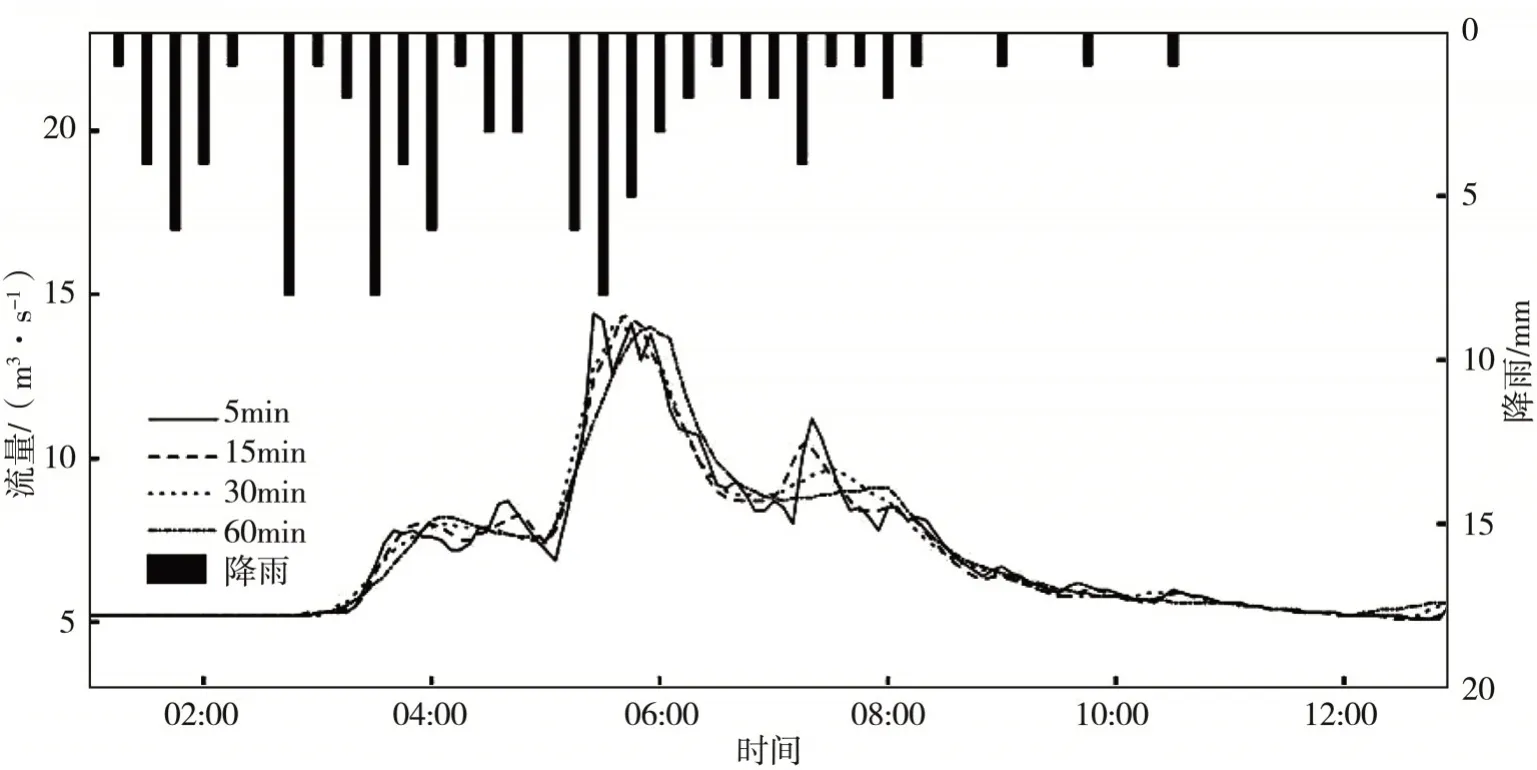
圖9 不同時間步長下2015.9.9場次的徑流過程對比Fig.9 Comparison of rainfall-runoff processes under different time steps on Sep.9，2015

（3）2015.6.7場次（圖10）：該場次不同時間步長的徑流過程線差異明顯，步長為60 min的徑流過程線更加坦化，峰值流量明顯降低；步長越大，時差越大，滯后時間從20 min遞增至45 min，洪峰流量和洪水總量逐漸減小。

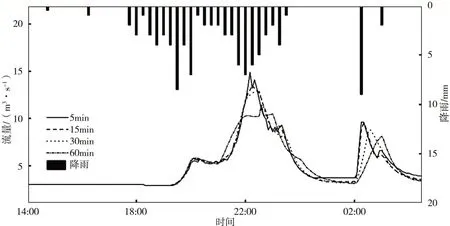
圖10 不同時間步長下2015.6.7場次的徑流過程對比Fig.10 Comparison of rainfall-runoff process of different time steps on Jun.7，2015

（4）2016.6.6場次（圖11）：該場次不同時間步長的徑流過程線基本一致，相較步長為60 min的徑流過程線更加坦化，趨于平緩；峰現時差從5 min遞增至35 min，洪峰流量從35.5 m3/s遞減至28.1 m3/s，誤差從0.57%逐步變為-20.40%；洪水總量誤差均保持在20%左右。

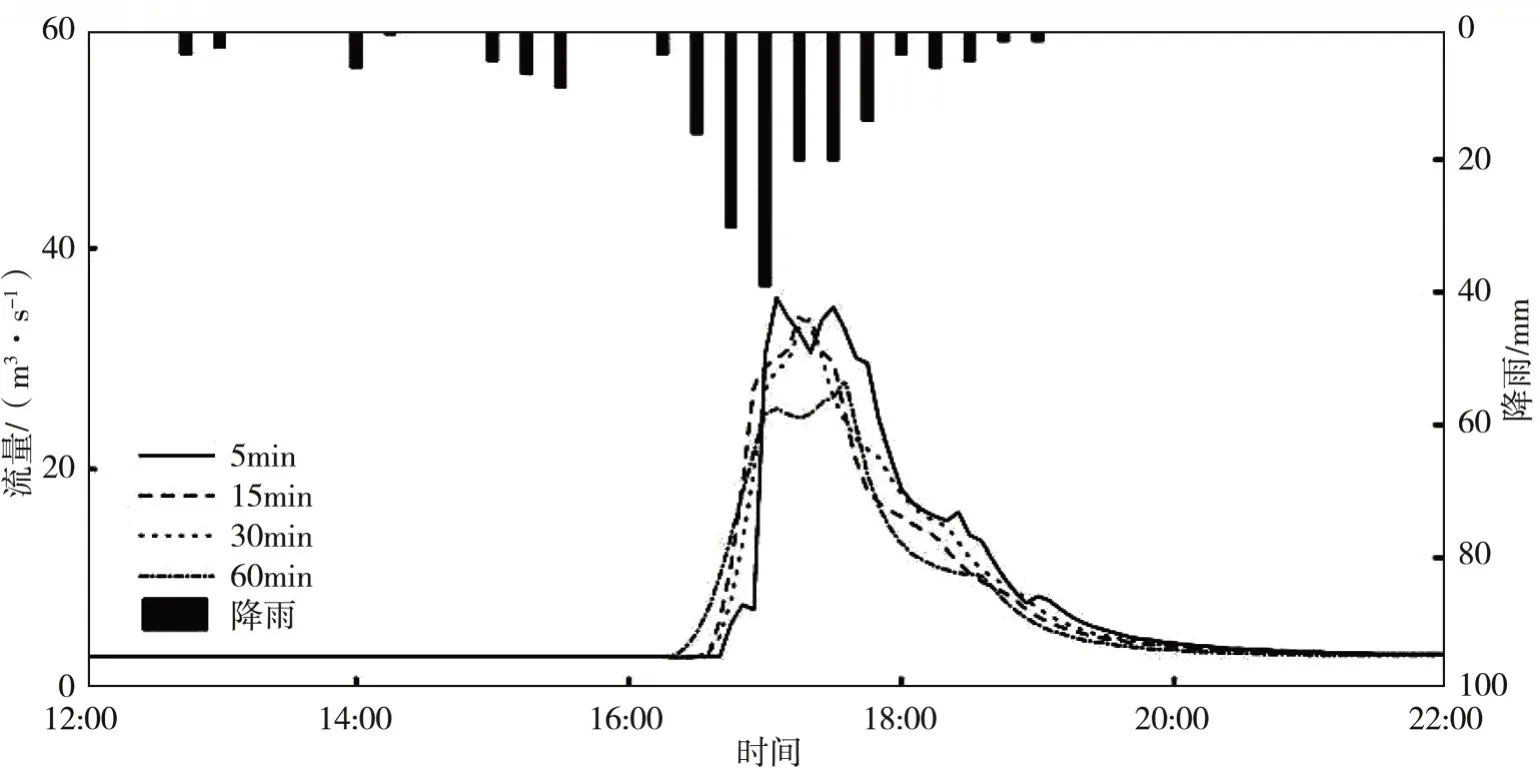
圖11 不同時間步長下2016.6.6場次的徑流過程對比Fig.11 Comparison of rainfall-runoff processes under different time steps on Jun.6，2016

（5）2015.6.22場次（圖12）：該場次不同時間步長徑流過程線的形態基本一致，步長為60 min的徑流過程線有一定坦化；步長為15、30、60min的峰現時間一致，但相比5 min是滯后的，洪峰流量以及洪水總量，前3個步長差異不明顯，但當步長增加到60 min時，峰值明顯降低。

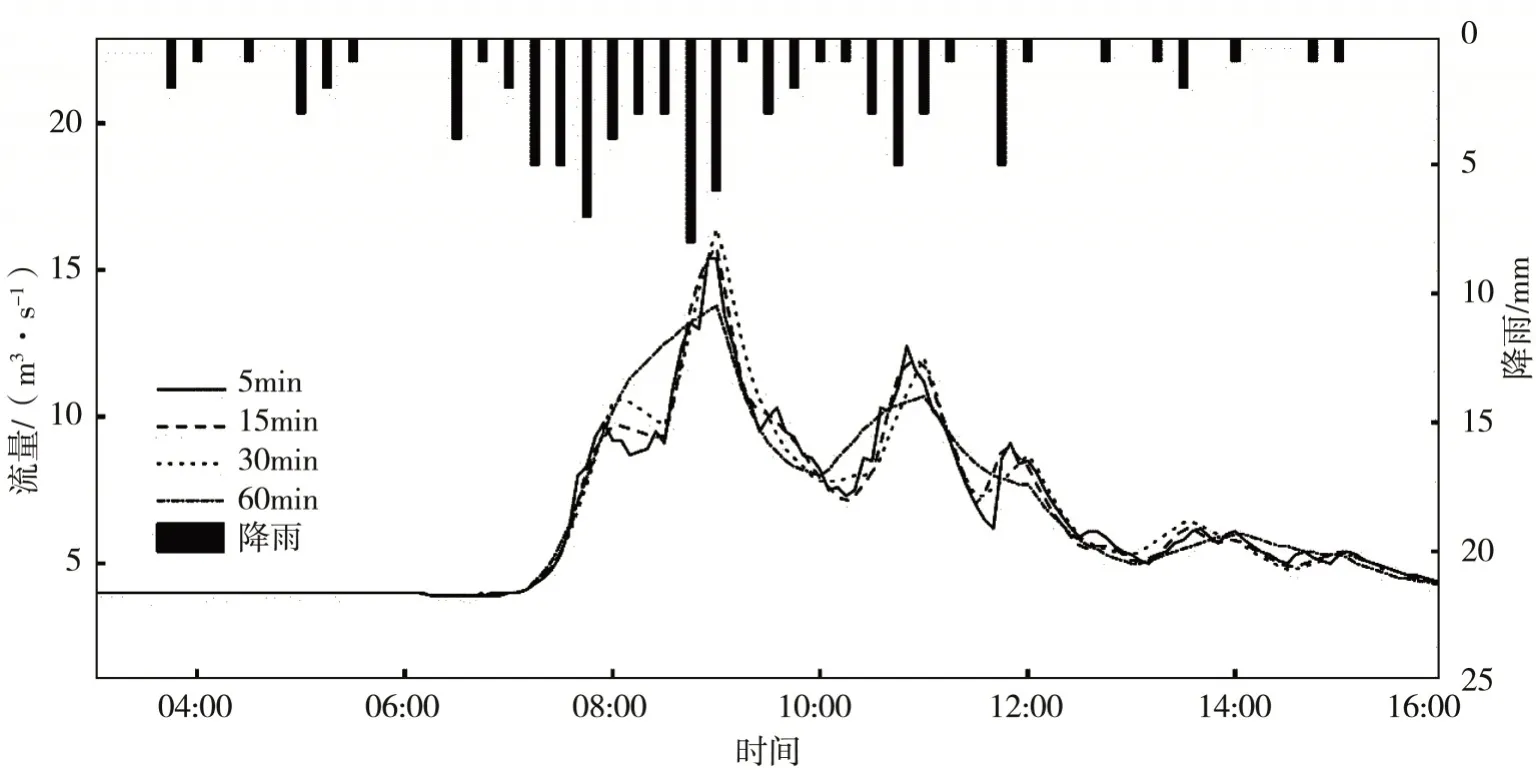
圖12 不同時間步長下2015.6.22場次的徑流過程對比Fig.12 Comparison of rainfall-runoff processes under different time steps on Jun.22，2015

（6）2014.8.21場次（圖13）：該場次降雨較為復雜，不同時間步長的徑流過程差異較大，第一次洪峰現時隨步長增加而滯后，第二次洪峰峰現時間隨步長增加而提前；時間步長為5～30 min時，峰現時差均比實測值提前，60 min步長的模擬峰現時間滯后10分鐘；洪峰流量從17.0 m3/s遞減至14.7 m3/s，洪水總量差異不大，誤差保持在1%左右。

由此可知，時間步長的變化會對模擬過程線產生一定影響，尤其是60 min步長的模擬結果，雖也基本可模擬出峰值，但在洪峰流量和峰現時間等方面與5 min步長有較大差異。

（1）隨著模擬時間步長的增加，峰現時間逐漸滯后，步長為5 min的峰現時差范圍為-20～5 min，步長為15 min的峰現時差范圍為-10～25 min，步長為30 min的峰現時差范圍為-10～40 min，而步長為60 min的峰現時差范圍為10～45 min。時間步長越精細，峰現時間的誤差越小，反之會一定程度上推遲峰現時間。

（2）隨著模擬時間步長的增加，洪峰流量總體趨勢呈降低趨勢，徑流過程線趨于坦化，這是由于時間間隔的增加引起單位降雨強度的降低，削弱了洪峰流量。洪水總量的變化不大，這是由于雖然相對雨強降低，但總降雨量并未發生變化，因此，總產流量基本不變。

綜上所述，初始雨量數據精度越高，時間步長越短，模擬效果越理想，即要求我們在進行洪峰模擬預報時，原始的雨量數據應盡可能的精確。但是在實際應用中，受限于環境條件，實際觀測數據精度不夠高，故應選擇合適的時間步長進行徑流計算。

5 結論與討論

本文采用SCS產流模型和運動波方程，對震區一個小流域（2.4 km2）進行洪水模擬。從結果來看，對洪峰三要素包括洪水總量、峰值流量和峰現時間都能較好模擬。與實際監測資料相比，模擬的洪峰流量誤差最大不超過5%，峰現時間誤差在-20～20 min之間，洪水總量模擬誤差在-22.79～14.27%，說明該方法可用于地震災區小流域的水文計算。

在模型主要參數（CN和n）的確定過程中，首先根據經驗值或查表值作為初始值，然后根據模擬結果進行調整，雖有一定的經驗性，但歷次降雨的CN最優值都在69～72范圍內，因此相對合理且方便應用。模型對于長歷時、多峰的復雜降雨中，在保障第一次峰值模擬精度的情況下，對后續洪水的峰值流量模擬效果較差。這是由于復雜降雨過程中峰值前的前期降雨造成流域產匯流條件發生改變，而模型并不能準確模擬該過程。

對于2 km2尺度的小流域，劃分子流域的分布式模擬效果比將流域作為一個整體集總式模擬效果略好，但提升較為有限，考慮到西部山區流域參數獲取的難度，分布式模擬可能造成參數輸入的人為主觀性，因此集總式模擬是可行的。降雨時段的控制和模擬時間步長對洪水過程模擬影響較大：在保持參數一致的情況下，隨著時間步長的增加，模擬的峰現時間通常會滯后，且洪峰流量逐步偏小，徑流過程線不斷坦化。

實際監測資料是洪水等災害發生機理研究和模擬計算的重要支撐，而目前由于自然環境惡劣、無傳輸信號、災害頻發、施工條件危險艱苦等諸多困難，在汶川地震災區尚無一個小流域擁有豐富的監測資料。本文利用位于流域內部的降雨和徑流數據，研究對象為震區一個具有數年監測歷史的2 km2左右尺度的小流域，具有較高的代表性。但在推廣應用時仍需考慮山區降雨的高度不均勻性和野外水文監測的復雜性，監測結果和研究結果仍具有一定的不確定性。