船閘水域船舶列隊(duì)協(xié)同停船預(yù)測(cè)控制器

雷超凡 初秀民 柳晨光 吳文祥 李松龍

1.武漢理工大學(xué)國(guó)家水運(yùn)安全工程技術(shù)研究中心，武漢，4300632.武漢理工大學(xué)智能交通系統(tǒng)研究中心，武漢，4300633.武漢理工大學(xué)交通與物流工程學(xué)院，武漢，430063

0 引言

作為溝通水系、提高航道等級(jí)、改善水流條件的通航建筑物，船閘一直是內(nèi)河航運(yùn)基礎(chǔ)性控制節(jié)點(diǎn)[1]。船閘水域航運(yùn)智能化水平的不足會(huì)嚴(yán)重制約內(nèi)河智能航運(yùn)的發(fā)展。提高過(guò)閘安全性和效率是船閘智能化的重要目標(biāo)。由于船閘水域船舶航行具有區(qū)域受限、間距緊密、操縱困難等特點(diǎn)，因船舶操控失誤而引發(fā)的閘室浮式系船柱損壞、閘門(mén)被撞等事故時(shí)有發(fā)生。此外，目前廣泛采用人工操控船舶依次進(jìn)出閘室的過(guò)閘方式，缺少對(duì)船閘內(nèi)各船舶的集中調(diào)控，這種過(guò)閘方式是制約船舶過(guò)閘效率提升的重要原因[1-2]。在閘室內(nèi)多船協(xié)同精確停船控制能夠顯著縮短船舶在船閘水域的滯留時(shí)間，增加閘室空間的利用率，也能減少因人為操作失誤導(dǎo)致的安全事故發(fā)生。LIU等[1]提出了一種將領(lǐng)導(dǎo)-跟隨法與基于行為法相結(jié)合的過(guò)閘編隊(duì)控制系統(tǒng)，并設(shè)計(jì)了可切換的不同控制模式，利用實(shí)船平臺(tái)驗(yàn)證了該系統(tǒng)能夠提高船舶過(guò)閘安全性和效率；胡亞安等[3]通過(guò)在三峽船閘對(duì)4.5 m吃水船舶進(jìn)行同步移舶過(guò)閘試驗(yàn)，得出停泊安全是制約船閘通過(guò)能力的主要因素的結(jié)論；張勃等[2]對(duì)葛洲壩船閘船舶出閘運(yùn)動(dòng)進(jìn)行了研究，提出了“全同步出閘”和“半同步出閘”方式，驗(yàn)證了同步出閘可以縮短船舶出閘時(shí)間。

船舶在閘室水域內(nèi)的停船運(yùn)動(dòng)可歸結(jié)為直航減速運(yùn)動(dòng)，船舶列隊(duì)停船運(yùn)動(dòng)可歸結(jié)為直航協(xié)同運(yùn)動(dòng)。目前對(duì)直行協(xié)同運(yùn)動(dòng)的研究以車(chē)輛的自適應(yīng)巡航控制系統(tǒng)最為典型，該系統(tǒng)在車(chē)輛領(lǐng)域已經(jīng)能夠成熟地應(yīng)用。謝輝等[4]利用模型預(yù)測(cè)控制(model predictive control，MPC)算法設(shè)計(jì)了兩層控制器，分別用來(lái)計(jì)算期望加速度和協(xié)調(diào)驅(qū)動(dòng)與制動(dòng)，實(shí)現(xiàn)了無(wú)人駕駛車(chē)輛的橫縱向運(yùn)動(dòng)控制；孫濤等[5]針對(duì)交通燈場(chǎng)景下的車(chē)輛協(xié)同自適應(yīng)巡航控制問(wèn)題，利用MPC算法設(shè)計(jì)了可切換的控制器，提高了舒適性和燃油經(jīng)濟(jì)性。在航行器控制方面，李振福等[6]針對(duì)北極冰區(qū)航行環(huán)境，研究了船舶跟航模式下北極冰區(qū)的船舶安全間距；干偉東等[7]針對(duì)通航隧洞中的船舶跟馳問(wèn)題，提出了一種船舶跟馳安全間距計(jì)算方法，發(fā)現(xiàn)其安全間距與船舶所處位置有關(guān)；吳文祥等[8]設(shè)計(jì)了基于MPC的船舶直航協(xié)同控制方法，能夠?qū)崿F(xiàn)對(duì)預(yù)定變加速度目標(biāo)船的跟隨。利用MPC算法解決非線性系統(tǒng)及多約束問(wèn)題的獨(dú)特優(yōu)勢(shì)，可完成對(duì)單體船舶運(yùn)動(dòng)及多船舶編隊(duì)航行的有效控制[9]。但現(xiàn)有研究中針對(duì)閘室停船行為進(jìn)行描述的報(bào)道較少，且對(duì)閘室內(nèi)船舶協(xié)同停船的整體性考慮不足[10]。

本文在建立閘室水域船舶列隊(duì)直航運(yùn)動(dòng)模型的基礎(chǔ)上，采用速度-時(shí)間法和速度-位移法兩種方法設(shè)定參考速度，完成單船停船動(dòng)作MPC控制器設(shè)計(jì)，并在領(lǐng)航船按照上述兩種方法完成停船的前提下，加入跟隨船運(yùn)動(dòng)，設(shè)計(jì)三船協(xié)同停船運(yùn)動(dòng)MPC控制器，最后對(duì)停船控制的有效性進(jìn)行了仿真驗(yàn)證。

1 閘室水域船舶列隊(duì)直航運(yùn)動(dòng)模型

1.1 船閘場(chǎng)景描述

船閘水域通常包括引航道水域和閘室水域，如圖1所示。過(guò)閘航行的船舶一般會(huì)經(jīng)過(guò)引航道航行、進(jìn)閘航行、停船系泊、閘間移泊、出閘航行等階段。引航道是連接主航道和閘室的過(guò)渡性航道，保證船舶安全進(jìn)入閘室。閘室水域是指上下閘首和兩側(cè)閘壁圍成的空間。閘壁上設(shè)有浮式系船柱，供船舶在閘室內(nèi)停泊系纜。在閘室內(nèi)設(shè)有禁停線，所有船舶不能越過(guò)禁停線停船。

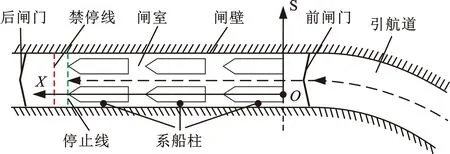
圖1 船閘示意圖Fig.1 Lock diagram

為更清楚地描述閘室內(nèi)船舶運(yùn)動(dòng)，以列隊(duì)中尾船的船尾位置為坐標(biāo)零點(diǎn)，以N-S坐標(biāo)系中正北方向作為入閘方向，并以入閘方向?yàn)榇爸焙竭\(yùn)動(dòng)坐標(biāo)正方向建立坐標(biāo)軸X。

1.2 船舶三自由度運(yùn)動(dòng)模型

船舶運(yùn)動(dòng)需6個(gè)自由度描述，即前進(jìn)、橫漂和起伏用來(lái)描述船舶的位置信息，首搖、橫搖和縱搖用來(lái)描述船舶的運(yùn)動(dòng)速度信息[11]。一般研究船舶軌跡或路徑運(yùn)動(dòng)問(wèn)題時(shí)，僅使用前進(jìn)、橫漂和首搖三自由度模型描述如下：

(1)

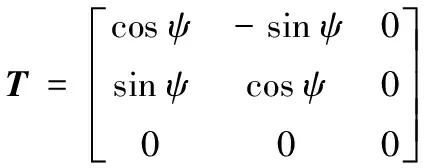
c23=m11uc31=m22v+0.5(m23+m32)

其中，x=(x,y,φ)T表示慣性坐標(biāo)系下船舶的位置和方向；v=(vu,vv，vr)T表示隨體坐標(biāo)系下船舶的速度和角速度；τc=(τu，τd，τr)T表示控制輸入的力和力矩；τD=(fdu,fdv，tdr)T表示干擾力和力矩；T表示坐標(biāo)變換矩陣，用于實(shí)現(xiàn)隨體坐標(biāo)系向慣性坐標(biāo)系的轉(zhuǎn)換；M表示慣性矩陣；C表示科氏向心矩陣；D表示阻尼矩陣。

將s(t)=(x,y,φ,vu,vv,vr)T設(shè)定為系統(tǒng)的狀態(tài)變量，u(t)=(τu，τd，τr)T設(shè)定為控制輸入，τD(t)=(fdu，fdv，tdr)T設(shè)定為干擾，則其狀態(tài)空間方程可表示為

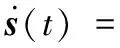
(2)

本文利用生成均勻分布的隨機(jī)數(shù)來(lái)設(shè)置干擾，表示為

(3)

式中，randi(·)為均勻分布的隨機(jī)整數(shù)；σ為權(quán)重參數(shù)。

1.3 船舶直航運(yùn)動(dòng)模型

1.3.1直航運(yùn)動(dòng)解耦

船舶列隊(duì)是指多艘船舶按照航行方向形成單向隊(duì)列，船舶三自由度模型是船舶平面運(yùn)動(dòng)的總體描述，針對(duì)閘室內(nèi)船舶直航列隊(duì)運(yùn)動(dòng)進(jìn)行研究，可以將三自由度模型進(jìn)行解耦，轉(zhuǎn)化為直航運(yùn)動(dòng)模型，本文利用解耦矩陣pi來(lái)完成。船舶直航運(yùn)動(dòng)模型坐標(biāo)關(guān)系見(jiàn)圖2。

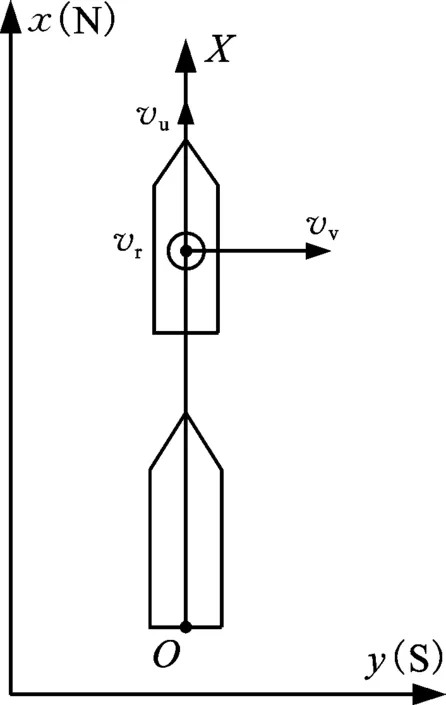
圖2 坐標(biāo)關(guān)系Fig.2 Coordinate relationship

狀態(tài)變量xl(t)設(shè)定為船舶直航方向坐標(biāo)位置和航行方向速度：

(4)

控制輸入變量ul(t)設(shè)定為船舶直航推進(jìn)力：

ul(t)=p2τc(t)=τu(t)

(5)

干擾量el(t)設(shè)定為直航運(yùn)動(dòng)方向上的干擾力：

el(t)=p2τD(t)=fdu(t)

(6)

則狀態(tài)空間方程變?yōu)橹焙竭\(yùn)動(dòng)狀態(tài)空間方程：

(7)

1.3.2模型線性化

針對(duì)非線性系統(tǒng)，可以直接利用非線性MPC求解最優(yōu)控制序列，但非線性求解過(guò)程復(fù)雜，不能保證實(shí)時(shí)性，而船閘航行環(huán)境對(duì)算法實(shí)時(shí)性要求高，故本文的仿真采用對(duì)模型線性化后求解最優(yōu)控制序列的方法。

假設(shè)參考系統(tǒng)給出的參考狀態(tài)量能夠完整完成目標(biāo)航行任務(wù)，在獲取航行路徑上每一時(shí)刻狀態(tài)量和控制量的基礎(chǔ)上，構(gòu)造真實(shí)狀態(tài)量與參考量的偏差，利用偏差設(shè)計(jì)控制器完成目標(biāo)航行任務(wù)。參考量方程表示為

(8)

對(duì)船舶航行任意時(shí)刻的直航運(yùn)動(dòng)狀態(tài)空間方程在參考點(diǎn)處進(jìn)行一階泰勒展開(kāi)，去掉高階項(xiàng)并代入?yún)⒖枷到y(tǒng)，得

(9)

將式(9)與式(8)相減得到需要的偏差表達(dá)式：

(10)

1.3.3模型離散化

采用近似離散化方法對(duì)狀態(tài)空間方程進(jìn)行離散化處理，近似離散化方法計(jì)算公式為

(11)

式中，Ts為離散化步長(zhǎng)；Adis、Bdis分別為離散化后的狀態(tài)矩陣和輸入變量。

離散化后的狀態(tài)空間方程可用作預(yù)測(cè)模型，表示為

(12)

1.4 船舶列隊(duì)間距模型

建立3艘船舶列隊(duì)航行的間距模型，其狀態(tài)變量xh(t)和控制變量uh(t)設(shè)定見(jiàn)下式：

(13)

式中，d1(t)、d2(t)分別為首船與中間船、中間船與尾船的船間距。

根據(jù)協(xié)同入閘船舶的直航運(yùn)動(dòng)關(guān)系，建立入閘船隊(duì)運(yùn)動(dòng)的狀態(tài)空間方程：

(14)

式中，xli(t)為入閘船隊(duì)中第i艘船舶的直航運(yùn)動(dòng)狀態(tài)變量。

為提高控制實(shí)時(shí)性，采用歐拉法進(jìn)行離散化。根據(jù)編隊(duì)運(yùn)動(dòng)關(guān)系，將式(14)離散化后可以得到入閘停船控制系統(tǒng)船間距模型的離散狀態(tài)方程：

(15)

領(lǐng)航船在完成單船控制時(shí)的控制誤差會(huì)對(duì)上層控制器帶來(lái)不必要的計(jì)算量，并且影響上層控制器對(duì)跟隨船的控制效果。為了削弱這種影響，將領(lǐng)航船的真實(shí)航速與參考航速按照一定權(quán)重混合后作為上層控制器的輸入值：

vint(t)=γvref(t)+(1-γ)v1(t)

(16)

式中，γ為權(quán)值。

式(15)可變?yōu)?/p>

(17)

綜上所述，船舶列隊(duì)運(yùn)動(dòng)模型的建立過(guò)程可用圖3表示。

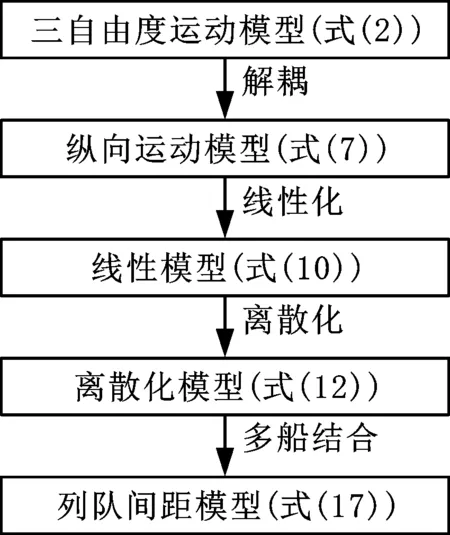
圖3 模型建立流程Fig.3 Model building process

2 單船停船模型預(yù)測(cè)控制器

模型預(yù)測(cè)控制采用滾動(dòng)優(yōu)化機(jī)制[6]，具有顯式處理約束的能力，算法利用預(yù)測(cè)能力可以解決系統(tǒng)誤差和不確定環(huán)境的參數(shù)等問(wèn)題，具有良好的魯棒性。

2.1 參考狀態(tài)設(shè)計(jì)

結(jié)合船舶直航運(yùn)動(dòng)模型的狀態(tài)量為控制系統(tǒng)設(shè)計(jì)參考狀態(tài)量xlref：

(18)

式中，xref(k)為位置參考量；vuref(k)為速度參考量。

本節(jié)采用速度-時(shí)間法和速度-位移法這兩種方法設(shè)置速度參考量。

2.1.1速度-時(shí)間法

速度-時(shí)間法是指在停船航行運(yùn)動(dòng)過(guò)程中，每一個(gè)時(shí)間對(duì)應(yīng)一個(gè)參考航速值。在停船動(dòng)作連續(xù)的情況下，按照停船時(shí)間進(jìn)行勻減速停船是一種保證船內(nèi)平順性和節(jié)能性的理想方法。但實(shí)際停船所用時(shí)間往往不能固定，故本文設(shè)定以0.5倍初速度勻速航行完成停船距離所用時(shí)間作為預(yù)設(shè)航行時(shí)間。仿真環(huán)境中，船舶運(yùn)動(dòng)的參考量設(shè)定為

(19)

式中，xaim為目標(biāo)停船坐標(biāo)；v0為初速度；as為設(shè)定加速度。

將參考量進(jìn)行離散化處理后得到每一控制時(shí)刻的參考量：

(20)

式中，Nref為參考時(shí)刻點(diǎn)的個(gè)數(shù)。

2.1.2速度-位移法

速度-位移法是指在停船航行位移線上，每一個(gè)位移值對(duì)應(yīng)一個(gè)參考航速值，參考值可按照到停船線距離勻減速設(shè)置。速度參考量設(shè)置可描述為

uref=v0-ρx

(21)

式中,ρ為勻變速常數(shù)，ρ=v0/xaim。

由于在實(shí)際停船過(guò)程中往往是通過(guò)停船線位置來(lái)衡量停船行為的，故將式(21)作差值形式轉(zhuǎn)換如下：

uref=ρ(xaim-x)

(22)

速度-位移法是更貼合駕駛員行為的一種停船方式，人們?cè)隈{駛時(shí)往往通過(guò)判斷與前方障礙物的距離選擇駕駛的制動(dòng)尺度，與前方障礙物距離越近，則使用越強(qiáng)的制動(dòng)力。

在仿真中，建立速度隨距停船線距離變化的函數(shù)，在預(yù)測(cè)步長(zhǎng)內(nèi)，取每一步的船舶位置信息，利用函數(shù)得到對(duì)應(yīng)的參考速度來(lái)構(gòu)成當(dāng)前時(shí)刻的速度參考矩陣。

2.2 目標(biāo)函數(shù)設(shè)計(jì)

結(jié)合式(4)、式(18)，構(gòu)造k時(shí)刻系統(tǒng)偏差量：

De(k)=xl(k)-xlref(k)

(23)

在預(yù)測(cè)時(shí)域中，以系統(tǒng)偏差量為控制目標(biāo)，設(shè)置一個(gè)加權(quán)形式的目標(biāo)函數(shù)來(lái)描述待優(yōu)化問(wèn)題：

(24)

式中，Jsing為單船入閘停船運(yùn)動(dòng)的目標(biāo)函數(shù)；Np為預(yù)測(cè)步長(zhǎng)；Nc為控制步長(zhǎng)；Q為權(quán)重矩陣；R為權(quán)值；Δu為控制量偏差(本文參考控制量取0)。

通過(guò)上述變化，單船入閘停船運(yùn)動(dòng)控制的優(yōu)化問(wèn)題就可描述為求解約束條件下使目標(biāo)函數(shù)Jsing值最小的控制量ul(k)。

考慮到船舶受動(dòng)力機(jī)構(gòu)機(jī)械性能的影響，對(duì)控制量和控制增量的約束設(shè)置如下：

ulmin(k+i)≤ul(k+i)≤ulmax(k+i)

Δulmin(k+i)≤Δul(k+i)≤Δulmax(k+i)

i=0，1，…，Nc

3 船舶列隊(duì)停船模型預(yù)測(cè)控制器

3.1 場(chǎng)景描述

以3艘船協(xié)同入閘停船航行為例，如圖4所示，經(jīng)過(guò)引航道后，船S1、S2、S3沿直線列隊(duì)入閘停船。An、Bn和Ln分別表示船Sn的船首、船尾位置和船長(zhǎng)(n=1，2，3)。在入閘任務(wù)的任意時(shí)刻k，船S1、S2、S3的航速分別表示為Vu1(k)、Vu2(k)和Vu3(k)。船S1、S2的間距B1A2為d1(k)，船S2、S3的間距B2A3為d2(k)。

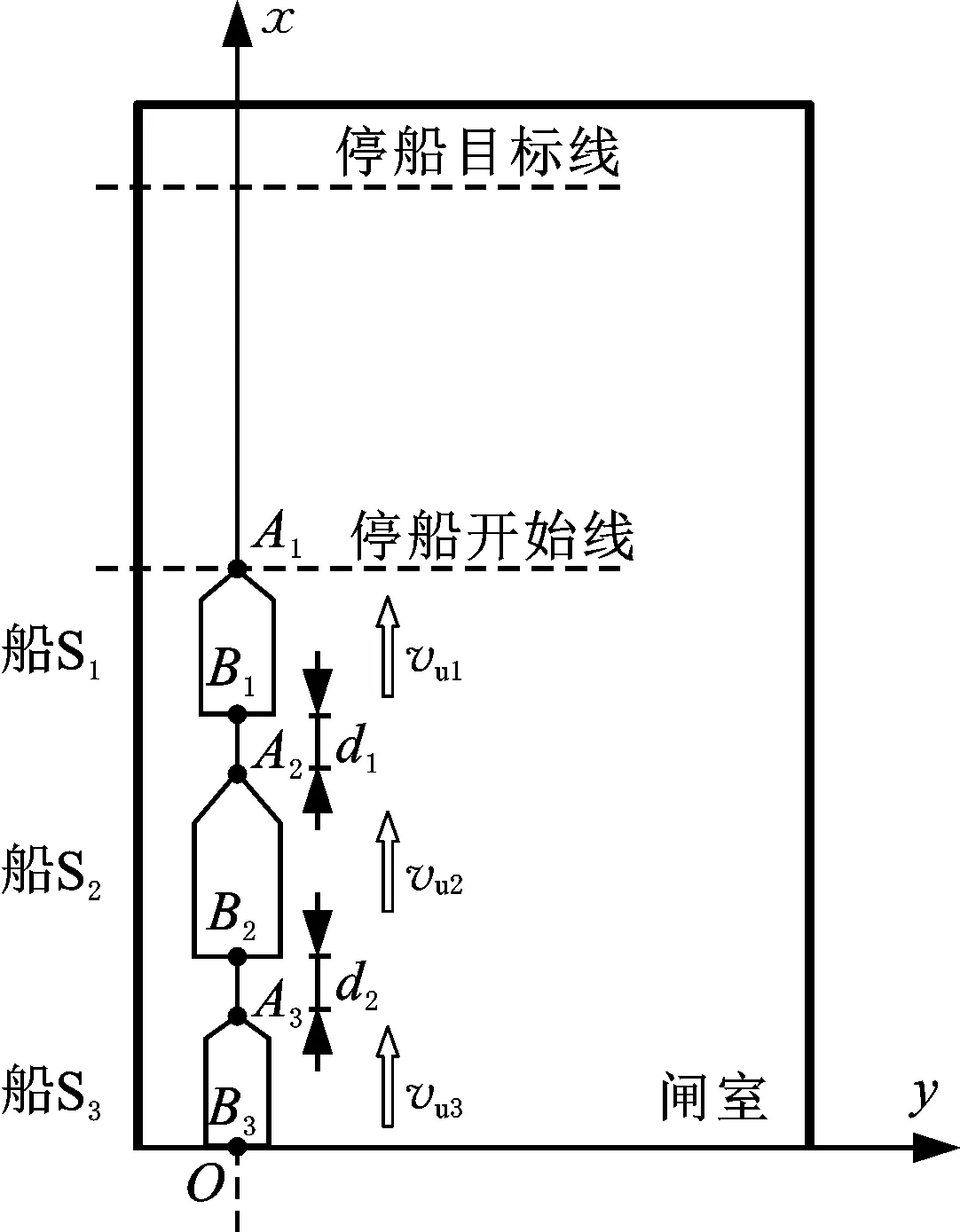
圖4 協(xié)同入閘場(chǎng)景示意Fig.4 Synergistic gate entry scene

3艘船列隊(duì)入閘，它們分別要完成直線入閘停船的任務(wù)。在協(xié)同入閘場(chǎng)景下，船舶間距小，航行操縱頻繁，控制器既要完成每艘船的停船任務(wù)，又要保持動(dòng)態(tài)船間距，保證航行安全性。

將單船運(yùn)動(dòng)仿真中的船舶位置定義為船首位置，結(jié)合船長(zhǎng)可得到船間距：

(25)

3.2 控制器設(shè)計(jì)

如圖5所示，協(xié)同入閘系統(tǒng)的控制器設(shè)計(jì)分為上層控制器和下層控制器。

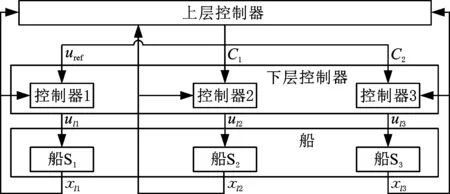
圖5 列隊(duì)停船控制器結(jié)構(gòu)Fig.5 Ship platoon parking control structure

上層控制器是集中控制器，用于計(jì)算船舶列隊(duì)的協(xié)同控制信息。對(duì)于船閘水域，集中式上層控制器可以被看作岸基對(duì)入閘船舶的集中調(diào)配。集中式控制器是指由一個(gè)控制器求解整個(gè)系統(tǒng)的優(yōu)化問(wèn)題，將輸出量發(fā)送給各子系統(tǒng)。與分散式和分布式控制器相比，集中式控制器得到的控制輸出和系統(tǒng)性能都是最優(yōu)的，但對(duì)集中控制器的依賴(lài)較強(qiáng)且控制器的計(jì)算負(fù)擔(dān)較重。

岸基上層控制器接收各入閘船舶發(fā)送的當(dāng)前位置、速度，根據(jù)式(25)計(jì)算得到船間距，代入船間距模型中得到預(yù)測(cè)時(shí)域內(nèi)船間距預(yù)測(cè)值，進(jìn)而計(jì)算出各船舶的期望速度向量并傳遞給各船舶的下層控制器。

下層控制器的設(shè)計(jì)采用單船停船模型預(yù)測(cè)控制器，下層控制器將上層控制器的控制輸出量作為下層控制器的參考量，計(jì)算得到所需的推力ul并作為輸出量傳遞到船舶，船舶執(zhí)行后將新的位置、速度等信息反饋到上、下層控制器中。

3.3 上層控制器目標(biāo)函數(shù)設(shè)計(jì)

船舶列隊(duì)入閘控制的控制目標(biāo)為保持期望船間距并精準(zhǔn)停船。其中，精準(zhǔn)停船問(wèn)題可利用領(lǐng)航船的下層控制器完成，上層控制器則負(fù)責(zé)保持期望船間距，因此，在預(yù)測(cè)時(shí)域中，上層控制器的目標(biāo)函數(shù)設(shè)計(jì)如下：

(26)

式中，Jglob為協(xié)同控制的目標(biāo)函數(shù)；H、K為權(quán)重矩陣；Npt為上層控制器的預(yù)測(cè)步長(zhǎng)；Nct為上層控制器的控制步長(zhǎng)；C為上層控制器輸出控制量。

第p個(gè)船間距與設(shè)定船間距之差Δdp為

Δdp=dp-dpaim

式中，dp為船間距的真實(shí)值，可由式(25)得到；dpaim為船間距的目標(biāo)值。

船舶列隊(duì)入閘停船運(yùn)動(dòng)控制的優(yōu)化問(wèn)題可描述為求解約束條件下使目標(biāo)函數(shù)Jglob值最小的控制向量C(t)，即每艘入閘船舶的下層控制器提供參考速度。

考慮到每艘船舶的動(dòng)力機(jī)構(gòu)機(jī)械性能的不同，按照第2節(jié)中停船方式航行的要求，對(duì)于各船舶控制量和控制增量的約束設(shè)置如下：

Cmin(k+i)≤C(k+i)≤Cmax(k+i)

ΔCmin(k+i)≤ΔC(k+i)≤ΔCmax(k+i)

i=0，1，…，Nc-1

4 仿真實(shí)驗(yàn)

4.1 仿真模型

本文選擇一艘3500 t油化船實(shí)船作為研究對(duì)象，船長(zhǎng)為94.6 m，船寬為17.2 m，設(shè)計(jì)吃水深度為5 m，螺旋槳在最大轉(zhuǎn)速下的推力為180 kN。該模型對(duì)應(yīng)的系統(tǒng)參數(shù)為

m11=mrb+ma=5990 929+297 670=6288 590(kg)

式中，mrb為船舶直航質(zhì)量；ma為直航附加質(zhì)量。

d11采用經(jīng)驗(yàn)公式擬合的方法，其大小隨航速變化，變化關(guān)系如圖6所示。

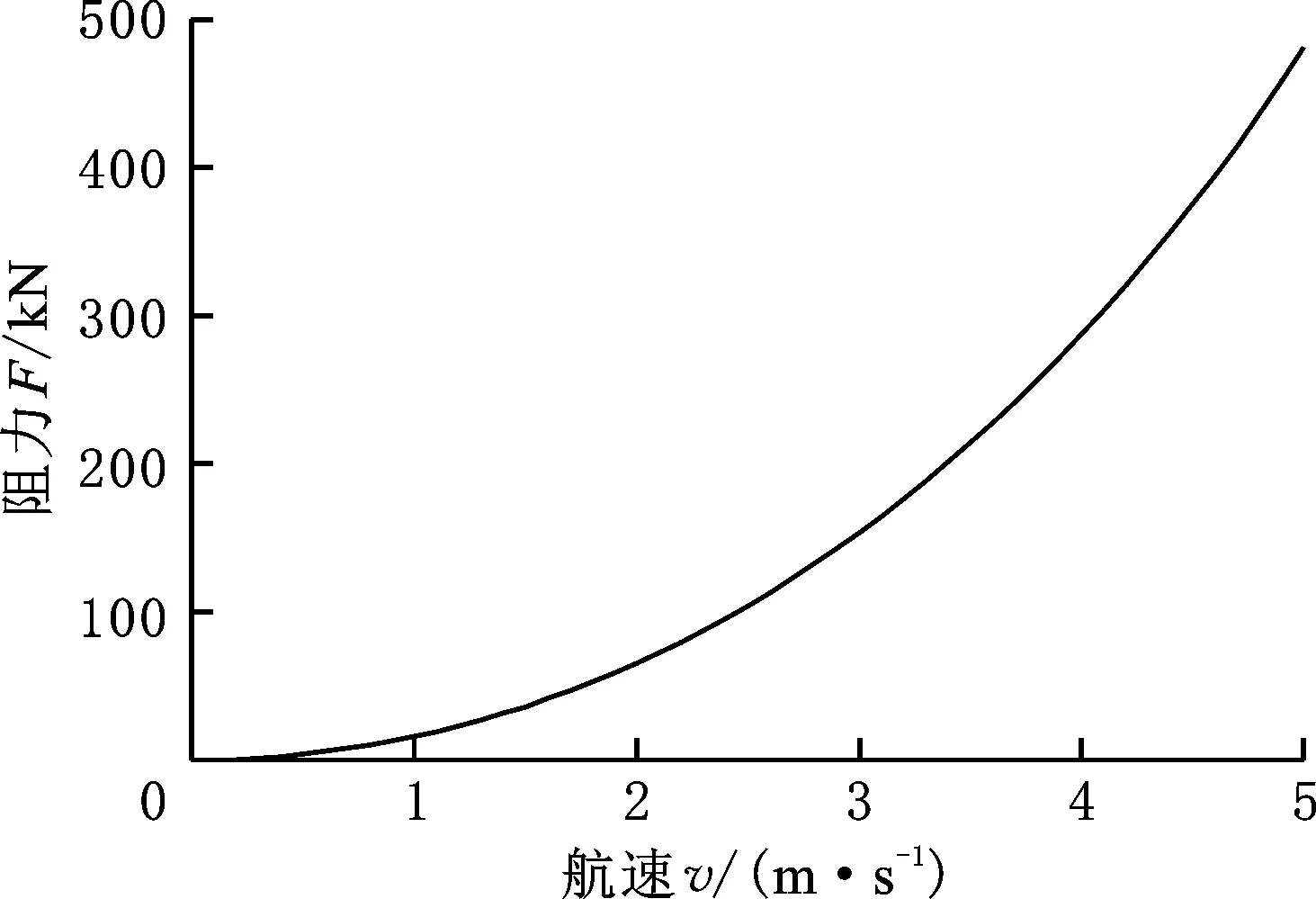
圖6 阻力曲線Fig.6 Resistance curve

4.2 單船停船控制仿真實(shí)驗(yàn)

4.2.1最短停船距離計(jì)算

采用MATLAB軟件對(duì)本文控制方法進(jìn)行仿真驗(yàn)證。為保證停船的安全性，首先驗(yàn)證在最大制動(dòng)力下不同初速度v0船舶的最短停船距離dmin，在所選船型實(shí)際航行過(guò)程中，螺旋槳產(chǎn)生的推進(jìn)或制動(dòng)力一般滿(mǎn)足區(qū)間-180 kN<τu<180 kN，故在不同初速度下給定τu=-180 kN進(jìn)行實(shí)驗(yàn)，初速度在0～1.5 m/s間每隔0.05 m/s取一個(gè)樣本點(diǎn)，取Ts=2 s，得到30組初速度-最短停船距離的關(guān)系，然后用五次函數(shù)進(jìn)行函數(shù)擬合，得到的函數(shù)關(guān)系如下：

(27)

其函數(shù)圖像如圖7所示。根據(jù)該函數(shù)可計(jì)算出在不同初速度下船舶完成停船的安全距離，函數(shù)平均擬合誤差為0.0161 m。利用兩種參考速度的設(shè)置方法對(duì)初速度為1 m/s的模型船入閘停船行為進(jìn)行仿真，給定停船距離為290 m。

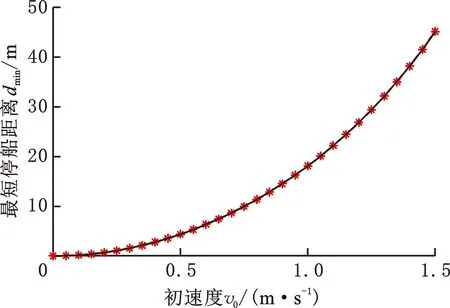
圖7 船舶初速度-最短停船距離關(guān)系Fig.7 The relationship between initial speed and minimum stopping distance

4.2.2速度-時(shí)間法

根據(jù)1 m/s初速度，本次仿真時(shí)間預(yù)設(shè)為580 s。離散化后的參考量設(shè)定為

(28)

式中，Nref取290。

目標(biāo)函數(shù)中權(quán)重矩陣及權(quán)值分別設(shè)置為

R1=1.5×10-11

船舶動(dòng)力機(jī)構(gòu)約束設(shè)置為

-180 kN≤ul(k+i)≤180 kN

-30 kN≤Δul(k+i)≤30 kN

i=0，1，…，Nc-1

控制器的控制步數(shù)和預(yù)測(cè)步數(shù)設(shè)置為

Nc=Np=6

干擾大小設(shè)置為

τD∈[-3，3] kN

仿真運(yùn)行后得到的距離、速度和控制器輸入結(jié)果分別如圖8 ～圖10所示。

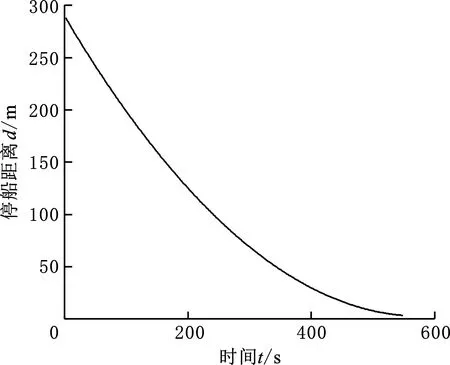
圖8 停船過(guò)程中距離動(dòng)態(tài)變化(速度-時(shí)間法)Fig.8 Dynamic change of distance during stopping(speed-time method)

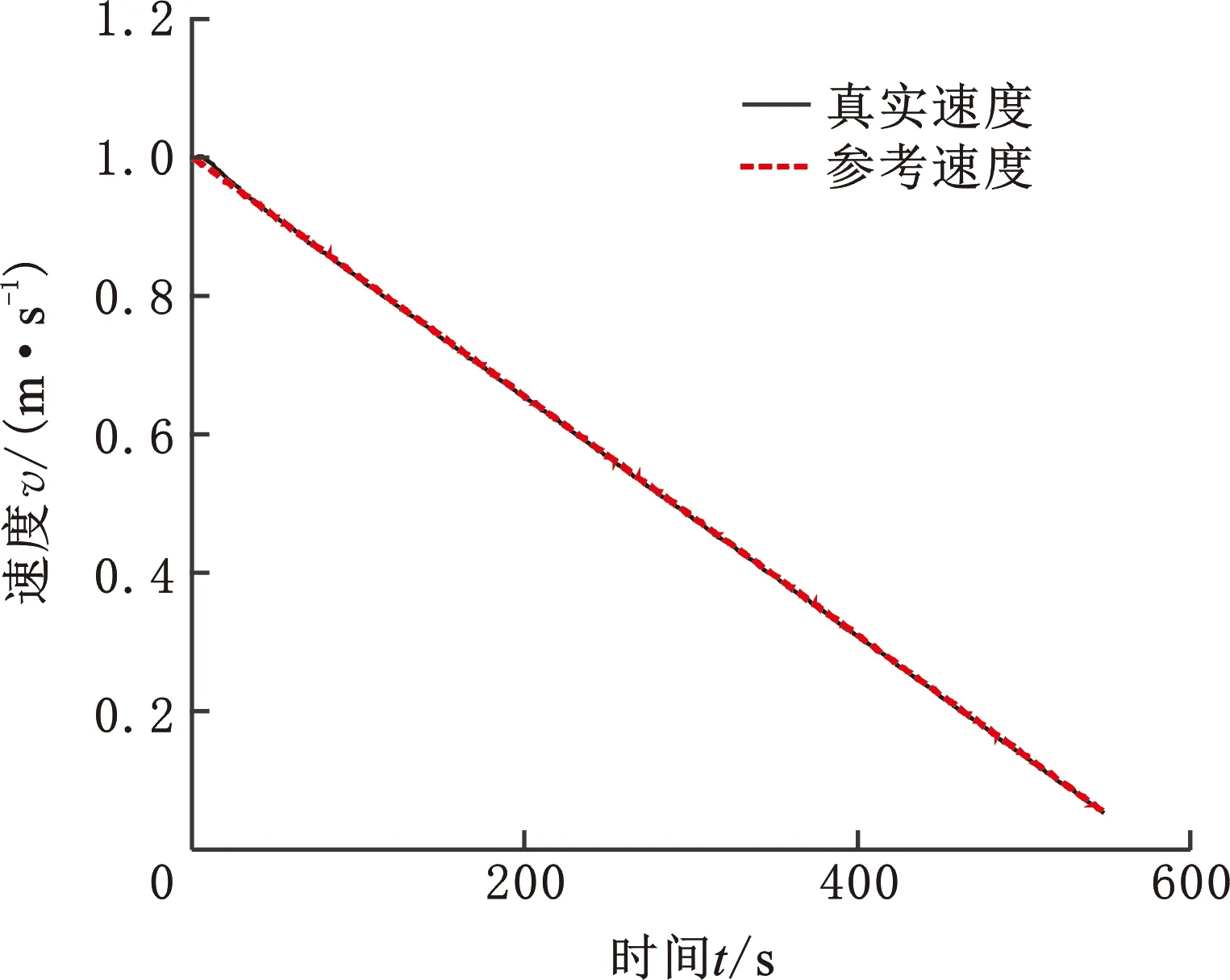
圖9 停船過(guò)程中速度動(dòng)態(tài)變化(速度-時(shí)間法)Fig.9 Dynamic change of velocity during stopping(speed-time method)

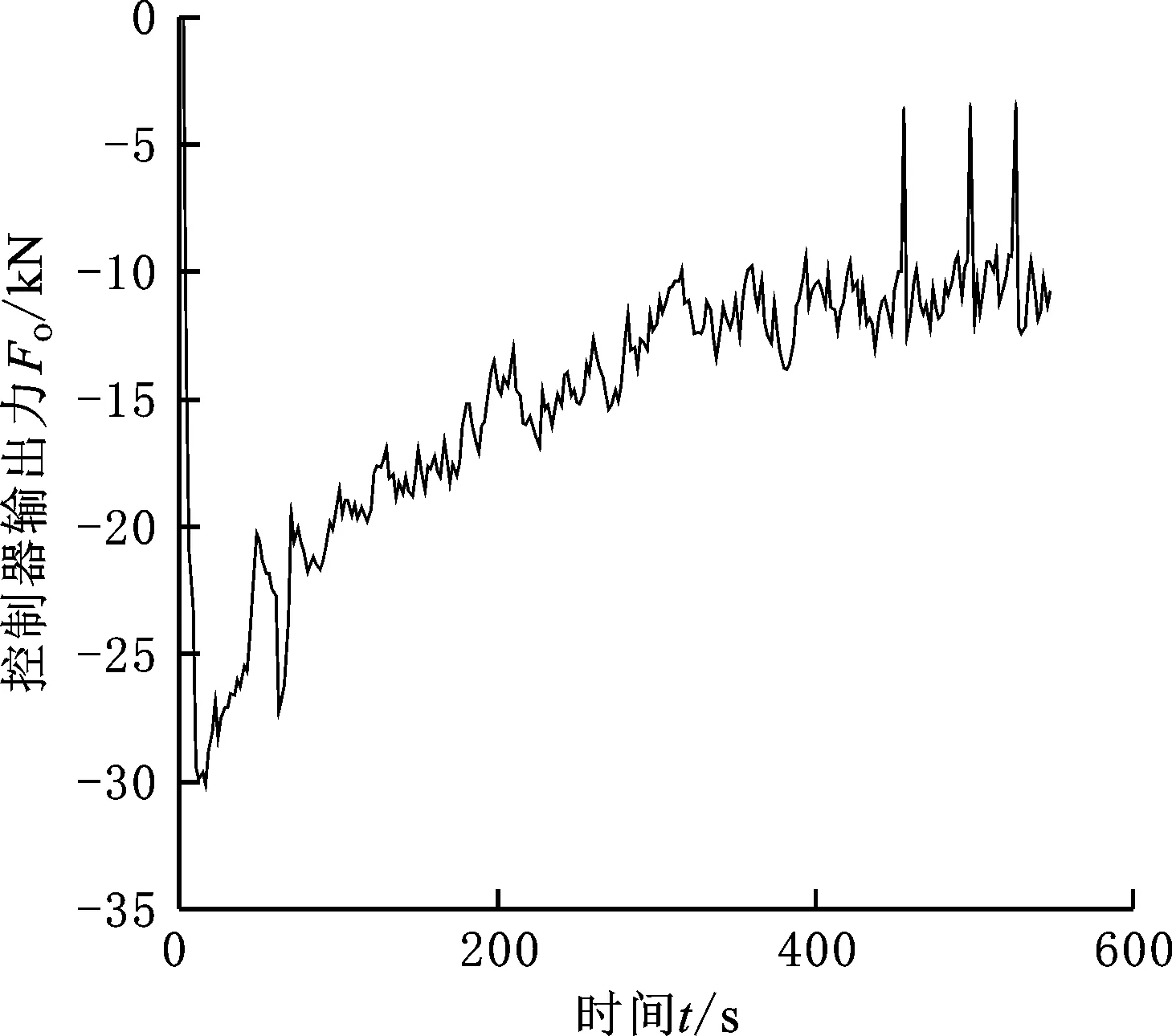
圖10 停船過(guò)程中控制器輸出力(速度-時(shí)間法)Fig.10 Control output force during stopping(speed-time method)

設(shè)定船舶航速小于0.05 m/s時(shí)即認(rèn)為停船任務(wù)完成，本次仿真實(shí)驗(yàn)完成停船共用時(shí)572 s，航行距離為286.51 m。

由圖8可以看出，由于初期速度較大，船舶到停船線的距離減小的速度較快，距離小于50 m后，減小速度趨于平穩(wěn)，最終能較為準(zhǔn)確地停在停船線之前。由圖9可以看出，仿真30 s前，由于初始控制量為0，輸出推力與阻力的合力暫時(shí)難以為船舶提供指定的負(fù)加速度值，且位置距停船線較遠(yuǎn)，距離差數(shù)值較大，所以在目標(biāo)函數(shù)的值中，距離差所占比重大。此時(shí)為了到達(dá)目標(biāo)位置，船舶在短時(shí)間內(nèi)保持初速度甚至稍有加速航行，同時(shí)輸出控制力迅速變化，距離隨之迅速減小，參考速度在目標(biāo)函數(shù)中的權(quán)重開(kāi)始變大，速度曲線逐漸與參考速度曲線重合。結(jié)合圖10，仿真進(jìn)行20 s時(shí)，控制器預(yù)測(cè)到船舶受力達(dá)到期望加速度要求，便不再提供更大的負(fù)推力，控制量輸出變化早于速度變化，可體現(xiàn)出預(yù)測(cè)控制的優(yōu)勢(shì)。由圖10可以看出，控制器輸出力在面對(duì)隨機(jī)干擾時(shí)能夠做出積極的響應(yīng)，具有良好的魯棒性，但在仿真300 s后有一定的短時(shí)波動(dòng)。

4.2.3速度-位移法

將速度-時(shí)間法中生成的干擾向量應(yīng)用到速度-位移仿真當(dāng)中，其余仿真參數(shù)均與速度-時(shí)間法相同。得到的仿真結(jié)果如圖11～圖14所示。同理，設(shè)定船舶航速小于0.05 m/s時(shí)即認(rèn)為停船任務(wù)完成，本次仿真實(shí)驗(yàn)完成停船共用時(shí)860 s，航行距離為276.16 m。

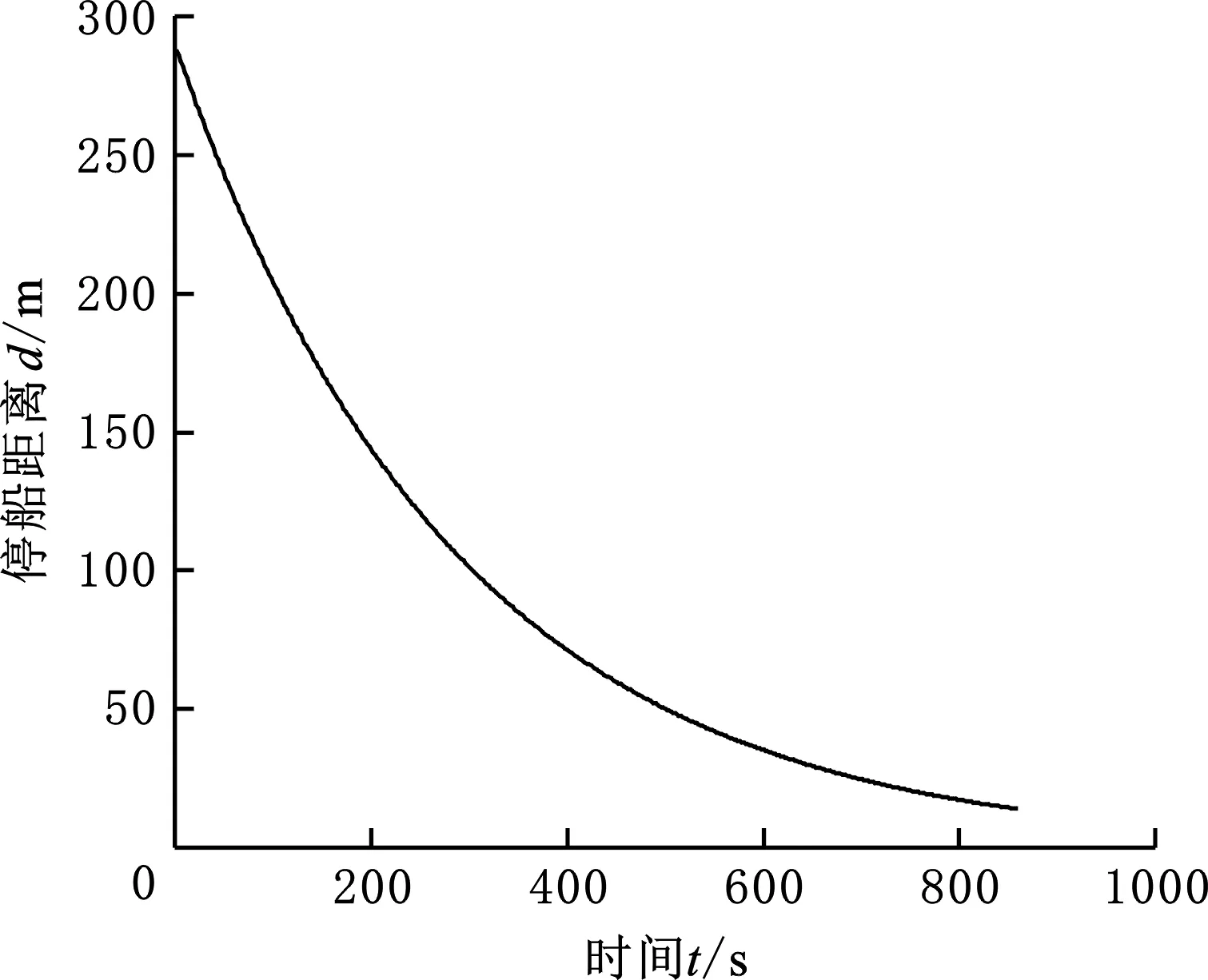
圖11 停船過(guò)程中距離動(dòng)態(tài)變化(速度-位移法)Fig.11 Dynamic change of distance during stopping(speed-displacement method)

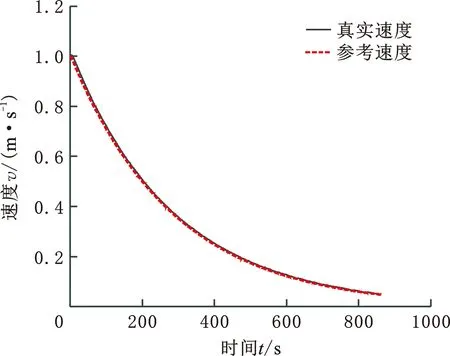
圖12 停船過(guò)程中速度動(dòng)態(tài)變化(速度-位移法)Fig.12 Dynamic change of velocity during stopping(speed-displacement method)

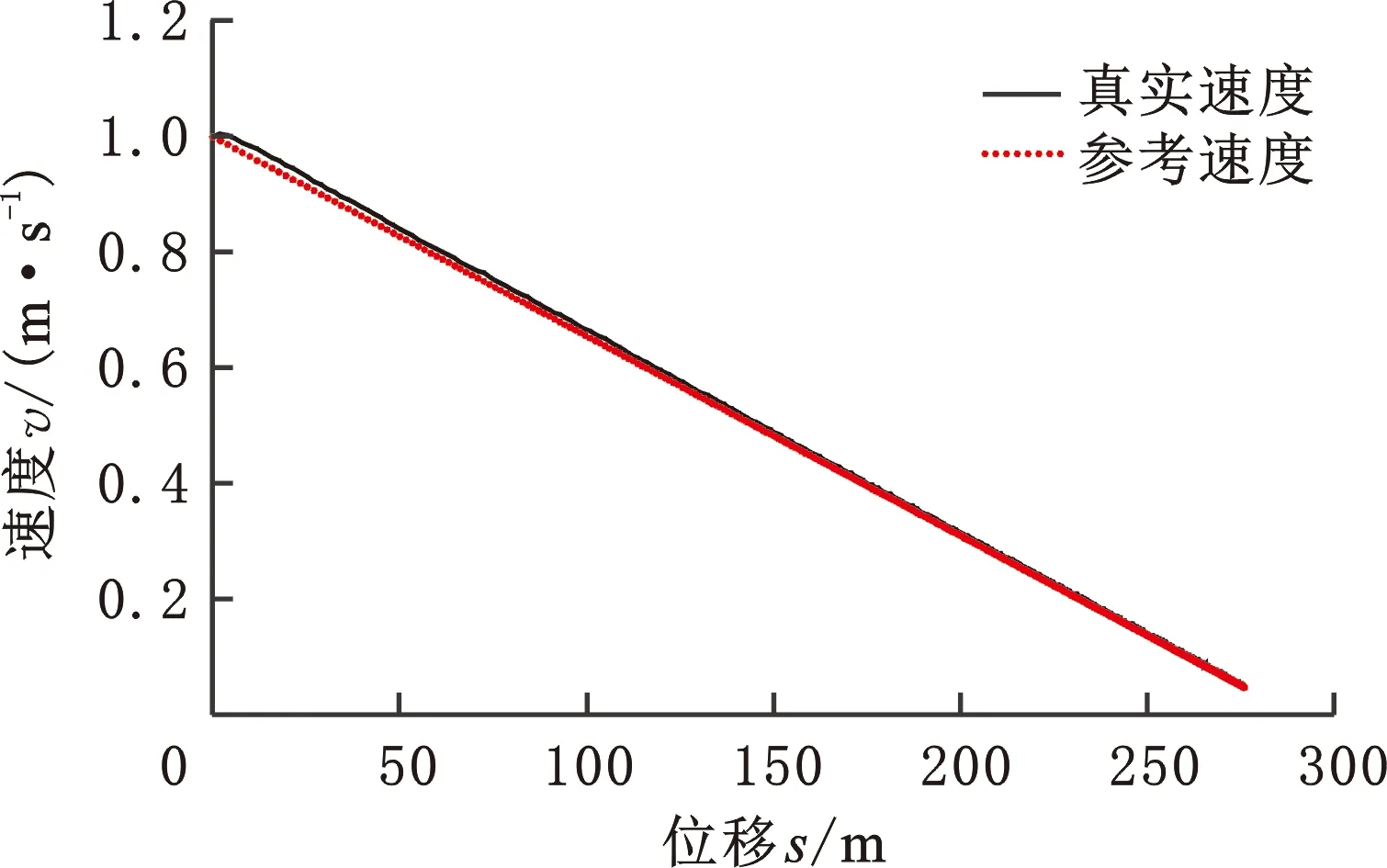
圖13 停船過(guò)程中速度隨位移變化(速度-位移法)Fig.13 The velocity varies with displacement during stopping (speed-displacement method)

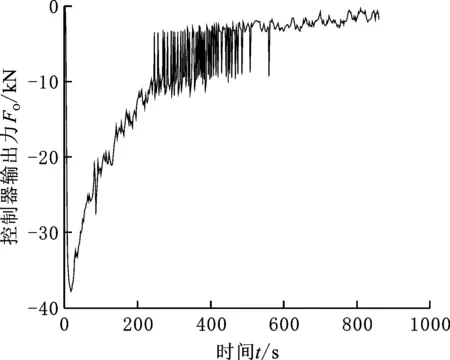
圖14 停船過(guò)程中控制器輸出力(速度-位移法)Fig.14 Control output force during stopping(speed-displacement method)

由圖11可以看出，相比圖8的距離變化過(guò)程，采用速度-位移法減速整體距離變化較為平緩，500 s后船舶才到達(dá)距離停船線50 m處，且最終的停船位置距停船線更遠(yuǎn)。由圖12和圖13可以看出，與速度-時(shí)間法仿真類(lèi)似，采用速度-位移法的初期同樣有一段時(shí)間的速度增加，之后速度隨時(shí)間有一段迅速下降過(guò)程，速度小于0.3 m/s后減速過(guò)程趨于平緩。距離停船線140 m以?xún)?nèi)，船舶幾乎隨到停船線距離的減小做勻減速運(yùn)動(dòng)，并在停船運(yùn)動(dòng)中后期與參考速度曲線重合。圖14反映了停船過(guò)程中控制器輸出制動(dòng)力的變化，在運(yùn)動(dòng)初期的一段時(shí)間內(nèi)，系統(tǒng)提供了較大的負(fù)推力使船舶達(dá)到當(dāng)前航速的動(dòng)態(tài)平衡，平衡狀態(tài)在25 s時(shí)進(jìn)入控制器預(yù)測(cè)時(shí)域，并在35 s時(shí)達(dá)到平衡。仿真進(jìn)行到256 s時(shí)，控制器輸出出現(xiàn)一定波動(dòng)，并在478 s后恢復(fù)平穩(wěn)，最終控制器輸出趨近于零。相比速度-時(shí)間法，速度位移法在仿真結(jié)束時(shí)的控制量較小，具有更好的應(yīng)變能力。

4.2.4結(jié)果對(duì)比分析

以航行經(jīng)濟(jì)性、平順性及船閘效率作為評(píng)價(jià)標(biāo)準(zhǔn)，設(shè)計(jì)評(píng)價(jià)指標(biāo)來(lái)衡量停船控制效果。經(jīng)濟(jì)性可通過(guò)停船運(yùn)動(dòng)消耗能量來(lái)表示，平順性可通過(guò)最大加速度和加速度方差來(lái)表示，船閘效率用閘室單次運(yùn)行時(shí)間來(lái)表示：

(29)

式中，WS為運(yùn)動(dòng)耗能指標(biāo)；WC為航行平順性指標(biāo)；T為運(yùn)動(dòng)總用時(shí)；It為仿真總步數(shù)；amax、as分別為加速度的最大值和平均值。

用上述變量構(gòu)造評(píng)價(jià)指標(biāo)：

KP=(μ1WS+μ2WC)(T+Tg)

(30)

式中，KP為評(píng)價(jià)指標(biāo)；Tg為船閘停船間歇時(shí)間；μ1、μ2為權(quán)值。

取μ1=0.6，μ2=80，Tg=300 s。單船停船運(yùn)動(dòng)仿真中兩種速度控制方式的運(yùn)動(dòng)評(píng)價(jià)見(jiàn)表1。

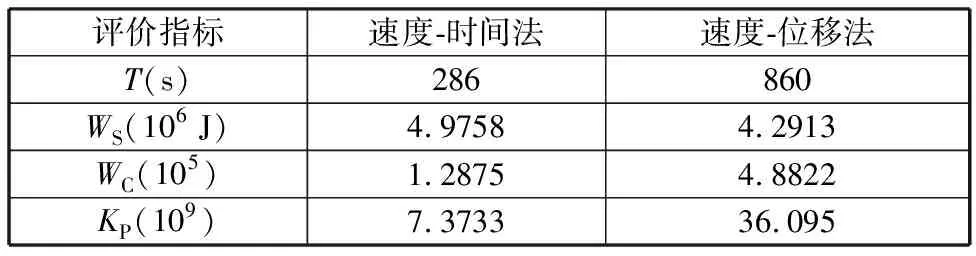
表1 單船停船運(yùn)動(dòng)評(píng)價(jià)指標(biāo)Tab.1 Single ship stopping motion evaluation index

評(píng)價(jià)指標(biāo)對(duì)應(yīng)數(shù)值越小表示該方法在該指標(biāo)下表現(xiàn)越好，由評(píng)價(jià)指標(biāo)數(shù)值的對(duì)比看出，速度-時(shí)間法在船舶的航行時(shí)間和平順性上具有明顯優(yōu)勢(shì)；在經(jīng)濟(jì)性方面，速度-位移法具有優(yōu)勢(shì)。結(jié)合整個(gè)船閘通航效率而言，速度-時(shí)間法可以做到更短的過(guò)閘航行周期，優(yōu)勢(shì)明顯。

速度-位移法的優(yōu)勢(shì)在于停船任務(wù)末期，船舶航速變化已經(jīng)很小，且推力也趨近于0，這樣比較容易控制停船線附近的船舶行為，有利于船舶航行安全性。

4.3 船舶列隊(duì)停船控制仿真實(shí)驗(yàn)

仿真工況如下：3艘船舶列隊(duì)入閘完成停船運(yùn)動(dòng)，開(kāi)始停船前各船的初速度均為1 m/s，且初始船間距為5 m，領(lǐng)航船在距停船線290 m處開(kāi)始停船，設(shè)定目標(biāo)船間距為5 m，后船在上層控制器的控制下跟隨領(lǐng)航船完成停船。

上層控制器目標(biāo)函數(shù)中的權(quán)值及權(quán)重矩陣設(shè)置如下：

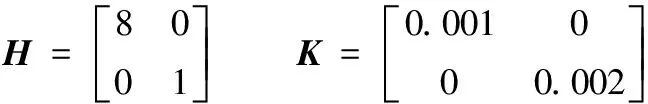
參考權(quán)值γ=0.3。上層控制器的仿真約束設(shè)置為

(0,0)T≤C(k+i)≤(1.5,1.5)Tm/s

(-0.06,-0.06)Tm/s≤ΔC(k+i)≤

(0.06,0.06)Tm/s

i=0，1，…，Nc-1

為了既保證領(lǐng)航船控制停船位置，又跟隨船更好地執(zhí)行上層控制器指令，三艘船的下層控制器中權(quán)重矩陣及權(quán)值設(shè)置分別為

R1=R2=R3=1.5×10-11

用船舶慣性矩陣差異來(lái)表示船舶裝載量差異，用控制器輸出增量約束差異表現(xiàn)動(dòng)力機(jī)構(gòu)差異。則三艘船的慣性矩陣和仿真約束分別設(shè)置為

m11-S1=6288 590 kg

m11-S2=5388 590 kg

m11-S3=5788 590 kg

i=0，1，…，Nc-1

領(lǐng)航船按照速度-時(shí)間法完成停船得到的仿真結(jié)果如圖15～圖18所示。

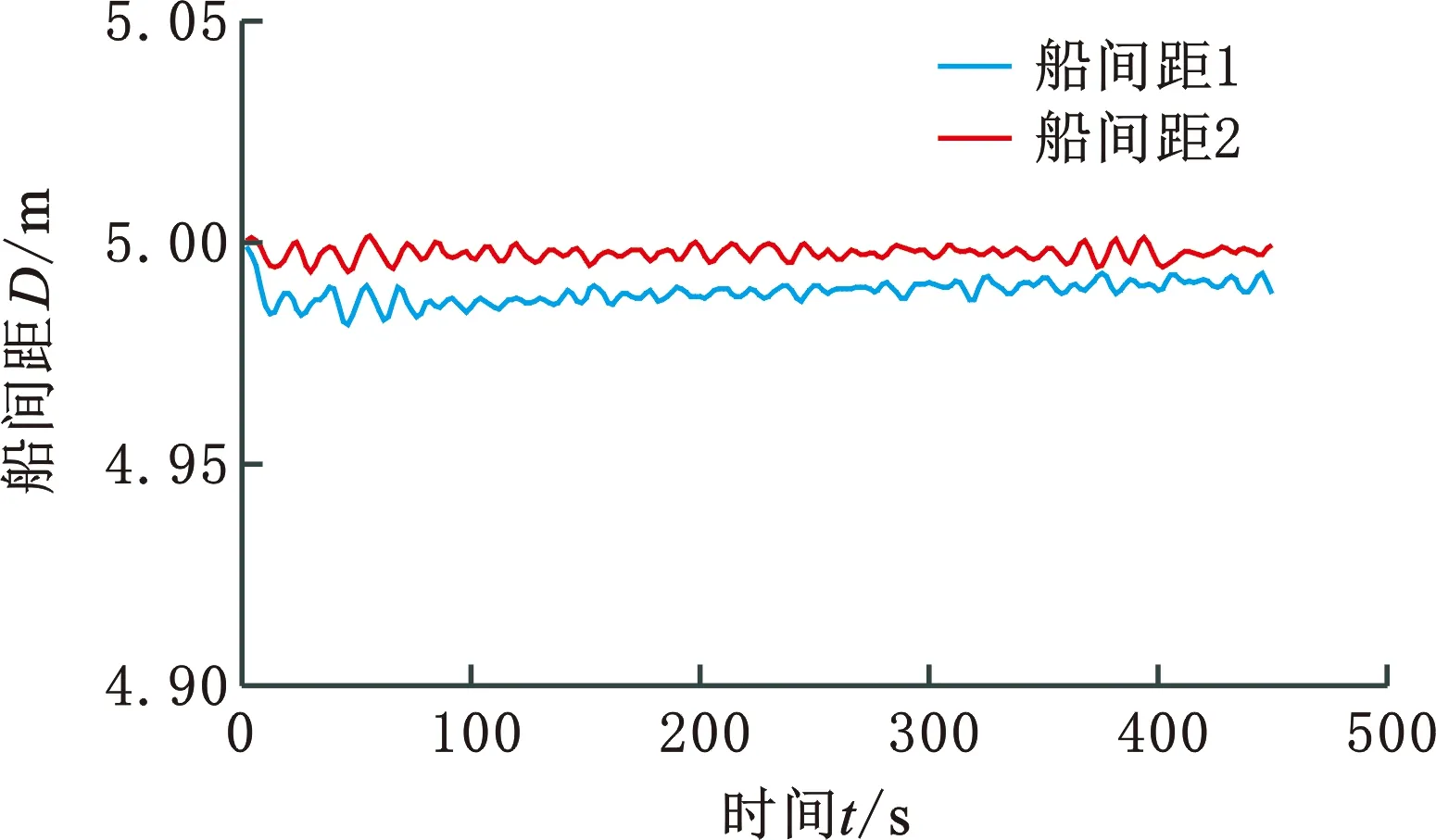
圖15 船間距動(dòng)態(tài)變化(速度-時(shí)間法)Fig.15 Dynamic change of ship spacing(speed-time method)

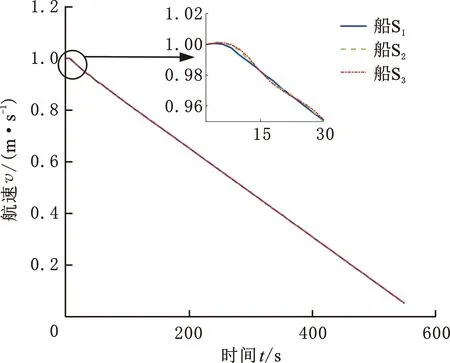
圖16 航速動(dòng)態(tài)變化(速度-時(shí)間法)Fig.16 Dynamic change of speed(speed-time method)

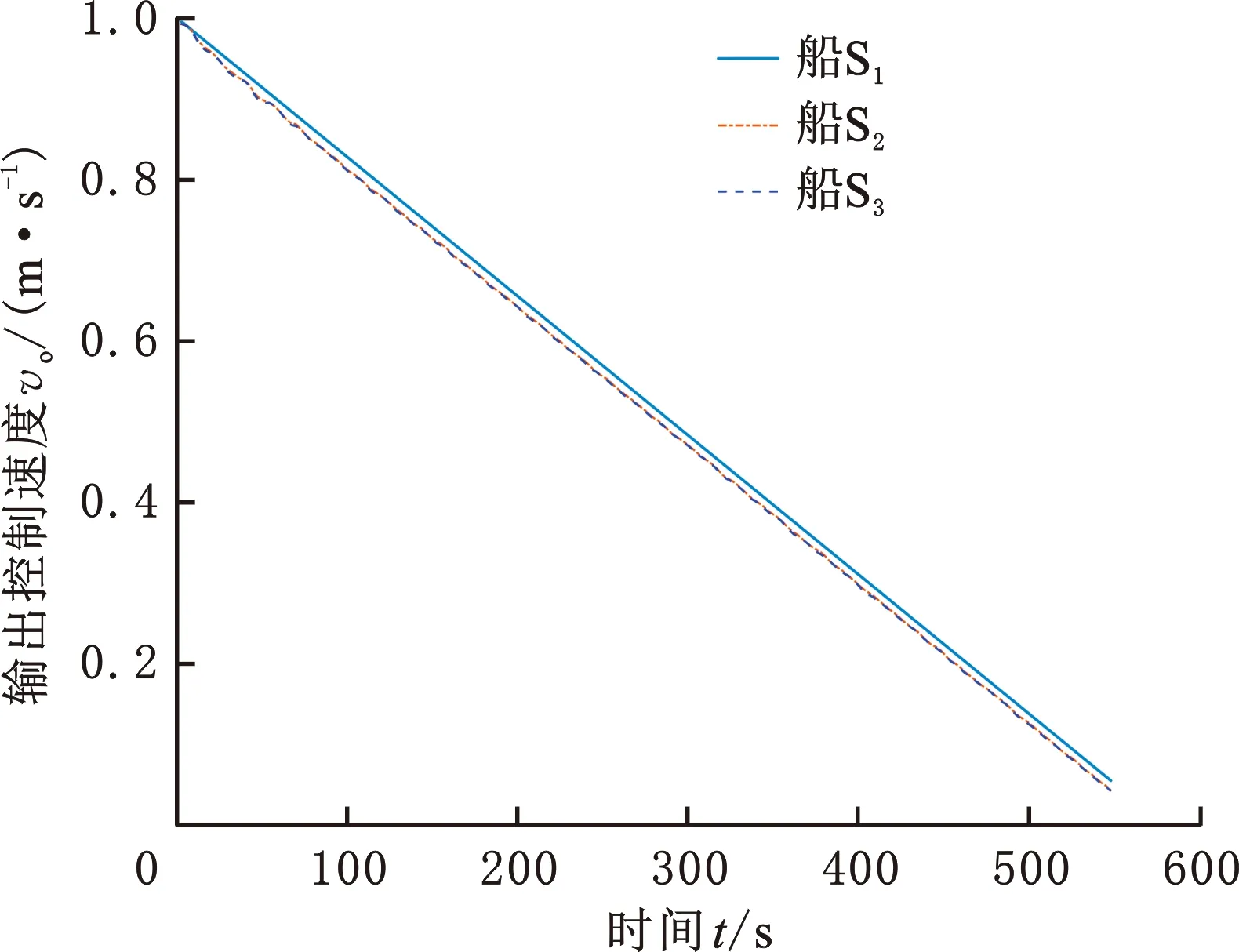
圖17 上層控制器輸出參考速度(速度-時(shí)間法)Fig.17 Upper controller output reference speed(speed-time method)

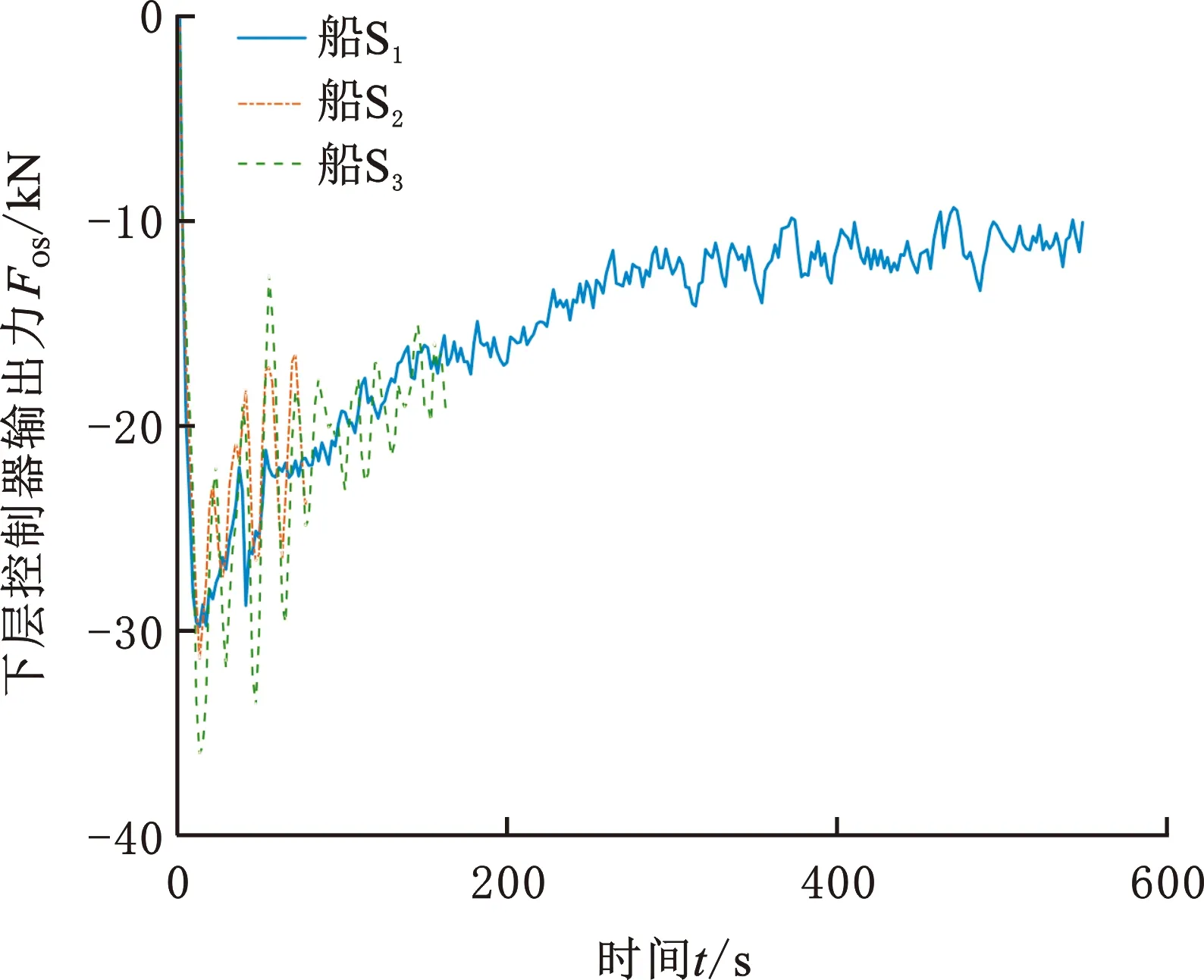
圖18 下層控制器輸出控制力(速度-時(shí)間法)Fig.18 Lower controller output force(speed-time method)

由圖15可以看出，在列隊(duì)停船過(guò)程中，船間距基本維持在設(shè)計(jì)跟船距離5 m附近，船間距1位于[4.9813，4.9992] m區(qū)間，船間距2位于[4.9934，5.0016] m區(qū)間。由圖16可以看出，在仿真進(jìn)行10 s內(nèi)，領(lǐng)航船保持速度航行，跟隨船航速?lài)@在領(lǐng)航船航速附近小范圍波動(dòng)，由于將領(lǐng)航船的參考速度與真實(shí)速度按一定權(quán)重混合后輸入上層控制器，故跟隨船避免了部分多余的航行操縱。由圖17可以看出，上層控制器能夠有效地根據(jù)領(lǐng)航船的航速變化對(duì)跟隨船的航速進(jìn)行控制，其輸出曲線基本與領(lǐng)航船參考速度曲線相同，其間保持的固定差距是龍格庫(kù)塔法和歐拉法解算的差距造成的。由圖18可以看出，下層控制器能夠有效應(yīng)對(duì)隨機(jī)干擾對(duì)船舶的影響，但同時(shí)對(duì)比三艘船的曲線后發(fā)現(xiàn)，由于跟隨船的裝載量大，動(dòng)力機(jī)構(gòu)性能較弱，控制器在進(jìn)行減速控制時(shí)會(huì)表現(xiàn)得比較激進(jìn)。

領(lǐng)航船按照速度-位移法完成停船得到的仿真結(jié)果如圖19～圖22所示。

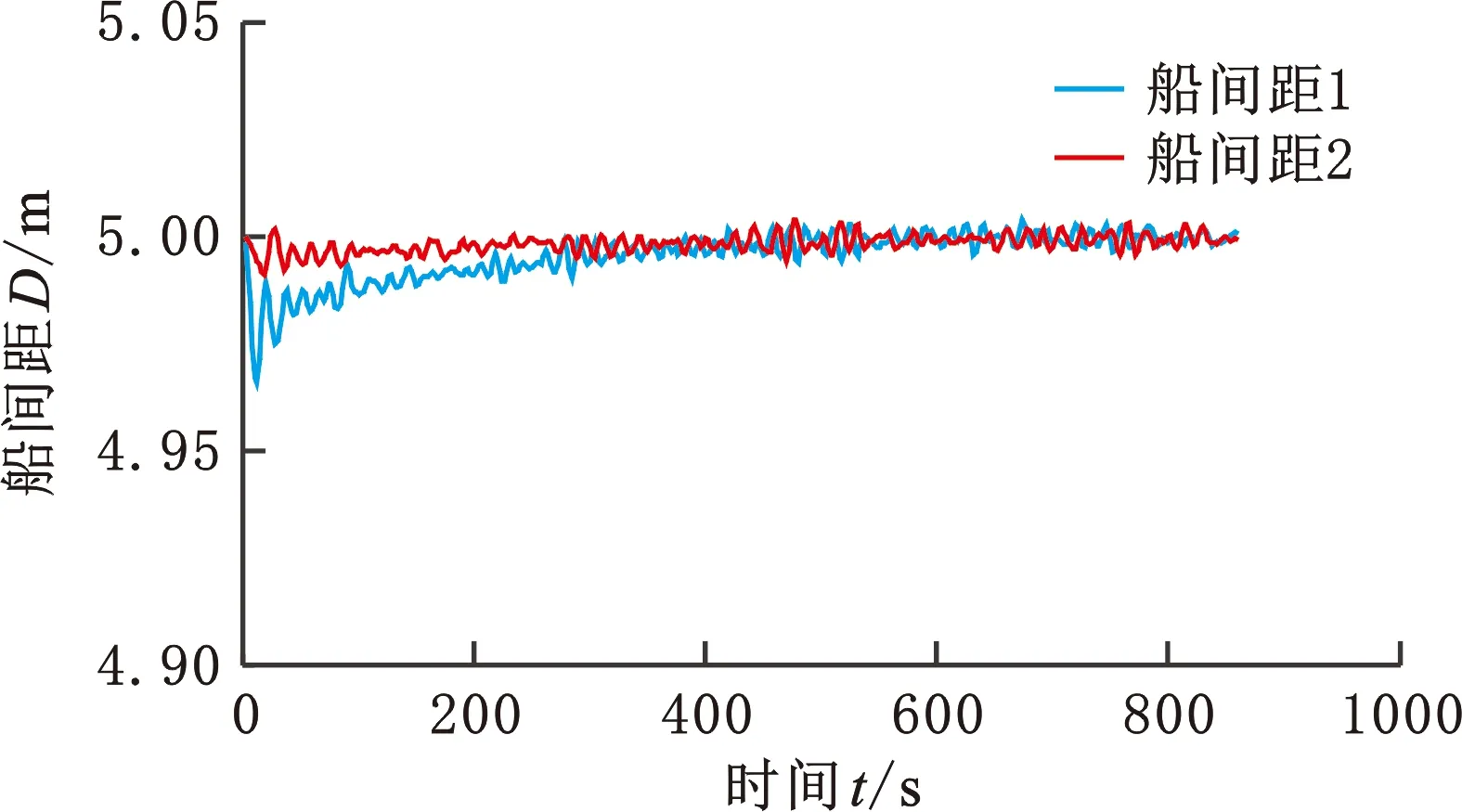
圖19 船間距動(dòng)態(tài)變化(速度-位移法)Fig.19 Dynamic change of ship spacing(speed-displacement method)

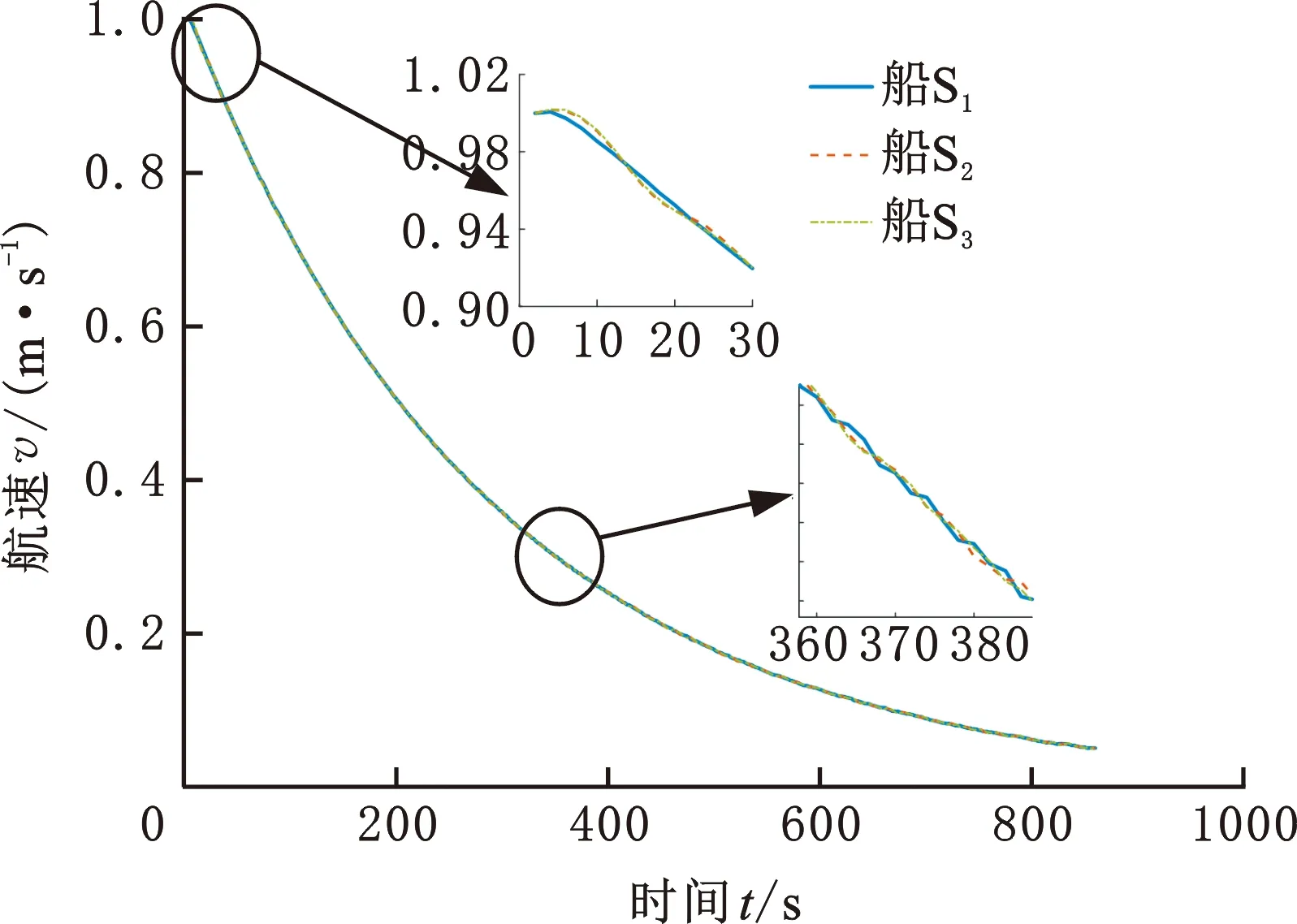
圖20 航速動(dòng)態(tài)變化(速度-位移法)Fig.20 Dynamic change of speed(speed-displacement method)

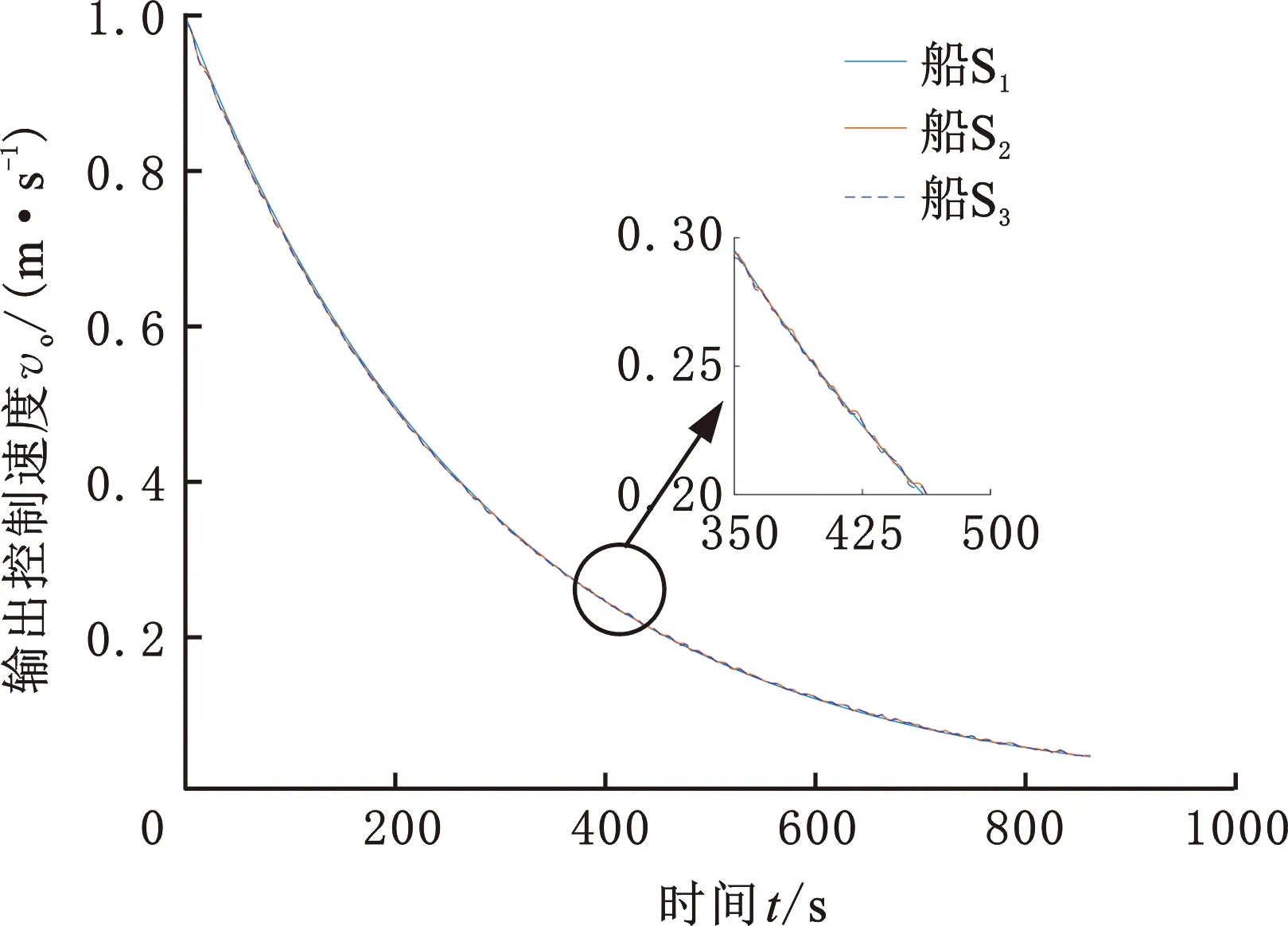
圖21 上層控制器輸出參考速度(速度-位移法)Fig.21 Upper controller output reference speed(speed-displacement method)

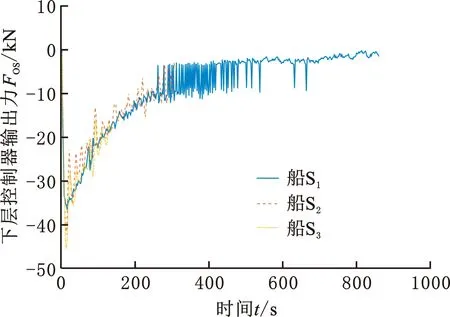
圖22 下層控制器輸出力(速度-位移法)Fig.22 Lower controller output force(speed-displacement method)

由圖19可以看出，按照速度-位移法完成停船的過(guò)程中，船間距同樣能夠維持在設(shè)計(jì)跟船距離5 m附近，船間距1位于[4.9622，5.0038] m區(qū)間，船間距2位于[4.9911，5.0040] m區(qū)間。由圖21和圖22可以看出，上、下層控制器的輸出量相比速度-時(shí)間法都有更明顯的波動(dòng)量，且跟隨船的下層控制器同樣表現(xiàn)更為激進(jìn)。利用4.2節(jié)的指標(biāo)對(duì)仿真結(jié)果進(jìn)行評(píng)價(jià)，結(jié)果見(jiàn)表2。

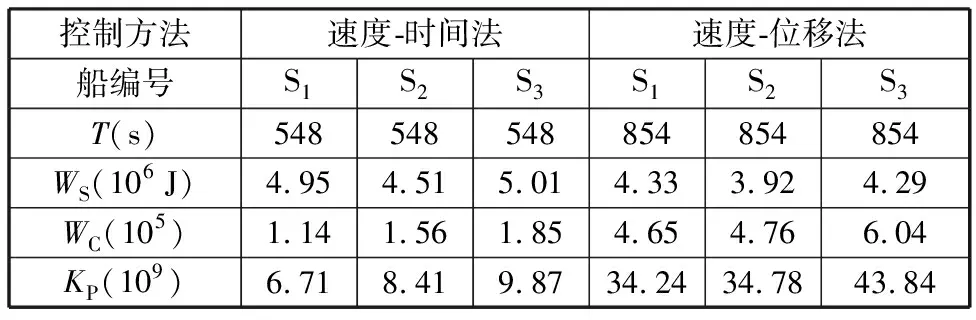
表2 船舶列隊(duì)運(yùn)動(dòng)評(píng)價(jià)指標(biāo)Tab.2 Evaluation index of ship platoon movement

由表2可以看出，采用相同的控制方法時(shí)，跟隨船的平順性有一定的犧牲；同時(shí)載重更大、動(dòng)力機(jī)構(gòu)性能更差的船舶在能耗方面表現(xiàn)更差。對(duì)比兩種控制方法，速度-時(shí)間法在平順性上表現(xiàn)更好，速度-位移法在經(jīng)濟(jì)性上表現(xiàn)更好。

5 結(jié)語(yǔ)

本文以船閘內(nèi)船舶運(yùn)動(dòng)仿真為基礎(chǔ)，借助船舶運(yùn)動(dòng)學(xué)和船舶動(dòng)力學(xué)模型，設(shè)計(jì)了基于模型預(yù)測(cè)控制的船舶入閘停船控制器，分兩種航速控制方法對(duì)控制效果進(jìn)行了驗(yàn)證，并設(shè)計(jì)了評(píng)價(jià)指標(biāo)對(duì)合理停船動(dòng)作進(jìn)行了討論。在單船完成閘室停船控制的基礎(chǔ)上，建立了狹窄水域中的直航船間距模型，設(shè)計(jì)了基于模型預(yù)測(cè)控制的船舶協(xié)同入閘航行集中控制器，并驗(yàn)證了其控制效果。該控制器可為船舶協(xié)同入閘航行安全間距保持及效率提升提供參考，為狹小水域列隊(duì)集中控制器的設(shè)計(jì)提供重要依據(jù)。

本文研究為單排列隊(duì)直線入閘航行場(chǎng)景，在后續(xù)研究中可加入兩排并行入閘場(chǎng)景，并行入閘在引航道中設(shè)計(jì)船舶旋回操縱性的異質(zhì)，容易出現(xiàn)安全隱患。另外，本文研究忽略了船閘水域中由于船-船距離、船-岸距離近帶來(lái)的船間效應(yīng)及岸壁效應(yīng)的影響，這在船舶低速航行入閘時(shí)會(huì)影響控制精度。后續(xù)研究可考慮三自由度運(yùn)動(dòng)中增加船閘水域中特殊環(huán)境的影響。