TLS密碼套件的流量數(shù)據(jù)隨機性分析

郭帥，程光，3，*

（1.東南大學 網(wǎng)絡空間安全學院，南京 211189； 2.計算機網(wǎng)絡和信息集成教育部重點實驗室（東南大學），南京 211189；3.網(wǎng)絡通信與安全紫金山實驗室，南京 211111）

加密流量的檢測與識別是網(wǎng)絡測量領域重要而又富有挑戰(zhàn)性的研究方向。加密流量在現(xiàn)有互聯(lián)網(wǎng)總體流量中的占比大幅增加，其中充斥著大量惡意程序流量與網(wǎng)絡攻擊流量，為網(wǎng)絡監(jiān)管與網(wǎng)絡空間治理帶來困難。由于密碼算法將網(wǎng)絡流量的原始信息掩蓋，基于明文內(nèi)容特征的識別方法在面對這些加密流量時難以奏效，加密流量的識別具有了較緊迫的需求與現(xiàn)實意義。加密流量識別在一般意義上指對經(jīng)過密碼算法加密后的數(shù)據(jù)在網(wǎng)絡傳輸中產(chǎn)生的字節(jié)序列進行檢測與識別，而被識別的對象則包括加密流量的內(nèi)容、應用程序、密碼算法等。根據(jù)加密流量的具體類型與應用場景的不同，又有針對VPN、安全傳輸層協(xié)議（transport layer security，TLS）及自定義或未知加密流量的識別。TLS協(xié)議作為現(xiàn)代Web網(wǎng)絡的主流加密通信協(xié)議，被大規(guī)模使用，針對TLS流量的識別研究在加密流量識別領域具有重要地位，本文通過TLS不同加密套件的流量數(shù)據(jù)隨機性分析，對TLS加密流量的密碼算法識別進行了研究。TLS密碼算法識別本質(zhì)上屬于密碼體制識別，指在未知明文、具體密碼算法與加密密鑰的情況下對密碼算法的體制與類型進行識別，是一種被動的唯密文攻擊手段。密碼體制與算法識別為加密流量的深層次分析提供了另一個角度與方向。

目前，網(wǎng)絡流量的密碼體制與算法識別主要有數(shù)學統(tǒng)計模型與機器學習2類，均以不同密碼體制或算法產(chǎn)生的密文在字節(jié)分布特征上具有可分的差異性為前提，通過提取密文的字節(jié)分布特征輸入預先建立的統(tǒng)計學模型或神經(jīng)網(wǎng)絡進行識別。密文字節(jié)分布的隨機性是衡量密碼體制與算法性能的重要指標，同樣也是對其進行識別的重要特征。2015年，吳楊等［1］設計了一種基于碼元頻數(shù)檢測、塊內(nèi)頻數(shù)檢測及游程檢測的算法對AES、Camellia、DES、3DES及SMS4密文的隨機性度量值取值個數(shù)進行了統(tǒng)計分析。2016年，丁偉和談程［2］介紹了一種基于密文分析的密碼識別方法，該方法使用支持向量機（SVM）對密碼體制進行識別。2018年，黃良韜等［3］提出了一種基于隨機森林的分層密碼體制識別定義系統(tǒng)，相比單層識別方案有約20%的提升。2018年，李洪超［4］提出了一種基于SVM、隨機森林和決策樹的集成學習方法，通過了15種隨機性測度對電子密碼本（ECB）和密文分組鏈接（CBC）二種加密模式的識別。2019年，趙志誠等［5］提出了一種基于隨機森林的密碼體制識別方法，以美國國家標準與技術研究院（NIST）的隨機性測試套件為基礎，構(gòu)建了54種密文特征，以顯著高于隨機識別的準確率完成對AES、DES、3DES、IDEA、Blowfish及Camellia六種密碼體制的兩兩區(qū)分問題。2021年，王旭等［6］結(jié)合Relief特征選擇算法和異質(zhì)集成學習，提出了一種可適應多種密碼體制識別情景的動態(tài)特征識別方案，比較了3類不同密碼體制識別情景。

以上工作均以密文字節(jié)序列的分布隨機性作為基礎構(gòu)建差異特征模型，但大多僅對DES、3DES等老舊密碼算法與ECB、CBC等簡單加密工作模式進行分類，對于TLS協(xié)議中常用的AES、ChaCha20密碼算法及GCM加密模式均沒有進行研究與分析，因此，上述工作在加密流量的密碼算法識別上作用有限。本文將從實際現(xiàn)網(wǎng)加密流量中的密碼算法使用比例出發(fā)，分析主流密碼算法與其他傳統(tǒng)密碼算法在密文隨機性分布上的特征，并嘗試使用2種機器學習方法對AES、RC4與ChaCha20在不同工作模式下的密文進行分類識別，以探究加密流量中密碼套件的選擇與密碼算法在純密文、有無特征情況下的可識別性問題。

1 TLS密碼套件分析

TLS密碼套件是指在TLS連接握手、加密通信與數(shù)據(jù)完整性檢驗等過程中被使用的算法集合，包含密鑰交換算法、對稱密碼算法和消息摘要算法等元素［7］。

1.1 TLS密碼套件組成

根據(jù)TLS版本的不同，其密碼套件組成也不同，一個典型的TLS1.2版本密碼套件格式如圖1（a）所示，一個典型的TLS1.3版本密碼套件組成如圖1（b）所示。

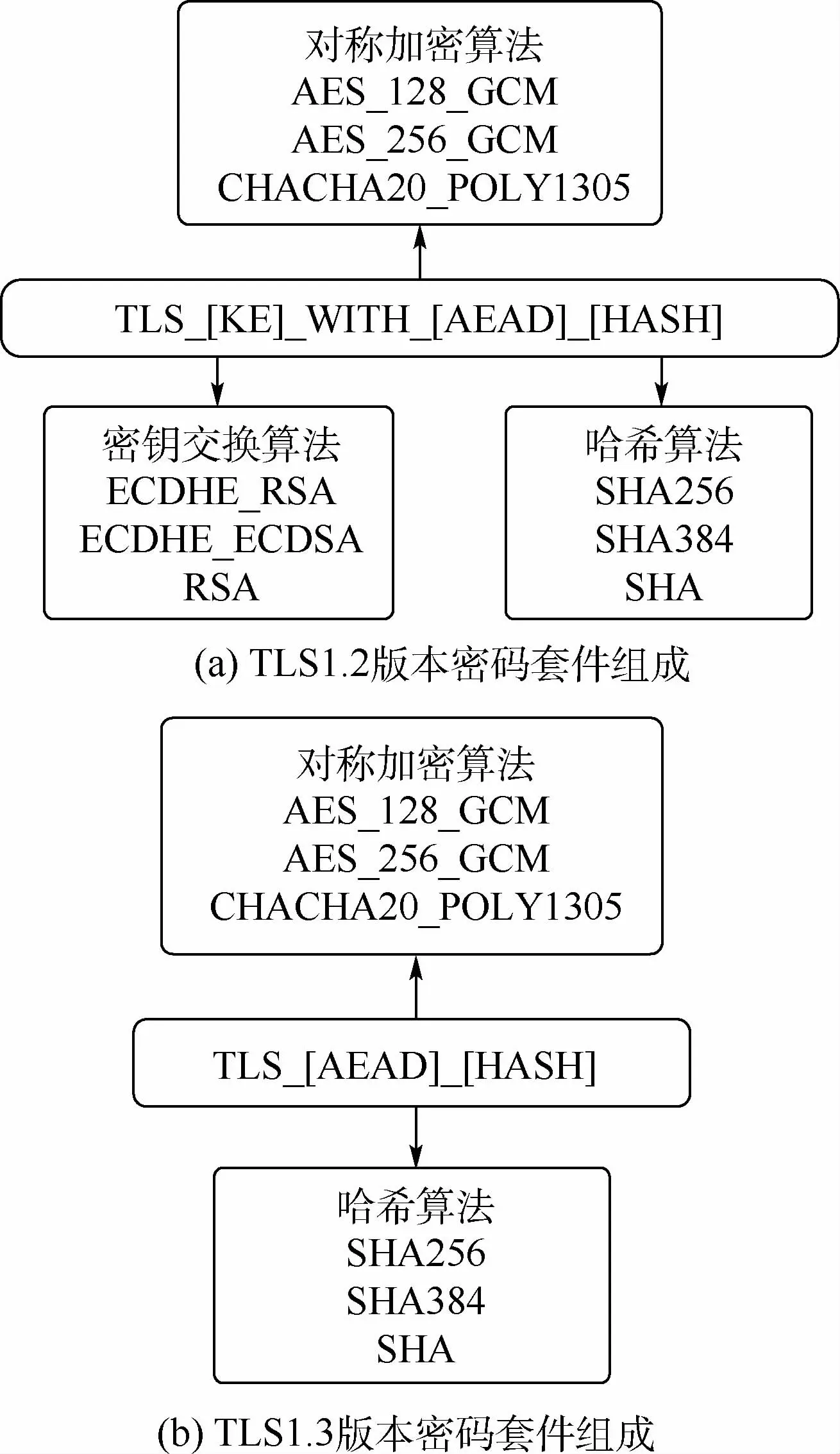
圖1 TLS密碼套件組成Fig.1 Composition of TLS cipher suite

需要說明的是，包含“WITH”字段的均為TLS1.2及以下版本支持的密碼套件，TLS1.3版本默認使用ECDHE作為密鑰交換算法，因此密碼套件不需要表明，TLS1.3版本支持的密碼套件編號為4 865～4 869。雖然TLS1.2版本與TLS1.3版本加密套件都使用相同的編號格式，但是二者并不通用。經(jīng)過實際調(diào)研，TLS1.3版本的加密套件只可能是編號為4 865、4 866、4 867的3種情況。

1.2 現(xiàn)網(wǎng)流量中的各加密套件占比

本文中使用的現(xiàn)網(wǎng)流量采集自CERNET華東北網(wǎng)絡中心邊界路由，采集周期為7 d，抽取每天固定時間段內(nèi)的流量作為樣本，經(jīng)解析得到TLS流1 415 375條，可提取出加密套件的流共613 922條，占比排名前20的密碼套件如表1所示。

表1 現(xiàn)網(wǎng)流量中各TLS密碼套件比例Table 1 Proportion of TLS cipher suites in actual network traffic

分析結(jié)果顯示，大部分TLS流采用的密碼套件是TLS＿ECDHE＿RSA＿WITH＿AES＿128＿GCM＿SHA256，占比為59.39%；排名前5的密碼套件占總體的88.54%，其中前4名均為AES的GCM模式；在占比前20名的密碼算法中，除了1個RC4與2個ChaCha20算法外，均為AES密碼算法；這20個加密套件占總體樣本的99.73%。除此以外，在這批樣本中還觀測到了少量的TLS1.3版本專用加密套件，說明樣本中包含少量TLS1.3流量（少于0.02%）。

上述結(jié)果證明，在真實網(wǎng)絡的TLS加密流量中，使用AES作為對稱密碼算法的情況占絕大部分（97.03%），其余的算法為ChaCha20與RC4。另外，在所有加密套件中均沒有發(fā)現(xiàn)使用ECB模式的密碼算法。

2 密碼算法的密文隨機性檢測

密文隨機性指經(jīng)密碼算法加密產(chǎn)生的數(shù)據(jù)在字節(jié)分布上的隨機程度，密文隨機性檢測即指對密文字節(jié)分布的隨機程度進行度量。本文使用了2種方法對密文的隨機性進行檢測：①密文圖像重構(gòu)法是一種主觀的隨機性檢測方法，從宏觀角度觀察密文的字節(jié)分布特征；②基于SP800-22測試套件的檢測方法則從客觀和微觀的角度對密文的隨機性進行刻畫。

2.1 基于密文圖像重構(gòu)法的隨機性檢測

本節(jié)將使用密文圖像重構(gòu)后的可辨別性作為標準對表2中所示的密碼算法與工作模式進行密文隨機性的檢測。基于密文圖像重構(gòu)的隨機性檢測機制是直觀且主觀的。由于對稱密碼算法在加密后不會改變原始數(shù)據(jù)的長度，將圖像數(shù)據(jù)加密后再按照原始尺寸與分辨率重新排列密文比特序列，可將密文重構(gòu)成與原始數(shù)據(jù)相同大小的圖像。

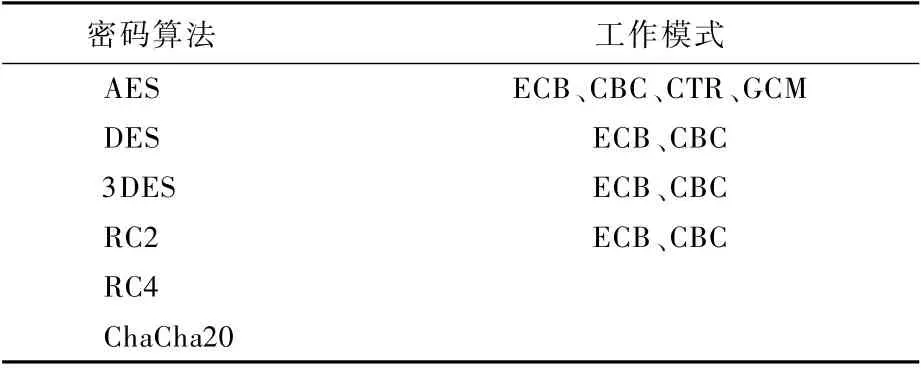
表2 參與實驗的密碼算法與工作模式Table 2 Cipher algor ithms and wor king modes involved in experiment

通過觀察密文圖像與原始圖像，可以直觀地感受到不同密碼算法與工作模式對數(shù)據(jù)的影響，也可以觀察到不同密碼算法在不同的工作模式下，其密文隨機性在宏觀上的表現(xiàn)。

2.1.1 實驗方法

本節(jié)實驗采用如圖2所示的卡通猴圖像作為樣本，該圖像為二值圖（只包含黑色和白色2種顏色），本質(zhì)上是由0（白色）和1（黑色）組成的比特序列，圖像大小為4 096×4 096，共16 777 216 bit（2 MByte）。圖像的比特序列將作為密碼算法的輸入。

圖2 用于實驗的圖像Fig.2 Images for experiments

由于表2中各密碼算法及工作模式的分塊大小均為2的整倍數(shù)，輸入樣本的數(shù)據(jù)量可被完整分塊無需填充，加密后的數(shù)據(jù)量和尺寸不變。將密文的比特序列重新按照4 096×4 096的分辨率進行排列，可將密文組成一幅與原始圖像大小相同的圖像。通過肉眼觀察、對比密文圖像與原始圖像在內(nèi)容特征上的相似性，可以得到密文在字節(jié)分布上的宏觀特征。

2.1.2 實驗結(jié)果與分析

實驗結(jié)果如圖3所示。

圖3 密文圖像實驗結(jié)果Fig.3 Experimental results of ciphertext image

通過實驗結(jié)果可以看到，對于所有可選分組模式的密碼算法，在ECB模式下均可觀察到原始圖像的大致輪廓，而其他模式或密碼算法的結(jié)果在宏觀上均為分布均勻的黑白像素，沒有肉眼可以觀察到的顯著特征。通過分析，本文認為這一現(xiàn)象是由ECB本身的工作原理造成的，在ECB模式下，明文塊加密后按順序直接拼接。因此，當圖像分辨率足夠高時（明文長度足夠長），明文分塊過小（128 bit或256 bit）導致僅塊內(nèi)加密并不會影響整體的結(jié)構(gòu)，而其他工作模式或密碼算法對并不是分塊加密后的明文進行線性地簡單排列，破壞了整體結(jié)構(gòu)，使密文無法顯現(xiàn)出原始數(shù)據(jù)具有的輪廓特征。

為了驗證密文圖像不存在肉眼難以辨認的微小規(guī)律性特征，本節(jié)將原始圖像、AES＿ECB、AES＿CBC、AES＿GCM與ChaCha20密文圖像的二維離散傅里葉頻率圖［8］作為補充實驗，結(jié)果如圖4所示。

圖4 密文圖像的傅里葉頻率圖Fig.4 Fourier frequency diagram of ciphertext image

通過觀察實驗結(jié)果可發(fā)現(xiàn)，原始圖像和ECB模式下的圖像在經(jīng)過傅里葉變換后，仍舊保留了大量可分辨的高頻和低頻特征，能量分布并不均勻，證明其密文圖像具有較顯著的規(guī)則結(jié)構(gòu)；其他加密模式的傅里葉變換功率圖已無明顯的特征，高低頻分布均勻，能量分布均勻，證明密文圖像無顯著的規(guī)則結(jié)構(gòu)。

根據(jù)上述結(jié)果，本文認為參與實驗的密碼算法在ECB工作模式下，其密文的隨機性分布較差，具有顯著的、肉眼可觀測的特征。由于ECB工作模式加密時的線性特點，當原始數(shù)據(jù)的數(shù)據(jù)量足夠大時，使用ECB工作模式進行加密，密文數(shù)據(jù)將會一定程度保留原始數(shù)據(jù)的結(jié)構(gòu)特征，為密文攻擊留下隱患。

2.2 基于SP800-22測試套件的隨機性檢測

工業(yè)界具有較廣泛影響的隨機性測試與度量方法是NIST于2010年修訂的SP800-22 Rev1a標準［9］，該標準包含15個測度指標用于對密碼算法和偽隨機數(shù)生成算法產(chǎn)生數(shù)據(jù)的隨機性進行衡量。SP800-22 Revla標準包含的15個指標與測量方法如下：

1）monobit test。即整個二進制序列中0 bit和1 bit的比例，完全隨機序列中二者應具有相同或相近的頻次。

2）frequency within block test。本質(zhì)上還是monobit test，只不過該測度將待測數(shù)據(jù)分塊，再統(tǒng)計并在每塊內(nèi)執(zhí)行monobit test。

3）runs test。n個相同的二進制位被視為1個長度為n的游程。游程檢測通過統(tǒng)計一段密文中所包含的不同長度游程的數(shù)量，判斷其是否與理想隨機數(shù)據(jù)的游程數(shù)量一致。

4）longest run ones in a block test。分塊內(nèi)最長連續(xù)1 bit序列的長度。

5）binary matrix rank test。將數(shù)據(jù)的比特序列組成矩陣后，計算矩陣的秩。

6）dft test。將數(shù)據(jù)通過傅里葉變換轉(zhuǎn)換到頻域，檢測其頻率譜中能量尖峰的分布情況，目的是檢測待檢驗信號的周期性。

7）non overlapping template matching test。用來測試數(shù)據(jù)中是否出現(xiàn)了過多的非周期模式序列。對于n bit長度的模式序列，使用1個n bit長度的滑動窗口進行匹配，如果在當前位置匹配失敗，窗口向后滑動1 bit，如果當前位置匹配一致，窗口向后滑動n bit，繼續(xù)進行匹配。

8）overlapping template matching test。該指標與non overlapping template matching test相似，用來測試數(shù)據(jù)中是否出現(xiàn)了過多的非周期模式序列，不同之處在于該指標在匹配成功后只滑動1 bit。

9）linear complexity test。計算輸入數(shù)據(jù)的線性復雜度，評估其與完全隨機序列的差距。

10）serial test。該指標檢測所有連續(xù)m bit的序列在輸入數(shù)據(jù)中出現(xiàn)的頻次。

11）approximate entropy test。計算輸入數(shù)據(jù)的近似熵，評估其與完全隨機序列的差距。

12）cumulative sums test。檢測輸入數(shù)據(jù)中的部分比特和是否太大或太小。

13）random excursion test。檢測輸入數(shù)據(jù)中某一狀態(tài)出現(xiàn)的次數(shù)是否遠超完全隨機序列。

14）random excursion variant test。檢測輸入數(shù)據(jù)中某一狀態(tài)在1次隨機游程中出現(xiàn)的次數(shù)是否遠超完全隨機序列。

15）maulers universal test。檢測輸入數(shù)據(jù)是否可以被壓縮算法顯著壓縮。

SP800-22 Revla標準采用顯著性檢驗模型對輸入數(shù)據(jù)的隨機性進行度量，即檢驗輸入數(shù)據(jù)與假設的完美隨機序列之間的統(tǒng)計學差距。由于假設檢驗不屬于本文主要內(nèi)容，在此不再贅述。當某一指標的指數(shù)大于0.01時，有99%的置信度認為輸入數(shù)據(jù)在該指標上符合完全隨機性，指數(shù)越接近1，說明輸入數(shù)據(jù)在該指標上越接近完全隨機序列。

基于SP800-22 Revla測試套件的隨機性檢測將圖2的原始數(shù)據(jù)經(jīng)過AES＿GCM、AES＿ECB、RC4和ChaCha20密碼算法加密后，輸入SP800-22 Revla隨機性測試套件，對密文的15個隨機性指標進行檢測，其結(jié)果如表3所示。通過實驗結(jié)果可知，AES＿GCM、RC4及ChaCha20這3種主流TLS密碼算法在隨機性上表現(xiàn)優(yōu)秀，通過了SP800-22 Revla測試套件的全部指標，而AES＿ECB模式僅通過了3項，其余指標均未通過，與原始數(shù)據(jù)幾乎相同。因此，ECB模式無法完全掩蓋原始數(shù)據(jù)具有的非隨機特征，與其他密碼算法相比在密文的隨機性上表現(xiàn)較差，具有可區(qū)分性，容易遭受密碼分析攻擊。

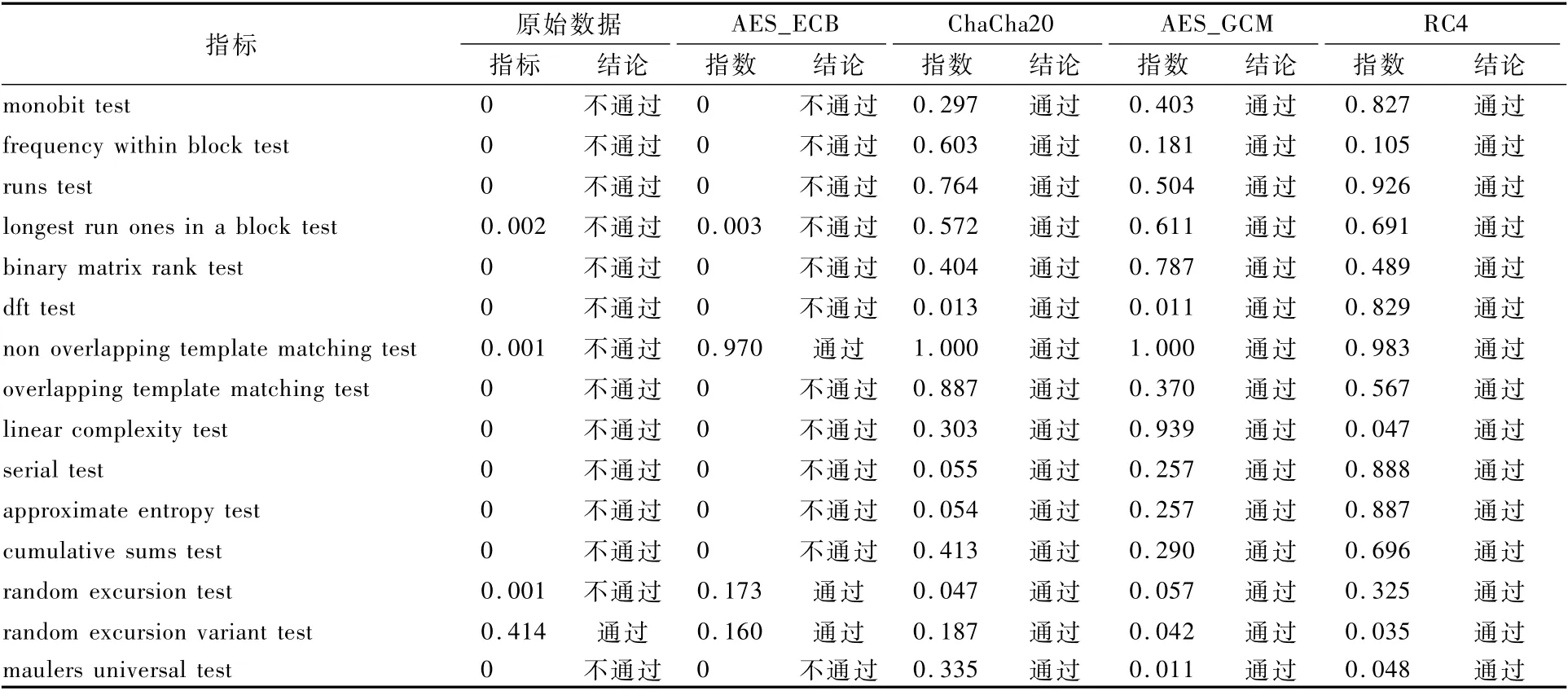
表3 圖2在SP800-22測試套件上的隨機性測度檢測結(jié)果Table 3 SP800-22 randomness measurement test results of Fig.2

3 密碼算法類型識別的可行性分析

應用于密碼算法識別與加密流量分類的主要機器學習方法有2類：一類是以SVM［10］、決策樹［11］、隨機森林［12］等為代表的傳統(tǒng)機器學習方法；另一類是以多層感知機（MLP）［13］、卷積神經(jīng)網(wǎng)絡（CNN）［14］、循環(huán)神經(jīng)網(wǎng)絡（RNN）［15］等模型為代表的深度學習方法。使用傳統(tǒng)的機器學習方法需要通過特征工程提取原始數(shù)據(jù)的相關特征作為訓練數(shù)據(jù)，而使用深度學習方法可以直接輸入原始數(shù)據(jù)，依托深度學習模型的自主特征挖掘能力進行訓練。本文將分別使用CNN和隨機森林這2種在相關問題中被證明有效的模型，進行基于特征和原始數(shù)據(jù)的無特征密碼算法類型與工作模式的識別可行性分析。

3.1 識別方案

3.1.1 基于CNN的無特征識別

CNN是包含卷積計算且具有深度結(jié)構(gòu)的前饋神經(jīng)網(wǎng)絡，在計算機視覺、圖像分析和處理等領域發(fā)揮了巨大作用，其接收1個多通道矩陣作為輸入，經(jīng)過卷積層、池化層、全連接層等網(wǎng)絡結(jié)構(gòu)，最后輸出1個向量作為分類結(jié)果。LeNet5［14］是最經(jīng)典的CNN網(wǎng)絡模型，最早被應用于手寫數(shù)字的識別，是一個十分類問題，其輸出層尺寸為10×1。為適應實驗需求，本文對其輸出層結(jié)構(gòu)進行了修改，具體結(jié)構(gòu)組成依次為輸入層（32×32，1通道）、二維卷積層（28×28，6通道）、最大池化層（14×14，6通道）、二維卷積層（10×10，16通道）、最大池化層（5×5，6通道）、全連接層（120×1，單通道）、全連接層（84×1，單通道）及輸出層（5×1，單通道），詳細結(jié)構(gòu)如圖5所示。

圖5 用于密碼算法識別的CNN結(jié)構(gòu)Fig.5 CNN structure for cipher algorithm recognition

該模型對應一個五分類問題，即對AES＿ECB、AES＿CBC、AES＿GCM、RC4、ChaCha20五種不同的密碼算法與模式進行識別。模型的輸入為原始流量數(shù)據(jù)經(jīng)過處理后生成的尺寸為32×32的字節(jié)矩陣，輸出為1×5的向量，代表最終的密碼算法類型分類結(jié)果。整個訓練過程共進行200次迭代。

3.1.2 基于隨機森林的有特征識別

隨機森林是一種集成學習分類方法［16］，通過建立多個獨立模型的組合來解決一個分類問題，其會生成多個分類器，每個分類器各自學習和做出決策，這些決策最后會通過投票形成一個單一的分類結(jié)果，因此在一般情況下，集成學習的結(jié)果將優(yōu)于一個單獨分類器。隨機森林使用多個獨立決策樹的決策來確定最后的分類結(jié)果，因此，其也是一種集成學習方法。

本文將使用決策樹作為分類模型，進行不同密碼算法與工作模式的識別。隨機森林是基于特征的分類器模型，不能直接輸入原始數(shù)據(jù)，需要進行特征的提取。本文將使用SP800-22 Revla的全部測度作為樣本的特征，組成一維特征向量F：

式中：xi代表SP800-22 Revla測試套件中的1個測度值；n為特征向量長度，本文中n＝15。

使用樣本特征向量組成各密碼算法的樣本數(shù)據(jù)集Salgo，樣本數(shù)據(jù)集包含了該密碼算法或工作模式用于訓練和測試的所有樣本：

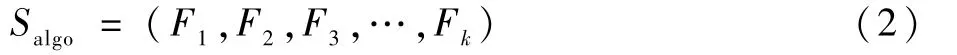
式中：algo指某一種密碼算法或工作模式；Fj為第j個樣本的特征向量；k為樣本數(shù)量，在本文中k＝5 000，即每一類密碼算法或工作模式有5 000個樣本。

為了完成隨機森林的二分類任務，需要從各密碼算法或工作模式數(shù)據(jù)集中抽取2個組成用于模型訓練和測試的擴展數(shù)據(jù)集T與標簽集L：式中：Am代表擴展數(shù)據(jù)集T中第m個樣本的密碼算法或工作模式類型，取值為1或2，代表二分類問題中的第1類或第2類。

基于隨機森林的有特征識別采用了十折交叉驗證方法，因此，只需要對擴展數(shù)據(jù)集T進行隨機打亂排序，而不需要手動進行訓練集和測試集的劃分。在進行模型的訓練時，輸入打亂順序后的擴展數(shù)據(jù)集T，模型輸出預測標簽集Lpre，將Lpre與原始標簽集L對比可得到模型的分類準確率。

3.2 實驗方法

3.2.1 數(shù)據(jù)采集方法

本節(jié)實驗采用TLS1.2加密網(wǎng)絡流量作為基礎數(shù)據(jù)樣本，根據(jù)第1節(jié)對現(xiàn)網(wǎng)流量中密碼套件的占比分析，實驗采用如表4所示的4種密碼套件產(chǎn)生流量。此外，為了驗證模型的有效性，除了表4中列出的4種密碼套件，本文還加入了AES＿ECB模式，即總共5種密碼算法。

表4 實驗采用的密碼套件Table 4 Cipher suite used in experiment

需要說明的是，在TLS密碼套件中并不存在使用ECB的選項，因此，無法通過模擬產(chǎn)生TLS流量來獲取AES＿ECB加密的流量。本文將使用OpenSSL中的AES＿ECB加密模塊對原始數(shù)據(jù)進行加密，直接獲得ECB工作模式下的樣本。這種方法在本質(zhì)上與TLS產(chǎn)生加密數(shù)據(jù)的過程類似，可以避免因樣本產(chǎn)生方法不同而對實驗結(jié)果產(chǎn)生影響。

4種密碼套件的主要密碼算法分別是AES＿CBC、AES＿GCM、ChaCha20及RC4，使用比例在本文采集的現(xiàn)網(wǎng)流量中達到90%。因此，這4種密碼算法具有足夠的代表性，如果能夠?qū)ζ溥M行區(qū)分，具有較大的現(xiàn)實意義。TLS流量由本地模擬環(huán)境產(chǎn)生，原始內(nèi)容為HTTP形式的響應數(shù)據(jù)，其身體部分為長度1 000～1 200 Byte的郵件文本序列［17］，加上約160 Byte的HTTP頭部，整個負載加密后長度在1 300～1 500 Byte以內(nèi)。通過反向代理，將HTTP流量封裝成TLS流量，本節(jié)實驗僅使用1 024 Byte長度的加密數(shù)據(jù)，因此，1個樣本僅需1次HTTP請求即可。AES＿ECB使用同樣的原始數(shù)據(jù)，直接通過OpenSSL的加密模塊生成1 024 Byte長度的加密數(shù)據(jù)。

本節(jié)實驗一共使用20 000個密文樣本，5種密碼算法或工作模式的樣本數(shù)量相同（每種5 000個樣本）。在基于CNN的無特征識別中，從整個數(shù)據(jù)集中隨機抽取80%作為訓練樣本，20%作為測試樣本；在基于隨機森林的有特征識別中，從整個數(shù)據(jù)集中提取2種密碼算法或工作模式的樣本構(gòu)成擴展數(shù)據(jù)集，由于使用十折交叉驗證，無需手動劃分訓練集和測試集。

3.2.2 數(shù)據(jù)預處理方法

按照圖6所示的方法，對TLS樣本流量的應用負載部分進行提取。首先，根據(jù)各密碼算法的加密規(guī)則去除其頭部和尾部的初始化向量、MAC校驗碼等附加部分，剝離出純密文部分。然后，將純密文部分裁剪為1 024 Byte長度（由于流量生成時長度最低為1 300 Byte，不存在密文長度不夠時的填充問題，避免干擾），AES＿ECB的密文無需處理，可直接生成1 024 Byte長度的樣本。

圖6 樣本預處理方法Fig.6 Sample pretreatment method

在基于CNN的無特征識別中，將1 024 Byte的樣本數(shù)據(jù)按順序排列成一副尺寸為32像素×32像素的256色階的單通道灰度圖（即每個像素為1 Byte大小，代表0～255的不同黑白色階，32×32＝1 024）。按照分組密碼算法16 Byte的分組長度，該圖片的1行包含2個密文分組，每張圖包含64個密文分組，且原始密文數(shù)據(jù)的順序按從左到右、從上到下進行排列。

圖7為一個經(jīng)過圖像化處理的樣本，包含1 024 Byte的純密文。

圖7 經(jīng)處理后的樣本Fig.7 Processed samples

在基于隨機森林的有特征識別中，將1 024 Byte長度的樣本數(shù)據(jù)輸入SP800-22 Revla測試套件，獲取每一個樣本的15個隨機測度，并按照式（1）～式（4）生成對應的擴展數(shù)據(jù)集T和標簽集L，作為隨機森林分類器的輸入。

3.3 實驗結(jié)果

3.3.1 CNN模型識別結(jié)果

圖8為訓練過程中訓練集準確率和測試集準確率的變化。可以看到，隨著迭代次數(shù)的增加，訓練集準確率持續(xù)上升，在第125個迭代時逼近100%，但測試集準確率卻始終徘徊在約20%處，且整體呈現(xiàn)下降趨勢，這說明在訓練的早期模型可能就已經(jīng)出現(xiàn)了過擬合現(xiàn)象。出現(xiàn)過擬合現(xiàn)象的原因有很多，如模型過于簡單、樣本過少、訓練時間過長、樣本噪聲過大等。由于本節(jié)實驗訓練過程中，訓練集準確率持續(xù)上升，測試集準確率一直處于下降狀態(tài)，說明模型可以挖掘和學習到訓練集樣本的特征，但是無法將這種特征推廣到測試集或其他數(shù)據(jù)集，也說明通過深度學習模型從純密文樣本挖掘到的全局特征是“隨機”的，即對于各種密碼算法，其密文特征并沒有統(tǒng)一模式，這與密碼算法的本質(zhì)要求是一致的。

圖8 訓練過程中準確率的變化Fig.8 Change of accuracy during training

最終，該模型在AES＿ECB、AES＿CBC、AES＿GCM、ChaCha20、RC4這5種密碼算法識別問題上的準確率為20.92%，分類結(jié)果的混淆矩陣如圖9所示，該模型在此處的五分類問題上與隨機猜測的準確率一致。因此，本文認為LeNet5這一深度學習模型在本文的實驗環(huán)境下，無法解決AES＿ECB、AES＿GCM、AES＿CBC、ChaCha20及RC4純密文數(shù)據(jù)的五分類問題，即使是隨機性表現(xiàn)較差的AES＿ECB，也無法通過純密文負載與其他密碼算法進行區(qū)分。

圖9 分類結(jié)果混淆矩陣Fig.9 Confusion matrix of classification results

3.3.2 隨機森林模型識別結(jié)果

本文使用隨機森林進行密碼算法間的二分類問題，共有5種密碼算法需要分類，因此，可以形成10個不同的二分類問題，即隨機森林的輸入為10個擴展數(shù)據(jù)集T和標簽集L。隨機森林的二分類識別結(jié)果如表5所示。

通過表5中的結(jié)果可知，除AES＿ECB外，其余密碼算法或工作模式的二分類準確率均約為50%，與隨機猜測的準確率幾乎相同。而包含AES＿ECB的二分類準確率均高于50%，但均低于60%，識別效果略高于隨機猜測。

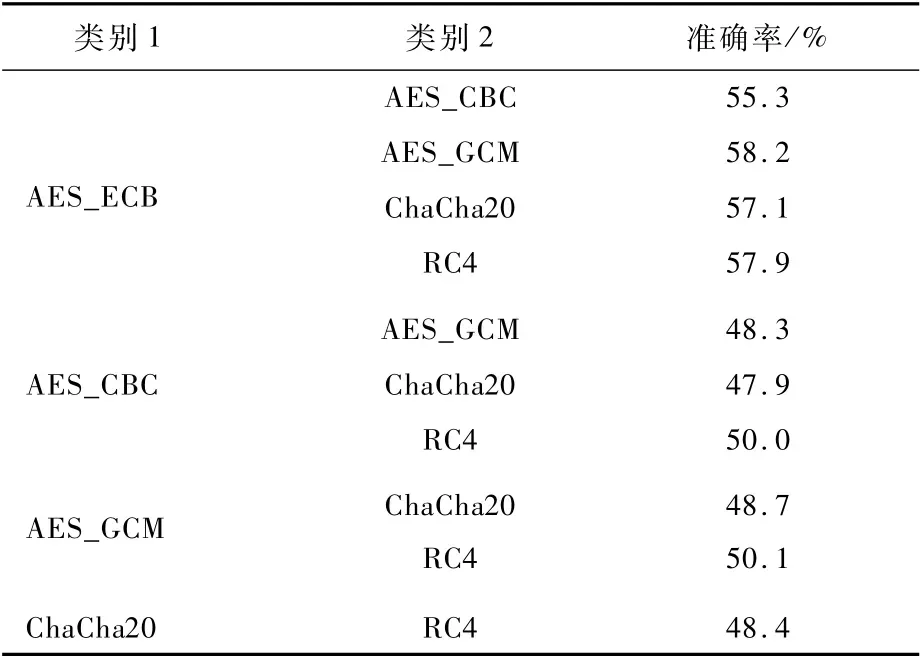
表5 隨機森林二分類準確率Table 5 Accuracy of random forest classification

值得注意的是，該結(jié)果所表現(xiàn)出的AES＿ECB與其他密碼算法的隨機性差異并沒有表3中顯著。本文認為這與原始數(shù)據(jù)本身的隨機性有關，表3中的結(jié)果由圖2經(jīng)各密碼算法加密后進行隨機性檢測得出，圖2的原始數(shù)據(jù)在絕大多數(shù)隨機性測度上都接近0。同時，AES＿ECB無法掩蓋原始數(shù)據(jù)的字節(jié)分布特征，導致經(jīng)AES＿ECB加密后的密文與其他密碼算法的密文存在巨大差異。在本節(jié)實驗中，原始數(shù)據(jù)來源于網(wǎng)絡郵件數(shù)據(jù)集，在網(wǎng)絡流量背景下比圖2更具有代表性，其本身的隨機性就比圖2強，因此，經(jīng)過AES＿ECB加密后與其他密碼算法的差異沒有表3中顯著。雖然對AES＿ECB與其他密碼算法的分類結(jié)果不顯著，但仍高于隨機猜測，證明本文模型在密碼算法的分類上具有一定有效性；而對于除AES＿ECB外的其他密碼算法或工作模式，在本文中的實驗環(huán)境下無法做到有效的區(qū)分。

4 結(jié) 論

本文通過對現(xiàn)網(wǎng)流量中TLS密碼套件使用情況，以及通過實驗對各類對稱密碼算法在不同工作模式下的密文隨機性及抵抗密碼體制識別能力上的表現(xiàn)進行比較，得出以下結(jié)論：

1）在現(xiàn)網(wǎng)流量中，AES是TLS協(xié)議中使用最廣泛的對稱密碼算法，占總體的97.03%；GCM是AES算法中最常使用的工作模式，占總體的90.98%。現(xiàn)有關于密碼算法識別的工作大多沒有涉及AES＿GCM 與ChaCha20這2種主流密碼算法，因此，并不適用于TLS網(wǎng)絡流量中的密碼算法別問題。

2）TLS中各類對稱密碼算法在ECB工作模式下均具有較差的密文隨機性，其密文帶有顯著的原始數(shù)據(jù)結(jié)構(gòu)特征。在非ECB模式下，密文隨機性表現(xiàn)良好，密文的傅里葉頻率圖能量分布均勻，其中AES＿GCM、AES＿CBC、ChaCha20及RC4密文均可通過SP800-22 Revla的全部指標。

3）AES＿ECB、AES＿CBC、AES＿GCM、ChaCha20及RC4這5種密碼算法或其分組模式均可在一定程度上抵御基于無特征識別的分析攻擊，但AES＿ECB模式無法抵御基于有特征識別的分析攻擊。

4）進行加密流量的分析時，應同時考慮數(shù)據(jù)的非加密與加密部分、綜合數(shù)據(jù)的低熵區(qū)與高熵區(qū)特征。

5）在進行TLS加密通信時，應優(yōu)先選擇帶有AES＿GCM 或ChaCha20對稱密碼算法的密碼套件，以對抗基于隨機性特征的密碼體制識別攻擊。