質(zhì)量約束的三維模型建模方法

卜寧遠(yuǎn)　謝宇洋

摘? 要：在當(dāng)今的智能制造和工業(yè)軟件設(shè)計領(lǐng)域，CAD和CAE是極為重要的技術(shù)。但現(xiàn)有的CAD和CAE模型表示方法不統(tǒng)一，在數(shù)據(jù)交換上需要耗費大量時間，造成了計算資源極大的浪費。非均勻有理B樣條（NURBS）模型作為一種兼容CAD和CAE的模型表達(dá)方式，以樣條曲線為基函數(shù)，無須進(jìn)行交換即可進(jìn)行等幾何分析。本文提出了一種基于質(zhì)量約束的NURBS體建模方法，將模型質(zhì)量作為建模時的約束，使構(gòu)建的模型符合等幾何分析的要求。本文以帶有復(fù)連通域的模型為例進(jìn)行等幾何分析，經(jīng)過與主流商業(yè)軟件的對比，最小值相同，最大值誤差在10%以內(nèi)，運行時間減少了4.61%，驗證了此方法的正確性。

關(guān)鍵詞：NURBS;建模方法;等幾何分析

中圖分類號：TP391.41? ? ?文獻(xiàn)標(biāo)識碼：A

3D Modeling based on Mass Dependence

BU Ningyuan， XIE Yuyang

（School of Mechanical Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

BNY19971997@163.com; 826647688@qq.com

Abstract： CAD （Computer Aided Design） and CAE （Computer Aided Engineering） are extremely important technologies in today's intelligent manufacturing and industrial software design fields. However， representation methods of the existing CAD and CAE model vary， and it consumes a lot of time to exchange data， resulting in a great waste of computing resources. Non-uniform rational B-spline （NURBS） model， as a model expression compatible with CAD and CAE， takes spline curve as the basis function， and can perform isogeometric analysis without exchange. This paper proposes a NURBS modeling method based on mass dependence， which takes model mass as a constraint during modeling， so that the constructed model meets the requirements of isogeometric analysis. This paper takes a model with a complex connected domain as an example to perform isogeometric analysis. Compared with popular commercial software， the minimum value is the same， the maximum error is within 10%， and the running time decreases by 4.61%， which verifies the correctness of this method.

Keywords： NURBS; modeling method; isogeometric analysis

1? ?引言（Introduction）

隨著第四次工業(yè)革命的到來，多個國家都提出了工業(yè)數(shù)字化轉(zhuǎn)型的戰(zhàn)略規(guī)劃，在智能制造領(lǐng)域，關(guān)鍵之一就是工業(yè)軟件[1]。對于產(chǎn)品設(shè)計而言，專業(yè)的設(shè)計和仿真軟件是必不可少的。為了降低設(shè)計成本，減少設(shè)計時間，將設(shè)計（CAD）與分析（CAE）集成一體化已是大勢所趨。但迄今為止，CAD與CAE仍分為兩個獨立的領(lǐng)域[2]，因為采用的模型表達(dá)方式有所不同，導(dǎo)致兩者之間產(chǎn)生了縫隙。當(dāng)今主流CAD模型的表達(dá)多為邊界表達(dá)B-Rep[3]和構(gòu)造實體CSG[4]，而CAE模型為了適用于有限元分析（FEA）[5-6]，一般采用網(wǎng)格表示法。因此在整個設(shè)計與分析的過程中，模型會在CAD和CAE兩種表示方式之間反復(fù)切換，拓?fù)浣Y(jié)構(gòu)被破壞，模型精度明顯降低，時間成本大幅度提高[7-8]。

而NURBS參數(shù)化模型采用樣條曲線作為基函數(shù)，能精確表示邊界和曲面，且能提供模型內(nèi)部的連續(xù)性參數(shù)化表達(dá)式，無須進(jìn)行CAD和CAE之間的反復(fù)轉(zhuǎn)化，產(chǎn)生的模型能直接用來進(jìn)行等幾何分析。等幾何方法是有限元方法的繼承與發(fā)展，該方法采用樣條曲線作為基函數(shù)，具有較高的幾何精確性。

但是，體參數(shù)化模型為了適用于等幾何分析，必須要表示為零虧格的雙變量張量曲面或三變量張量體，且相鄰的體參數(shù)化單元之間的曲面要一致。因此需要對不滿足等幾何分析要求的體參數(shù)化模型進(jìn)行分割處理，且等幾何分析對模型的要求較高，分割后建立的模型還要在幾何上滿足等幾何分析的要求。

2? ?相關(guān)研究（Related works）

對于CAD和CAE融合，可以進(jìn)行CAD二次開發(fā)，在成熟的商業(yè)平臺上進(jìn)行融合;也可以使用重建法，在已知CAD模型邊界的基礎(chǔ)上得到內(nèi)部控制點的信息，但需要進(jìn)行大量的運算。體參數(shù)化建模不同于以上兩種，具有計算簡單、創(chuàng)建方便的優(yōu)點。

在CAD模型剖分方面，相關(guān)學(xué)者已做了大量工作。大致方向可分為兩種：（1）多邊形凸分解，將多邊形剖分為三角形、四邊形及任意凸多邊形集合;（2）網(wǎng)格分解，主要針對有限元模型，將CAD轉(zhuǎn)換為CAE形式表達(dá)，如狄利克雷三角剖分法。由于等幾何分析的特性，模型不需要再被轉(zhuǎn)換成CAE表達(dá)，因此體參數(shù)化剖分主要采用第一種思路。

常見的多邊形凸分解算法有兩種：（1）幾何單元區(qū)域剖分算法，如梯形分割算法[9];（2）考慮是否具有Steiner點的凸分解算法，如編碼劃分算法[10]和加權(quán)剖分算法[11]。但上述剖分算法僅在數(shù)學(xué)方面給出了多邊形分割方案，沒有考慮剖分結(jié)果是否符合分析標(biāo)準(zhǔn)，因此十分有必要評估四邊形質(zhì)量及其對等幾何分析結(jié)果的影響。

本文提出了一種以NURBS體參數(shù)化模型質(zhì)量為約束的建模方法，改進(jìn)了適用于等幾何分析的模型質(zhì)量評估方法，將模型質(zhì)量嵌入建模過程之中。首先遞歸分割模型截面，在分割過程中施加質(zhì)量約束，使分割后的截面滿足等幾何分析的要求;然后使用掃描、拉伸、旋轉(zhuǎn)、放樣等操作進(jìn)行體參數(shù)化映射，得到符合條件的體參數(shù)化模型。

3? 體參數(shù)化建模與模型質(zhì)量（Volume parametric modeling and model mass）

對于機械零件而言，大部分模型都可以定義截面及路徑，通過掃描、拉伸、旋轉(zhuǎn)、放樣等操作完成模型構(gòu)建。因此，為了使一般體參數(shù)化模型符合等幾何分析的要求，要先對截面進(jìn)行分割處理，將其分割成四邊形的集合，以滿足等幾何分析中雙變量張量曲面的要求。

3.1? ?截面剖分算法

本文使用的是遞歸剖分的方法，將整個模型控制點看作無向圖，采用深度優(yōu)先遍歷，逐層向下尋找合適的剖分方案。該算法時間空間復(fù)雜度與傳統(tǒng)算法相同，但在遞歸過程中加上了體參數(shù)建模所要求的約束，從數(shù)學(xué)問題轉(zhuǎn)化為工程問題，因此最終結(jié)果更符合等幾何分析的要求。

設(shè)算法輸入為多邊形子域集合POL，輸出為四邊形集合Quad，算法流程圖如圖1所示。

算法流程如下：

Step 1：若不為空，取作為，否則結(jié)束并返回。

Step 2：求解可行剖分線集合，設(shè)共有 種剖分連線方式，初始選擇剖分線。

Step 3：，表示該子域不滿足任何剖分條件;，表示已遍歷所有的剖分連線方式。如結(jié)果不滿足條件，則回溯至上一個剖分的子域，設(shè)為，。

Step 4：根據(jù)當(dāng)前選擇的剖分連線方式，創(chuàng)建一條新的NURBS曲線，同時獲得兩個新子域、，刪除當(dāng)前被剖分的子域。

Step 5：為凸四邊形，存入集合;為五邊形及以上，存入集合尾部;若均不符合，則回溯至上一個剖分的子域，。

Step 6：遞歸執(zhí)行Step 1至Step 5。

3.2? ?剖分中的模型質(zhì)量

在等幾何分析中，計算域的參數(shù)化對應(yīng)于有限元分析中的網(wǎng)格生成，對等幾何分析結(jié)果的準(zhǔn)確性是十分重要的[11]，需要將模型從物理域映射到參數(shù)域進(jìn)行分析。使用雅可比矩陣將模型從物理域映射到參數(shù)域，雅可比矩陣如下：

根據(jù)已有質(zhì)量理論，最標(biāo)準(zhǔn)的參數(shù)化模型應(yīng)滿足以下三個條件：（1）模型沒有自交;（2）等參單元盡可能正交;（3）等參單元盡可能均勻。這樣會使雅可比的值接近或等于1，參數(shù)域映射的效果最佳。而扭曲、自交、不均勻的曲面均會使雅可比的質(zhì)量變差從而破壞參數(shù)域映射，也會使等幾何分析求解偏微分方程的過程變得十分困難，因此在剖分中我們要盡量避免出現(xiàn)這種曲面。對于不合格的曲面，需要制定一系列檢測方法。

對于六面體網(wǎng)格，主流方法已經(jīng)給出了一系列檢測指標(biāo)：對角線度量、縮放雅可比、扭曲度和寬高比等。對于NURBS曲面而言，可以在曲面上取若干等參單元看作四邊形進(jìn)行質(zhì)量評估。我們在此選擇了區(qū)域面積A、寬高比asp和扭曲度dist三個指標(biāo)作為衡量四邊形的依據(jù)，以下是這三個指標(biāo)的詳細(xì)定義。

3.2.1? ?區(qū)域面積

如圖2所示，我們把每一個等參單元看作一個小的四邊形，為了衡量它是否均勻，是否接近最好的分析模型，我們首先定義邊向量，然后將其分為四個區(qū)域，定義坐標(biāo)軸。

其中，為四邊形的角點坐標(biāo)。為了衡量四個角點區(qū)域是否在統(tǒng)一平面上，定義每一個角點處的法向量：

為了方便計算，設(shè)它們的單位向量：

定義一個中心法向量作為全局的法向量和單位向量，分別為：

將整個區(qū)域按照坐標(biāo)的上下左右軸分成四塊，如圖3（a）所示，則可以根據(jù)已知的參數(shù)求得每塊的區(qū)域面積：

根據(jù)幾何知識可以知道，若（即該四邊形某一區(qū)域的面積）小于0，則該片一定是退化的，如圖3（b）所示，即為凹四邊形。

對于NURBS曲面而言，由于邊界是曲線，因此直接按照角點求法向量是沒有意義的，但每個面的控制點和等參線可以構(gòu)成若干個小的等參單元。等參單元最好的情況是四條邊兩兩正交，而退化的等參單元一定不滿足邊邊正交，因此會拉低整體的圖形質(zhì)量。因此，所有等參單元面積大于0的數(shù)量越多越好。當(dāng)凹四邊形出現(xiàn)時，必然會有一個區(qū)域面積等于或小于零。凹多邊形的出現(xiàn)使得等幾何分析中的參數(shù)域映射和求解偏微分方程的效果很差，是一定不能出現(xiàn)在分析模型之中的，因此利用區(qū)域面積法可以很簡單地判別出不符合情況的條件之一，且與普通四邊形剖分中的射線法相比更具有魯棒性。

3.2.2? ?寬高比

NURBS等參單元的結(jié)構(gòu)越均勻越好，因此可以定義高寬比來評價等參單元是否均勻：

其中，A為四邊形面積，寬高比值域為，經(jīng)驗表明為可接受域。寬高比排除的是看起來很“窄”的四邊形，這類四邊形的出現(xiàn)會使控制點的分布極其不均勻，導(dǎo)致等幾何參數(shù)域的映射效果很差，也是一種不能出現(xiàn)在體參數(shù)化模型上的情況之一。寬高比的求解只需要在區(qū)域面積的基礎(chǔ)上再加上一步運算即可，消耗的資源很少，產(chǎn)生的效果卻很好。

3.2.3? ?扭曲度

為了衡量四邊形是否扭曲，首先要建立一個參照系，設(shè)一個位于坐標(biāo)原點的正方形的面積;再根據(jù)式（3）可以算出所有高斯積分點的最小雅可比值，則扭曲度定義為：

扭曲是衡量從參數(shù)空間到世界坐標(biāo)映射行為的良好程度的一種度量，值域為，越接近1效果越好，因此將可接受域設(shè)為。

根據(jù)以上三個指標(biāo)，可以較為準(zhǔn)確地檢查剖分截面的均勻性、正交性和扭曲度，且計算也十分簡單，不會占用太多時間和空間。這幾個指標(biāo)可以在遞歸時的判別條件中加入，在連接分割線后，依次檢查這三個值，若有不在接收域的情況則不合格，否則放入備選庫，作為可能的選項之一。

3.3? ?體參數(shù)化映射

得到了剖分好的NURBS四邊形曲面后，可以使用掃描、拉伸、旋轉(zhuǎn)、放樣等操作進(jìn)行體參數(shù)化映射。拉伸體模型可以通過截面控制點沿直線方向的仿射變換得到，在CAD中多用于凸臺等結(jié)構(gòu)的創(chuàng)建。如果模型的路徑不是直線而是圓弧，則可以進(jìn)行旋轉(zhuǎn)體映射。若拉伸的路徑不是直線也不是規(guī)則圓弧，則可以用掃掠體造型。

對于無法用一個截面生成的模型，可以考慮采用放樣體造型，沿曲線路徑插值放樣體的造型方法和掃掠體相似，需要先統(tǒng)一各個截面的階數(shù)、節(jié)點矢量及控制點數(shù)量，確保截面與該點曲線切矢垂直，再通過反求控制點即可得到沿曲線路徑的放樣體。而不沿路徑插值的放樣方式則無須保證各截面與曲線切矢垂直。

對于機械零件而言，大部分模型都可以通過這幾種建模方法得到。在得到了體參數(shù)化模型之后便可以直接進(jìn)行等幾何分析，而不需要再花大量時間進(jìn)行網(wǎng)格劃分。

4? ?實例（Examples）

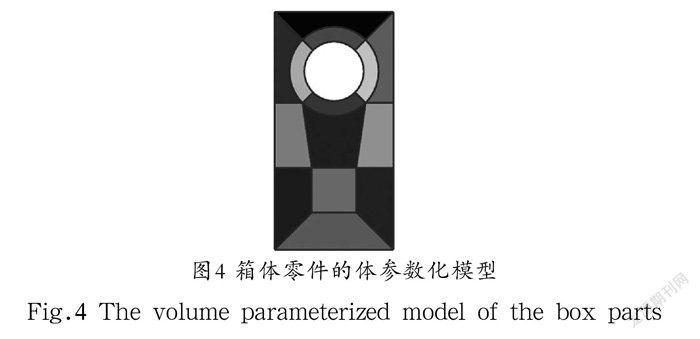
本部分以一個帶有通孔的箱體配件為例，該配件經(jīng)常用于減速箱上，頂部受力，底部有固定約束，是典型的機械部件之一。我們在其上表面施加力約束，下表面固定，進(jìn)行靜力學(xué)分析。由于配件帶有通孔，因此進(jìn)行剖分之前需要在圓上插入若干的點，再進(jìn)行剖分，且圓孔周圍的分割線也要保持一定的弧度以免與圓相交，再進(jìn)行拉伸操作，最后得到的體參數(shù)化模型如圖4所示。再使用MATLAB軟件對模型進(jìn)行等幾何分析，得出的結(jié)果與ANSYS軟件對比如表1和圖5所示，位移的最小值相同，最大值相差在10%以內(nèi)，同時平均運行時間減少了4.61%，證明了本文方法的有效性。

5? ?結(jié)論（Conclusion）

本文為CAD和CAE的無縫集成提供了一種新的思路，即以NURBS樣條曲線模型代替原有的CSG和B-Rep模型，這樣使得進(jìn)行分析的時候無須數(shù)據(jù)格式和表達(dá)方式的轉(zhuǎn)換，大大降低了時間復(fù)雜度和內(nèi)存空間的消耗。本文以箱體配件為例，展示了如何對帶有復(fù)連通域的圖形進(jìn)行剖分和建模，經(jīng)過與商業(yè)軟件的對比得到了較好的結(jié)果。

但此方法仍然存在一些問題。等幾何分析對模型的要求較高，一些不規(guī)則圖形如點陣材料等還無法通過簡單的掃描、拉伸、旋轉(zhuǎn)、放樣等簡單的體參數(shù)化映射方法得到。同樣的，對于一些細(xì)微的特征如倒角、圓角和小孔等也無法完全保留，這也是我們下一步主要研究的方向。另外，為了提高體參數(shù)化建模保留原有幾何特征的能力，使構(gòu)建的模型更加精確，對體參數(shù)化模型布爾運算也需要進(jìn)一步研究。

參考文獻(xiàn)（References）

[1] 寧振波.力筑工業(yè)之基重鑄智造靈魂[J].軟件導(dǎo)刊，2021，? 20（01）：7-11，6.

[2] SMIT M S， BRONSVOORT W F. Integration of design and analysis models[J]. Computer-Aided Design and Applications， 2009， 6（6）：795-808.

[3] KIM B C， MUN D. Feature-based simplification of boundary representation models using sequential iterative volume? ?decomposition[J]. Computers & Graphics， 2014， 38：97-107.

[4] 羅月童，樊曉菁，俞盛朋，等.基于面殼封閉的B-Rep至CSG轉(zhuǎn)換算法[J].計算機輔助設(shè)計與圖形學(xué)學(xué)報，2014，26（10）：1673-1680.

[5] AVERSA R， PETRESCU F I T， PETRESCU R V V， et al. Biofidel FEA modeling of customized hybrid biological hip joint design part Ⅱ： Flexible stem trabecular prostheses[J]. American Journal of Biochemistry and Biotechnology， 2016， 12（4）：23-29.

[6] KASIK D J， BUXTON W， FERGUSON D R. Ten CAD challenges[J]. IEEE Computer Graphics and Applications， 2005， 25（2）：81-92.

[7] PARK H S， DANG X P. Structural optimization based on CAD-CAE integration and metamodeling techniques[J].Computer-Aided Design， 2010， 42（10）：889-902.

[8] PAN Z， WANG X， TENG R， et al. Computer-aided design-while-engineering technology in top-down modeling of mechanical product[J]. Computers in Industry， 2016， 75： 151-161.

[9] 王金敏，劉季燁，方沂.基于梯形分解的不規(guī)則多邊形干涉算法[J].工程圖學(xué)學(xué)報，2005（06）：52-57.

[10] 肖忠暉，盧振榮，張謙.簡單多邊形凸單元剖分的編碼算法[J].計算機學(xué)報，1996（06）：477-481.

[11] 王博，李笑牛，李華.一種加權(quán)剖分簡單多邊形為三角形和凸四邊形子域的算法[J].中國圖象圖形學(xué)報，2002，7（005）：? ?486-490.

作者簡介：

卜寧遠(yuǎn)（1997-），男，碩士生.研究領(lǐng)域：CAD/CAE.

謝宇洋（1997-），男，碩士生.研究領(lǐng)域：CAD/CAE.