函數教學的幾點思考

許作飛

函數是初中數學教學的重點也是難點，教師教學時應幫助學生梳理函數的知識網絡，并將其融入整個初中數學知識體系中。函數圖像的解讀可以幫助學生深化理解函數的概念，提高學生的識圖能力，增強學生數形結合的解題意識。在函數學習中，要指導學生運用數形結合思想探討函數問題的解題策略，運用數學建模思想培養學生的應用意識，提高學生解決函數類問題的技巧。

初中數學中，一次函數、反比例函數和二次函數三個單元學習的側重點雖不同，其解決問題的方法和經驗其實是相通的，教學時應打好基礎穩步推進。指導初中生學習函數，得從函數的概念出發，引導學生循序漸進地深入探究，理清函數的知識網絡，并將其融入整個初中數學知識體系之中，使學生對函數知識融會貫通。

函數學習中，入門很重要，多數學生對函數學習產生困惑都是因為對“函數”概念的理解不清晰。筆者在函數入門教學時，先通過具體的實例，讓學生初步了解函數，學生初步感受函數后，再從函數概念的角度規范它，從例題學習中辨識并鞏固它。

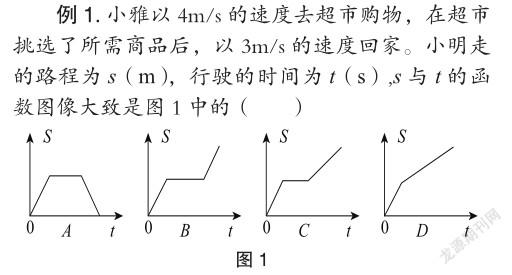
分析：解讀本題函數圖像，必須搞清楚各選項之間的區別，準確理解各選項中每一段函數圖像的實際意義。A、B、C三個選項中都有一段與橫軸平行的線段，而D選項中沒有。線段表示時間在變化而航行的路程沒變，正與題意在超市選商品，停留一段時間不吻合，故D選項被排除在外。圖中B、C、D三個選項的圖像只有起點在橫軸上，而A選項除了起點外，還有一個點在橫軸上。有的學生從“從家出發又返回家”這個角度理解它，誤認為選A。此時，可引導學生討論縱軸表示的含義——小明走的路程，而不是“離家的距離”，所以A選項應被排除在外。到這里剩下B和C兩個選項了，B選項的第一段和第三段是平行的，而C選項的第一段和第三段不平行。小明往返的速度不同，所以這兩條線段應該不平行。B被排除，本題選C。

選用函數圖像進行解讀，盡量選取選擇題作為例題，降低學生學習難度，借助對函數圖像的解讀，幫助學生掌握一些有關函數圖像的常識，提高他們解讀函數圖像的能力，增強他們數形結合的意識。運用對函數圖像的解讀，深化學生對函數概念的理解，是函數教學不可或缺的步驟。如果僅僅對課本中的函數圖像進行解讀，圖像的類型及數量遠遠不夠。教學時，筆者從智學網上選擇一些函數圖像，讓學生合作探究、討論、交流，理解其含義。

函數本身比較抽象，有的問題還需要學生根據條件自己畫圖，要求學生熟練掌握各類函數圖像的特征，解題時若能結合圖形理解，往往便能一目了然。解決函數問題，既要依據條件中數量，又要根據圖像信息進一步分析數量之間的關系，做到數形結合。

1.一次函數

一次函數是基本的函數類型，學習一次函數時，不僅要讓學生強化一次函數的知識技能，還要向學生滲透函數學習的一般常識，比如求函數圖像與坐標軸的交點坐標，求兩個函數圖像交點的坐標，判定一個點是否在某個函數圖像上等，注重用數形結合的數學思想解決一次函數的問題。

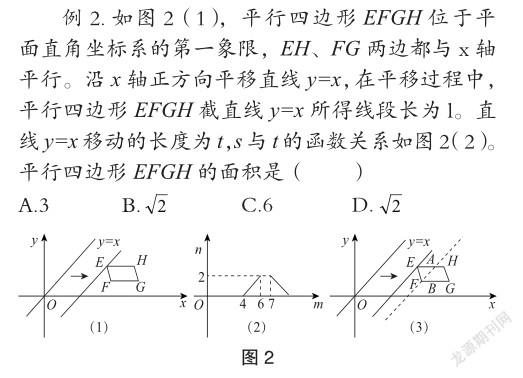
2.反比例函數

反比例函數的學習要充分借鑒解一次函數的經驗，注意區別兩類函數間的區別，反比例函數的圖像是雙曲線，其增減性與一次函數完全不同，教學時引導學生區分清楚。

解決反比例函數問題，通常都涉及函數圖像，雖然圖像未必要畫出來，但心中要有清晰的印象，利用圖像解決問題。

3.二次函數

二次函數的圖像是拋物線，y=ax2+bx+c（a≠0）的開口和方向由“a”決定，圖像的位置由“b”和“c”決定；y=a（x-k）2+h（a≠0）的圖像中，“k”和“h”決定了圖像的頂點坐標。

例4.將拋物線y=-x2+6x-5在x軸下方的部分沿x軸翻折到x軸的上方，得到如圖4（1）的圖像。一條動直線y=x+b與這個圖像恰好有3個公共點，求b的值。

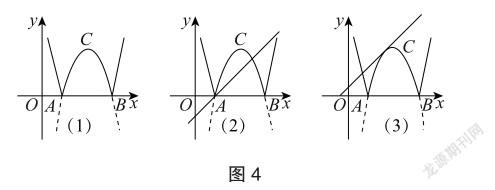
分析：動直線y=x+b與y=x平行，當“b”很小時，它們沒有交點，將其向上平移經過點B時，兩者有一個交點，繼續向上平移時出現兩個交點，當它經過點A時，恰有三個交點，如圖4（2）。繼續向上平移則有四個交點，當兩個函數圖像相切時，如圖4（3），又恰有三個交點，再向上平移就是有兩個交點了。顯然在兩種情況下，直線y=x+b與變化過的二次函數圖像恰好有3個公共點。

本題中，求直線y=x+b與這個圖像恰好有3個公共點時b的值，靠苦思冥想是得不出結論的，必須根據題目的條件，畫出草圖，根據圖形，分析在什么情況下有3個公共點，再用方程思想解決問題，離開數形結合解本題是比較困難的。

建模是很重要的數學思想，一方面，學生有時在解決實際問題時不知所措，而相應的數學問題常常能駕輕就熟，通過建模搭建橋梁可以讓學生順利解題。另一方面，函數的一般式、數學公式等其實也都是建模的思想在解題中的運用。數學建模，有利于深化學生的函數思想。

用數學模型解決實際問題，使數學學習不再抽象，降低了初中生學習函數的難度，促進了學生數學核心素養的提升。