基于卷積神經網絡的冗余機械臂運動學逆解求解

劉世平， 夏文杰， 陳 萌， 馬梓焱， 黃元境， 張文奇

(1.上海市空間飛行器機構重點實驗室， 上海 201108； 2.華中科技大學機械科學與工程學院， 武漢 430074)

1 引言

對于自由度數目小于7 的非冗余機械臂，通過所期望的末端位置和姿態信息，可使用幾何解法對其運動學逆解進行求解，得到機械臂的各個關節角度來控制機械臂的運動。 與非冗余機械臂相比，冗余機械臂具有許多優良的性能，如增加機械臂靈活度、實現避障、具有良好的容錯性等，但是其求解運動學逆解的過程更加復雜。

幾何解法和數值解法是目前主要的7 自由度機械臂運動學逆解的求解方法。 幾何解法具有求解速度快、求解精度高等優點，但是其通用性差，主要適用于符合Pieper 準則的特殊構型機械臂，通過給定臂形角，增加約束的方法進行求解。目前傳統數值解法有加權最小范數法、廣義/狹義雅克比偽逆法、梯度投影法等，這些方法具有良好的通用性，但是計算量大、求解時間較長、存在累積誤差，并且當機械臂處于奇異位置時，無法對其運動學逆解進行求解。

為克服傳統方法的不足，智能算法在冗余機械臂運動學逆解求解問題中得到應用，這些算法主要采用遺傳算法、神經網絡等。 Xia等通過雙神經網絡完成了對冗余機械臂的控制；Toshani 等通過將神經網絡與非線性二次規劃相結合進行7 自由度機械臂逆解的求解；歐群文等首先通過遺傳算法獲得7 自由度冗余機械臂運動學逆解的樣本數據，然后使用RBF(徑向基)神經網絡對樣本進行訓練得到運動學逆解解法；Demby 等使用人工神經網絡和自適應神經模糊推理系統對4、5、6 和7 自由度機械臂的運動學逆解進行了求解。

卷積神經網絡 ( Convolutional Neural Networks， CNN)在獲取數據特征方面得到廣泛的應用。 本文基于某型7 自由度機械臂的運動學模型，對LeNet 模型進行改進，設計卷積神經網絡對機械臂運動學逆解的問題進行求解。

2 卷積神經網絡模型搭建

對該7 自由度機械臂構型連桿坐標系進行建立，坐標系如圖1 所示。 DH 參數表如表1 所示。

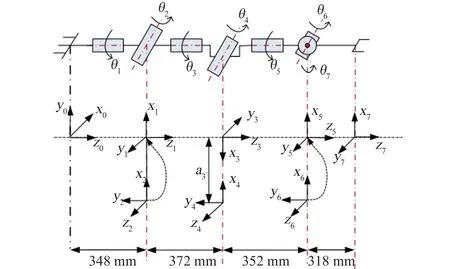
圖1 7 自由度機械臂DH 坐標系Fig.1 DH coordinates frames of the 7－DOF manipulator

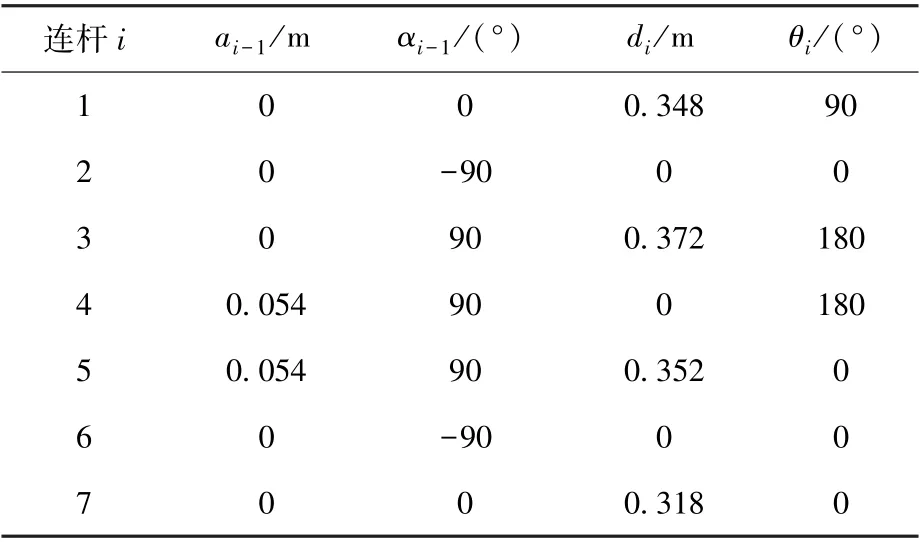
表1 7 自由度機械臂DH 參數Table 1 DH parameters of the 7－DOF manipulator

各關節角度與末端位姿的關系如式(1)、式(2)所示。

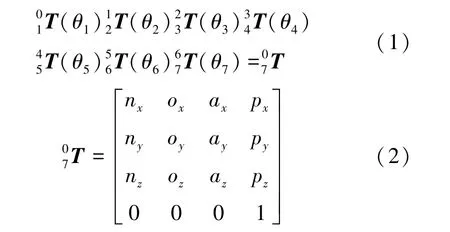
式中，θ為第關節角度， T(θ) 為第1關節到第關節之間的變換矩陣，＝1，2，…，7。

機械臂的末端位姿矩陣是通過7 個關節角計算得出，具有對應關系，因此可以對神經網絡模型輸入末端位姿矩陣來計算機械臂相應的關節角角度。 在本文建立的卷積神經網絡模型中，輸入層為3× 4 的位姿矩陣，包括3× 3 的旋轉矩陣與1× 3 的平移矩陣；輸出層為7 個神經元，代表機械臂各個關節角度。

2.1 卷積核

數據的特征可以通過卷積核進行卷積操作獲得。 由于所給的輸入層是3×4 的矩陣，并且該矩陣以列向量作為特征，所以輸入層選用的卷積核大小為3× 1，通過卷積核可以組合列向量的值，如式(3)所示。

2.2 激活函數

激活函數可以讓線性輸入變為非線性輸出，通過不同的神經元個數以及激活函數可以完成映射關系的實現。 目前激活函數有多種，常用的有函數、函數以及函數。 由于函數相對于其他2 種激活函數的計算復雜度低、收斂速度快，并且不容易出現梯度消失與梯度飽和等問題，因此本模型選用的激活函數為函數，如式(4)所示。

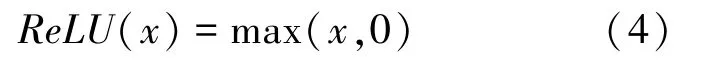
2.3 損失函數

在模型訓練中，需要衡量模型所得到的預測值與真實值之間的誤差，在機器學習中，將衡量誤差大小的函數稱為損失函數。 通常損失函數的值是正的，其值越大表示得到的模型的訓練誤差越大。 平方誤差函數與交叉熵損失函數是目前比較常用的損失函數。 交叉熵損失函數通過計算得到輸出層的每個神經元預測值在0 到1 之間，因此一般用于分類問題中。 平方誤差函數直接得到預測值與真實值的誤差，可以用于函數擬合，所以損失函數使用平方誤差函數，見式(5)。

2.4 優化算法

根據已經給出的損失函數，為了求得最小化損失函數的值，需要通過優化算法有限次迭代神經網絡模型參數來盡可能降低損失函數的值。 目前神經網絡使用較多的優化算法有SGD 算法、Adam 算法等。 SGD 算法雖然可以達到全局最優，但是該算法需要自己設定學習率，對學習率的設定很嚴格，并且容易在模型訓練過程中停在鞍點，而Adam 算法不用人為設定干預學習率且容易跳過鞍點。 該模型所選用的優化算法為Adam算法。

2.5 卷積神經網絡模型結構設計

卷積神經網絡能夠保留數據輸入的形狀從而較好地得到數據的特征。 LeNet是一個具有5層網絡結構的CNN 模型，含有2 個卷積層、3 個全連接層及2 個池化層。 2 個卷積層卷積核大小為5× 5，輸出通道數為6 和16，3 個全連接層的輸出個數為120，84 和10，最后一層的10 代表模型的輸出種類個數，LeNet 已經成功用于手寫數字的識別。

本文對LeNet 模型進行改進設計，模型總共設計7 層，前3 層結構為卷積層，后4 層的結構為全連接層，由于每一層輸入的數據尺寸較小且卷積核較小，因此該模型不包含池化層，并且增大卷積層輸出通道數以增加訓練的參數，增強擬合能力。

模型的輸入層是3×4 的矩陣，輸入層的卷積核為3× 1，輸出通道數為64，對矩陣每一個列向量的特征進行學習，下一層的卷積核為1× 1，輸出通道數為64，第3 層卷積核為1× 4，輸出通道數為256，第3 層對前一層數據的所有特征進行學習。 后4 層全連接的輸出個數分別為256、128、64 和7，最后一層輸出數7 表示7 自由度機械臂的各個關節角角度。

為防止模型對某些神經元過度依賴，造成模型過擬合問題，可以在不改變輸出期望值的情況下對模型使用丟棄法，隨機丟棄一些神經元。 該模型在第3 層與第4 層使用了丟棄法，丟棄概率為0.1。

3 卷積神經網絡模型訓練

本文建立的卷積神經網絡如圖2 所示，模型的輸入信息為7 自由度機械臂的位姿矩陣，輸出值為7 自由度機械臂各個關節角角度，訓練集為10 000組數據。 該卷積神經網絡的訓練過程如下:

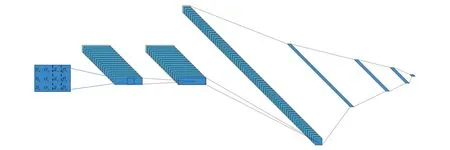
圖2 卷積神經網絡模型Fig.2 Convolutional neural networks model

1)參數初始化設置。 由于偏置對于神經網絡中的梯度流動并無影響，神經網絡偏置初始化為0。 但是當神經網絡初始權重也置為0 時，正向計算時所有狀態值與激活值的結果為0，同時反向計算時所有梯度為0，那么對于整個神經網絡訓練過程而言，相當于梯度消失了，不能進行任何有效的訓練。 神經網絡的訓練過程中是基于梯度下降進的，因此參數的均值為0，輸出和輸入數據的方差一致訓練效果更好，可以通過對初始參數進行高斯分布或均值分布達到該目的。 He等考慮了激活函數對輸出數據分布的影響，其正態分布初始化以0 為中心，標準差為式(6)。

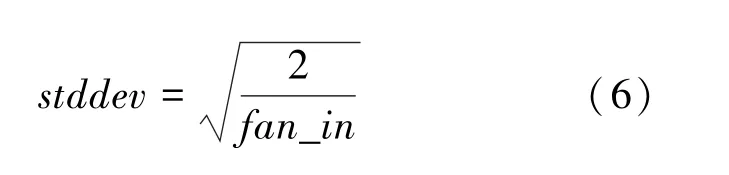
式中，＿為權重張量中輸入單位的數量。

該模型選用的激活函數為函數，因此神經網絡初始權重初始化方法為He 等的方法。 為了得到較快的訓練速度與較好的訓練精度，模型的＿設置為64，設置為160。

2)正向傳播與反向傳播。 數據沿著神經網絡模型的結構進行正向傳播，依次計算并存儲模型的中間變量，通過正向傳播得到的輸出值與真實值的平方差計算得到單個樣本的損失函數，為了防止過擬合，同時計算范數正則化對模型的權重參數進行約束，得到總的損失函數為式(7)、式(8):

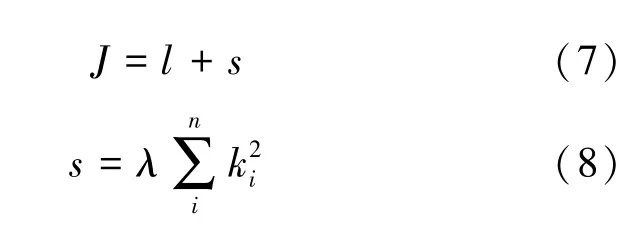
式中，為總的損失函數，為單個樣本損失函數，為對權重參數范數正則化的值，的取值影響約束程度，k為權重參數。

通過反向傳播，從輸出層到輸入層，依據鏈式法則計算神經網絡中參數的梯度，并對參數進行更新，最終得到卷積神經網絡的模型。

3)實驗配置與訓練結果。 本文使用的開發語言為python3.7，深度學習平臺為tensorflow2.0，GPU 為NVIDIA GeForceGTX 950M，CPU 為Intel Core i5－6300HQ。 通過為160 次的訓練得到卷積神經網絡的損失值如圖3 所示，在訓練過程中最后損失值接近于0，訓練能夠收斂，訓練效果較好。

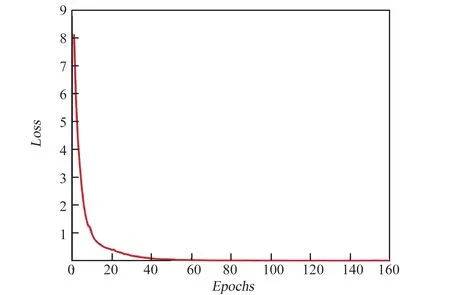
圖3 卷積神經網絡訓練過程中損失值Fig.3 Loss value in convolution neural networks training

4 實驗驗證

為驗證所設計模型對7 自由度機械臂運動學逆解求解的準確度與有效性，通過設計軌跡跟蹤實驗進行驗證。 實驗內容為:通過給定期望軌跡，用卷積神經網絡求出7 自由度機械臂的各關節角度值，用所求得的角度通過運動學正解得到機械臂末端的運動軌跡，最后得到與期望軌跡誤差值。所定義的機械臂的期望軌跡為式(9):

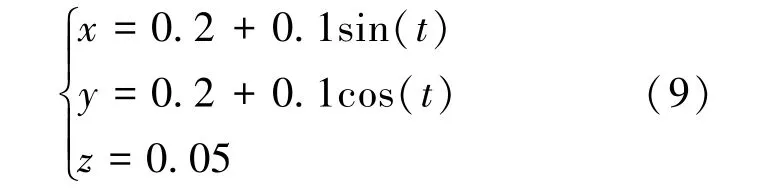
從軌跡中選取66 個點的位姿信息輸入卷積神經網絡模型中求運動學逆解得到各個關節角度如圖4 所示，所計算的關節角范圍在機械臂的給定范圍內，并且計算得到的各關節角角度的曲線為光滑曲線，因此機械臂的運動為連續運動。

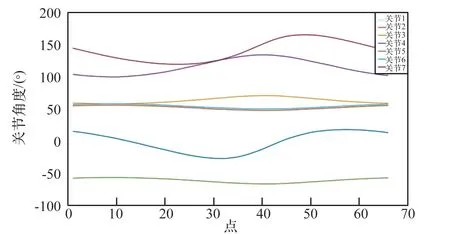
圖4 機械臂各關節角角度曲線Fig.4 Angle curve of each joint angle of manipulator

把機械臂關節角角度通過運動學正解得到末端軌跡圖，如圖5 所示，基于卷積神經網絡所求得的軌跡與期望軌跡基本重合，因此使用該方法進行機械臂運動學逆解求解得到的結果較好。

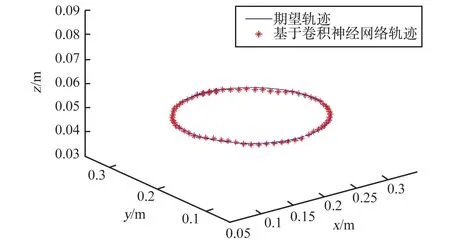
圖5 軌跡對比圖Fig.5 Comparison of the trajectories

同時，根據機械臂運動學正解的結果獲得本模型求解過程中實際軌跡點與期望軌跡點各個方向的誤差值與總體誤差值，分別如圖6 與圖7 所示。 從圖6 中得出所求實際軌跡點與期望軌跡點在各個方向上的誤差在2.5 mm 以內，從圖7 中得出總的誤差在3 mm 以內，平均誤差為1.2 mm。模型求解的誤差在實際任務中能夠滿足所需的運動要求。 本方法求解的時間為12.96 ms，而使用該機械臂自帶的粒子群算法計算時間為428 ms，使用傳統的梯度投影法計算時間為637 ms，本方法在計算時間上得到了明顯提高。 通過對軌跡跟蹤實驗的誤差分析表明所設計的模型能夠用來求解7 自由度機械臂運動學逆解，并且具有一定的求解精度與較短的求解時間，滿足所執行實際任務的需求。

圖6 實際軌跡與期望軌跡各個方向誤差Fig.6 Error of the actual trajectory and expected trajectory in all directions

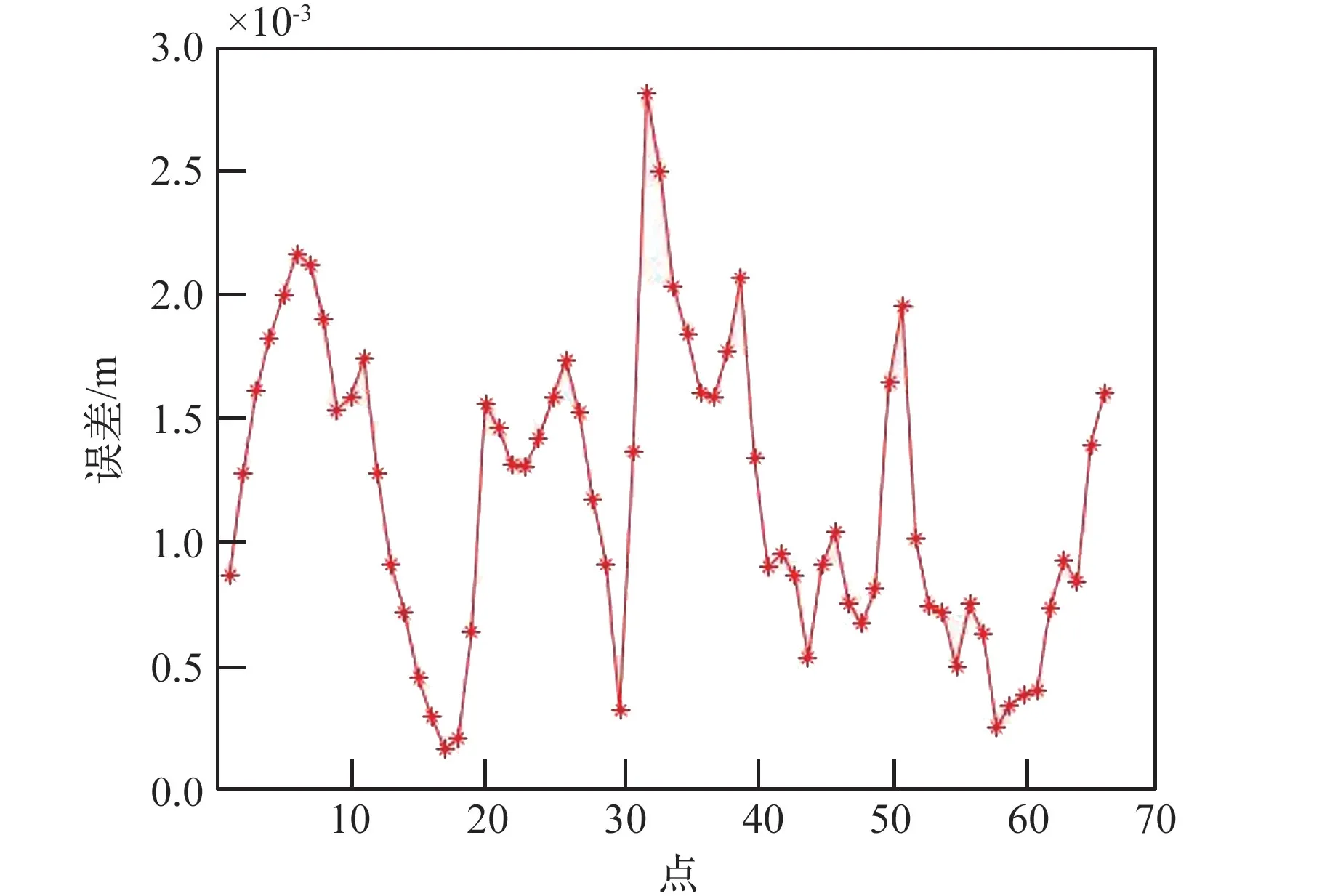
圖7 實際軌跡與期望軌跡總誤差Fig.7 Total error between actual trajectory and expected trajectory

5 結論

本文針對7 自由度冗余機械臂運動學逆解的求解問題，設計了卷積神經網絡模型進行求解，得到機械臂運動軌跡到各個關節角度之間的映射關系。 通過對LeNet 模型進行改進，對卷積核、激活函數、損失函數、優化算法、模型結構與初始參數等進行設計與選擇，建立了符合7 自由度機械臂運動學逆解求解問題的卷積神經網絡模型。 最后設計了軌跡跟蹤實驗對所建立的卷積神經網絡模型的有效性和求解精度進行驗證，結果表明使用卷積神經網絡對機械臂運動學逆解問題求解方法有效。