用于光纖傳感的改進變分模態分解-DWT算法

邵向鑫,路天麒,馬子筱,江 虹,馬柯異

(1.長春工業大學電氣與電子工程學院,吉林 長春 130012；2.東北電力大學自動化工程學院,吉林 吉林 132012)

1 引 言

光纖布拉格光柵(Fiber Bragg Granting,FBG)被作為傳感元件用于測量溫度、應變力等物理量。在橋梁、地鐵、結構健康監測等工程中得到廣泛的應用[1]。

對于大容量FBG傳感網絡測量系統來說,在采集光纖光柵傳感信號的過程中通常會因人為、環境等因素產生噪聲,對信號本身造成干擾。最大限度的去除噪聲,保持解調信號的精確至關重要。變分模態分解(Variational Mode Decomposition,VMD)在2014年首次提出[2]。它克服了經驗模態分解(Empirical Mode Decomposition,EMD)模態混疊頻繁出現以及提取固有模態函數(Intrinsic Mode Functions,IMF)時缺乏數學理論的缺點。擁有良好的基礎理論并對噪聲樣本具有更強的魯棒性。VMD的主要問題之一是算法運行之前需設置模態函數IMF的分解層數K。高的K值可能會導致模式混合,而低的K值可能會導致模式重復[3]。

本文采用一種可以連續提取所有IMF的分解方法,在不需要知道模態數量也可以完成信號分解并結合具有強大時頻分析能力的改進小波閾值函數用于處理光纖傳感信號。

2 改進的變分模態分解算法

變分模態分解VMD是一種自適應、完全非遞歸的模態變分和信號處理的方法,改進變分模態分解(Improved Variational Mode Decomposition,IVMD)的關鍵問題在于對分解獲取的本征模態函數分量進行約束。

IVMD是通過在VMD的基礎上添加一些約束條件以避免收斂到先前提取的模式。能夠自適應的確定模態數的同時減少了一些不必要的計算量,加快了計算速度。

設輸入信號f(t)分解為兩個信號:第K個模式uK(t)和殘余信號fr(t),即:

f(t)=uK(t)+fr(t)

(1)

其中,殘余信號fr(t)包含兩個部分:先前獲得的模式之和(∑i=1:K-1ui(t))以及信號未處理部分(fu(t))；

(2)

為了減少計算量提高計算速度及避免模態混疊等現象的發生,定下4條約束條件使∑i=1:K-1ui(t)=0。

(1)每種模式應在其中心頻率附近保持緊湊。故第K個模式最小化約束為:

(3)

其中,ωK是第K模式的中心頻率;*表示卷積運算。

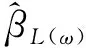
(4)

(3)通過同樣的方法建立條件約束J3:

(5)

(4)重建信號f(t):

(6)

其中,α是用于平衡J1,J2和J3的參數,最后通過對偶上升法(Dual Ascent)求出拉格朗日乘數λ(t)的更新公式:

(7)

3 可調節半軟閾值去噪

小波軟閾值、硬閾值理念最早于1995年由Donoho教授等人提出,函數定義于公式(8)、(9)；

(8)

(9)

小波閾值因其強大的時頻分析能力一經提出就得到廣泛應用。但是傳統的軟、硬閾值函數存在恒定偏差大,連續性差的缺點。為了提高算法性能,學者們引入調節因子α,提出一種軟硬閾值折中的閾值函數改善此類問題[4]。改進后的閾值函數取得了良好的效果,但是由于函數不能高階可導,導致重構信號在臨界閾值λ處曲線不夠平滑。

針對以上問題,本文提出一種新閾值函數:

(10)

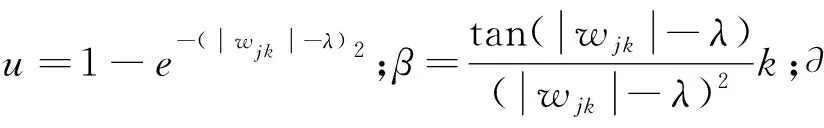
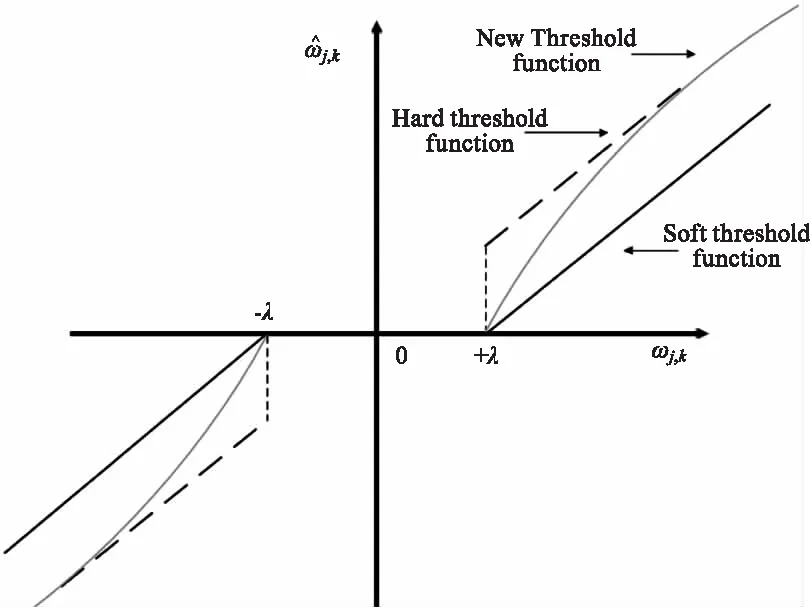
圖1 函數示意圖

由于噪聲的小波變換系數會隨著尺度的增大而減小,本文采用一種可以隨分解層數變化而變化的自適應閾值:

(11)

其中,j為分解尺度；N為各層小波變換系數長度；σ為噪聲的方差。

新閾值函數高階可導,同時在wj,k=±λ處保持連續。ωj,k隨著閾值函數取值的增加越來越接近硬閾值函數。很好地解決了閾值與小波系數間存在恒定偏差的問題。

4 改進變分模態分解-DWT算法

基于小波分解-EMD方法的成功應用[5],本文方法首先將輸入的原始信號進行模態分解,得到BLIMF分量,然后對BLIMF進行小波分解并用本文閾值函數對信號進行處理,最后進行小波逆變換重構信號。流程圖如圖2所示。

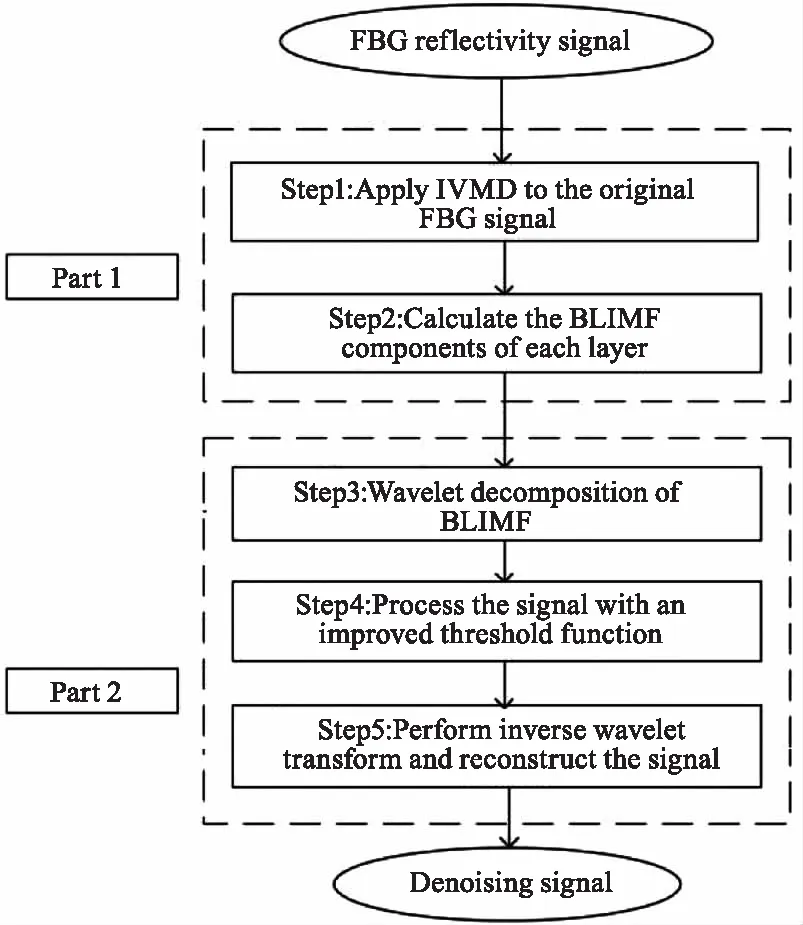
圖2 總體流程圖

經過自身的實驗與前人的研究[6],選擇sym5作為小波基,小波分解層數為6。VMD參數選擇如下:平衡參數α=200收斂準則的公差tol=1×10-7。

5 實驗及分析

5.1 算法實驗及分析

利用MATLAB軟件測試效果,對一段中心波長為1550 nm的反射譜加入5 dB高斯白噪聲模擬含噪環境,對信號進行軟閾值、硬閾值、小波閾值-EMD[7]以及本文方法進行對比實驗。通過信噪比(SNR)和均方根誤差(RMSE)來鑒定去噪效果。公式如(12)、(13):

(12)

(13)

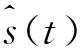
從圖3可以較直觀地看到四種方法的去噪效果。硬閾值函數去噪后的信號存在偽吉布斯現象,含有較多震蕩點。相比較而言軟閾值函數去噪后的波形震蕩點較少,但是重構信號失真比較大。小波閾值-EMD方法取得了良好的效果,消除了大部分噪聲信號,與之相比本文方法取得了最好的去噪效果,保留了最多的信號特征。

圖3 不同方法對FBG信號去噪對比

表1和表2列出了四種方法在5 dB到25 dB含噪環境下處理信號的信噪比(SNR)與均方根誤差(RMSE)實驗數據。圖4以折線圖的方式較直觀地展現了不同方法對FBG信號去噪后的RMSE趨勢。

表1 不同方法對FBG信號去噪后的信噪比

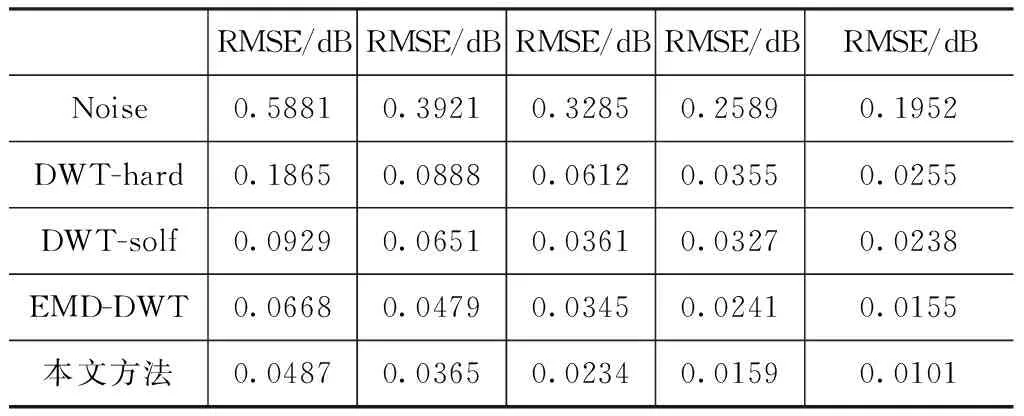
表2 不同方法對FBG信號去噪后的均方根誤差

圖4 不同方法對FBG信號去噪后的RMSE

新的模態分解不僅解決了選取K值過大或過小導致的模態混疊問題,而且計算復雜度在高模態下遠低于VMD算法,如圖5所示。

圖5 不同模態數需計算量

5.2 溫度測試實驗

為了驗證本文提出方法在FBG解調系統中的應用效果,采用傳感光柵進行溫度測量實驗[8]。實驗平臺采用光源參數:500～2400 nm,輸出功率為100 mW；光譜儀為橫河 AQ6370D-12-L1H/FC/RFC 光譜分析儀,波長掃描范圍為1550 nm波段的中心波長。

實驗將FBG傳感器放入與外界隔絕的恒溫槽中從5～60 ℃每間隔5 ℃調節一次溫度,并測中心波長,每個溫度點測量5次,取其平均值。測量結果如表3所示。

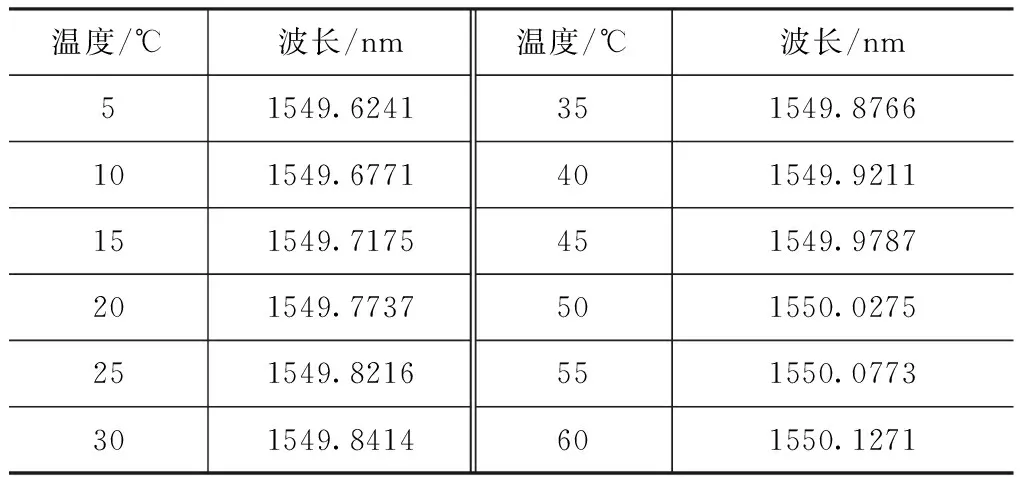
表3 不同溫度下的布拉格波長

對實驗數據進行擬合得到溫度與波長的關系,如圖6。測量數據的線性相關系數R=0.9992,說明溫度與波長具有良好的線性關系,能滿足實際工程需求。

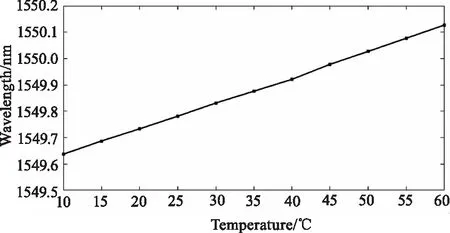
圖6 波長與溫度關系曲線

6 結 語

本文在VMD算法的基礎上添加了4個約束條件使其能夠自適應的提取K值,并在高模態下大大減少了其計算量,然后在軟、硬閾值函數以及文獻[5]的基礎上構造一種新的閾值函數用于處理FBG信號,提高的去噪效果。在MATLAB仿真實驗上引入信噪比(SNR)和均方根誤差(RMSE)進行對比,信噪比相比于軟、硬閾值函數及當前去噪方法均有所提高,均方根誤差均有降低。最后通過溫度測試實驗表明此方法具有良好的線性關系,能夠滿足實際工程需求,具有一定應用價值。