汽車傳動系扭振激勵辨識與減振措施*

曲俊龍，史文庫，陳志勇

（吉林大學，汽車仿真與控制國家重點實驗室，長春 130022）

前言

汽車傳動系扭轉振動對整車NVH 性能有重要影響。當傳動系統的扭轉模態被激勵，傳動部件將發生劇烈的轉速波動，不僅會造成車內振動與噪聲水平升高，還有可能加速傳動部件的疲勞斷裂與損壞。因此，在汽車產品投入市場前，應先消除傳動系扭振帶來的隱患。

國內外的學者針對這一問題做了許多研究。文獻［1］中建立了3 自由度非線性傳動系模型，以較高精度模擬了扭振的發生頻率與共振峰值，并通過增加離合器的摩擦阻尼抑制傳動系扭振；文獻［2］中研究了萬向節不等速傳動引起的傳動系扭振問題，通過嘗試減小萬向節的交角并引入柔性聯軸器來抑制扭振；文獻［3］中研究了雙質量飛輪在不同工況下的減振作用，并分析了不同參數對雙質量飛輪減振效果的影響；文獻［4］中在傳動系引入慣量盤來改變傳動系扭振的頻率；文獻［5］中通過降低半軸的扭轉剛度減小了傳動系扭振，降低了車內的轟鳴噪聲；文獻［6］中研究了變頻扭轉動力吸振器組在降低傳動系扭振方面的應用，并對其最佳調諧頻率進行了研究；文獻［7］和文獻［8］中通過結合試驗與仿真研究了變速器產生敲擊聲的機理，并通過調節離合器扭轉減振器的剛度和阻尼特性來抑制敲擊的產生。

然而，在上述研究中，均未涉及如何在缺少發動機缸壓曲線的情況下，以較高的精度進行轉矩激勵的建模與傳動系扭振仿真。在進行傳動系扭振仿真時，如果缺少了缸壓曲線，則只能對轉矩激勵進行簡化建模。這時研究人員則只能通過反復調整模型來逼近試驗曲線，導致時間成本增加，且通常會帶來較大的仿真誤差。本文中為解決這一問題展開研究，以某樣車存在的傳動系扭振問題為例，進行道路試驗，接著建立4 自由度非線性傳動系扭振模型；提出一種缸壓曲線的擬合函數，并通過參數辨識獲得缸壓曲線和發動機激勵轉矩；然后，對模型進行時域仿真，驗證模型準確性；最后通過調整結構參數并增設慣量盤，移除常用轉速段的傳動系扭振。

1 傳動系扭振試驗

試驗樣車是一臺搭載4 缸4 沖程柴油機的4×2輕型載貨汽車。樣車在以5 擋加速行駛過程中，在1300～1700 r/min 的發動機轉速段內發生強烈的振動和異響，引起駕駛員腿部發麻和壓耳感。初步考慮是發動機的2 階波動轉矩激起了傳動系的扭轉模態，引發了傳動系扭振。因此，對樣車進行實車道路試驗，在飛輪、變速器輸入端、變速器輸出端和后橋輸入端布置了轉速傳感器，在駕駛員的座椅導軌和右耳旁分別布置了振動加速度傳感器和傳聲器。利用LMS 數據采集前端設備對信號進行采集，采樣頻率為50 kHz，頻域分辨率為1 Hz。采集后，利用Simcenter. Testlab. 18 軟件進行數據處理，試驗結果如圖1～圖3所示。

從圖1 可看出，傳動系轉速曲線在1560 r/min附近出現劇烈波動，樣車加速過程中轉速波動以2階為主，存在扭轉共振，共振中心頻率為52.0 Hz。其振動特點為：以離合器為分界點，在離合器后端的傳動部件發生扭振，且振幅相近。此外，如圖2 和圖3 顯示，在同一轉速范圍內2 階分量幅值突出，因此確定車內異常振動和噪聲是由傳動系扭振引起的。

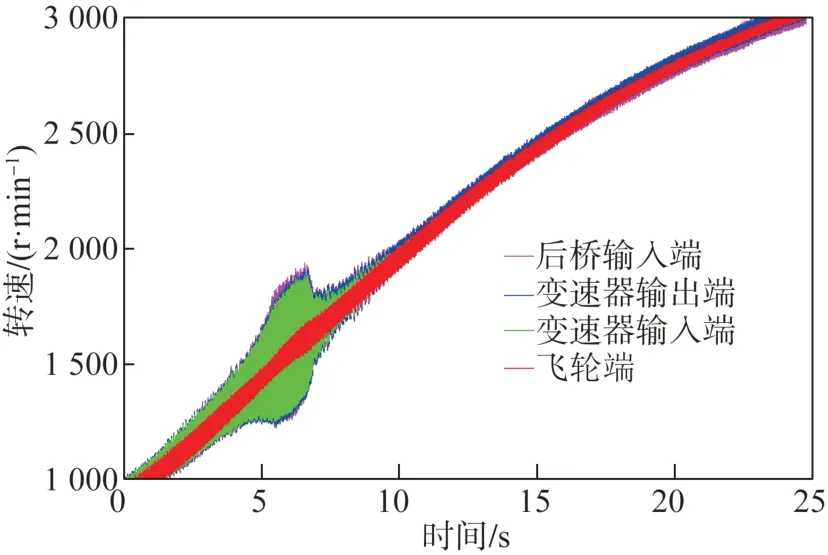
圖1 試驗轉速曲線圖

圖2 試驗座椅導軌振動colormap圖

圖3 試驗駕駛員右耳噪聲colormap圖

2 動力傳動系統扭振模型

2.1 傳動系模型

汽車動力傳動系是一個復雜的非線性系統，為能描述和預測其在不同工況和不同設計參數下的動力學性能，須對真實系統進行合理簡化，建立一個有限自由度的模型。因此，本文中將樣車動力傳動系簡化為一個4 自由度的集中質量模型，模型示意圖如圖4所示。

圖4 傳動系扭振模型示意圖

根據簡化模型可建立微分方程：

式中：為發動機等效轉動慣量與飛輪轉動慣量之和；為變速器、傳動軸和后橋的等效轉動慣量之和；為車輪等效轉動慣量；為車身等效轉動慣量（～皆為按速比等效至發動機曲軸的轉動慣量）；～為對應～的轉角；為離合器扭轉減振器扭轉剛度；為半軸扭轉剛度；、分別為扭轉減振器和半軸的等效黏性阻尼系數；為發動機激勵轉矩；為車輪驅動轉矩；為行駛阻力矩；為總機械傳遞效率。

2.2 發動機激勵轉矩

發動機激勵轉矩主要由3 部分組成，即氣體轉矩、慣性轉矩和摩擦轉矩。對于單缸發動機來說，激勵轉矩可表示為

其中，氣體轉矩是由發動機氣缸內可燃混合氣燃燒膨脹產生高壓，并作用于活塞傳至曲軸產生；慣性轉矩是由活塞與連桿做往復運動時的慣性力換算而來；摩擦轉矩則由多種摩擦力組合而成。根據力學與運動學關系，可得到氣體轉矩和慣性轉矩表達式：

式中：為活塞位移；為曲柄半徑；為連桿長度；=/；為曲軸轉角；為連桿擺角；為氣缸壓力；為氣缸直徑；m為單缸等效往復運動質量。對于摩 擦 轉 矩T的 計 算，采 用Rezeka-Henein 模 型實現：

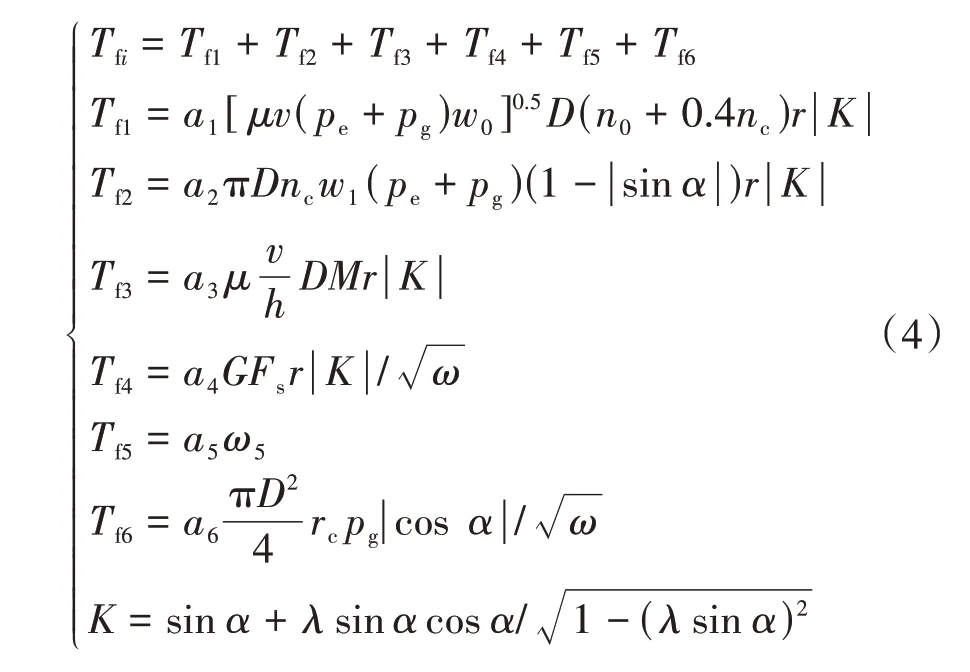
式中：為活塞環黏性摩擦轉矩；為活塞環混合摩擦轉矩；為活塞裙摩擦轉矩；為氣門機構摩擦轉矩；為附件與非承載軸承摩擦轉矩；為承載軸承摩擦轉矩；為轉矩換算系數。其余參數的具體含義請參見文獻［12］。因此，對于四缸發動機而言，其總激勵轉矩為各缸激勵轉矩之和：

2.3 輪胎模型

汽車在加速行進過程中，輪胎與地面之間并非時刻保持相對靜止，而是存在一定的滑轉。輪胎滑轉的存在將會影響其與地面之間縱向力的大小，進而影響汽車的加速過程。因此，對輪胎滑轉特性進行建模是必要的。本文中將輪胎看成彈性體，其滑轉的產生不僅與輪胎及地面的相對運動有關，還與胎體的變形有關。該輪胎模型用公式表述為

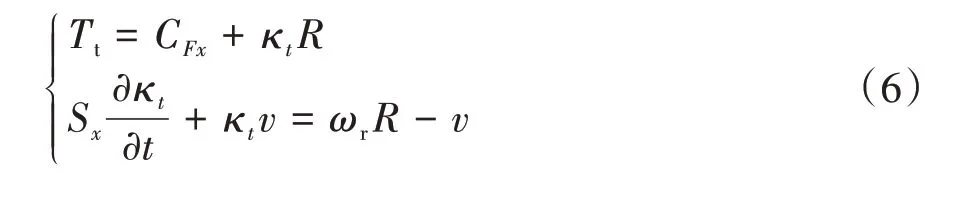
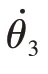
2.4 行駛阻力

汽車的行駛阻力矩用公式可表示為

式中：為滾動阻力；為風阻；為空氣阻力系數；為迎風面積；為空氣密度；為汽車總質量；為滾動阻力系數，隨車速增加而變大。

2.5 傳動效率

汽車內部阻力主要來源于動力傳動系運轉時的機械損耗，可以用傳動效率來描述。總傳動效率可由各部件傳動效率相乘求得

式中：為離合器傳動效率；為變速器齒輪嚙合效率，由于5 擋為直接擋，故在此取1.0；為萬向節傳動效率；為后橋綜合傳動效率；為包括滾動軸承等其他非承載部件綜合傳動效率。參數具體值見表1。其中，慣量、剛度、阻尼及結構參數值是由樣車三維模型提取或試驗測得，其余部分參數值采用文獻參考值或由經驗公式算得。

表1 仿真參數

3 發動機激勵辨識

汽車發動機激勵轉矩的建模方法一般分為3種，即解析法、試驗法和諧波法。解析法是通過模擬發動機循環燃燒發生的物理過程，建立熱力學和流體力學方程來描述發動機的輸出特性。該方法的計算精度較高，但需要的發動機參數過多，且模型建立較為復雜，耗費計算資源，不適用于傳動系扭振分析；第2 種為基于試驗數據的方法。利用試驗獲得的發動機缸壓曲線計算燃燒力，結合活塞與曲柄連桿機構的力與運動關系，得到作用在發動機曲軸上的激勵轉矩。該方法簡單直觀，僅須考慮發動機輸入輸出關系而不必了解內部物理過程。但由于獲取發動機缸壓曲線需要進行大量試驗，對試驗設備要求較高，試驗周期長且耗資較多，成為運用該方法的一個阻礙；第3 種是諧波疊加法，即將發動機的激勵轉矩看成由平均轉矩與多個諧波共同組成。該方法簡單方便，但高階諧波數據仍需要試驗數據支持，若僅用低次諧波數據又會導致發動機缺少中高階的轉矩激勵，使激勵信號存在一定程度的失真。

這里主要針對如何基于扭振試驗數據獲取發動機缸壓曲線展開討論。

3.1 發動機缸壓曲線擬合分析

四沖程柴油機的一個燃燒周期包括進氣、壓縮、做功和排氣4 個沖程，其缸壓曲線表現為以曲軸每旋轉兩周即每720°為一個周期的周期性信號。因此，截取柴油機低速工況缸壓曲線的一個周期進行分析，如圖5所示。

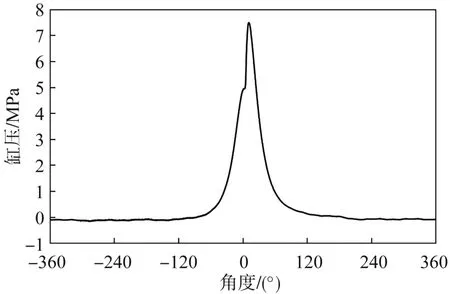
圖5 缸壓曲線

從圖5 可見，缸壓曲線中曲軸每旋轉180°，發動機氣缸內完成一個沖程。其中在壓縮和做功沖程，發動機缸內壓力急劇上升，達到最高缸壓后又迅速降低，而在進氣和排氣階段，缸壓保持在大氣壓附近。通常，車用四沖程柴油機均具有上述特點。

試驗測得的發動機缸壓信號是一系列的離散點，然而辨識一系列離散點是難以實現的。若想對發動機的缸壓進行辨識，須提取發動機缸壓曲線的共同特征，搭建合適的擬合函數。故嘗試采用不同類別的擬合函數對上述發動機缸壓曲線進行擬合，擬合效果如圖6 所示，擬合精度如表2 所示，其中為誤差平方和，為確定系數，為均方根誤差。

圖6 3種擬合函數對比

表2 各函數擬合精度

從圖6 可見，8 階多項式函數不能逼近缸壓曲線。而2 階高斯函數和8 階傅里葉函數可以在整個周期內較好地逼近缸壓數據，但由于8 階傅里葉函數變量多于2 階高斯函數，辨識難度更大，且精度小于2階高斯函數，因此選用2階高斯函數作為缸壓曲線的擬合函數，其表達式為

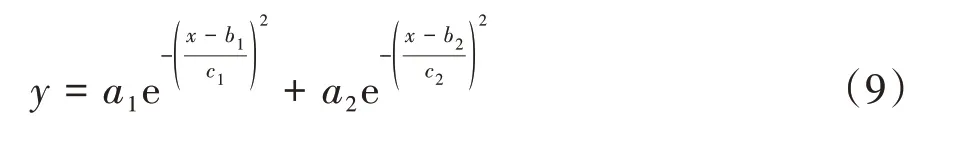
其中參數、控制函數的幅值，參數、控制函數的峰值位置，參數、控制函數的分布范圍。此外，發動機在燃燒循環過程中氣缸內存在負缸壓時刻，而高斯函數無法表示負值，因此在2 階高斯函數的基礎上增加一個常量項，作為最終缸壓曲線的擬合函數。

3.2 發動機缸壓曲線辨識

如式（10）所示基于2 階高斯函數的缸壓擬合函數具有7 個未知量，為獲得試驗工況下樣車發動機的平均缸壓曲線，須結合試驗數據與所搭建傳動系模型對上述7 個未知參數進行辨識。缸壓曲線擬合參數的辨識流程如圖7所示。

在新時期實踐中我們發現學生核心素養的培養和提升受到高度重視。在實踐中新教學理念和方法的出現為教學的發展插上騰飛的翅膀，使得教學氛圍得到極大的改善，學生在英語閱讀中敢于大聲的去朗讀，使得自身英語學習水平在不斷的提升，同時學生在日常生活中勇于使用英語去交流，在實踐中學生的英語口語能力在不斷的提升。此外我們發現學生的英語寫作能力也得到不斷的提升，總之，從整體上看學生英語核心素養得到不斷的提高。

圖7 缸壓參數辨識與傳動系扭振仿真流程圖

辨識過程采用遺傳算法進行迭代尋優。遺傳算法是一種智能優化算法，通過模擬自然界種群的繁衍與進化，融入優勝劣汰的選擇機制，經過多輪迭代，最后收斂到最優解。在進行參數辨識時，將樣車發動機轉速從1000 加速到3000 r/min 所用時間作為優化目標，以仿真加速時間與實際加速時間的1000 倍差方作為個體適應度函數，以保證優化結果的誤差量級在0.001 s 以內。適應度函數為

式中：為仿真加速時間；為試驗測得實際加速時間。

最終參數辨識結果如圖8所示。辨識在第68代達到收斂條件，即平均適應度值變化小于1×10，最優適應度值在18 代開始就已收斂到0，說明遺傳算法適用于該模型的參數辨識，能夠很快收斂到最優解。

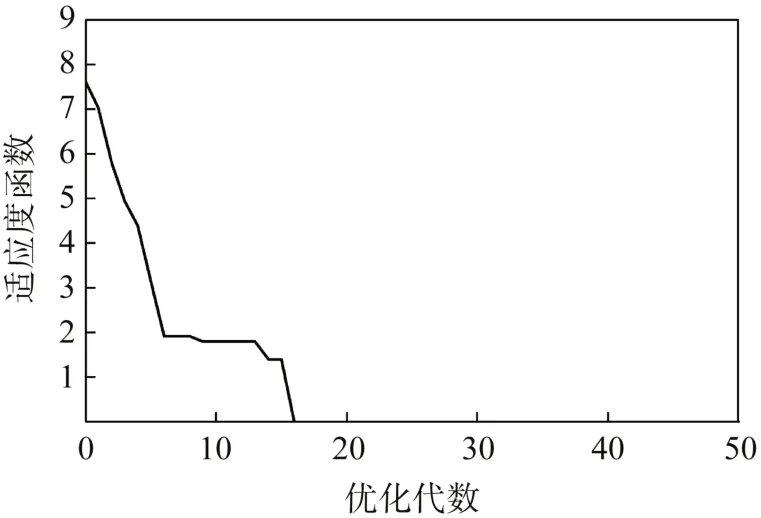
圖8 遺傳算法迭代收斂曲線

式（10）的參數辨識結果如表3 所示。并繪制曲線如圖9 所示。最終的缸壓辨識結果與生產廠家提供的該加速工況下平均峰值缸壓13.92 MPa 相比，其峰值誤差為-2.82%。

圖9 辨識所得缸壓曲線

表3 擬合函數參數辨識結果

將辨識所得的曲線作為各缸的缸壓曲線代入式（2）～式（5），計算獲得樣車在加速工況下發動機一個工作循環的瞬態合成激勵轉矩，如圖10所示。

圖10 發動機瞬時激勵轉矩

4 仿真結果與模型驗證

在獲得發動機的激勵轉矩后，將其代入到4 自由度非線性傳動系模型，利用MATLAB/SIMULINK進行編程搭建，采用4 階龍格庫塔法對運動微分方程進行數值求解，步長為0.0001 s，獲得的仿真結果如圖11～圖14所示。

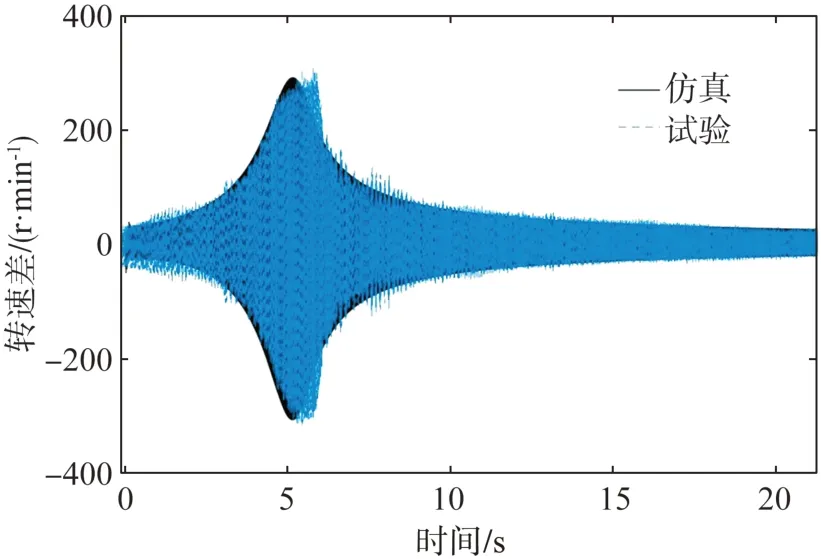
圖11 仿真時域轉速波動

圖11 為離合器兩端相對轉速的仿真與試驗對比。可見在整個加速過程中仿真與試驗結果重合良好。在加速過程中，離合器兩端的相對轉速具有一定波動，這是由于離合器扭轉減振器存在減振彈簧。而其中相對轉速在5 s 左右出現峰值，則表示離合器后端傳動系出現了較大的轉速波動，這是樣車傳動系統發生了扭轉共振的表現；圖12～圖13 對比了試驗與仿真的變速器轉速colormap 圖。可見圖中均以2階轉速波動為主，在1300～1700 r/min之間均出現轉速波動峰值；提取圖12 與圖13 中的2 階轉速切片繪制成圖14。從圖中可知，仿真與試驗結果相比，共振峰頻率誤差為1.03%，幅值誤差為2.91%，說明利用本文提出的模型與辨識方法進行仿真，能夠以較好的精度還原試驗結果，可用于傳動系扭振的研究和后續的優化分析。

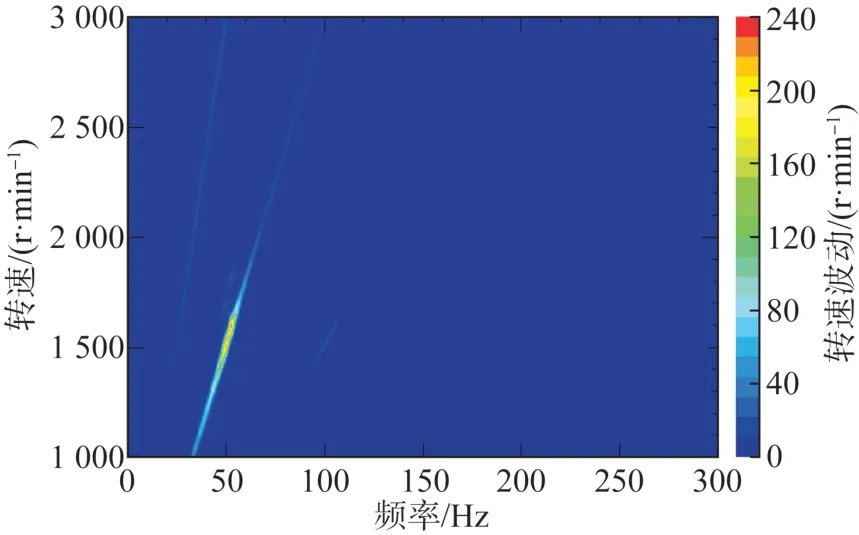
圖12 試驗轉速colormap圖

圖13 仿真轉速colormap圖

圖14 轉速2階切片對比

5 傳動系扭振改進

在振動力學中，對共振的抑制方法主要有兩類。第一類為從振源上消除振動，即通過移頻手段將共振頻率移出常用工作區間，或通過引入阻尼來抑制共振峰值，或增設動力吸振器來衰減振動；第二類為在振動的傳遞路徑上隔離振動。即在振動的傳遞路徑上設置減振結構，或應用吸振、阻尼材料降低振動的能量傳遞。考慮到減振措施的穩定性與耐久性，采用移頻的方法，通過調整離合器扭轉減振器與半軸的剛度，以及在傳動軸處增設慣量盤，將傳動系扭振的固有頻率移到常用車速下發動機的激勵頻率之外。

在不影響轉矩傳遞的情況下，將離合器扭轉減振器的彈簧剛度降為原來的50%，半軸剛度降為原來的70%，并在傳動軸末端靠近后橋處增設一個轉動慣量為0.02 kg·m的剛性慣量盤，以實現移頻的目的。對改進前后的傳動系統進行模態分析與計算，所得結果如表4所示。由表可知，改進后系統的扭振頻率降為34.40 Hz，即共振轉速被降至1032 r/min，說明傳動系的扭轉固有頻率被移至常用轉速范圍之外，同時也并無其它共振頻率引入到激勵頻率范圍內。此外，將更改后的系統參數代入扭振模型進行求解，得到加速工況下傳動系時域轉速曲線如圖15 所示。從圖15可知，在1160～2320 r/min 范圍內，傳動系在加速過程中沒有出現轉速曲線鼓包，在整個常用加速區間不再出現傳動系統扭振現象，符合移頻要求。

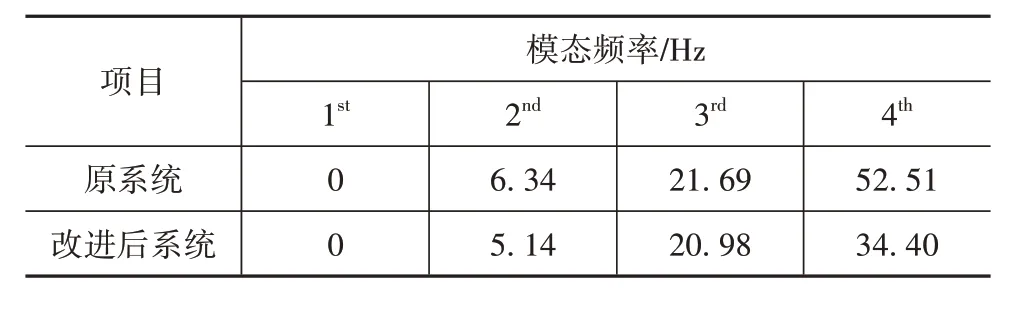
表4 模態分析結果

圖15 改進后轉速曲線

6 結論

（1）構造了基于2 階高斯函數的發動機缸壓曲線擬合方程，并利用遺傳算法對缸壓擬合方程的未知參數進行辨識，將辨識結果代回擬合方程，獲得樣車加速工況的缸壓曲線，與實際缸壓參數相比，辨識精度良好。

（2）建立了傳動系統4 自由度扭轉振動模型，考慮了發動機的激勵轉矩、摩擦轉矩和車輪滑轉等非線性因素對加速工況扭振的影響。將擬合缸壓曲線代入模型，利用龍格庫塔法進行數值求解。仿真與試驗結果的相對誤差較小，驗證了模型的正確性與精確度。

（3）通過降低離合器與半軸的扭轉剛度并在傳動軸處增設慣量盤，將傳動系固有頻率移出該擋常用轉速范圍外，解決了樣車加速過程中的傳動系扭轉共振問題。