扁平流線型箱梁渦激振動雷諾數效應研究

劉慶寬， 任若松， 孫一飛， 李 震， 鄭云飛

(1. 石家莊鐵道大學 省部共建交通工程結構力學行為與系統安全國家重點實驗室，石家莊 050043；2. 河北省風工程和風能利用工程技術創(chuàng)新中心，石家莊 050043；3. 石家莊鐵道大學 土木工程學院，石家莊 050043； 4. 石家莊鐵路職業(yè)學院 鐵道工程系，石家莊 050043)

風對橋梁的作用包括靜力作用和動力作用，其中，動力作用主要是指顫振、馳振、渦激振動和抖振等風致振動，危害非常嚴重，受到廣泛關注。渦激振動是一種發(fā)生在低風速下的常見振動，國內外許多橋梁都曾發(fā)生過明顯的渦激振動，例如加拿大的Lion Gate橋[1]、英國的Second Severn Crossing[2]等。渦激振動雖然不會造成橋梁在短期內垮塌，但可能導致結構的疲勞損傷，影響橋梁的正常使用，還有可能引起其他附屬構件的破壞[3]。因此，有必要對渦激振動的相關特性開展研究，以明確渦激振動的發(fā)生條件、振動規(guī)律、影響因素和激發(fā)機理等。

風洞試驗是橋梁抗風研究的主要方法之一，但由于風洞本身的限制，風洞試驗可以實現的雷諾數與結構實際雷諾數存在較大差異，所以，試驗結果與實際結果可能存在一定偏差。Schewe等[4]利用增壓風洞實現了實橋級別的雷諾數，發(fā)現在低雷諾數下得到阻力系數高于高雷諾數下的結果，證實了雷諾數效應的存在。鮮榮等[5]對某扁平流線型懸索橋的不同尺度的節(jié)段模型進行了渦激振動試驗，結果發(fā)現大比例尺模型的渦激振動振幅比小比例模型的振幅要小。而崔欣等[6]在扁平流線型橋梁的渦激振動試驗中發(fā)現大比例尺模型的渦激振動振幅較大。董浩天等[7]對某懸索橋的不同尺度的節(jié)段模型以及全橋模型模型進行了風洞試驗，發(fā)現增大模型尺度后渦激振動的鎖定區(qū)間變窄并提前，渦激振動的振幅降低。胡傳新等[8]對扁平流線型橋梁的兩種比例尺節(jié)段模型進行了同步測振、測壓風洞試驗，發(fā)現高雷諾的渦振響應大于低雷諾數，且渦激振動的起振風速低于低雷諾數。

總之，國內外的學者對扁平流線型橋梁斷面渦激振動的雷諾數效應進行了研究，但通常僅選用了兩個雷諾數進行對比試驗，且試驗結果之間存在差異，為了進一步研究扁平流線型箱梁渦激振動的雷諾數效應，探究渦激振動發(fā)生機理，本文針對某一扁平流線型箱梁，研究了三種雷諾數下風攻角與渦激振動特性和風壓分布的關系，探討了不同雷諾數下的風壓分布對于渦激振動的雷諾數效應的貢獻。

1 風洞試驗

風洞試驗在石家莊鐵道大學風工程研究中心STDU-1風洞的低速試驗段進行，試驗段寬4.4 m，高3 m，可實現風速范圍1.5～30 m/s，紊流度≤0.4%。選取某一實際斜拉橋的扁平流線型箱梁作為研究對象，主梁寬32 m，高3.5 m，寬高比為9.14，風嘴角度為57°。考慮試驗段、主梁尺寸和阻塞度的要求，確定模型縮尺比為1∶55，模型寬0.58 m，高0.064 m，長1.16 m。模型以鋼管和加勁肋板為骨架，外覆ABS板材，保證模型具有足夠的剛度。在模型的1/2截面處布置了1圈測壓點，測壓點數量為150，尖角部位流動更加復雜，該部位的測壓點進行適當加密。模型及測壓點布置示意圖如圖1所示。主梁模型通過兩端的剛臂分別連接4根彈簧，彈簧則固定在風洞外的剛性框架上，模型兩端還安裝了0.82 m×0.19 m的矩形端板，以消除端部的影響[9]，安裝好的彈性模型系統如圖2所示。

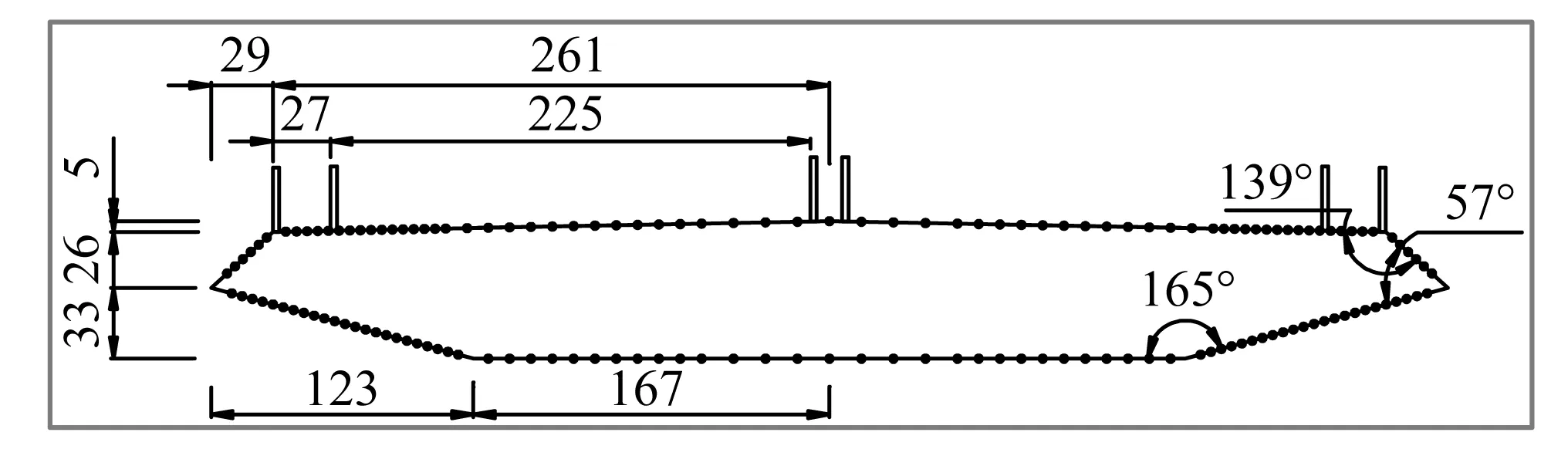
圖1 模型及測壓點布置示意圖(mm)Fig.1 Model and pressure measuring point layout(mm)

圖2 彈性模型系統Fig.2 Elastic model system

風攻角α定義為來流方向與模型上下表面分界線之間的夾角，當來流方向與分界線重合時，風攻角為α=0°。模型順時針轉動，風攻角增大，反之減小，試驗風攻角為α=+5°,α=+3°,α=0°,α=-3°和α=-5°。

雷諾數表征的是流體的慣性力與黏性力之比，可以通過式(1)計算。

(1)

式中：U為來流風速；D為模型特征尺寸，此處取為模型高度；ρ為空氣的密度；μ為空氣的動力黏性系數；ν為空氣的運動黏性系數。

為了研究渦激振動的雷諾數效應，通過更換模型兩端的彈簧，得到三套具有不同自振頻率的模型系統，依次進行試驗，進而得到不同雷諾數下的渦激振動。三次試驗分別記為試驗(1)、試驗(2)和試驗(3)，通過自激試驗得到三套模型的自由衰減曲線，利用FFT變換得到頻譜，如圖3所示，進而計算出自振頻率和阻尼比，三套模型的自振頻率分別為3.4 Hz，5.5 Hz和8.2 Hz，阻尼分別為0.12%，0.11%和0.11%。

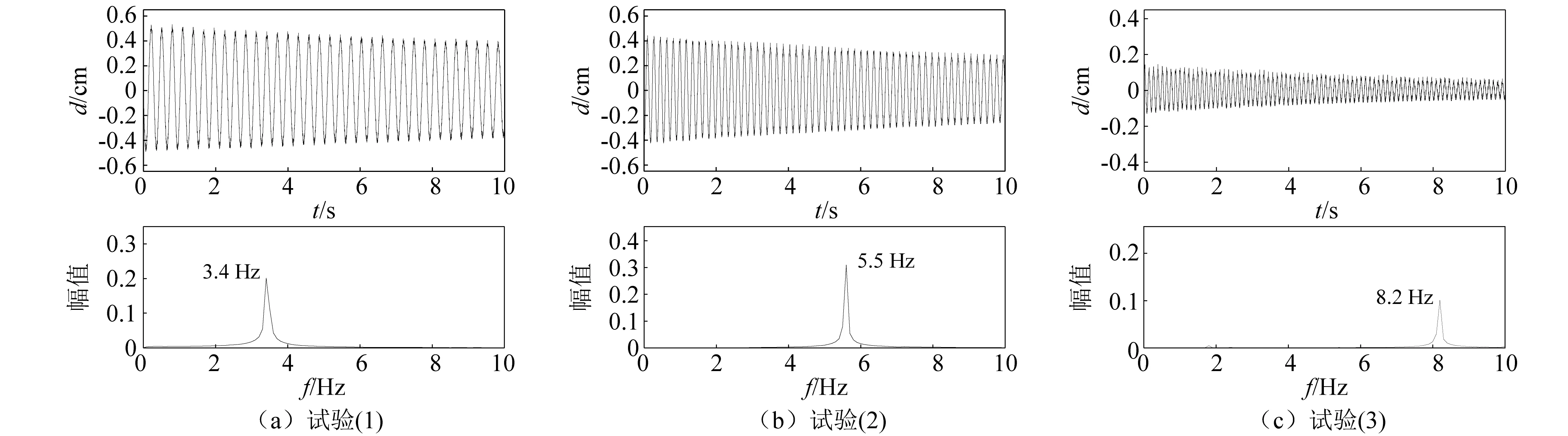
圖3 模型自由衰減曲線及頻譜Fig.3 Model free attenuation curve and spectrum

2 試驗結果及討論

為了便于分析模型表面的風壓分布規(guī)律，現針對模型表面測壓點，定義了一種無量綱距離。

Dd=d/D

(2)

式中：d為沿測壓點所在表面從測壓點到A點的距離；D為沿測壓點所在表面從B點到A點的距離，部分測壓點無量綱距離示意如圖4所示。

圖4 測壓點無量綱距離示意圖Fig.4 Dimensionless distance diagram of pressure measuring point

2.1 主梁渦激振動特性及雷諾數效應

三組試驗在α=+5°和α=+3°均出現了明顯的振動，而在其他風攻角下沒有發(fā)現明顯的振動。對α=+5°下的位移時程和頻譜圖進行分析，發(fā)現振動為單一頻率的限幅振動，振動頻率與自振頻率一致，且振動僅發(fā)生在某一段風速區(qū)間內，據此判斷觀察到的振動為渦激振動，試驗(1)α=+5°位移時程和相應的頻譜圖,如圖5所示。

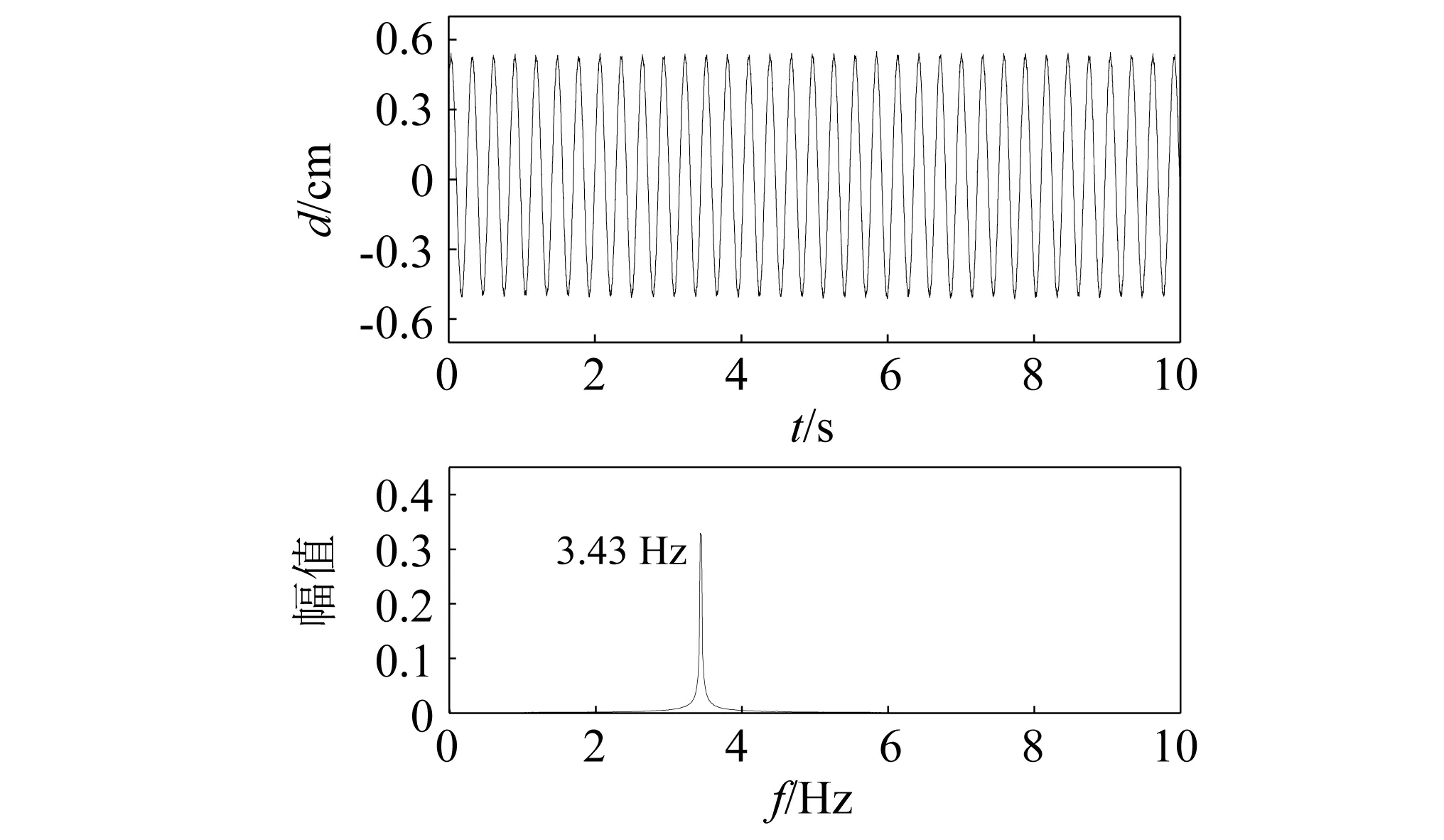
圖5 試驗(1)α=+5°位移時程曲線和頻譜圖Fig.5 Test (1)α=+5°displacement time-history curve and spectrum diagram

圖6為三組試驗分別在α=+5°和α=+3°時的振幅隨風速的變化情況，表1列出了三組試驗的具體振動結果。可以看出，風攻角對渦激振動存在顯著影響，風攻角越大，渦激振動越劇烈，α=+5°時模型的最大振幅大于α=+3°時的量值，且發(fā)生渦激振動的風速相對更低。這表明渦激振動對氣動外形十分敏感，當風攻角增大時，氣動外形發(fā)生變化，旋渦脫落強度更大，從而在更低的風速下激發(fā)出更顯著的渦激振動。另外，無論是α=+5°還是α=+3°，隨著雷諾數的增大，模型的最大振幅都呈逐漸減小的規(guī)律，表明雷諾數效應會導致振幅估計偏差。這與崔欣等[6]和張偉等[10]針對不同斷面形式的主梁雷諾數效應的研究結果基本一致。需要說明的是，由于通過調整模型系統的自振頻率來改變渦激振動的發(fā)生雷諾數，阻塞度、長寬比等都保持不變，三組試驗的唯一變量為雷諾數，因此，可以認為振幅的改變是雷諾數效應的結果。試驗是在連續(xù)幾天內完成，可認為三組試驗的溫度、濕度和壓強等相關參數沒有顯著的改變。

圖6 α=+5°和α=+3°三組試驗振幅隨風速變化曲線Fig.6 Amplitude changing with wind velocity at α=+5°, α=+3°

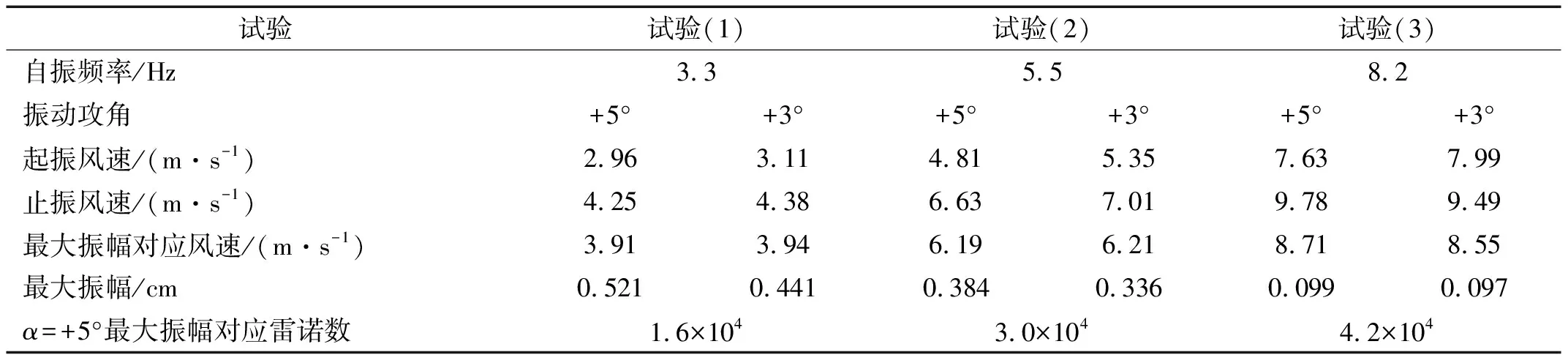
表1 三組試驗模型渦激振動結果

圖7為試驗(1)在α=+5°和α=+3°下，不同風速的旋渦脫落頻率。可以看出，非振動區(qū)間旋渦脫落頻率-風速曲線為一直線，計算的斯特羅哈數St≈0.19，據此預測的渦激振動起振風速約為1.2 m/s，但在該風速并未觀察到明顯的渦激振動。而發(fā)生明顯渦激振動的風速區(qū)間在3.2～4.4 m/s，且該鎖定不同于以往觀察到的直線型鎖定，而是在進入渦激振動風速區(qū)間后渦脫頻率突然下降至模型的自振頻率，表現為凹陷型鎖定。在國內外學者針對扁平流線型箱梁的渦激振動試驗中，多鎖定區(qū)間的渦激振動現象被多次發(fā)現[11-12]。

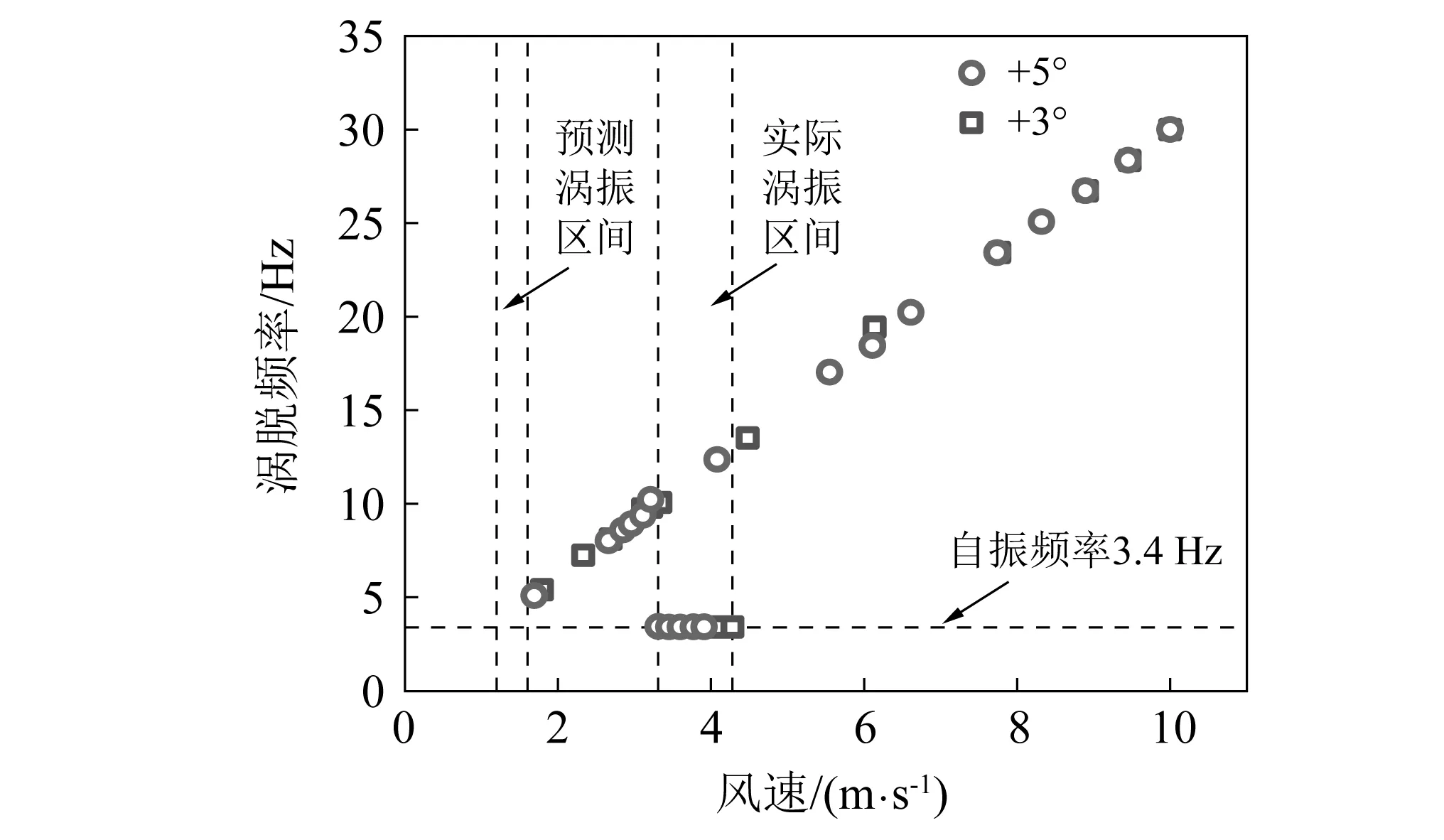
圖7 試驗(1)α=+5°和α=+3°渦脫頻率隨風速變化Fig.7 Variation in vortex shedding frequency with wind velocity at α=+5°, α=+3° for test (1)

根據文獻[13]，渦激振動出現多個鎖定區(qū)間可能是由不同頻率的旋渦脫落導致的，傳統的St數僅反映強度最大或尺寸最大的旋渦脫落，而脫落的漩渦中存在不同尺度的旋渦，導致氣動力也會含有豐富的頻率成分，當某一主要頻率與模型的自振頻率接近時，就可能激發(fā)渦激振動。圖8為試驗(1)在振動區(qū)間內某個風速下的升力系數時程及其頻譜圖，可以看出，升力系數的卓越頻率為3.4 Hz，正好與振動模型的自振頻率一致，因此激發(fā)了明顯的渦激振動。因此，判斷渦激振動是否發(fā)生和發(fā)生的風速范圍不能僅僅依賴St數來預測，宜通過風洞試驗、數值模擬等方法并結合相關實測數據進行確定。

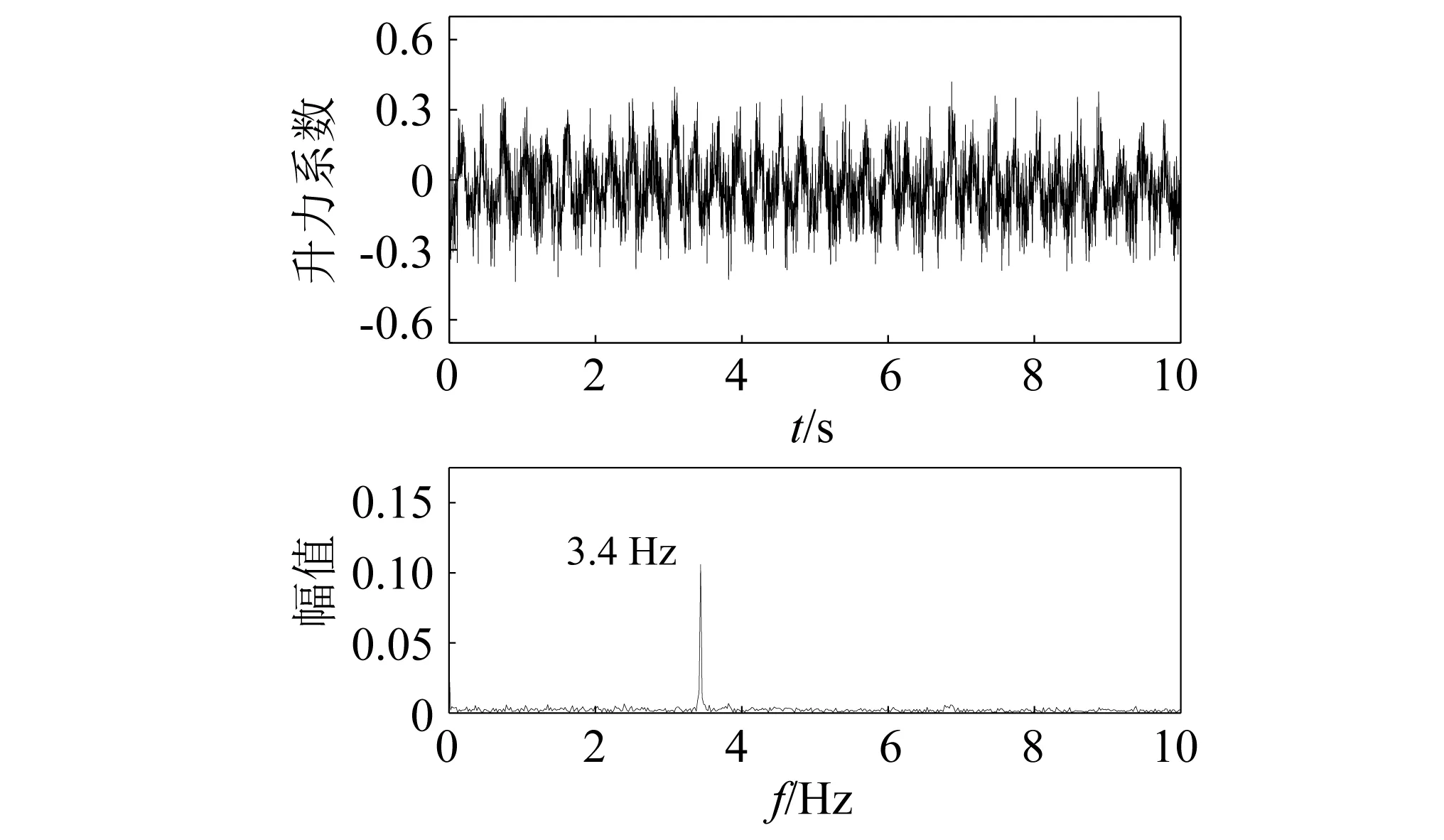
圖8 試驗(1) 振動區(qū)間內升力系數時程與頻譜Fig.8 Test (1) time history and frequency spectrum of lift coefficient in vibration range

2.2 主梁表面風壓分布規(guī)律

為了揭示渦激振動的深層機理，對模型表面的壓力分布規(guī)律進行研究，表面壓力可以通過風壓系數來表征，風壓系數定義如式(3)所示

(3)

式中：P為前方來流的靜壓；U為前方來流的速度；ρ為空氣密度；p(i)為測得的模型表面壓力信號的時間序列。測點的平均風壓系數為測點風壓系數時間序列的平均值，測點的脈動風壓系數為測點風壓系數時間序列的標準差。

根據表1可知，三組試驗中在α=+5°時，最大振幅對應的雷諾數分別為Re=1.6×104,Re=3.0×104和Re=4.2×104，為了研究雷諾數對風壓分布的影響規(guī)律，選擇這三個雷諾數下的風壓分布進行對比分析，平均風壓分布如圖9所示。

圖9 不同雷諾數下平均風壓分布Fig.9 Mean pressure distribution under various Reynolds numbers

首先，可以看出，主梁上下表面的平均風壓分布差異明顯，對于上表面而言，來流端風嘴附近處的平均風壓系數絕對值最大，沿著上斜腹板，平均風壓系數稍微減小，而在通過上斜腹板尖角時，平均風壓系數突然變化為負值，之后沿著上表面往下游方向，平均風壓系數沒有明顯變化，只在尾部欄桿扶手處出現較小波動。下表面的平均風壓分布曲線為典型的雙極值曲線，這是因為第一下斜腹板、腹板、第二下斜腹板的平均風壓分布呈現不同規(guī)律，在第一下斜腹板和腹板，腹板和第二下斜腹板交點位置處出現兩個極值點。在第一下斜腹板上，不同攻角下的規(guī)律也不同，后面會詳細分析；在腹板上，平均風壓系數的絕對值除了在兩端極值點處有所提高外，其他位置基本保持不變；在第二下斜腹板，平均風壓系數的絕對值沿著下游方向略微減小。

再者，對于上表面來說，風攻角僅改變平均風壓系數的數值，但并未改變平均風壓的整體分布規(guī)律。從α=-5°～+5°，隨著風攻角的增大，上斜腹板承受的風壓力逐漸減小，腹板承受的風吸力則越來越大。下表面的腹板和第二下斜腹板均主要承受風吸力，在負攻角時承受的吸力略大，受風攻角的影響相對較小。第一下斜腹板的平均風壓受風攻角的影響非常顯著，隨著無量綱距離的增大，平均風壓系數的絕對值先逐漸減小后逐漸增大，在α=+5°和α=+3°時，平均風系數最開始為正值，后逐漸變?yōu)樨撝担粚τ谄渌L攻角而言，平均風壓系數主要為負值，僅在α=0°時，風壓系數增大的過程中，存在幾個正值，表明氣流在尖嘴處就發(fā)生了分離，且風攻角越小，分離越明顯。

最后，對比不同雷諾數下的平均風壓分布規(guī)律，發(fā)現雷諾數的提高沒有對主梁上下表面在各風攻角下的平均風壓整體分布規(guī)律產生顯著影響，僅僅是數值發(fā)生了細微的改變，其中，雷諾數的改變對于下表面的平均風壓系數數值影響較上表面較大。

脈動風壓分布如圖10所示，主梁上下表面的脈動風壓分布也存在顯著不同，對于上表面，在不同的風攻角下，脈動風壓分布呈現不同規(guī)律，在α=+5°和α=+3°時，前緣和尾部的脈動風壓系數較大，α=+5°的脈動風壓系數較α=+3°時更大，而在其他風攻角下，脈動風壓系數較小且分布較為均勻。隨著雷諾數的增大，脈動風壓系數減小，在Re=4.2×104時，所有風攻角下的脈動風壓系數均非常小。

圖10 不同雷諾數下脈動風壓分布Fig.10 Fluctuant pressure distribution under various Reynolds numbers

對于下表面來說，除了α=+5°和α=+3°在Re=1.6×104下的前緣端和尾部端存在較大的脈動風壓系數，其余的風攻角和雷諾數工況下，脈動風壓系數均非常小。脈動風壓系數是由旋渦脫落引發(fā)的，其大小可以反映旋渦脫落的強度，進而解釋渦激振動。根據主梁上下表面的脈動風壓分布規(guī)律，可以認為上表面是決定渦激振動是否發(fā)生以及渦振響應強度的關鍵。并且，脈動風壓系數隨著雷諾數的增大而減小是導致渦激振幅減小的深層次原因。

2.3 測點氣動力相關性和渦激振動貢獻系數

模型部分測點存在較大的脈動風壓系數，可能對渦激振動的產生造成了影響。為了進一步探究模型表面不同區(qū)域對渦激振動的影響，針對三次試驗的氣動力相關性系數和渦激振動貢獻系數進行了分析。

模型表面測點的風壓與該測點代表面積的乘積可以表示測點代表區(qū)域所受到的氣動力，而整個箱梁斷面的氣動力可通過對所有測點的氣動力積分得到，兩者間的相關性用相關系數ρ來衡量，定義如式(4)所示

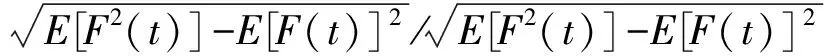
(4)

式中：f(t)為模型表面某一個測點所代表的面積受到的升力；F(t)為整個箱梁斷面受到的升力。仍然考察Re=1.6×104，Re=3.0×104和Re=4.2×104的相關情況，研究雷諾數對相關系數的影響規(guī)律。圖11為不同雷諾數下α=+5°的相關系數曲線。

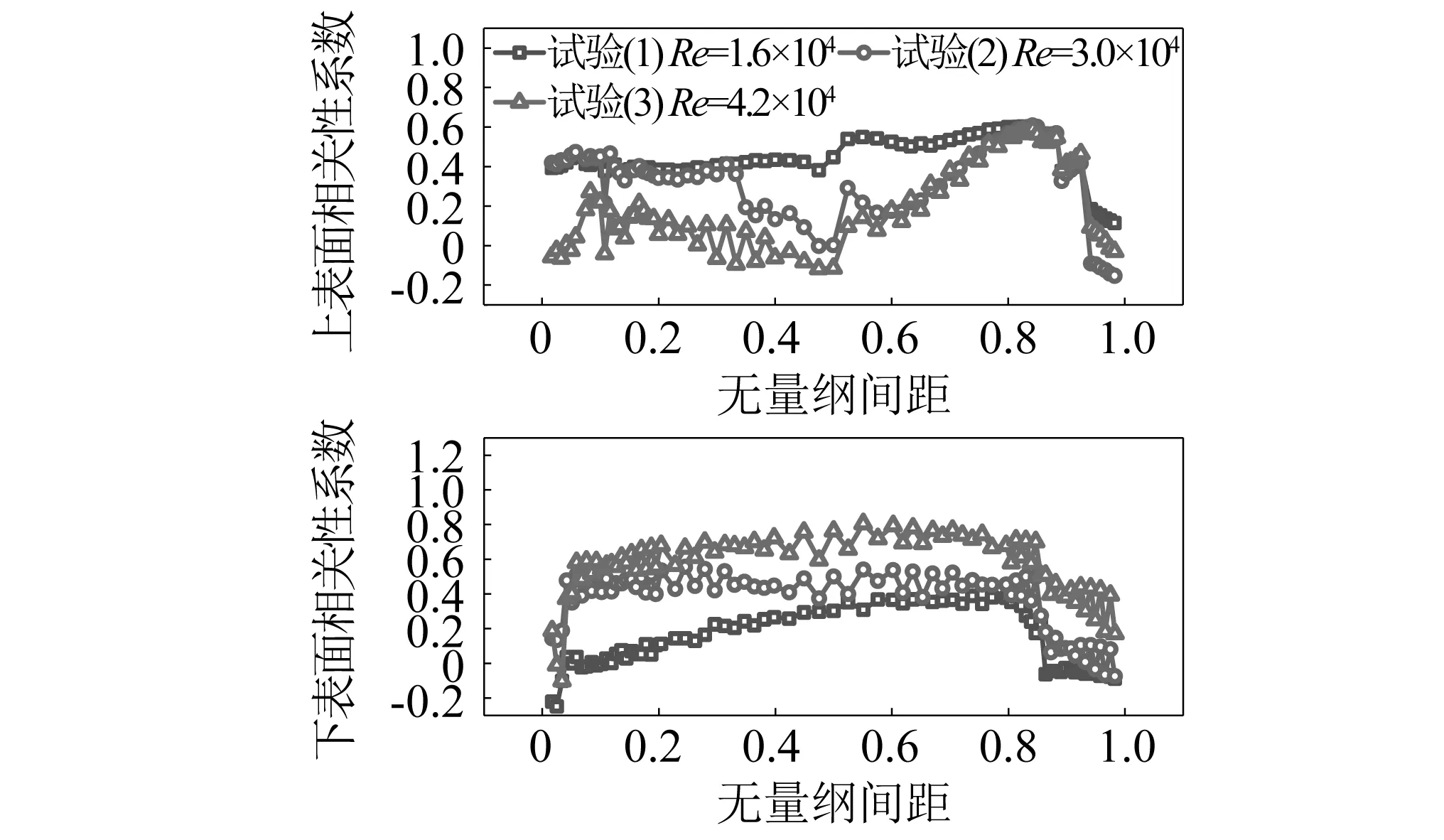
圖11 不同雷諾數下α=+5°模型氣動力相關性系數Fig.11 Aerodynamic correlation coefficient of α=+5° model at different reynolds numbers

可以看出，在Re=1.6×104時，上表面只有在Dd≥0.942的很小范圍內，相關系數在0附近，其余測點的相關系數均在0.4附近，且波動較小。在Re=3.0×104時，上表面Dd=0.500附近測點的相關系數下降至0值附近，其余部分與Re=1.6×104的相關系數相當。當雷諾數增大到Re=4.2×104時，前半部分的相關系數也明顯減小。下表面的相關系數基本呈現單峰式曲線，隨著雷諾數的增大，整體曲線呈現出上升趨勢Re=1.6×104時的相關系數最大值約為Re=4.2×104最大值的47%。可以看出，雷諾數會顯著影響主梁上下表面的相關系數，但是影響規(guī)律卻不同。隨著雷諾數的增大，上表面的相關系數逐漸減小，而下表面的相關系數逐漸增大。這表明由于雷諾數效應導致的主梁平均升力的變化，上、下表面對主梁的貢獻是相反的。

為了研究主梁表面測點對渦激振動的貢獻情況，特引入渦激振動貢獻系數CR，定義為測點脈動風壓系數和該測點相關系數的乘積，如式(5)所示

CR=Cp,rms·ρ[F(t),f(t)]

(5)

式中，Cp,rms為測點的脈動風壓系數。不同雷諾數下α=+5°的測點渦激振動貢獻系數曲線,如圖12所示。

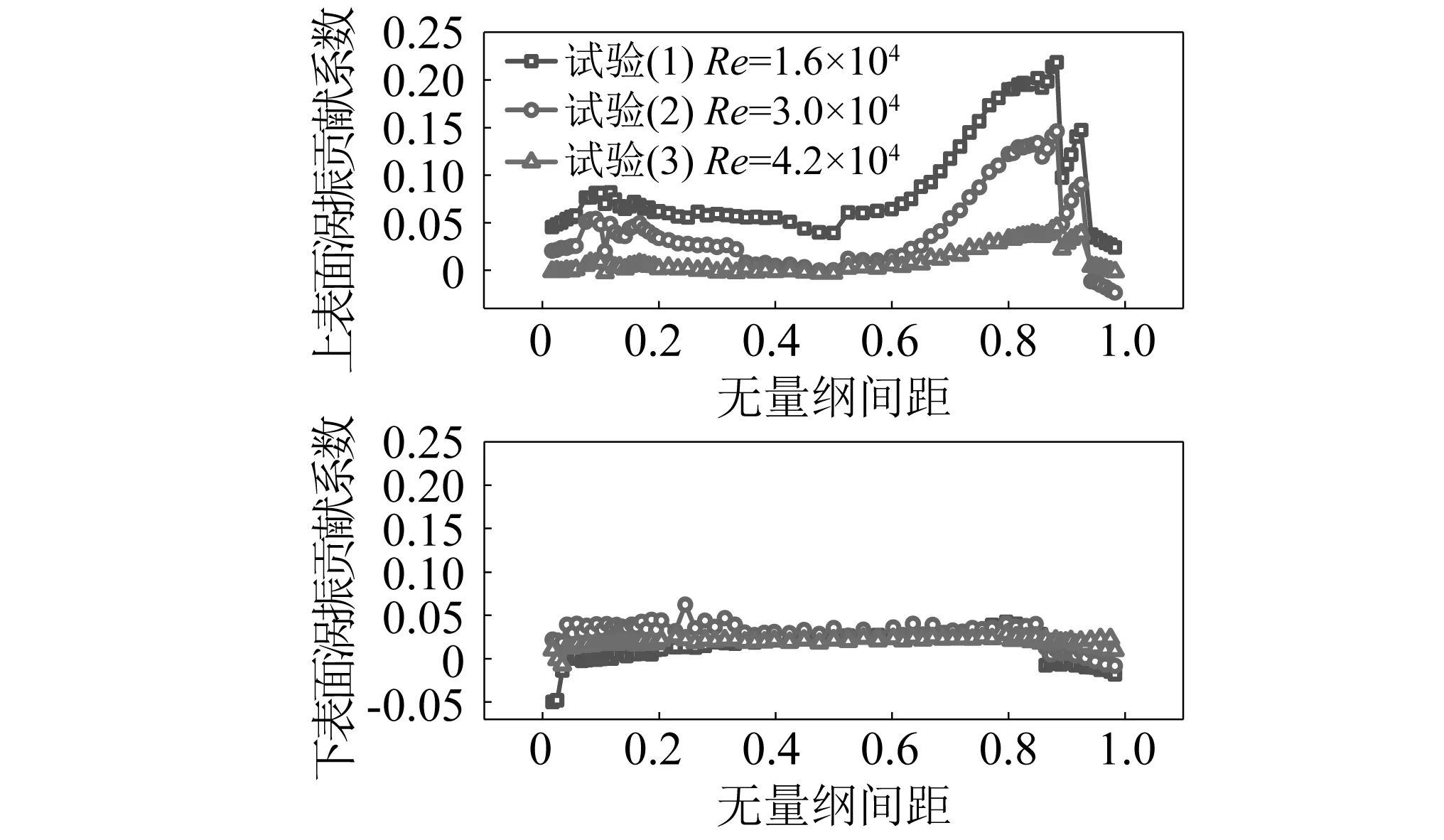
圖12 不同雷諾數下α=+5°模型渦激振動貢獻系數Fig.12 Contribution coefficient for vortex-induced vibration for α=+5° at various Reynolds numbers

根據圖12可得，在不同雷諾數下，渦激振動貢獻系數沿上表面的分布整體規(guī)律是接近的，即在無量綱間距Dd≤0.5時，渦激振動貢獻系數較小，但整體分布較均勻；當0.5≤Dd≤0.883時，隨著無量綱間距的增大，渦激振動貢獻系數逐漸增大；當0.883≤Dd時，渦激振動貢獻系數又開始減小。但是在不同的雷諾數下，在相同的無量綱位置，渦激振動貢獻系數的數值不同，且雷諾數越大，渦激振動貢獻系數越小，這和渦激振動振幅隨雷諾數增大而減小的規(guī)律是一致的。

下表面的渦激振動貢獻系數較小，數值在0附近，渦激振動貢獻系數沿下表面分布非常均勻，且隨雷諾數變化很小，表明下表面對渦激振動及渦激振動的雷諾數效應的貢獻均較小。

可以得出，針對研究涉及到的扁平流線型箱梁斷面，箱梁上表面下游區(qū)域對渦激振動的貢獻較大。脈動風壓系數和氣動力相關系數隨雷諾數的變化可能是導致渦激振動雷諾數效應的原因之一，其中，脈動風壓系數的變化造成的影響相對較大。

3 結 論

通過風洞同步測振和測壓試驗，對扁平流線型箱梁的渦激振動特性及雷諾數效應進行了研究，主要得出以下結論。

(1)扁平流線型箱梁的豎彎渦激振動存在明顯的雷諾數效應，低雷諾數下的渦激振動振幅要大于高雷諾數下的振幅，用低雷諾數下的結果來預測實橋的振幅偏于安全。

(2)由于旋渦脫落的復雜性，渦激振動可能出現在根據斯特羅哈數預測的風速區(qū)間之外，渦激振動測試建議通過風洞試驗、數值模擬等方法結合實測數據確定。

(3)箱梁上表面下游方向的半個區(qū)域對渦激振動的貢獻較大。模型的脈動風壓系數隨雷諾數的改變，可能是造成渦激振動雷諾數效應的原因。