2021 年高考平面向量問(wèn)題聚焦

■盧智軍

2021年高考對(duì)平面向量主要圍繞“向量平行或垂直的條件、向量的數(shù)量積運(yùn)算、向量的線性運(yùn)算、向量加減法的幾何意義以及最值”等問(wèn)題展開，凸顯向量“數(shù)與形”雙重身份求解問(wèn)題的數(shù)學(xué)素養(yǎng)。

聚焦1：向量平行與向量的線性運(yùn)算

聚焦2：向量的模的有關(guān)運(yùn)算

聚焦3：向量的數(shù)量積的幾何意義

例3（多選題）（2021年新高考全國(guó)卷）已知O為坐標(biāo)原點(diǎn)，點(diǎn)P1（cosα，sinα），P2（cosβ，－sinβ），P3（cos（α＋β），sin（α＋β）），A（1，0），則（ ）。

回味：本題涉及平面向量的數(shù)量積及坐標(biāo)運(yùn)算，又涉及三角恒等變換，是一道難度適中的好題。

聚焦4：向量的坐標(biāo)法的應(yīng)用

解：建立平面直角坐標(biāo)系xDy（如圖1），利用坐標(biāo)關(guān)系進(jìn)行判斷。

圖1

回味：借助數(shù)量積的坐標(biāo)運(yùn)算，探究軌跡方程，凸顯向量“數(shù)與形”的雙重身份。本題主要考查轉(zhuǎn)化能力和計(jì)算求解能力。

聚焦5：向量的數(shù)量積的最值問(wèn)題

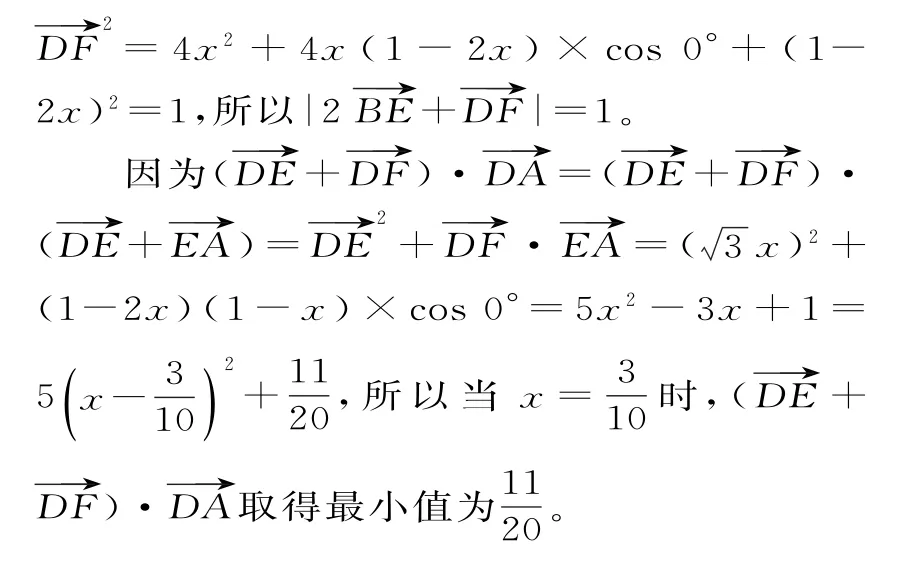
回味：通過(guò)向量的數(shù)量積運(yùn)算，將所求問(wèn)題轉(zhuǎn)化為解方程或解不等式或求函數(shù)值域，這是解決這類問(wèn)題的常用方法。

聚焦6：向量與不等式的交匯問(wèn)題

例6（2021年高考浙江卷）已知平面向量a，b，c（c≠0），滿足＝2，a·b＝0，（a－b）·c＝0。記向量d在a，b方向上的投影分別為x，y，d－a在c方向上的投影為z，則x2＋y2＋z2的最小值為____。

解：由題意可設(shè)a＝（1，0），b＝（0，2），c＝（m，n），則（a－b）·c＝m－2n＝0，即m＝2n。

回味：解答本題的關(guān)鍵是由平面向量的投影轉(zhuǎn)化為x，y，z之間的等量關(guān)系，再結(jié)合柯西不等式求得最小值。