基于人工魚群算法的加農炮內彈道參數優(yōu)化研究

何新佳，馬中亮，代淑蘭

(中北大學 環(huán)境與安全工程學院，山西 太原 030051)

火炮設計需要以內彈道計算為基礎，在內彈道計算中，火藥裝填條件或膛內構造諸元的改變都會使內彈道的計算結果大不相同[1]。裝填條件中只有裝藥量和火藥弧厚等少部分參數能得到較精確的值，而大多數參數值都是一個范圍，不易得到較精確的值，例如燃速系數和燃速指數等，其值大多通過密閉爆發(fā)器實驗得到。然而密閉爆發(fā)器和火炮膛內的實際情況不一樣，因此需要對燃速系數和燃速指數進行修正，以往大多靠經驗求得，缺乏一定的合理性。尤其是對于一些用來進行科學研究的新型發(fā)射藥，其配方復雜，加入的一些氧化劑等勢必會對發(fā)射藥的內部結構產生影響，導致燃速系數值和燃速指數值發(fā)生較大的改變，這時僅憑經驗修正費時費力，因此需要采用一些合理的優(yōu)化方法來對這些參數進行修正,以達到提高內彈道模型的精度和預示性的目的[2-3]。

近年來，各種優(yōu)化算法不斷涌現，如模擬退火算法、遺傳算法、粒子群算法等，這些方法具有良好的全局性、魯棒性強以及收斂速度較快的特點，均得到了廣泛地應用。相比上述算法，人工魚群算法對初值的要求不高，隨機產生或者固定為常數值均可，且全局尋優(yōu)能力強，能夠快速跳出局部最優(yōu)解，因此該算法在優(yōu)化設計方面得到了廣泛應用。冷杉等[4]將人工魚群算法結合粒子群算法應用到彈道優(yōu)化中，設計得出了導彈滑翔段的優(yōu)化彈道。李曉蘇等[5]將人工魚群算法應用到運載火箭上升段的彈道優(yōu)化設計中，結果表明了魚群算法能有效求解多級固體火箭上升段的彈道優(yōu)化問題。基于此，筆者以100 mm加農炮內彈道數學模型為算例，采用人工魚群算法對內彈道參數進行優(yōu)化。

1 內彈道數學模型

100 mm加農炮采用的發(fā)射藥是單一的管狀藥，因此不需要考慮發(fā)射藥的燃燒分裂點問題。在經過一系列簡化假設的基礎上，100 mm加農炮經典內彈道方程組可以寫為

(1)

式中：lψ=l0[1-Δ(1-ψ)/ρp-αΔψ]，l0為藥室容積縮徑長，l0=V0/S，V0為藥室容積；Δ=ω/V0；Ik為壓力全沖量，Ik=e1/u1；θ=k-1；Z為火藥燃去的相對厚度；p為加農炮膛內壓力；l為彈丸的行程；ω為發(fā)射藥裝藥量；m為彈丸質量；φ為次要功計算系數；α為火藥氣體余容；ρ為發(fā)射藥固體顆粒的密度；χ,λ,μ為火藥的形狀特征量；k為火藥氣體絕熱指數；f為火藥力；u1為發(fā)射藥的燃速系數；e1為管狀發(fā)射藥弧厚的一半；n為燃速指數；S為炮膛橫截面面積；lψ為藥室的自由容積縮徑長。

2 內彈道參數優(yōu)化過程描述

內彈道數學模型描述了系統的已知量和未知量的關系，用數學方程的形式給出了裝填條件和火炮構造諸元與內彈道性能的關系。對內彈道參數進行優(yōu)化時，需要在滿足內彈道性能指標的條件下，找到優(yōu)化目標函數的裝填條件和火炮構造諸元[1]。

2.1 確定設計變量

內彈道參數優(yōu)化時，對內彈道計算結果影響較大的有燃速系數、燃速指數、裝填密度、相對裝藥量和絕熱指數等。由于燃速系數和燃速指數相比火藥弧厚、相對裝藥量等其他參數更加難以得到較精確的值，因此以火藥的燃速系數u1和燃速指數n作為需要優(yōu)化的參數。

2.2 建立約束條件

約束條件是對內彈道參數優(yōu)化時參數取值的限制，或是對參數本身提出的限制條件。參考文獻[1]確定火藥燃速系數u1的取值范圍為：8.3×10-10m/(s·Pan)≤u1≤9.0×10-10m/(s·Pan)，燃速指數的取值范圍為：0.92≤n≤1.0。

2.3 選擇目標函數

目標函數是用來評價設計目標優(yōu)劣的數學關系式，目標函數應是設計變量的函數。由加農炮內彈道數學模型可知，內彈道參數(如裝藥量，火藥弧厚和燃速系數等)與內彈道計算結果(如膛壓和初速等)呈隱式非線性關系，如果改變內彈道參數，內彈道計算結果也會隨之改變。為了使內彈道計算結果與靶場試驗結果盡量一致，以最大膛壓、初速的計算值與靶場試驗值的平均相對誤差e為目標函數，其計算公式為

(2)

式中：p,vg為仿真值；psid,vg,sid為靶場試驗值。

2.4 建立適應度函數

為了評價每次迭代后變量的優(yōu)劣程度，且算法在接近收斂時，目標函數取值很小，繼續(xù)優(yōu)化的潛能降低，導致可能獲得某個局部最優(yōu)解，因此為了解決上述問題，需要建立適應度函數，其計算公式為

fFit=1/(1+e),

(3)

式中：fFit為適應度值；e為上述的平均相對誤差。

為了使結果得到更好的精度，且盡量減少程序運行時間，因此在算法進行過程中，當fFit取值為0.999～1時，該算法就被認為終止。

3 人工魚群算法

人工魚群算法是一種基于模擬魚群行為的優(yōu)化算法。在一片水域中，魚群生存數目最多的地方就是該水域營養(yǎng)物質最豐富的地方，根據這一特點來模仿人工魚群的覓食行為，進而實現全局尋優(yōu)，這就是人工魚群算法的基本思想[6-7]。

3.1 覓食行為

設人工魚當前狀態(tài)為Xi，人工魚Xi在視野內隨機選擇一個狀態(tài)Xj，分別計算人工魚適應度值并進行比較，如果發(fā)現Yj比Yi優(yōu)(Yj和Yi分別為Xj和Xi的適應度值),則Xi向Xj移動一步:

Xj=Xi+RrandVs,

(4)

否則，人工魚Xi繼續(xù)在其視野范圍內選擇下一個狀態(tài)Xnext:

(5)

反復嘗試Tr次后，若仍沒有滿足前進條件，則人工魚Xi隨機繼續(xù)向前移動一步:

Xnext=Xi+RrandSt,

(6)

式中：Rnext為0到1之間的隨機數；St為移動步長。

如圖1，假設一條虛擬人工魚當前位置為X,Vs為人工魚的視野范圍，位置Xv為人工魚Xi在某時刻的視點所在位置。若此時該位置食物濃度高于當前位置，則人工魚向前移動一步，到達Xnext，否則人工魚X繼續(xù)尋求視野內的其他位置，判斷是否滿足前進條件[8-12]。若嘗試Tr次后仍沒有找到滿足前進的條件，則按式(6)繼續(xù)執(zhí)行下一步。

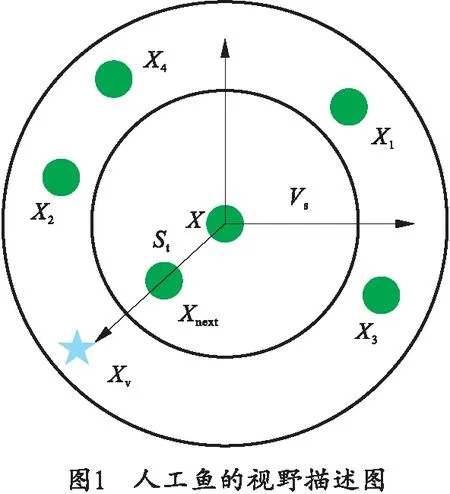
3.2 聚群行為

人工魚搜索視野范圍內的魚群數目nf及中心位置Xc，若Yc/nf<δYi,表明伙伴中心位置不太擁擠且該位置狀態(tài)較優(yōu)，則人工魚Xi朝伙伴中心位置移動一步，否則執(zhí)行覓食行為，其中δ為擁擠度因子。聚群行為可以促進陷于局部最優(yōu)解的人工魚群向全局最優(yōu)解的人工魚方向聚集，從而跳出局部最優(yōu)解。

3.3 追尾行為

人工魚Xi搜索其視野內適應度最高的個體Xj，其適應度值為Yj，并探索人工魚Xj視野范圍內伙伴數目nf,若Yj/nf<δYi，則表明Xj狀態(tài)較優(yōu)，且不太擁擠，Xi向Xj前進一步，否則執(zhí)行覓食行為。

3.4 隨機行為

隨機行為指人工魚Xi可以在其視野范圍內隨機移動，且會向食物較多的方向快速移動：

Xnext=Xi+VsRrand.

(7)

隨機行為可以讓人工魚個體更好地跳出局部最優(yōu)解。

3.5 加農炮內彈道參數優(yōu)化算法

人工魚群算法在運行過程中，人工魚會同時隨機的進行聚群行為和追尾行為，若發(fā)現聚群對象和追尾對象周圍擁擠度過大時，人工魚就會選擇覓食行為，若人工魚在覓食行為中沒有發(fā)現比自身適應度更高的個體，則按步長隨機移動一步，最后對聚群行為和追尾行為得到的適應度值進行比較[13-16]。為了使加農炮內彈道計算結果與測試結果的相對誤差盡可能小，因此在本文中選擇適應度值較大的人工魚作為下一代的個體。

利用魚群算法優(yōu)化加農炮內彈道參數時，當要計算人工魚個體適應度時，需調用內彈道方程組的求解程序，算出一系列約束條件范圍內的燃速系數u1的值和燃速指數n的值，再代入人工魚群算法的程序中計算出目標函數值，最后根據上述的轉換關系式得到適應度值。這里人工魚的個體代表需要優(yōu)化的加農炮內彈道參數值，即燃速系數u1和燃速指數n的值。加農炮內彈道參數優(yōu)化的流程圖如圖2所示，其中N為迭代次數，Nmax為最大迭代次數。

4 算例及結果分析

4.1 初始參數

選用以100 mm加農炮內彈道的設計參數為初始參數，火炮所用的發(fā)射藥為單一管狀藥。100 mm加農炮的初始參數如表1、2所示[1,17]。

表1 裝填條件參數

表2 計算條件參數

4.2 仿真計算

為了達到精度要求，且盡量加快算法的收斂速度，取人工魚個體數目N為100，算法迭代次數為50次，人工魚視野Vs為1，擁擠度因子δ為0.618，人工魚前進步長為0.5，人工魚嘗試次數Ntry為15次[18-20]，計算得到的目標函數值要求不大于0.001，此精度在工程實際中已滿足要求。在算法進行過程中，當連續(xù)多次所得的適應度值在0.999～1之間時，算法終止。仿真計算得到的適應度值隨迭代次數的變化關系圖如圖3所示。由圖中的變化曲線可知，當算法進行到第36次時，適應度值已在0.999～1之間，其值為0.999 09，該適應度對應的目標函數值的誤差已經小于0.001，完全滿足工程實際的要求。

為了更好地說明內彈道優(yōu)化參數的變化情況，得到的燃速系數和燃速指數隨迭代次數的曲線變化圖，分別如圖4、5所示。

從圖4、5中可以看出，在迭代進行到第36次時，達到了所要求的精度，且燃速系數和燃速指數隨迭代次數的變化情況與適應度值隨迭代次數的變化情況完全相符。此時對應的燃速系數和燃速指數的值分別為

u1=8.602 0×10-10m/(s·Pan),n=0.971 3。

此時仿真得到的最大膛壓值與初速值如表3所示。由表3可知，仿真得到的最大膛壓和初速的相對誤差均低于0.1%，與靶場射擊試驗結果符合得很好。

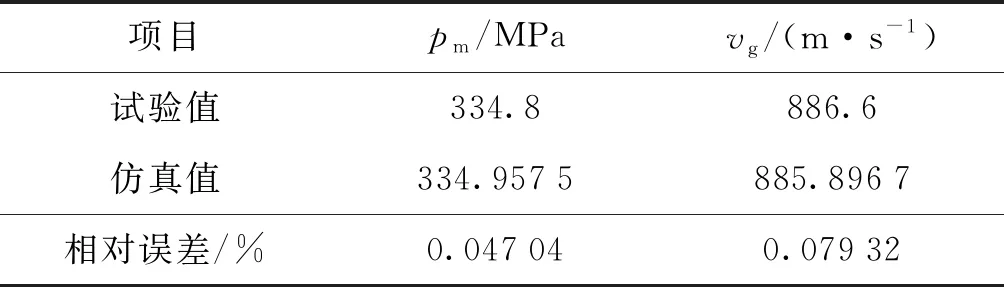
表3 最大膛壓值與初速值

為了驗證魚群算法的可行性及實用性，將優(yōu)化后的參數代入到加農炮內彈道數學模型，由于內彈道微分方程組只能運用數值計算的方法進行求解，因此選用四階龍格-庫塔法進行數值求解，并與參數優(yōu)化前計算得到的結果進行比較，其膛內壓力和彈丸速度隨時間的變化曲線如圖6、7所示。膛內壓力和彈丸速度隨彈丸行程的變化曲線如圖8、9所示。

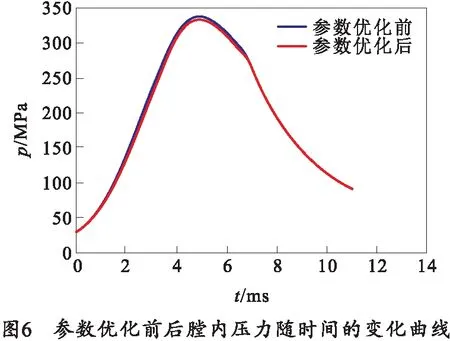
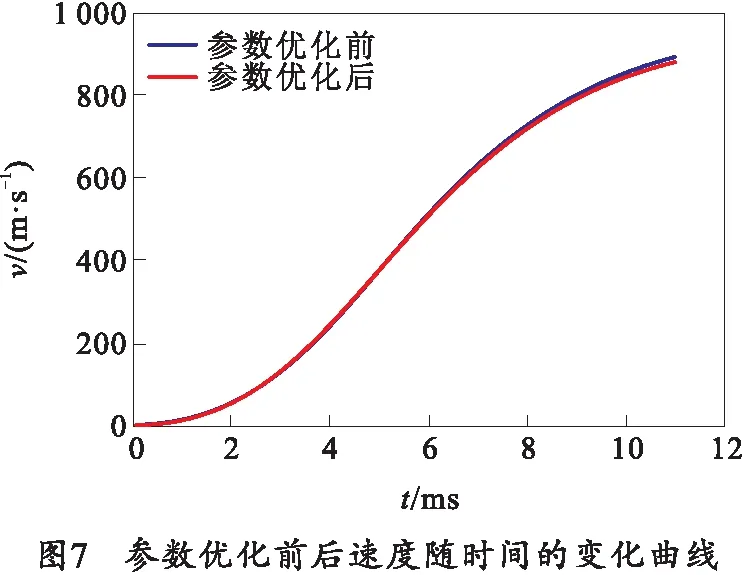
從圖6～9中可以看出膛內最大壓力值和炮口初速值在內彈道參數優(yōu)化前后都有明顯的變化，體現出燃速系數和燃速指數對內彈道性能影響較大的特點。

加農炮內彈道參數優(yōu)化前后得到的最大壓力與炮口初速如表4所示。從表中的參數優(yōu)化前后結果看，優(yōu)化后炮口初速的計算值與試驗值的相對誤差僅為0.017%，相比優(yōu)化前，已經具有很高的精度。優(yōu)化后的計算結果與靶場射擊試驗結果吻合得很好，該對比結果進一步證明人工魚群算法應用到加農炮內彈道參數優(yōu)化中的適用性。

表4 加農炮內彈道參數優(yōu)化結果

5 結束語

筆者采用加農炮經典內彈道數學模型，利用人工魚群算法對加農炮內彈道參數進行優(yōu)化研究，該算法在迭代次數為36次時就已經達到所需的精度，體現了人工魚群算法收斂速度較快的特點。計算得到的最大膛壓相對誤差以及初速相對誤差均小于0.1%,滿足工程實際要求。將優(yōu)化后的參數代入到加農炮內彈道數學模型中進行內彈道計算，其最大膛壓和初速的計算結果與靶場射擊試驗結果的相對誤差均不超過0.1%，吻合得很好，顯示了人工魚群算法在內彈道參數優(yōu)化中的可行性以及適用性。該算法對火炮的裝藥設計及改進火炮內彈道性能等具有重要指導意義。