基于頻域分析的空調溫度控制系統的研究及仿真

吳 杰，孫小康

（1.江蘇省美術館技術設備保障部，江蘇南京 210018；2.揚州高等職業技術學校，江蘇揚州 225003）

空調已普遍存在于人們的生產生活中，對改善室內的空氣質量起著重要的作用。空調能耗占建筑物總能耗的一半以上。我國是一個資源緊缺的國家，空調的節能可靠運行有著非常重要的意義。計算機系統應用于空調系統可以實現對空調設備進行監督、控制和調節，改善空調系統的調節品質，提高可靠性和穩定性。所以近些年來對空調溫度控制系統的研究已成為熱點問題，空調溫度受外界和內部環境溫度、新風系統、季節變化等擾動影響，使室內溫度變化波動較明顯。空調系統結構復雜，無論是水系統冷量輸配或風系統送風輸出，通過管道行程長，路徑復雜等原因，導致空調系統具有較強的時滯特性[1-2]。空調溫度系統的被控對象常被看成具有時滯的一階、二階系統。工程上常采用基于響應曲線法的PID 整定、基于臨界比例法的PID 整定等傳統PID 方法對時滯系統進行控制，能夠較好地控制，但是在超調量過大、調節時間過長、外部擾動過大時會對系統產生震蕩現象，傳統的PID 難以得到滿意的控制效果。Smith 預估控制器的提出，有效地解決了時滯的補償。針對控制系統的模型失配、外部擾動等原因導致控制效果不理想等問題，文中對Smith 控制器進行廣義等效[3]，等效后的被控對象不含時滯過程，對其選用PID 控制結構，對閉環系統的特征方程進行分析，按工程實際選用合適的調節時間，分析閉環極點，整定控制器的PID 參數。文中方法相對于傳統的PID 整定、Smith 預估控制、內模-PID 整定方法具有更快的調節時間，超調量小，對外部干擾具有較好的魯棒性。

1 Smith預估控制

1.1 預估控制理論

Smith 滯后補償的方法是在被控對象的支路增加一個補償器，使增加后的閉環傳遞函數的特征方程中不含有時滯環節，從而改善控制系統的性能及穩定性。實際上預估模型不是并聯在過程上，而是反向并聯在控制器上，對Smith 預估控制器進行等效[4]，如圖1 所示。

圖1 Smith預估的控制框圖

圖2 中，引入Smith 預估補償后閉環系統的傳遞函數為：

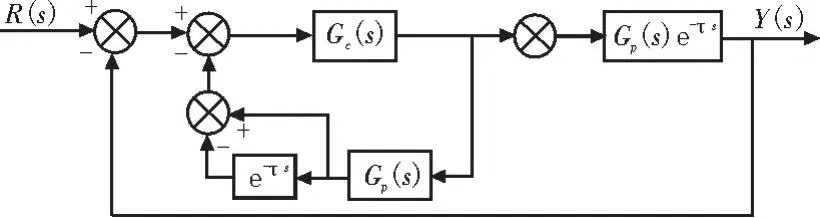
圖2 Smith預估控制的等效圖

式（1）中，Gc(s) 為控制器的傳遞函數，為被控制對象的傳遞函數，e-τs為被控對象的時滯環節。經過Smith 補償后，系統閉環特征方程中不含有時滯環節，閉環特征方程決定系統的穩定性，由于不含時滯環節，系統的穩定性得到很好的改善。下面對Smith 預估控制進行仿真分析，并研究其性能特點。

1.2 Smith 預估控制器仿真分析

某空調室內溫度控制對象一階時滯環節的數學模型為[5]：

式中，慣性環節T=144，延遲時間為30，增益系數為0.99，輸入信號為階躍信號。系統仿真如圖3所示。

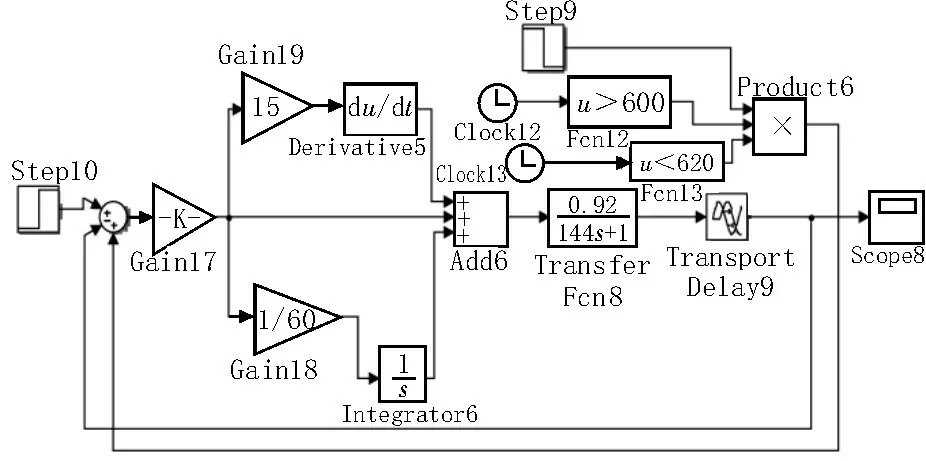
圖3 響應曲線法的PID整定在擾動下的仿真

圖3～5 的溫度控制參考值均為25 ℃，采用響應曲線法PID 控制、Smith-PID 預估控制對被控對象進行仿真[6-8]，其中對傳統PID 進行工程整定，各控制參數取Ki=0.1，Kp=6.1，Kd=91.5，Smith-PID 預估控制取Kp=10，Ki=0.5，Kd=200，并在穩定時刻加入一個20 s 的外部階躍擾動信號。從響應曲線可以看出，Smith-PID 預估控制在調節時間，超調量、擾動的恢復時間方面都比響應曲線的PID 控制優越，但同時Smith 預估控制仍有較大的超調量，且調節時間和擾動恢復時間較長、系統穩定性及魯棒性性能不高。

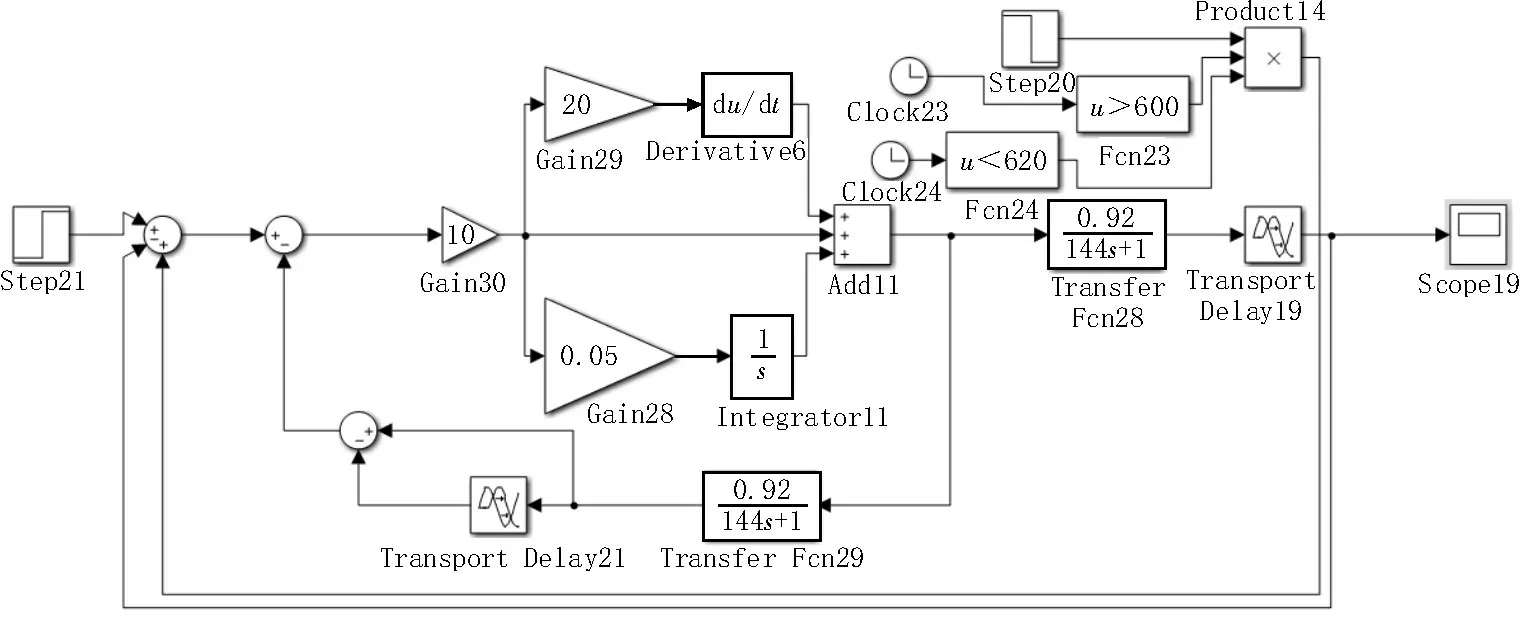
圖4 Smith-PID預估補償在擾動下的仿真

圖5 擾動下二種控制方法的響應曲線

2 頻域分析法的Smith控制器的改進

2.1 Smith 控制器等效分析

文中將預估控制器和被控對象廣義等效，將圖1的控制框圖等效如圖6 所示。

圖6 Smith預估器的廣義等效結構

其中，圖6 的系統結構圖可將虛線部分廣義等效為不含有時滯的被控對象Gp(s)，被控對象可以看成不含時滯的一二階系統，分別對不含有時滯的一二階系統選擇PID 控制結構，針對二階系統傳遞函數采用頻域法進行分析：

2.2 一階系統PID控制器參數整定

假設被控對象是一階系統模型[9]，傳遞函數為：

由式（4）可知，要使系統閉環傳遞函數化簡為二階系統的標準形式，擬采用PI控制器，用Gc()s表示為：

閉環系統的傳遞函數為：

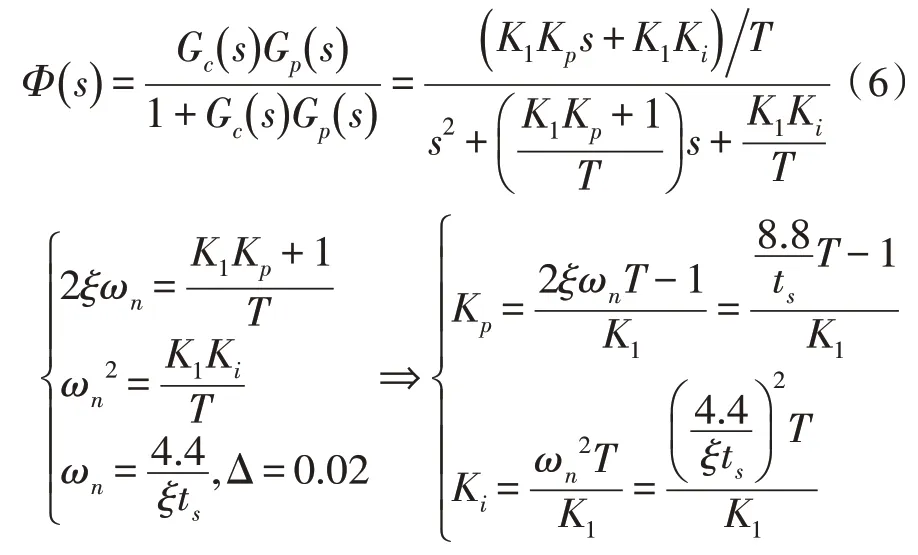
被控對象為一階系統的特征方程為：

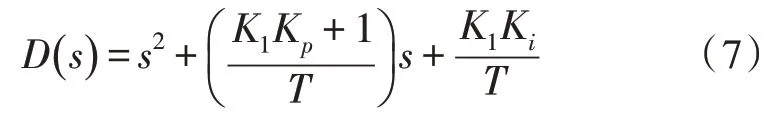
對于二階系統來說，在系統理想的情況下，系統工作在欠阻尼狀態，同時閉環系統的特征方程具有負實部的共軛復根。二階系統傳遞函數標準的特征方程形式為[10]：

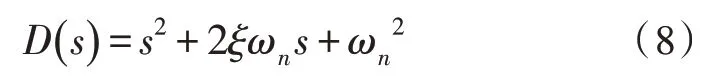
比較上式，可取：

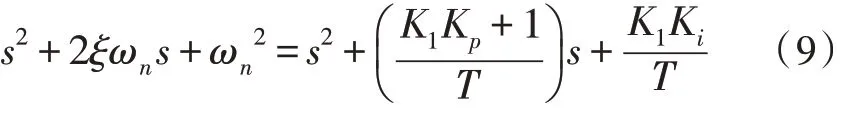
2.3 二階系統PID控制器參數整定

假設被控對象是二階系統模型[11]，傳遞函數為：

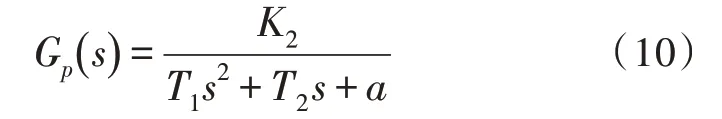
要使系統閉環傳遞函數化簡為二階系統的標準形式，擬采用PD 控制器，用Gc(s) 表示：

閉環系統的傳遞函數為：

參照式(7)～(10)的推導過程，被控對象為二階系統的特征方程需滿足：

根據工程實際情況選擇調節時間ts，在已知被控的一階、二階時滯的空調房間溫度的數學模型時，根據ξ、T1、T2、a、K1、K2等參數，分別計算一階、二階被控對象控制器的Kp、Ki、Kd值，通常取阻尼比ζ=0.4～0.8，文中取ζ=0.707。假設在某時刻加入擾動N(s)，根據圖6 的廣義等效法，系統的輸入輸出關系可表示為：

其中，

根據系統的穩態誤差和終值定理進行一般性推導如下：

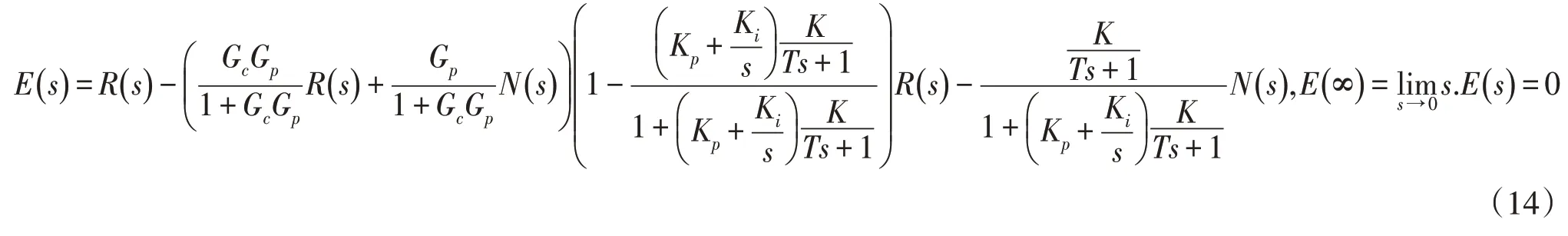
同理，二階系統E(∞)=0，可知一階、二階系統在時間趨于無窮時，系統穩態誤差均為0，因此系統具有較好的穩定性和跟蹤性能[12]。

3 實驗仿真

3.1 一階時滯空調溫度模型

文中選取某空調溫度模型的被控制對象為一階時滯環節，其數學模型為：

分別采用Smith-PID 預估控制、內模PID 控制和文中的控制方法分別進行實驗仿真。對于空調溫度的一階時滯系統，在某時刻加入20 s 的外界階躍擾動信號，內模PID 控制[13]采用FOPTD 的方法進行PI參數整定，其中Kp=2.45，Ki=0.017，文中方法采用PI控制器選取調節時間ts=5，ζ=0.707，T=144，K1=0.92，τ=30，計算得到Kp=274.39，Ki=242.49，仿真結果如圖7 所示。

圖7 外界擾動下的3種控制系統的階躍響應

3.2 二階時滯空調溫度模型

選取某空調溫度模型為二階時滯系統，根據有關空調房間與末端空調箱模型的文獻[14-15]、空調的溫度模型的二階時滯系統，空調房間溫度控制的傳遞函數G0(s)與末端空調箱的傳遞函數相乘可得：

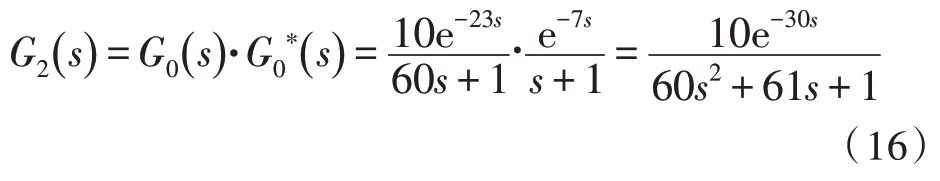
選取和一階時滯相同的方法進行仿真，內模PID控制采用SOPTD 的方法[16]進行PI 參數整定，其中Kp=0.1，Ki=0.387，Kd=0.001 6，文中方法選取調節時間ts=5 s，ζ=0.707，T1=60，T2=61，K2=10，τ=30，計算得到Kp=9.19，Kd=4.46，仿真結果如圖8 所示。

圖8 外界擾動下3種控制系統的階躍響應

根據圖7、圖8、表1、表2 的實驗仿真結果可知，文中方法的超調量比Smith-PID 預估控制明顯減少，且在系統調節時間、過程中擾動恢復時間方面的指標遠小于Smith-PID 預估控制和內模PID 控制，同時文中系統具有較好的跟蹤性能和魯棒性。

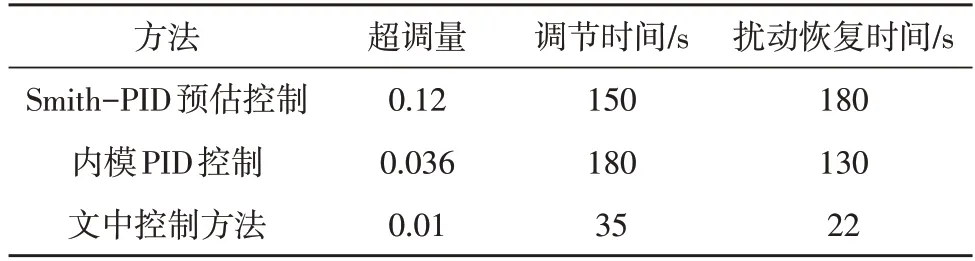
表1 系統性能指標

表2 系統性能指標

4 結論

文中提出了基于頻域分析的空調溫度控制方法，將Smith 預估器進行廣義等效成不含時滯系統，根據二階頻域的標準特征方程進行極點優化配置，選取不同的PID 結構對一、二階時滯進行控制，有效解決了空調溫度控制的時滯問題。仿真結果表明，該方法具有超調量較小、調節時間和擾動恢復時間短的特點，同時具有快速跟蹤擾動性能，可以為工程整定提供一定的參考。