黏彈性人工邊界在地下結(jié)構(gòu)抗震分析中的應(yīng)用

遲 恒，王壽生，王 維

[上海市政工程設(shè)計(jì)研究總院（集團(tuán)）有限公司，上海市 200092]

0 引言

城市地下結(jié)構(gòu),尤其是隧道、地鐵、地下車站、地下管線系統(tǒng),是現(xiàn)代社會(huì)公共基礎(chǔ)設(shè)施的重要組成部分。考慮到城市地下結(jié)構(gòu)對(duì)經(jīng)濟(jì)及生命安全的重要性,對(duì)地下結(jié)構(gòu)進(jìn)行抗震安全設(shè)計(jì)是必要的。依據(jù)《地下結(jié)構(gòu)抗震設(shè)計(jì)標(biāo)準(zhǔn)》（GB/T51336—2018）要求，對(duì)于地質(zhì)條件復(fù)雜（如：含軟弱、液化土層）且結(jié)構(gòu)體型復(fù)雜的地下結(jié)構(gòu)應(yīng)進(jìn)行彈塑性時(shí)程分析進(jìn)行抗震安全評(píng)估。而地震時(shí)地下結(jié)構(gòu)-土體相互作用是在無限域的場(chǎng)地中進(jìn)行，如何近真實(shí)地動(dòng)態(tài)模擬場(chǎng)地邊界成為分析結(jié)果可靠性的難點(diǎn)之一。圖1為廣義結(jié)構(gòu)與遠(yuǎn)場(chǎng)巖土之間設(shè)置虛擬人工邊界的整體計(jì)算模型[1]。

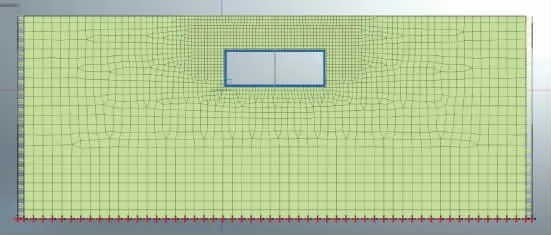
圖1 結(jié)構(gòu)-場(chǎng)地動(dòng)力計(jì)算模型

在無限連續(xù)土層介質(zhì)中采用虛擬邊界進(jìn)行有限化模擬，即構(gòu)建人工邊界。在無限域的場(chǎng)地模擬人工邊界不僅需滿足邊界設(shè)置要求條件,且可真正模擬無限域場(chǎng)地動(dòng)力特性。其土的力學(xué)分析上人工邊界為近場(chǎng)波動(dòng)對(duì)應(yīng)的偏微分方程。人工邊界條件的真實(shí)性為是否能準(zhǔn)確模擬對(duì)無限域連續(xù)介質(zhì)場(chǎng)地,即地震波在人工邊界處的傳播特性與無限域連續(xù)介質(zhì)保持統(tǒng)一。從近場(chǎng)任何方向入射的地震波通過設(shè)置的黏彈性人工邊界時(shí)無反射效應(yīng),即波在人工邊界處被邊界完全吸收，或完全透射。通常人工邊界也被認(rèn)為是無反射、透射或吸收的有限域邊界[2]。在地下結(jié)構(gòu)抗震分析中，人工邊界條件對(duì)無限域模擬的準(zhǔn)確與否將直接影響近場(chǎng)波動(dòng)數(shù)值模擬的精度,因此人工邊界條件的研究具有重要意義[3]。圖2為ANSYS場(chǎng)地分析模型。

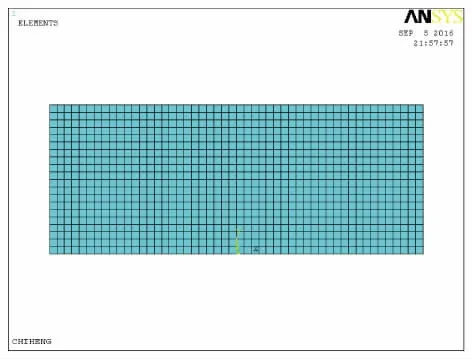
圖2 ANSYS場(chǎng)地分析模型

1 黏彈性人工邊界基本理論

Deeks等人提出假定二維散射波以柱面形式向外發(fā)散，模擬了黏彈性人工邊界。此后黏彈性人工邊界模型受到了國(guó)內(nèi)外眾多學(xué)者的關(guān)注，其中劉晶波等人做了大量的研究工作，例如，基于柱面波動(dòng)方程建立了二維黏彈性人工邊界[4]；并以球面波動(dòng)方程為基礎(chǔ)提出了三維黏黏彈性人工邊界[9]；依據(jù)半無限空間中的靜力問題基本解構(gòu)造出黏彈性靜動(dòng)力統(tǒng)一人工邊界以及方便工程應(yīng)用的二維、三維一致黏彈性人工邊界與等效黏彈性邊界單元，并就人工邊界的波源問題和地震波動(dòng)輸入問題進(jìn)行了系統(tǒng)性的討論，從而實(shí)現(xiàn)對(duì)實(shí)際連續(xù)介質(zhì)應(yīng)力邊界條件的模擬[5]。

此外，L.Kellezi在黏彈性人工邊界的研究中引入了波動(dòng)入射角度概念，對(duì)各入射角度賦予不同邊界參數(shù)，取得了較好的效果。然而，人工邊界是針對(duì)某種固定形式的外行波設(shè)置的，在近場(chǎng)地基地形和地質(zhì)條件均較復(fù)雜下會(huì)產(chǎn)生各種的散射波形式，以致使邊界對(duì)外行波的吸收不充分而產(chǎn)生誤差，那么在復(fù)雜地基條件下此類邊界模型的計(jì)算結(jié)果是否在工程精度要求將成為一個(gè)有待研究的課題。

1.1 黏彈性邊界的一般表達(dá)式

黏彈性人工邊界可表達(dá)為連續(xù)分布且相互偶聯(lián)的耗能彈簧-阻尼器，擬設(shè)人工邊界上法向及切向彈簧剛度和阻尼系數(shù)可按下列公式取值[6]：

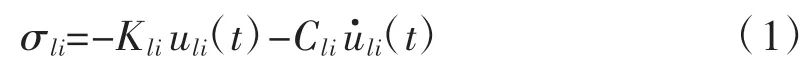
式中：l為人工邊界節(jié)點(diǎn)號(hào)；i=x，y，z代表分量方向；t表示時(shí)間；σli，uli，為節(jié)點(diǎn)方向的應(yīng)力、位移和速度；Kli，Cli為節(jié)點(diǎn)方向的黏彈邊界參數(shù)。

1.2 邊界節(jié)點(diǎn)運(yùn)動(dòng)方程

為真實(shí)模擬有限域邊界，考慮無限域動(dòng)力特性的黏彈性有限邊界表達(dá)時(shí)，邊界節(jié)點(diǎn)動(dòng)力方程可表達(dá)為：

式中：σli為黏彈性邊界處節(jié)點(diǎn)l應(yīng)力為節(jié)點(diǎn)l應(yīng)力的作用范圍；N為與節(jié)點(diǎn)震動(dòng)關(guān)聯(lián)的單元數(shù)；Ale為單元e上黏彈邊界的作用范圍，其中平面應(yīng)力分析，Ale則取值為1/2單元邊界線長(zhǎng)度[7]。

1.3 黏彈性邊界單元參數(shù)

將黏彈性人工邊界等效模擬成為連續(xù)分布的并偶聯(lián)的彈簧-阻尼器系統(tǒng)，如圖3所示。其中，平面分析中黏彈性人工邊界等效的彈簧特性為KB和阻尼系數(shù)CB分別為：

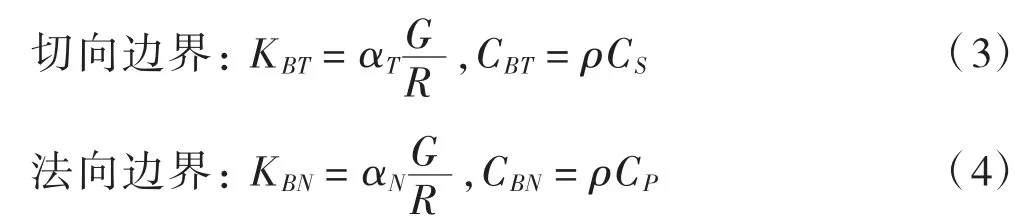
式中：KBT、KBN分別為法向與切向彈簧剛度；R為波源至人工邊界點(diǎn)的距離；CBT、CBN分別為垂直向與剪切向阻尼器的阻尼系數(shù)；CP、CS分別為介質(zhì)的P波和S波波速；G為介質(zhì)剪切模量；αN和αT分別為平面垂直向及剪切向黏彈性邊界修正系數(shù)；αT值范圍為[0.35，0.65]，αN的取值范圍為[0.80，1.20]，在本文中αN取為1.0，αT取為0.5。

1.4 黏彈邊界外源輸入方法

劉晶波和呂彥東給出一種將人工邊界入射場(chǎng)轉(zhuǎn)化為等效邊界力從而化外源波動(dòng)問題為內(nèi)源波動(dòng)問題的黏彈性人工邊界外源輸入方法，并在二維平面問題中得到應(yīng)用。由黏彈性邊界彈簧-阻尼元件和內(nèi)部計(jì)算區(qū)有限元模型共同構(gòu)成整體計(jì)算模型，當(dāng)人工邊界入射位移場(chǎng)在模型的人工邊界入射時(shí)，可以通過施加一個(gè)等效外荷載來代替人工邊界入射位移場(chǎng)。在邊界節(jié)點(diǎn)垂直向和剪切向上土體震動(dòng)位移所需施加的等效地震力可分為有限域介質(zhì)抵抗力及邊界彈簧-阻尼元件的反力。工程中，地震源距離場(chǎng)地比較遠(yuǎn)，一般把地震波假設(shè)為地表豎直自由向上入射的平面體波，例如垂直向上的平面SV波。入射場(chǎng)就是人工邊界入射場(chǎng)，側(cè)邊界無入射。質(zhì)點(diǎn)只有水平方向上的運(yùn)動(dòng)[8-10]。

2 數(shù)值分析

場(chǎng)地簡(jiǎn)化計(jì)算模型見圖3，并設(shè)4個(gè)觀測(cè)點(diǎn)。在模型底部垂直入射SV波，入射波位移方程式（5）和式（6）。通過提取左邊界上表面節(jié)點(diǎn)A和下表面的節(jié)點(diǎn)B的X向位移信息以及中間處上表面節(jié)點(diǎn)D和下表面的節(jié)點(diǎn)C的X向位移的對(duì)比情況，來驗(yàn)證黏彈性邊界的合理性（見圖4~圖5）。

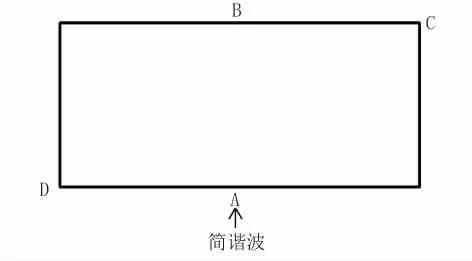
圖3 場(chǎng)地簡(jiǎn)化分析模型

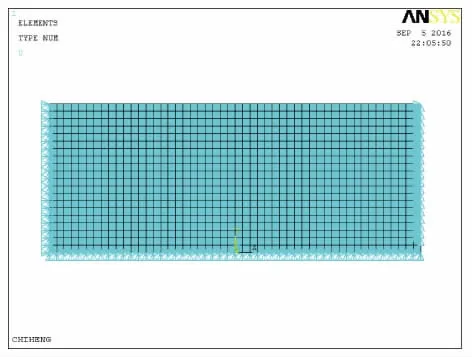
圖4 施加邊界約束

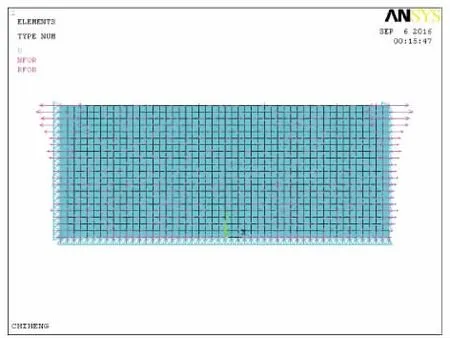
圖5 加載求解后的位移圖

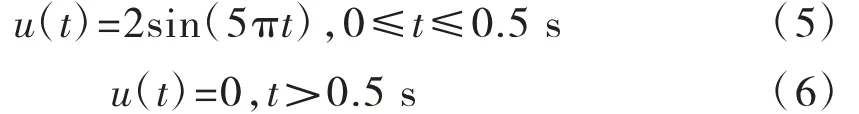
式中：u（t）為正弦位移加載函數(shù)，加載時(shí)間參數(shù)t≥0。介質(zhì)的彈性模量E=1.85×1010Pa，介質(zhì)的泊松比μ=0.35，介質(zhì)密度E=2637kg/m3。計(jì)算區(qū)域尺寸為：長(zhǎng)×寬=1000×400m。

模型中觀測(cè)點(diǎn)坐標(biāo)分別為A（0，0）,B（0，400），C（500，400），D（-500，0）。輸出D點(diǎn)位移、速度、加速度時(shí)程曲線圖，如圖6、圖7；A、B、C、D點(diǎn)位移時(shí)程曲線及各點(diǎn)間的對(duì)比曲線，如圖8~圖13。

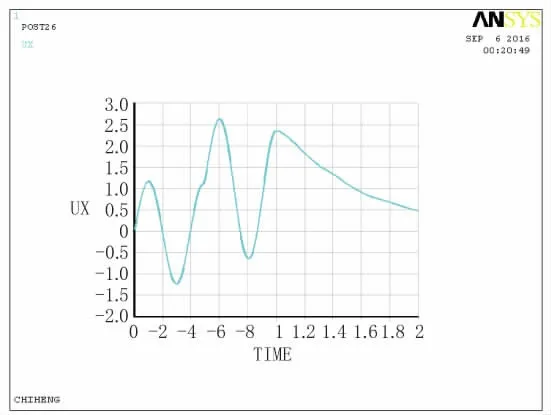
圖6 D點(diǎn)位移時(shí)程曲線圖

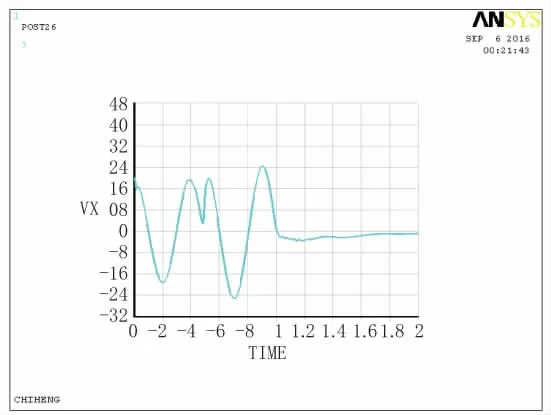
圖7 D點(diǎn)速度時(shí)程曲線圖

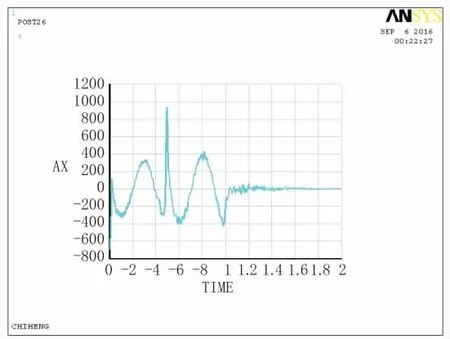
圖8 D點(diǎn)加速度時(shí)程曲線圖

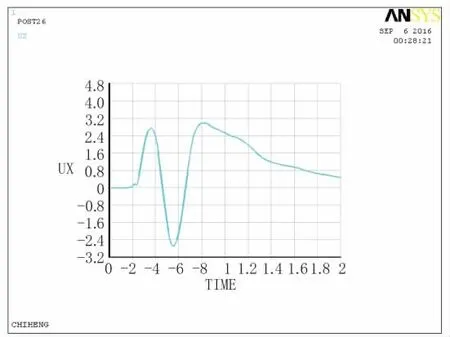
圖9 B點(diǎn)位移時(shí)程曲線圖

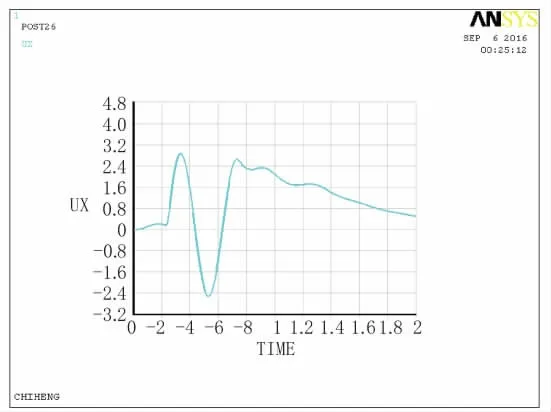
圖10 C點(diǎn)位移時(shí)程曲線圖

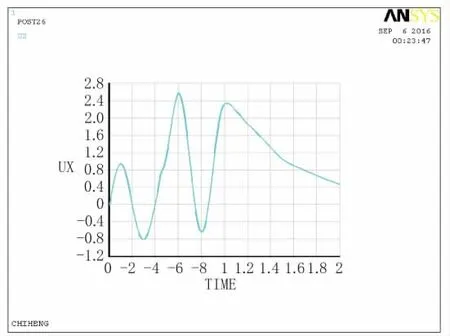
圖11 A點(diǎn)位移時(shí)程曲線圖

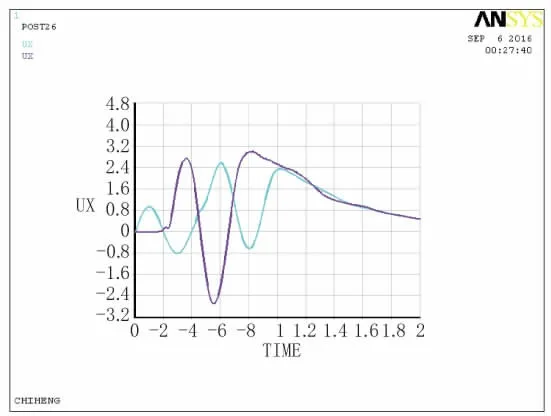
圖12 A點(diǎn)、B點(diǎn)位移時(shí)程曲線圖

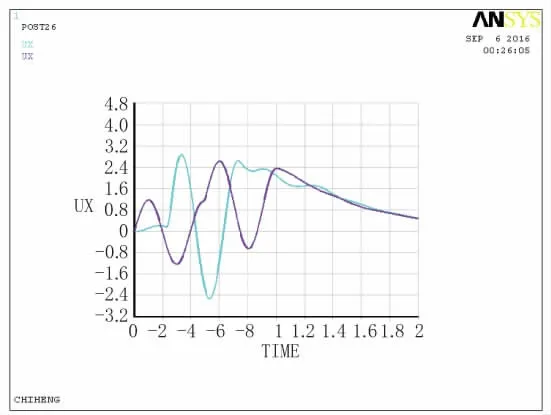
圖13 C點(diǎn)、D點(diǎn)位移時(shí)程曲線圖

通過對(duì)比各個(gè)觀測(cè)點(diǎn)的位移時(shí)程曲線及單點(diǎn)加速度、速度時(shí)程曲線可知，模擬邊界有效避免黏性邊界產(chǎn)生的低頻漂移現(xiàn)象，節(jié)點(diǎn)振動(dòng)和波的傳播速度及振幅想對(duì)應(yīng)，并且振動(dòng)能夠模擬場(chǎng)地有限區(qū)域之外的半無限介質(zhì)動(dòng)力恢復(fù)性能，說明土單元隨地震波動(dòng)具有穩(wěn)定的頻率。其中A點(diǎn)有一定的延時(shí)，為作用停止后的短暫時(shí)間內(nèi),會(huì)有滯后的位移,接著位移趨向?yàn)榱恪＿@都與理論解相一致。

其模擬邊界方法比其他常用邊界更易于在各種通用有限元程序中實(shí)現(xiàn)，因此，該邊界模型可較為真實(shí)的應(yīng)用于核電廠、地下綜合體結(jié)構(gòu)等重大工程的抗震安全分析及隔振工程數(shù)值分析。

3 ANSYS施加黏彈性邊界命令

4 結(jié) 語

本文對(duì)黏彈性人工邊界基本理論與等效荷載波動(dòng)輸入方法進(jìn)行了總結(jié)，并依據(jù)實(shí)際工程案例，實(shí)現(xiàn)ANSYS有限元自由場(chǎng)振動(dòng)分析與實(shí)際工程中的應(yīng)用。且通過計(jì)算表明黏彈性人工邊界具有滿意的計(jì)算精度和穩(wěn)定性，可廣泛應(yīng)用于地下工程抗震分析中。