剪切載荷作用下巖體結構面動態接觸特征數值模擬

蔣宇靜，張孫豪，欒恒杰，王長盛，王 冬，韓 偉

(1. 山東科技大學 能源與礦業工程學院，山東 青島 266590；2. 山東科技大學 礦山災害預防控制省部共建國家重點實驗室培育基地，山東 青島 266590；3. 長崎大學 工學研究科，日本 長崎 852-8521)

礦山、隧道、邊坡以及水利水電等各類工程巖體中存在大量的各種結構面，如斷層、節理、層理和裂隙等，破壞了巖體的整體性,導致巖體的強度和穩定性顯著降低。眾多工程實踐表明：結構面的剪切變形和滑移會導致工程失穩問題，嚴重威脅著人們的生命和財產安全。例如，當受到地下采礦和建筑活動干擾時，斷層容易發生滑動，從而對井下采掘空間甚至礦井地表造成嚴重損害，采礦誘發的斷層滑動引起的破壞性地震或巖爆正在成為世界范圍內深部開采安全的主要威脅。因此，深入研究巖體結構面的剪切特性對于工程災害防控具有重要意義。

自19世紀60年代以來，已有頗多關于巖體結構面剪切特性的研究成果，主要包括剪切強度、表面破壞特征、結構面抗剪強度與結構面表面形貌之間的關系以及巖石類型、邊界條件和加載方式等因素對它們的影響規律。巖體結構面剪切特性與表面形貌之間的關系更是巖石力學界在過去幾十年中研究的熱點問題。諸多學者提出了不同的JRC表征方法來描述結構面的表面形貌，并建立其與結構面剪切特性的關系。但是，這些JRC表征方法多是靜態的，無法表達剪切過程中粗糙體的部分退化、互鎖和分離，這限制了靜態JRC表征方法的功效。實際上，巖體結構面的剪切特性與接觸面的分布密切相關，各類因素大都是通過影響結構面的表面接觸特征進而影響其剪切特性。在剪切過程中，結構面只有部分是接觸的，并且接觸部分也隨著表面的滑動和破壞不斷變化。從力學的觀點來看，結構面的JRC必須以此為基礎來表征，了解接觸區域在法向和剪切載荷下的行為是量化結構面“有效”JRC的關鍵。因此，剪切作用下巖體結構面三維表面動態接觸特征的研究對于結構面剪切行為的評價和預測是至關重要的。

鑒于以上認識，國內外學者采用理論分析、室內試驗和數值模擬等方法對巖體結構面三維表面接觸特征進行了研究。理論研究方面，ZHAO等在Barton準則的基礎上考慮了結構面接觸對節理抗剪強度的影響，引入了節理匹配系數對Barton 準則進行修正。GRASSELLI首先研究了結構面接觸面積比與表面形貌參數的關系，并將接觸面積比作為一個重要指標，建立了結構面表面形貌參數與剪力學特性關系。該方法受到廣泛的認可，許多學者在此基礎上繼續研究了接觸面積比對粗糙節理剪切特性的影響，并發展了諸多新的結構面剪切強度模型。但是，目前理論研究中對于剪切過程中結構面表面接觸特征的演化鮮有報道。

試驗研究方面，PARK等總結指出：一些學者通過在結構面處插入壓敏紙、可變形薄膜、低熔點金屬和環氧樹脂等材料獲取結構面的接觸特征，但插入材料會影響結構面的剪切特性，且當考慮剪切位移時，更難以得到合理的結果；也有一些學者通過分析熱電偶溫度分布、電流通過阻力和CT掃描來間接確定結構面的接觸特征，但解釋測量信號和將測量信號定量應用于實際接觸區域時引入了可能的誤差，以上試驗方法仍需完善。近年來，透明材料在巖石力學領域得到廣泛應用。JU等利用3D打印技術和對應力敏感的光聚合物制作了透明的粗糙斷層模型，并提出了一種光學表征方法，提取和量化粗糙斷層模型周圍全場主應力差和剪應力的連續分布和演化。劉燕強等利用三維掃描和3D打印技術制作透明的粗糙度節理試件，實現了剪切過程中結構面接觸分布的可視化。但是，如何定量、全面地分析接觸面積和接觸應力等特征仍需深入研究。

數值模擬具有可視化的優點，可以實時定量地反映出結構面接觸情況。但考慮到計算效率，以往學者的研究主要集中于二維或規則的三維結構面，無法很好地還原結構面的真實剪切行為。針對三維粗糙結構面，FATHI等和XIAO等分別提出一種新的數值模擬方法來描述剪切過程中粗糙結構面接觸面積的變化，但卻難以表達接觸應力。進一步的，NGUYEN等和DANG等利用FLAC進行了粗糙結構面的直剪模擬，不僅直觀展現了剪切過程中的接觸面積的變化，還反映出剪切過程中的接觸應力狀態。但是，由于軟件自帶INRTERFACE本構模型并未考慮結構面粗糙度的退化，因此該方法僅適用于研究結構面粗糙度未退化或僅有少量破壞的情況。

綜上可見，雖然目前的研究成果可以一定程度上捕捉到巖體結構面三維表面的動態接觸特征，但尚無法滿足結構面剪切特性的研究需求。鑒于此，筆者首先修正了FLAC軟件自帶的INTERFACE本構模型，使其能夠準確表達粗糙結構面在剪切過程中的力學行為；然后，研究了剪切過程中結構面接觸和受力的分布及其演化規律，以及法向應力和JRC對接觸特征的影響規律；最后，通過分析結構面表面形貌-接觸特征-剪切應力3者間的關系，揭示了結構面剪切應力演化機理。

1 結構面本構模型的修正

1.1 自帶INTERFACE模型的不足

FLAC中提供了INTERFACE來模擬節理、斷層或層面等可能發生滑動或分離的弱面。INTERFACE是以庫侖滑動或拉剪切結合為特征的分界面，其具有摩擦力、黏聚力、剪脹、法向和剪切剛度、拉伸和剪切黏結強度等特性。INTERFACE的剪切行為由摩擦力、黏聚力和剪切剛度等決定。INTERFACE單元無法承受拉力，如其所受法向力為拉力或0，則剪力也為0，這是符合實際的。INTERFACE中采用線性庫侖抗剪強度準則作為界面滑動的判斷準則，其表達式為

=+tan

(1)

式中,為最大剪力；為黏聚力；為分界面節點相關聯的面積；為法向力；為摩擦角。

根據庫侖抗剪強度準則可知：當INTERFACE所受剪力超過設定的最大剪力后，界面將產生滑動。如圖1所示為通過室內試驗和數值模擬得到的法向應力2 MPa條件下的光滑結構面和粗糙結構面的剪切位移-剪切應力曲線，試驗和模擬方法詳見第3章。由圖1可看出，當結構面光滑時，采用自帶INTERFACE模擬得到的剪切位移-剪切應力曲線與室內試驗較為一致；而當結構面粗糙時，2者則有較大差異，模擬曲線在應力峰值后未出現明顯的應力跌落，應力降低速度緩慢。顯然，自帶INTERFACE尚無法準確模擬粗糙結構面的剪切行為。

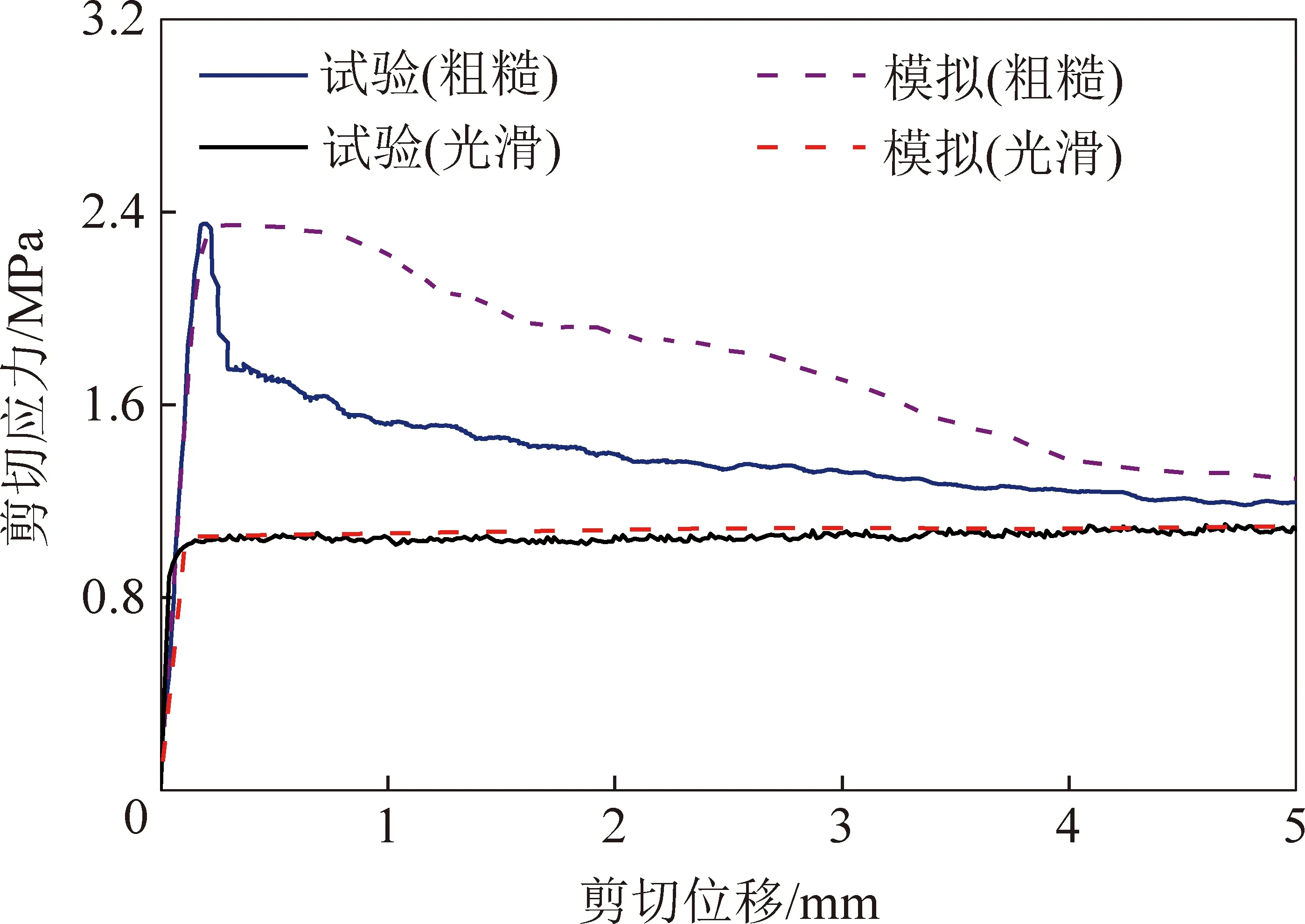
圖1 巖石結構面剪切位移-剪切應力曲線對比Fig.1 Comparison of shear displacement-shear stress curves of rock discontinuity

粗糙結構面在剪切過程中伴隨著結構面凸起的啃斷或摩擦破壞，而這種結構面的損傷行為在INTERFACE所采用的線性庫侖抗剪強度準則中未得到考慮，進而導致模擬結果與實際產生偏差，具體表現為結構面峰后剪切應力偏大。這正是由于通常情況下，結構面凸起的啃斷破壞發生在剪切應力峰值之后。因此，FLAC自帶INTERFACE僅能夠較好地模擬結構面的峰前剪切行為，但無法很好地模擬結構面的峰后剪切行為。然而，真實的巖體工程環境中，絕大多數結構面都具有一定的粗糙度，并且會在剪切滑移中產生顯著的損傷。此外，巖石結構面的峰后剪切行為對工程圍巖穩定性控制等也具有重要意義。鑒于以上認識，需對FLAC中自帶INTERFACE的本構模型進行修正，以期提高結構面剪切行為數值模擬的準確性。

1.2 模型修正

結構面的剪力由其黏聚力和摩擦力提供。以往學者研究表明：當巖石單元被判斷發生破壞后，應將其黏聚力降為0。這對于描述結構面剪切過程中的凸起破壞行為同樣是合理的。如圖2所示，當結構面凸起發生破壞后，破壞部分的黏聚力將不再發揮作用，結構面的抗剪力完全由摩擦力提供。因此，在數值模擬中當判斷得到INTERFACE單元破壞后，需將其黏聚力降為0，之后INTERFACE的剪力完全由摩擦力提供，計算公式為

=tan

(2)

式中,為結構面剪力。

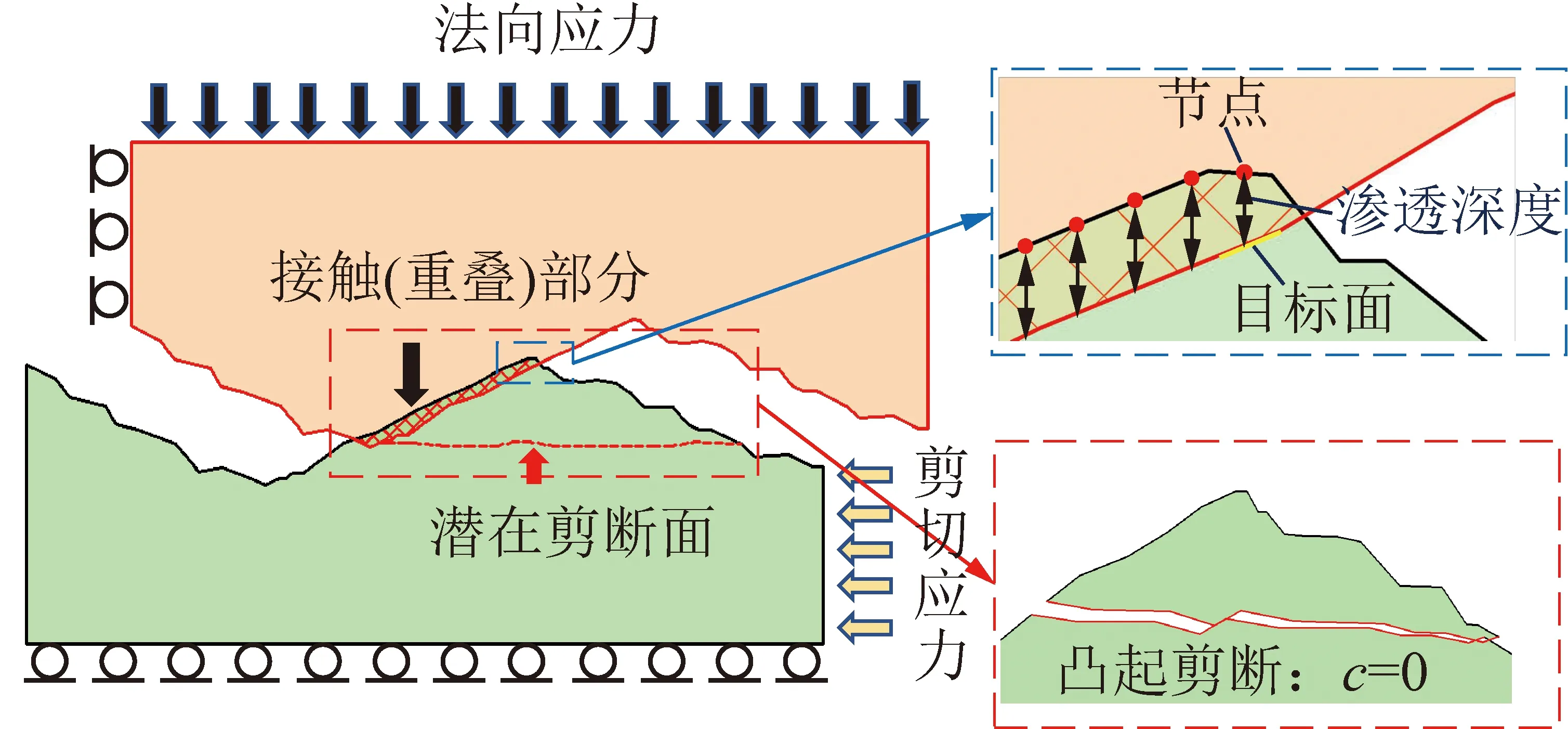
圖2 巖石結構面剪切破壞特征示意Fig.2 Schematic diagram of shear failure characteristic of rock discontinuity

由式(2)可知，結構面的剪力與其法向力呈正相關關系，INTERFACE中節點法向力的計算公式如下：

(3)

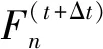
由式(3)可以看出，INTERFACE節點的法向力與節點滲透到目標面的絕對值深度相關。由圖2可見，自帶INTERFACE未考慮結構面凸起的破壞，導致凸起處節點的滲透深度偏大，進而造成法向應力偏大，甚至超過巖石的抗壓強度，如圖3所示。可以看出，結構面法向應力的最大值為74.12 MPa，遠高于選用材料的單軸抗壓強度38.29 MPa，與實際明顯不符。JING L等認為作用在結構上的法向應力上限應為巖石的單軸抗壓強度。這同時進一步說明了自帶INTERFACE無法很好地模擬粗糙結構面的剪切行為。

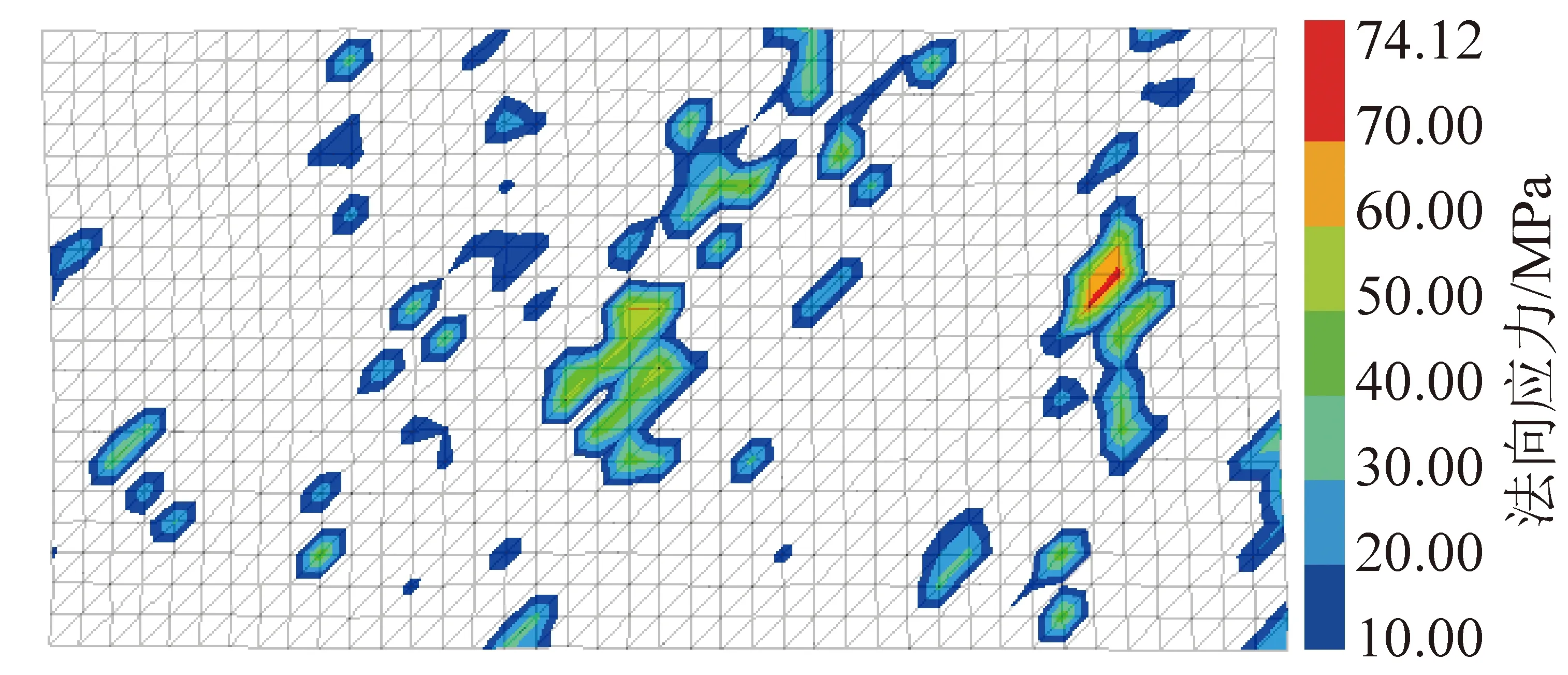
圖3 INTERFACE法向應力分布特征Fig.3 Normal stress distribution characteristic of INTERFACE

綜上所述，FLAC自帶INTERFACE無法很好地模擬結構面的峰后剪切行為，是由于結構面凸起未啃斷導致黏聚力和法向應力偏大。但是，由于FLAC采用的是有限差分方法，其無法實現單元體的破壞分離，此處即凸起啃斷。因此，筆者采用等效方法模擬結構面凸起的破壞，其具體修正流程如圖4所示(0為初始法向剛度；為時間步數)。首先建立模型并賦參，施加邊界條件之后開始進行剪切。每進行一步剪切時，首先需要判斷剪切位移是否到達目標值(10 mm)，當剪切位移還沒到達目標值時，開始遍歷INTERFACE單元進行破壞區域監測及變參，即從INTERFACE的第1個單元=1開始(共個單元)，通過摩爾庫侖強度準則對INTERFACE的破壞區域進行判斷識別，當被判別為破壞區域后對其力學參數進行修正，包括INTERFACE單元的黏聚力和法向剛度，然后進入到下一個INTERFACE單元即=+1單元，而當未被判別為破壞區域時則直接跳到下一個INTERFACE單元，直到遍歷整個INTERFACE的單元即>后退出破壞區域監測及變參部分。之后再進行下一步剪切，直到剪切位移達到目標值(10 mm)以后結束程序。通過以上修正方法，可使節點的剪力和法向力更接近實際情況，進而能夠更好地模擬出粗糙結構面剪切過程中抗剪強度的變化過程。

結構面凸起單元的破壞條件為INTERFACE剪力學行為修正中首要待解決的問題。在以往學者的研究中，通常將摩爾庫侖強度準則和最大拉應力準則作為巖石損傷的判斷準則，其表達式為

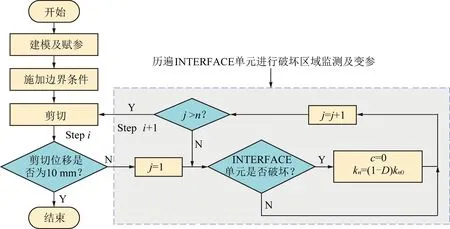
圖4 INTERFACE剪力學行為的修正流程Fig.4 Correction process for the shear mechanical behavior of INTERFACE

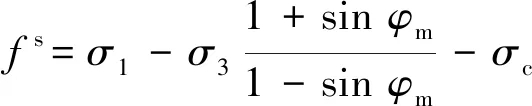
(4)

=-

(5)

式中,和分別為巖石的抗壓強度和抗拉強度；為剪切破壞判斷函數，當>0時單元體發生剪切破壞；為拉伸破壞判斷函數，當>0時則單元體發生拉伸破壞。

針對結構面破壞區域的法向受力問題，為了使模擬中INTERFACE破壞凸起單元的法向力更符合實際。借鑒相關文獻[44-45]中模擬巖石損傷的方法，通過賦予損傷因子來降低破壞單元的法向剛度，從而降低結構面法向應力，其計算公式為

=(1-)

(6)

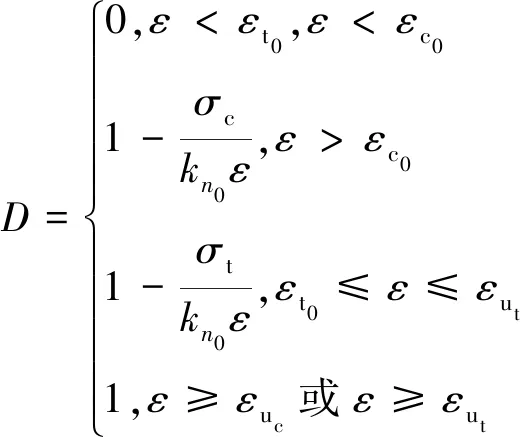
(7)

式中,為節點法向應變；c為抗壓峰值強度時的應變；t為抗拉峰值強度時的應變；u為極限抗拉應變；u為極限抗壓應變。

2 模型驗證

為驗證上述INTERFACE修正模型在模擬結構面剪切行為方面的準確性，開展室內試驗以進行對比驗證。

2.1 室內試驗方法

室內試驗結構面試件的尺寸為200 mm(長)×100 mm(寬)×100 mm(高)，采用類巖石材料制備，該材料質量配比為高強石膏∶水∶緩凝劑=1∶0.2∶0.005，其單軸抗壓強度和彈性模量分別為38.29 MPa和46.55 GPa。試驗中選取了表面形貌特征如圖5所示的3類具有不同粗糙度的結構面J1,J2和J3作為試件澆筑的模板，它們的粗糙度系數(JRC)分別為3.68,6.18和9.86。制作時首先使用復制花崗巖節理表面形態的硅橡膠模具澆筑上部試件，再以上部試件為模具澆筑下部試件，從而保證上部試件與下部試件吻合，試件澆筑完成后進行14 d的養護即可開展剪切試驗。加工完成的試件如圖6所示。

圖5 不同粗糙度巖石結構面的表面形貌Fig.5 Surface topographies of rock discontinuity with different joint roughness coefficients

圖6 制作完成的粗糙巖石結構面試件Fig.6 Completed rough rock discontinuity specimens

室內剪切試驗在如圖7所示的自主研發的MIS-233-1-55-03型法向應力伺服控制剪切試驗系統上開展，該剪切試驗系統的指標參數及試驗方法詳見文獻[47]。剪切試驗采用恒定法向應力邊界條件，考慮到常見錨固工程支護一般位于地下巷道、硐室等圍巖2～3 m以淺的范圍內，范圍內的圍巖應力遠低于原始地應力，根據相關經驗，選取法向應力分別為1,2,4 MPa。試驗時，首先以0.5 MPa/min的加載速度在剪切盒上方施加初始法向應力至給定值，然后以0.5 mm/min的速度在下部剪切盒上施加剪力至剪切位移達到10 mm。

2.2 數值模擬方法

為建立具有結構面表面真實形貌的數值模型，首先將利用三維激光掃描技術獲取的表面形貌數據轉化為ASCII格式，然后將其導入FLAC中，建立與室內試驗中試件尺寸一致的數值模型，如圖8所示。模型中共包含57 600個單元體和64 294個節點，單元體的平均尺寸為2.5 mm×2.5 mm×2.5 mm。在模型上下兩塊體間建立INTERFACE，模擬結構面剪切過程中的滑動力學行為。巖石塊體選用摩爾庫侖本構模型，相關參數通過試驗測得；結構面選用修正的INTERFACE模型，相關參數通過“試錯法”確定；巖石和結構面的物理力學參數見表1。數值模型的邊界條件與室內試驗相一致，即在模型頂面施加恒定法向應力，模型底面在法向方向上固定，上部塊體右側在剪切方向上固定。待對模型施加法向載荷并計算達到初始平衡后，通過給下部塊體施加與室內試驗相同的水平速度實現結構面的剪切。模擬過程中對結構面的受力變形特征等進行實時監測。以速度加載面上節點的水平位移代表結構面的剪切位移，以INTERFACE上的剪切應力代表結構面自身所受剪切應力，以INTERFACE接觸代表結構面的接觸狀態。

圖7 剪切試驗系統Fig.7 Shear testing apparatus

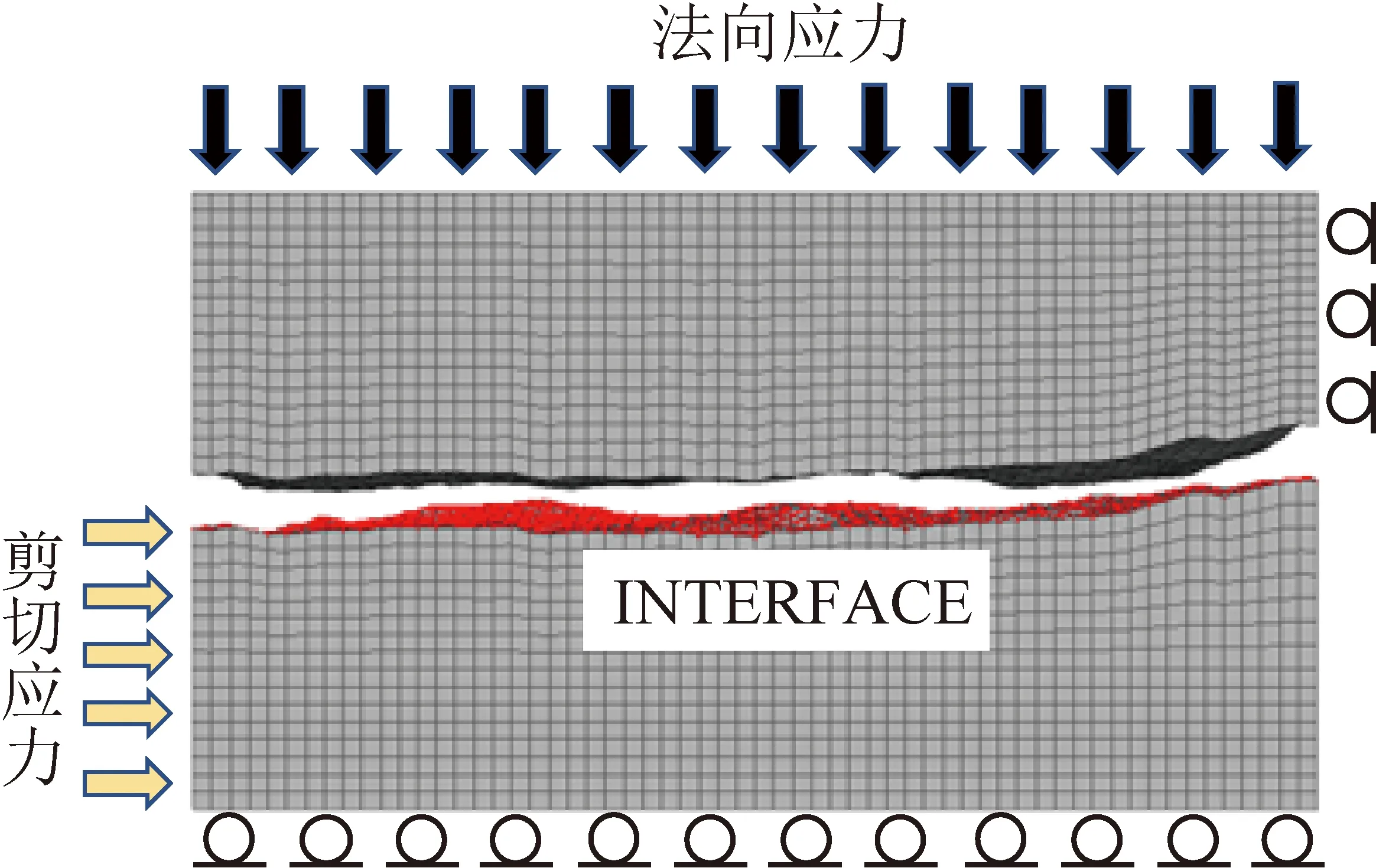
圖8 巖石粗糙結構面剪切數值模型Fig.8 Numerical model for joints shear of rough rock discontinuity

表1 數值模型中的物理力學參數

2.3 對比驗證

采用室內試驗和數值模擬得到的結構面剪切應力-剪切位移對比曲線如圖9所示。

由圖9可以看出，修正模型的剪切應力曲線與試驗曲線在不同法向應力條件下都匹配較好，尤其是J1和J2結構面，J3結構面在位移軟化階段模擬應力略大于試驗結果。這是由于J3結構面的粗糙度系數大，需建立更精細的網格來還原表面形貌特征，以減小模擬與試驗的誤差，但這將需要更長的運算時間。

為進一步驗證數值模擬的正確性，將室內試驗和數值模擬得到的結構面表面特征進行對比。由于試驗中無法監測結構面的接觸狀態，因此，采用試驗完成后的結構面破壞圖與數值模擬的結構面接觸圖。以法向應力2 MPa的J3結構面為例，圖10(a)為室內試驗中的結構面的表面破壞特征示意，其中紅色圈出的區域為剪切破壞區；圖10(b)為數值模擬中結構面接觸分布特征示意，其中不同顏色代表不同的滲透深度，具體在第3.1節中詳述。可以看出，兩圖分布整體上較為接近，但數值模擬得到的接觸區域小于室內試驗中結構面的破壞區域，這是合理的，因為結構面破壞后不可恢復，而接觸區域卻一直隨著剪切位移發生改變。因此，從結構面破壞情況來看，該模擬方法能夠較好地模擬結構面剪切的動態接觸特征。

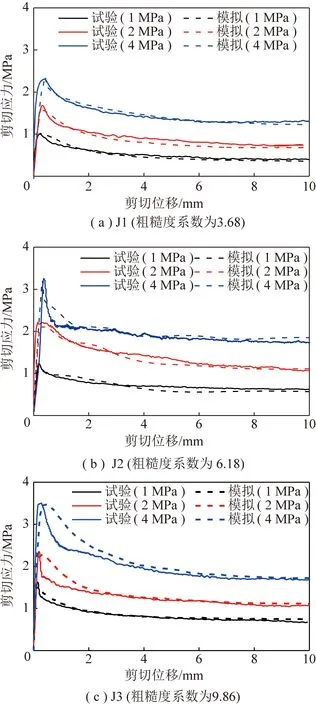
圖9 不同粗糙度巖石結構面剪切應力-剪切位移對比曲線Fig.9 Comparison of shear displacement-shear stress curves of rock discontinuity with different joint roughness coefficients

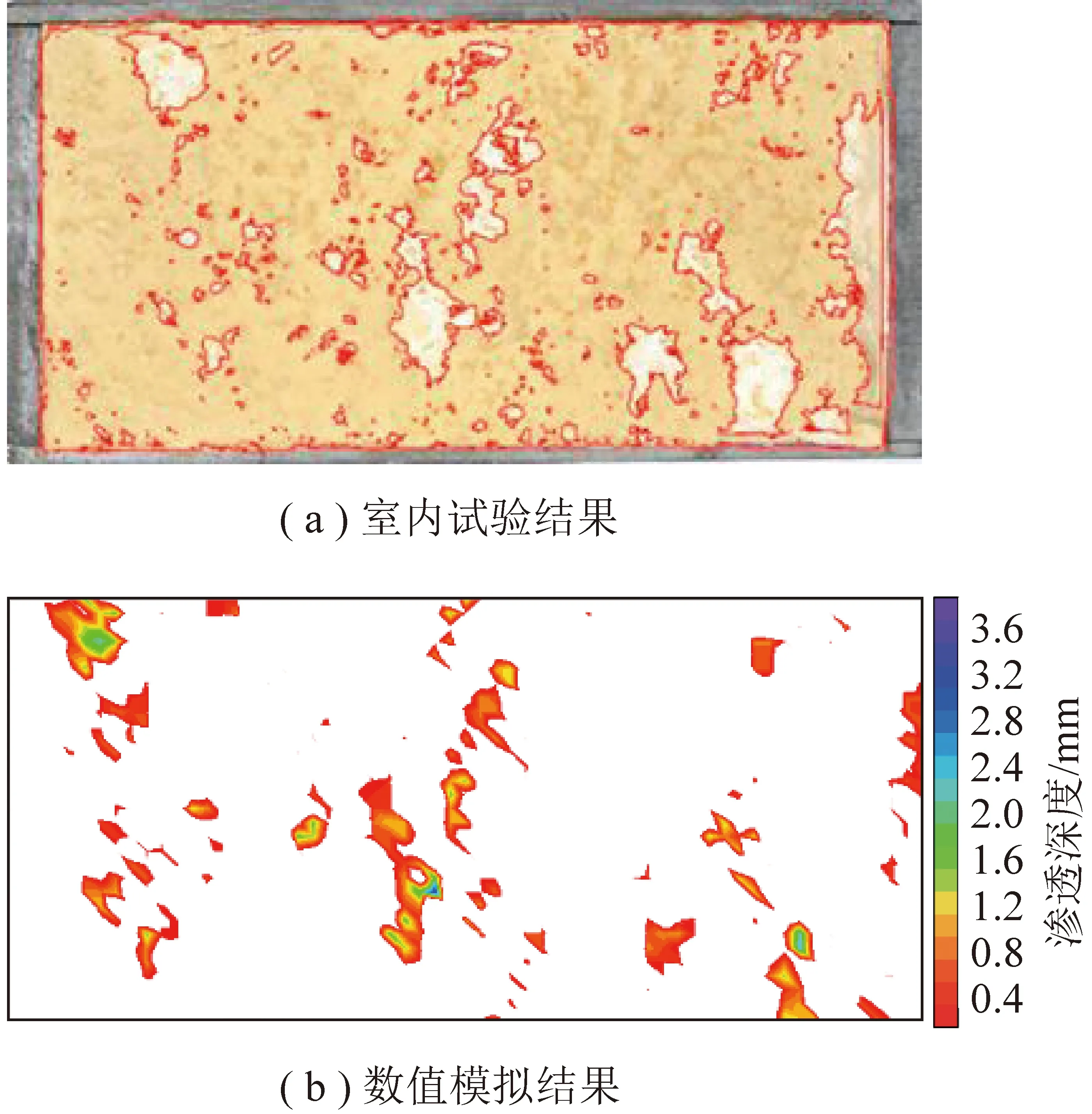
圖10 巖石結構面剪切破壞表面特征對比Fig.10 Comparison of surface characteristics of rock discontinuity shear failure

3 數值模擬結果與分析

3.1 接觸面積特征及其演化規律

FLAC中結構面的接觸狀態由INTERFACE的節點和單元體表面的相對位置關系，即模型上部與下部對應節點的高程變化(滲透值)所決定。當INTERFACE的節點穿透單元體表面與單元體重疊，即>0時，INTERFACE單元被認為接觸。已有學者指出這些重疊部分可以合理地表示剪切試驗中的接觸區域。以法向應力2 MPa的J3結構面剪切位移為3 mm時的接觸情況為例進行說明。圖11(a)為結構面的接觸分布；圖11(b)為接觸的滲透深度，滲透深度為負值表示結構面單元分離；滲透深度大于0表示結構面單元接觸。每個INTERFACE節點都關聯一定的面積，因此可以采用接觸的INTERFACE節點數與總的INTERFACE節點數之比來定義結構面的接觸面積比。

圖11 巖石結構面接觸分布及其滲透深度Fig.11 Contact distribution and penetration depth of rock discontinuity

剪切過程中結構面接觸面積分布演化特征如圖12所示，其中上方彩色圖為不同剪切位移時INTERFACE的接觸分布，白色部分表示分離區域，彩色部分表示不同接觸滲透深度的區域(由于滲透深度大于4的數量較少，因此將滲透深度大于4的區域均設為紫色)；藍色曲線代表接觸面積比隨剪切位移增大的變化規律。可以看出，隨著剪切位移增大，結構面的接觸面積減小，計算得到的接觸面積比也不斷減小，但最大滲透深度卻不斷增加。剪切位移0,0.3,1,3,5,7,10 mm時所對應的接觸面積比分別為100%,67.85%,36.70%,24.54%,18.67%,15.34%和11.69%，對應的最大滲透深度分別為0,0.14,0.40,1.13,1.79,2.42,3.35 mm。值得注意的是，結構面接觸面積顯著減小主要發生在剪切位移0～1 mm，當剪切位移大于1 mm后，減小的速度呈現出顯著的下降趨勢，節理接觸面積比降低很緩慢，這與以往諸多的研究結論相同。

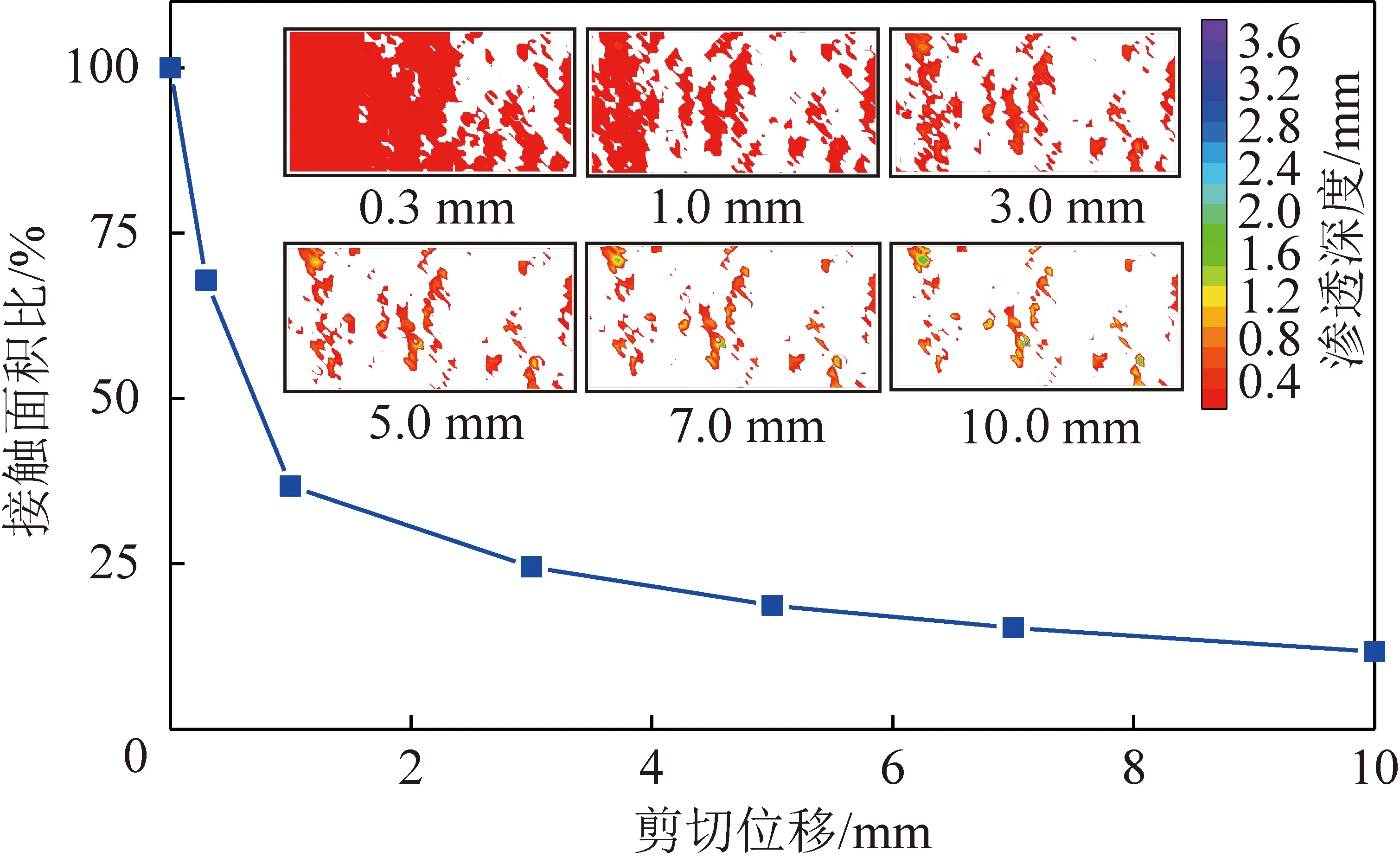
圖12 剪切過程中巖石結構面接觸面積分布及其演化特征Fig.12 Contact area distribution of rock discontinuity during shearing and its evolution characteristic

圖13(a)為不同法向應力條件下J3結構面的接觸特征，包括接觸分布圖和滲透深度頻率曲線。由其中的接觸分布圖可以直觀看出，隨著法向應力的增大，不僅結構面的接觸面積增大，結構面的最大滲透深度也增大。不同法向應力條件下的滲透深度頻率曲線形態相近，但隨著法向應力的增大，曲線整體上向右偏移，也可證明上述結論。計算得到法向應力為1,2,4 MPa時結構面的接觸面積比分別為6.98%,11.69%,21.47%，如圖13(b)所示，隨著法向應力的增大，結構面接觸面積比呈線性增大。結構面的最大滲透深度分別為3.02,3.35,3.68 mm。這主要是由于剪切過程中結構面的接觸區域由其表面形貌特征以及剪切方向決定。因此，不同法向應力條件下相同形貌結構面的接觸分布相似。但法向應力增大會導致凸起尖端滲透深度增大，進而造成接觸面積的增大。

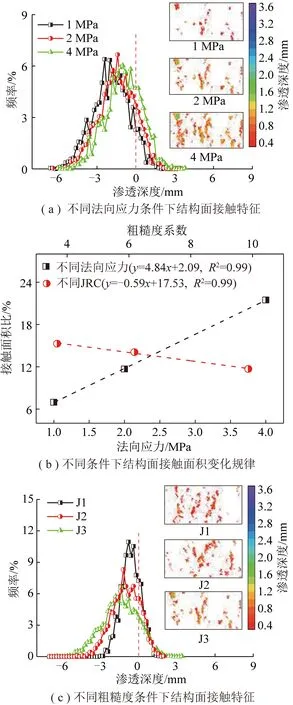
圖13 不同法向應力和不同粗糙度條件下巖石結構面接觸特征Fig.13 Contact characteristics of rock discontinuity under different normal stresses and different joint roughness coefficients conditions

如圖13(c)為法向應力為2 MPa條件下的不同粗糙度結構面的接觸特征。由其中的接觸分布圖可以直觀看出，隨著JRC的增大，結構面的接觸面積減小，但結構面的最大滲透深度增大。不同JRC條件下的滲透深度頻率曲線形態差別顯著，隨著JRC的增大，曲線高度降低，且整體上向兩側擴展，尤其是左側，這不僅表明了結構面接觸面積減小、滲透深度增加，同時也表明了結構面分離程度增加。計算得到J1，J2和J3結構面的接觸面積比分別為15.28%,14.07%和11.69%，如圖13(b)所示，隨著JRC的增大，結構面接觸面積比呈線性減小。結構面的最大滲透深度分別為1.42,1.84,3.35 mm。上述現象是由于結構面越粗糙則其剪脹變形越顯著，這會導致結構面的接觸面積減小，進而造成結構面接觸部分應力集中程度高，較大的法向應力會造成滲透深度增大。

3.2 剪切應力特征及其演化規律

結構面的接觸特征對結構面的受力分布有較大的影響。由3.1節可知，結構面的接觸面積隨著剪切運動逐漸減小，而施加在結構面的法向應力將全部作用在接觸部分上，進而導致接觸區域所受法向應力遠高于施加的法向應力，尤其是粗糙尖端的應力，可以達到巖石強度極限狀態，并導致這些凸起的失效。圖14為法向應力為2 MPa條件下J3結構面在剪切過程中的剪切應力分布及其演化特征，其中彩色圖為不同剪切位移時INTERFACE的剪切應力分布，白色部分表示剪切應力為0的區域，彩色部分表示不同大小剪切應力的區域；各曲線代表不同剪切位移條件下剪切應力的分布頻率，該曲線是利用自編FISH函數，將結構面上各節點所受剪切應力導出后統計得到的。

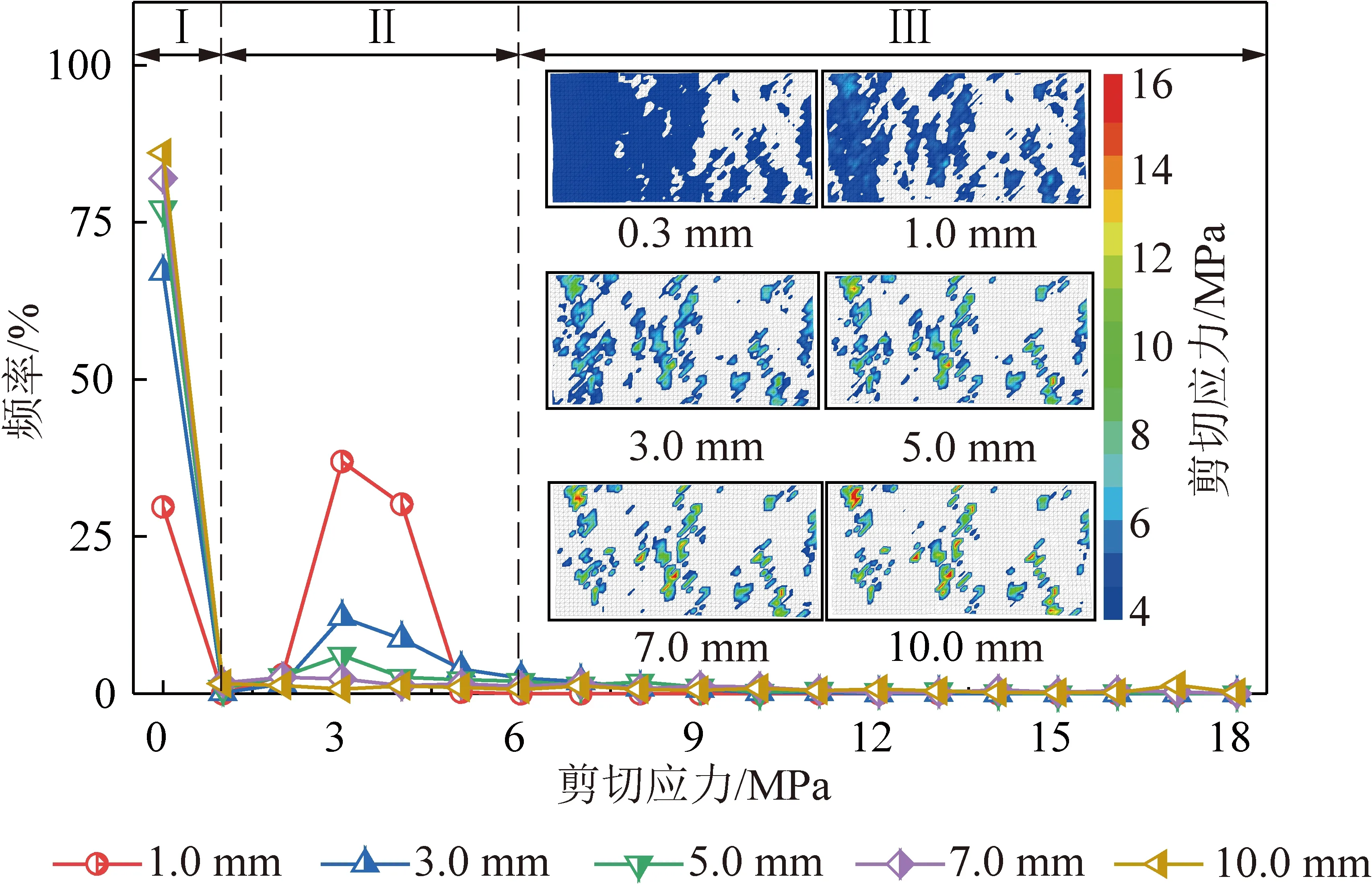
圖14 剪切過程中巖石結構面剪切應力分布及其演化特征Fig.14 Shear stress distribution of rock discontinuity during shearing and its evolution characteristic

由剪切應力分布可以看出，在剪切初期，結構面完全閉合，剪切應力分布均勻。隨著剪切位移增加，在結構面接觸分布變化的影響下，結構面剪切應力集中現象越來越顯著。剪切位移0,0.3,1,3,5,7,10 mm所對應的結構面最大剪切應力分別為0,3.46,5.37,15.07,17.81,17.81,17.81 MPa。當剪切位移超過5 mm后，隨著剪切位移的增大，結構面各單元的最大剪切應力不再增大，但最大剪切應力的分布范圍有所增加。由前文INTERFACE模型修正部分可知，當接觸部分所受的法向應力超過其抗壓強度，會導致其發生法向壓破壞，結構面所受法向應力不會超過巖石的抗壓強度，且此時已處于殘余階段。結構面抗剪強度由結構面摩擦所提供，當摩擦角一定時，即會產生最大剪切應力。隨著剪切的進行，結構面接觸范圍進一步減小，接觸部分應力集中增加，結構面發生法向壓破壞的范圍增大，進而導致最大剪切應力的范圍增大。

由不同剪切位移條件下結構面剪切應力的分布頻率曲線可以看出，曲線可以分為低剪切應力區Ⅰ(小于1 MPa)、中剪切應力區Ⅱ(1～6 MPa)和高剪切應力區Ⅲ(大于6 MPa)3個區域。在低剪切應力區內，隨著剪切位移增加，節點剪切應力為0的單元的出現頻率增大，即結構面分離區域增多，但剪切位移越大變化則越不明顯，這是由接觸面積變化導致的，與前述接觸面積的變化規律相一致。剪切位移為0.3,1,3,5,7,10 mm時，剪切應力為0的單元的頻率分別為2.38%,29.72%,67.05%,77.10%,81.97%和86.04%。在中剪切應力區內，隨著剪切位移增加，區域內曲線凸起程度不斷降低。這是由于剪切位移較小時，結構面接觸面積較大，應力集中現象不明顯，各單元的剪切應力大都分布在結構面平均剪切應力附近，隨著接觸面積減小，一方面剪切應力為0的單元數量增加，另一方面應力集中導致高剪切應力的單元數量增加，因而該區域的分布頻率顯著降低。在高剪切應力區內，剪切應力分布頻率曲線近似水平，剪切位移超過3 mm后，隨著剪切位移增加曲線變化不顯著。

圖15(a)為不同法向應力條件下的結構面剪切應力分布特征。可以看出，在結構面接觸分布的影響下，隨著法向應力的增大，結構面剪切應力分布范圍增大，且結構面高剪切應力的分布范圍也隨之增大，這是由于隨著法向應力的增大，結構面兩側巖塊嵌入程度更深導致的。剪切應力分布范圍的增大和高剪切應力分布范圍的增大，是結構面剪切應力隨法向應力增大而增大的根本原因。

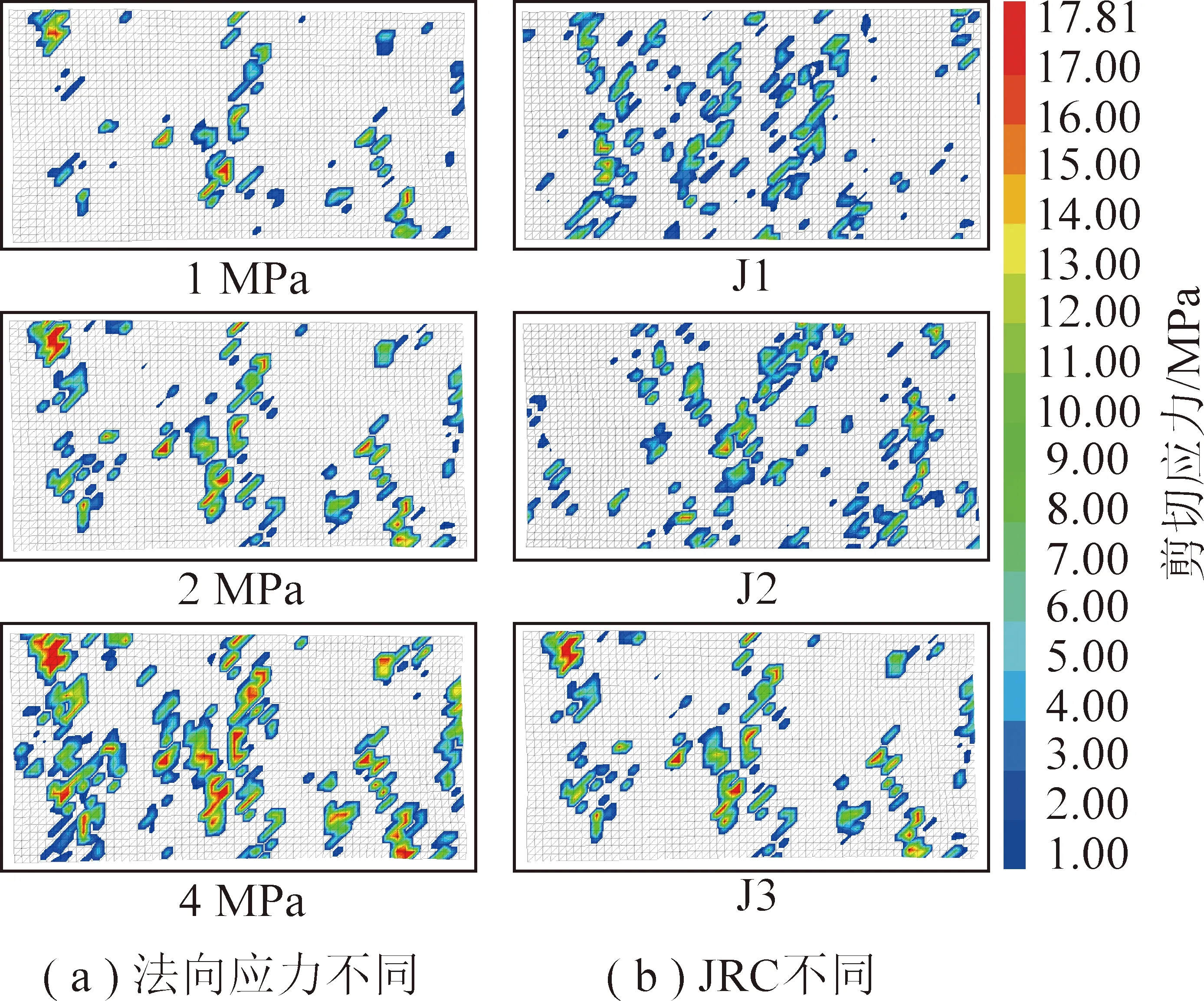
圖15 不同法向應力和不同JRC條件下巖石結構面剪切應力分布特征Fig.15 Shear stress distribution characteristics of rock discontinuity under different normal stresses and different JRCs

圖15(b)為J1，J2和J3結構面在法向應力為2 MPa條件下的剪切應力分布特征。可以看出，在結構面接觸分布的影響下，隨著JRC的增加，結構面的接觸面積減小，但高剪切應力的分布范圍顯著增大，這是由于隨著JRC的增大，結構面兩側巖塊的嵌入程度更深導致的。剪切應力分布范圍對結構面剪切應力影響不明顯，高剪切應力分布范圍的增大是結構面剪切應力隨JRC增大而增大的根本原因。

3.3 結構面接觸與表面形貌的關系

GRASSELLI等研究表明，結構面的潛在接觸面積與其表面的傾角有關，認為結構面接觸區域可以簡化為只考慮面向剪切方向且比臨界視傾角更大的區域，并提出了新的粗糙度指標來描述接觸面積比與臨界視傾角的函數關系為

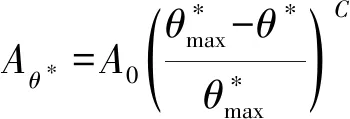
(8)

由式(8)可以看出，結構面的接觸分布與結構面的傾角分布、臨界視傾角有著密切聯系。圖16為J3結構面在剪切前的視傾角分布，其中白色部分的視傾角小于0°，彩色部分的視傾角大于0°。可以看出，其與圖12中的接觸區域分布規律大致相同。眾多學者研究表明，該指標能夠較好地描述結構面形貌與接觸的關系。

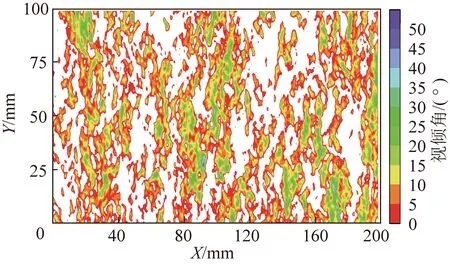
圖16 巖石結構面視傾角分布特征Fig.16 Apparent dip angle distribution characteristic of rock joint

結構面的接觸面積會隨著結構面的剪切位移、法向應力和粗糙度變化，因此臨界視傾角在不同條件下的取值也不同。筆者借助數值模擬結果對不同條件下臨界視傾角取值的變化規律進行探究，即通過3.1節得到結構面的接觸面積比，反算出不同條件下的臨界視傾角。其中，J1，J2和J3結構面的擬合參數參照文獻[13]的計算方法，其值分別為2.52，2.81，2.34。

圖17為法向應力2 MPa條件下J1，J2和J3結構面在不同剪切位移時的臨界視傾角。可以看出，從剪切位移為1 mm到剪切結束，J1，J2和J3結構面視傾角的變化區間分別為2.31°～7.60°，3.08°～9.19°和4.92°～14.33°，分別增長了5.29°，6.11°和9.41°。不同粗糙度結構面的臨界視傾角都隨著剪切位移的增大而增大，臨界視傾角與剪切位移呈冪函數關系，隨著剪切位移增加，臨界視傾角的增加速度逐漸變緩。隨著JRC增大，剪切過程中結構面臨界視傾角的變化范圍增大。

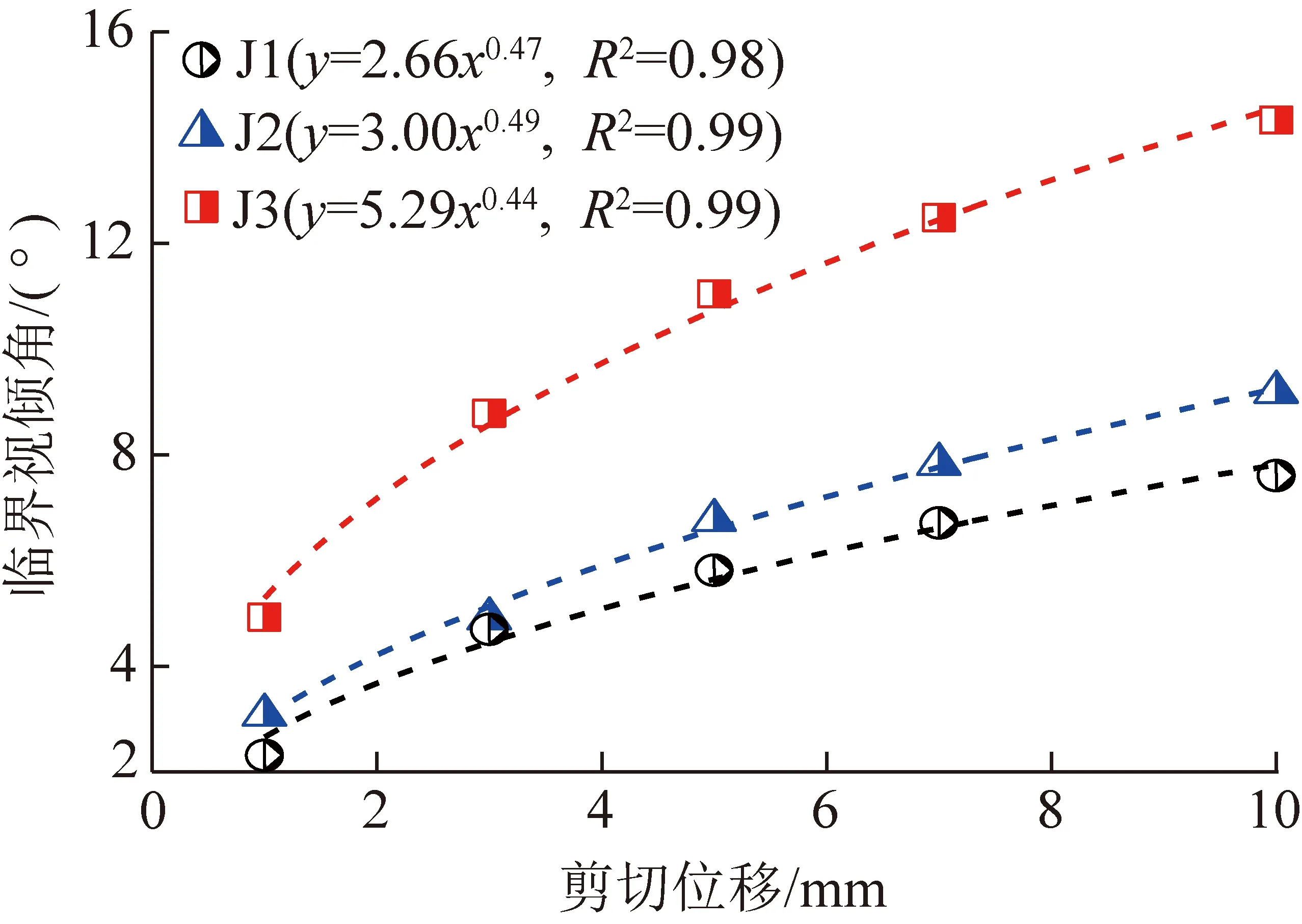
圖17 剪切過程中巖石結構面臨界視傾角演化規律Fig.17 Evolution of the threshold apparent dip angle of rock discontinuity during shearing

圖18(a)為不同法向應力條件下結構面所對應的臨界視傾角。可以看出，J1，J2和J3結構面的臨界視傾角變化區間分別為9.90°～4.90°，12.33°～5.76°和17.29°～9.92°，分別減小了5.00°，6.57°和7.37°。

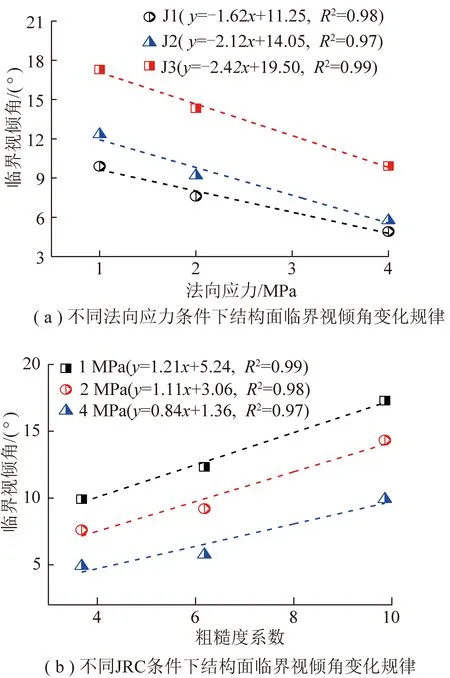
圖18 不同法向應力和不同JRC條件下巖石結構面臨界視傾角變化規律Fig.18 Evolution of the threshold apparent dip angle of rock discontinuity under different normal stresses and different JRCs

臨界視傾角與結構面法向應力呈負線性關系，不同粗糙度結構面的臨界視傾角都隨著法向應力的增大而減小，且隨著JRC的增大，曲線斜率增大，即表明隨著JRC增大，法向應力對臨界視傾角的影響增大。圖18(b)為不同JRC條件下結構面所對應的臨界視傾角。可以看出，法向應力分別為1,2,4 MPa的結構面的臨界視傾角變化區間分別為9.90°～17.29°，7.60°～14.33°和4.90°～9.92°，分別增大了7.39°，6.73°，5.09°。不同法向應力結構面的臨界視傾角都隨著JRC的增大而增大，臨界視傾角與JRC呈負線性關系，且隨著法向應力的增大，曲線斜率增大。即表明隨著法向應力增大，JRC對臨界視傾角的影響增大。

通過對不同條件下結構面臨界視傾角變化規律的研究，可以預測結構面在不同條件下的接觸分布情況以及接觸面積比，進而建立合理的結構面粗糙度指標以及相關的抗剪強度準則。為此，需要進一步探討結構面剪切應力與接觸的關系。

3.4 結構面剪切應力與接觸的關系

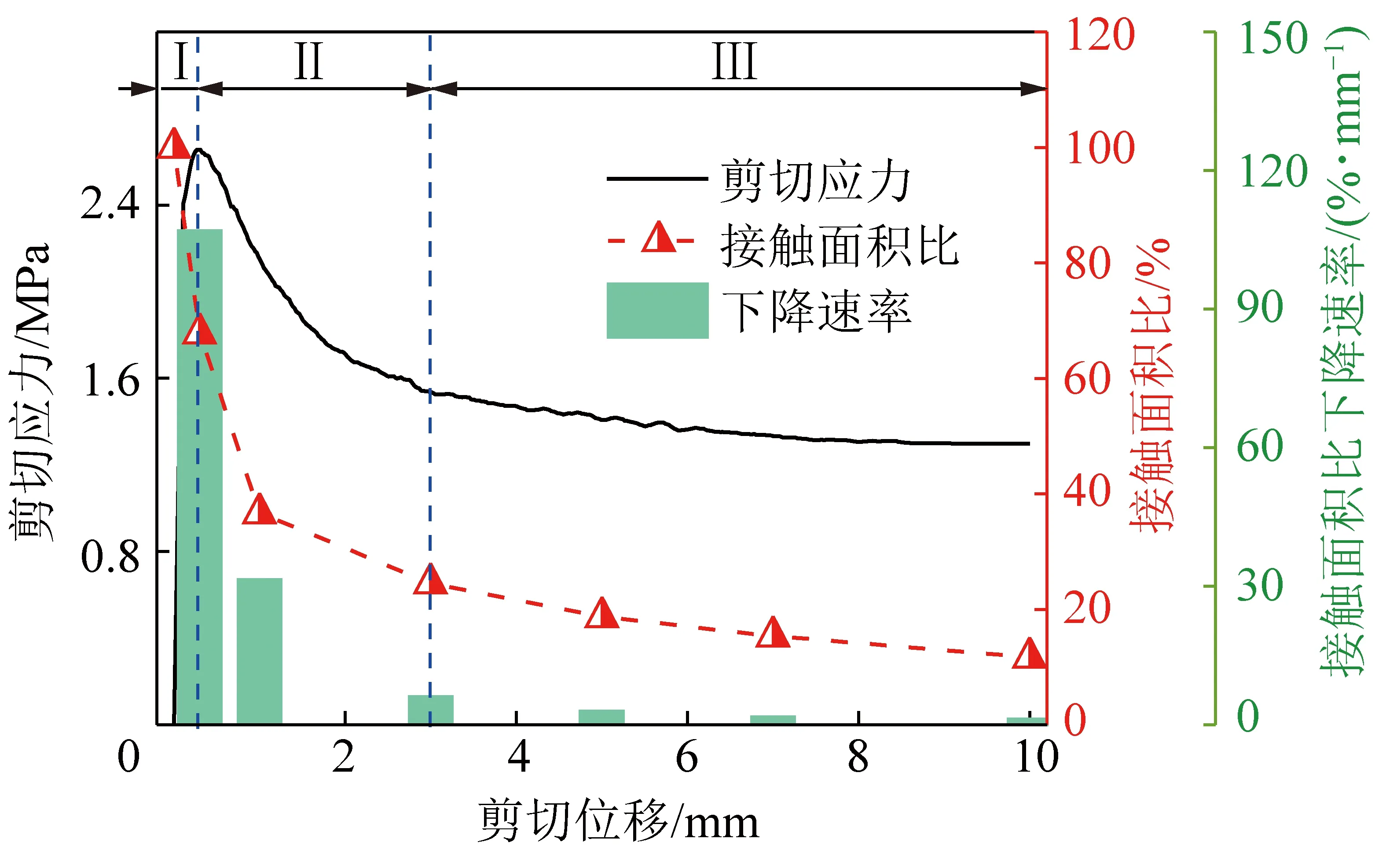
圖19 巖石結構面剪切應力、接觸面積比及接觸面積比下降速率演化規律Fig.19 Evolution of shear stress,contact area ratio and its decline rate of rock discontinuity

結構面的剪切應力由其表面接觸部分提供。法向應力為2 MPa條件下J3結構面剪切過程中的剪切應力、接觸面積比以及接觸面積比下降速率如圖19所示。可以看出，在剪切應力峰值前，隨著接觸面積比的下降，結構面剪切應力仍然繼續增大，而在剪切應力峰值后，接觸面積比曲線與結構面的剪切應力曲線形態較為一致，2者呈正相關關系。這是由于在剪切應力峰值前，結構面表面凸起尚未破壞，結構面剪切應力由這些凸起提供，凸起處于彈性階段，結構面的剪切應力隨著剪切位移的增加而增加，而當凸起開始破壞后，即進入峰后階段，結構面剪切應力由少部分未破壞的凸起和接觸部分的摩擦提供，并且當剪切位移進一步增大時，結構面接觸中的凸起大部分被破壞，結構面剪切應力主要由接觸部分的摩擦提供，在峰后階段隨著結構面接觸面積減少，結構面剪切應力相應減小。因此，在剪切應力峰值后，剪切應力迅速下降的原因不僅是由于結構面表面凸起的破壞，而且還與結構面接觸面積的變化有較強的相關性。

由前文分析可知，結構面接觸面積比下降速率可以一定程度上反映結構面發生破壞的情況。由圖19中綠色柱可以看出，在不同剪切位移階段結構面接觸面積比下降速率不同，在剪切位移為0.3,1,3,5,7,10 mm時其下降速率分別為83.33%/mm,38.60%/mm,6.08%/mm,2.93%/mm,1.67%/mm,1.22%/mm。即表明結構面接觸面積比在彈性階段Ⅰ下降最快，其次是在位移-軟化階段Ⅱ，殘余階段Ⅲ下降最慢。這是由于，在彈性階段內，結構面表面凸起未發生破壞，巖塊沿著凸起爬坡較為容易，接觸面積比迅速下降，但由于該階段剪切位移較小，接觸面積比仍較大；位移軟化階段，由于表面凸起開始被啃斷，接觸面積比下降速率有所下降，但仍處于一個較高水平，由于該階段剪切位移較大，接觸面積比下降到了較低水平；殘余階段，結構面表面的潛在啃斷的凸起基本都已被啃斷，巖塊運動爬坡現象不明顯，而是以摩擦滑移為主，因而結構面接觸面積比下降速率變得非常低。

總地來說，上述研究闡明了剪切過程中以及不同法向應力和不同粗糙度條件下的巖體結構面的動態接觸特征，揭示了結構面表面形貌-接觸特征-剪切應力3者間的關系，深化了對剪切過程中剪切應力演化規律及其機理的認識，可為預測不同條件下結構面的剪切特性提供一定規律性參考。

4 結 論

(1)FLAC自帶INTERFACE模型無法很好地模擬結構面峰后剪切行為，是由于結構面凸起未啃斷導致黏聚力和法向應力偏大。通過修正INTERFACE破壞單元的黏聚力和法向剛度的等效方法，可很好地模擬結構面的損傷破壞行為。

(2)隨剪切位移增大，結構面接觸面積逐漸減小，最大滲透深度不斷增加；隨法向應力增大，結構面接觸面積和滲透深度都增大；隨JRC增大，結構面接觸面積減小，最大滲透深度增大。

(3)隨法向應力增大，結構面剪切應力分布范圍增大，且高剪切應力分布范圍也增大；隨JRC增加，結構面剪切應力分布范圍減小，高剪切應力分布范圍顯著增大。

(4)結構面臨界視傾角隨剪切位移呈冪函數關系增大；JRC相同時，臨界視傾角隨法向應力的增大而減小；法向應力相同時，臨界視傾角隨JRC的增大而增大。

(5)結構面剪切應力降低與其接觸面積變化有較強的相關性，結構面的接觸面積比在彈性階段下降最快，位移-軟化階段次之，殘余階段最慢。

[1] 班力壬，戚承志，單仁亮，等. 節理峰前剪切剛度軟化模型及其影響因素分析[J]. 煤炭學報，2018,43(10):2765-2772.

BAN Liren,QI Chengzhi,SHAN Renliang,et al. Pre-peak shear constitutive model considering the softening shear stiffness and its influencing factors[J]. Journal of China Coal Society,2018,43(10):2765-2772.

[2] 楊小彬,周杰,宋義敏,等. 循環加載巖石界面滑移位移演化特征試驗研究[J]. 煤炭學報,2019,44(10):3041-3048.

YANG Xiaobin,ZHOU Jie,SONG Yimin,et al．Evolution characteristics of sliding displacement of rock INTERFACE under cyclic loading[J]．Journal of China Coal Society,2019,44(10):3041-3048.

[3] JU Y,WAN C B,REN Z Y,et al. Quantification of continuous evolution of full-field stress associated with shear deformation of faults using three-dimensional printing and phase-shifting methods[J]. International Journal of Rock Mechanics and Mining Sciences,2020,126:1365-1609.

[4] BARTON N. The shear strength of rock and rock joints[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1976,13(9):255-279.

[5] BARTON N,BANDIS S,BAKHTAR K. Strength,deformation and conductivity coupling of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1985,22(3):121-140.

[6] XIA C C,TANG Z C,XIAO W M,et al. New peak shear strength criterion of rock joints based on quantified surface description[J]. Rock Mechanics and Rock Engineering,2014,47(2):387-400.

[7] YANG J,RONG G,HOU D,et al. Experimental study on peak shear strength criterion for rock joints[J]. Rock Mechanics and Rock Engineering,2016,49(3):821-835.

[8] KARAMI A,STEAD D. Asperity degradation and damage in the direct shear test:A hybrid FEM/DEM approach[J]. Rock Mechanics and Rock Engineering,2008,41(2):229-266.

[9] ASADI M S,RASOULI V,BARLA G. A laboratory shear cell used for simulation of shear strength and asperity degradation of rough rock fractures[J]. Rock Mechanics and Rock Engineering,2013,46(4):683-699.

[10] BAHAADDINI M,HAGAN P C,MITRA R,et al. Experimental and numerical study of asperity degradation in the direct shear test[J]. Engineering Geology,2016,204:41-52.

[11] ZHAO Z H,PENGP H,WU W,et al. Characteristics of shear-induced asperity degradation of rock fractures and implications for solute retardation[J]. International Journal of Rock Mechanics and Mining Sciences,2018,105:53-61.

[12] MENG F Z,ZHOU H,WANG Z Q,et al. Characteristics of asperity damage and its influence on the shear behavior of granite joints[J]. Rock Mechanics and Rock Engineering,2018,51(2):429-449.

[13] GRASSELLI G. Shear strength of rock joints based on quantified surface description[D]. Switzerland:école Polytechnique Fédérale de Lausanne,2001.

[14] FATHI A,MORADIAN Z,RIVARD P,et al. Geometric effect of asperities on shear mechanism of rock joints[J]. Rock Mechanics and Rock Engineering,2016,49(3):801-820.

[15] XIAO W M,XIAO C C,WANG W,et al. Contact algorithm for determining aperture evolution of rock fracture during shearing[J]. International Journal of Geomechanics,2016,16(3):04015070.

[16] MENG F Z,ZHOU H,LI S J,et al. Shear behaviour and acoustic emission characteristics of different joints under various stress levels[J]. Rock Mechanics and Rock Engineering,2016,49(12):4919-4928.

[17] 崔國建,張傳慶,韓華超,等. CNL及CNS條件下結構面剪切特性試驗研究[J]. 巖石力學與工程學報,2019,38(S2):3384-3392.

CUI Guojian,ZHANG Chuanqing,HAN Huachao,et al. Experiment study on shear behavior of artificial joint under CNL and CNS boundary conditions[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(S2):3384-3392.

[18] 尹乾,靖洪文,孟波,等. CNL 和 CNS 邊界條件下砂巖宏細觀剪切力學特性[J]. 采礦與安全工程學報,2020,38(3):615-624.

YIN Qian,JING Hongwen,MENG Bo,et al. Macroscopic and microscopic shear mechanical properties of sandstone under CNL and CNS boundary conditions[J]. Journal of Mining & Safety Engineering,2020,38(3):615-624.

[19] FAN W C,CAO P,LONG L. Degradation of joint surface morphology,shear behavior and closure characteristics during cyclic loading[J]. Journal of Central South University,2018,25(3):653-661.

[20] 劉新榮,鄧志云,劉永權,等. 巖石節理峰前循環直剪試驗顆粒流宏細觀分析[J]. 煤炭學報,2019,44(7):2103-2115.

LIU Xinrong,DENG Zhiyun,LIU Yongquan,et al. Macroscopic and microscopic analysis ofparticle flow in pre-peak cyclic direct shear test of rock joint[J]. Journal of China Coal Society,2019,44(7):2103-2115.

[21] BARTON N,CHOUBEY V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics Felsmechanik Mécanique des Roches,1977,10(1-2):1-54.

[22] TSE R,CRUDENC D M. Estimating joint roughness coefficients[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1979,16(5):303-307.

[23] GE Y F,KULATILAKE P H S W,TANG H,et al. Investigation of natural rock joint roughness[J]. Computers and Geotechnics,2014,55:290-305.

[24] ZHANG G C,KARAKUS M,TANG H,et al. A new method estimating the 2D Joint roughness coefficient for discontinuity surfaces in rock masses[J]. International Journal of Rock Mechanics and Mining Sciences,2014,72:191-198.

[25] 唐志成,夏才初,宋英龍. 粗糙節理的峰值抗剪強度準則[J]. 巖土工程學報,2013,35(3):571-577.

TANG Zhicheng,XIA Caichu,SONG Yinglong. New peak shear strength criteria for roughness joints[J]. Chinese Journal of Geotechnical Engineering,2013,35(3):571-577.

[26] PARK J W,SONG J J. Numerical method for the determination of contact areas of a rock joint under normal and shear loads[J]. International Journal of Rock Mechanics and Mining Sciences,2013,58:8-22.

[27] LIU X G,ZHU W C,YU Q L,et al. Estimating the joint roughness coefficient of rock joints from translational overlapping statistical parameters[J]. Rock Mechanics and Rock Engineering,2019,52(3):753-769.

[28] ZHAO J. Matching Matching Coefficient (JMC)[J]. International Journal of Rock Mechanics and Mining Sciences,1997,34:173-178.

[29] GRASSELLI G. Manuel rocha medal recipient shear strength of rock joints based on quantified surface description[J]. Rock Mechanics and Rock Engineering,2006,39(4):295-314.

[30] 唐志成,夏才初,宋英龍,等. Grasselli節理峰值抗剪強度公式再探[J]. 巖石力學與工程學報,2012,31(2):356-364.

TANG Zhicheng,XIA Caichu,SONG Yinglong,et al. Discussion about Grasselli’s peak shear strength criterion for rock joints[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(2):356-364.

[31] 楊潔,榮冠,程龍,等. 節理峰值抗剪強度試驗研究[J]. 巖石力學與工程學報,2015,34(5):884-894.

YANG Jie,RONG Guan,CHENG Long,et al. Experimental study of peak shear strength of rock joints [J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(5):884-894.

[32] 陳曦,曾亞武,孫翰卿,等. 基于Grasselli形貌參數的巖石節理初始剪脹角新模型[J]. 巖石力學與工程學報,2019,38(1):133-152.

CHEN Xi,ZENG Yawu,SUN Hanqing,et al. A new model of the initial dilatancy angle of rock joints based on Grasselli′s morphological parameters[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(1):133-152.

[33] 劉燕強. 巖石結構面剪切全過程的可視化試驗方法及試驗驗證[D]. 紹興:紹興文理學院,2019.

LIU Yanqiang. Visual test method and experimental verification for the whole shear process of rock structural plane[D].Shaoxing; Shaoxing University of Arts and Sciences, 2019.

[34] LIU X G,ZHU W C,LI L K. Numerical shear tests on the scale effect of rock joints under CNL and CND conditions[J]. Advances in Civil Engineering,2020,2020:1-15.

[35] MAHDI S,ABBAS T. A numerical study to investigate the influence of surface roughness and boundary condition on the shear behaviour of rock joints[J]. Bulletin of Engineering Geology and the Environment,2020,79(5):2483-2498.

[36] 郭冠龍. 昊錦塬煤礦含充填節理巷道圍巖控制技術研究 [D]. 徐州：中國礦業大學,2015.

GUO Guanlong. Controlling technology of roadway surrounding rock containing infilled joints in Haojinyuan coal mine[D].Xuzhou: China University of Mining and Technology, 2015.

[37] 劉新榮,許彬,周小涵,等. 軟硬互層巖體結構面宏細觀剪切力學特性研究[J]. 煤炭學報,2021,46(9):2895-2909.

LIU Xinrong,XU Bin,ZHOU Xiaohan,et al. Investigation on the macro-meso shear mechanical properties of soft-hard interbedded rock discontinuity[J]. Journal of China Coal Society,2021,46(9):2895-2909.

[38] NGUYEN V M,KONIETZKY H,FRUHWIRT T. New meth odology

to characterize shear behavior of joints by combination of direct shear box testing and numerical simulations[J]. Geotechnical and Geological Engineering,2014,32(4):829-846.

[39] DANG W G,WU W,KONIETZKY H,et al. Effect of shear-induced aperture evolution on fluid flow in rock fractures[J]. Computers and Geotechnics,2019,114:103-152.

[40] 楊建平,陳衛忠,黃勝. 一種巖石統計損傷本構模型的研究[J]. 巖土力學,2010,31(S2):7-11.

YANG Jianping,CHEN Weizhong,HUANG Sheng. Study of a statistic damage constitutive model for rocks[J]. Rock and Soil Mechanics,2010,31(S2):7-11.

[41] ITASCA. FLAC-fast lagrangian analysis of continua in 3 dimensions-theory and background[M]. Minnesota:Itasca Consulting Group Inc,2012.

[42] JING L. Numerical modelling of jointed rock masses by distinct element method for two-and three-dimensional problems[D]. Lulea，Sweden： Lulea University of Technology，1990.

[43] LIAO Z Y,REN M,TANG C A,et al. A three-dimensional damage-based contact element model for simulating the interfacial behaviors of rocks and its validation and applications[J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources,2020,6(3)1-21.

[44] ZHU W C,WEI C H. Numerical simulation on mining-induced water inrushes related to geologic structures using a damage-based hydromechanical model[J]. Environmental Earth Sciences,2011,62(1):43-54.

[45] LIANG Z Z,XING H,WANG S Y,et al. A three-dimensional numerical investigation of the fracture of rock specimens containing a pre-existing surface flaw[J]. Computers and Geotechnics,2012,45:19-33.

[46] 蔣宇靜,張孫豪,欒恒杰,等. 恒定法向剛度邊界條件下錨固節理巖體剪切特性試驗研究[J]. 巖石力學與工程學報,2021,40(4):663-675.

JIANG Yujing,ZHANG Sunhao,LUAN Hengjie,et al. Experimental study on shear characteristics of bolted rock joints under constant normal stiffness boundary conditions[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(4):663-675.

[47] JIANG Y,XIAO J,TANABASHI Y,et al. Development of an automated servo-controlled direct shear apparatus applying a constant normal stiffness condition[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(2):275-286.

[48] 陳曦,曾亞武. 一個新的巖石節理三維粗糙度指標——基于Grasselli模型[J]. 巖土力學,2021，42(3):1-13.

CHEN Xi,ZENG Yawu. A new three-dimensional roughness metric based on Grasselli’s model[J]. Rock and Soil Mechanics,2021，42(3):1-13.