基于孔特征的弱紋理堆疊工件識別

王書宇，田建艷，蔡文站，李濟甫，王素鋼，李麗宏

太原理工大學 電氣與動力工程學院，太原 030024

抓取和放置工件是工業環境下機器人系統的主要任務之一，視覺伺服是機器人系統的重要控制手段[1]，采用圖像技術對工件進行識別在現代化智能生產線上具有重要的意義[2]。

圖像紋理是一種通過像素及其周圍空間鄰域的灰度分布來表現的局部紋理信息，傳統的目標識別算法根據圖像的顏色紋理建立具有較高辨識度的局部特征描述子，如SIFT、SURF、ORB等，然后進行特征匹配從而實現目標檢測[3]。但工業環境中大部分工件為弱紋理工件，如PVC零件、金屬零件等，對于這些弱紋理工件，其表面紋理缺乏，紋理像素較大，并且紋理像素之間的色調差異較小，導致傳統的局部特征描述子辨識度較低，無法建立從場景到模型的穩定特征點匹配關系，對于弱紋理工件識別效果不佳[4]。Rusu等[5]基于三維點云提出了快速點特征直方圖描述子（fast point feature histogram，FPFH），把關鍵點鄰域內的幾何特征轉換為多維直方圖進行描述。但點云描述符對噪聲比較敏感，描述符質量依賴于點云的質量，尤其是金屬零件等非朗伯體表面，獲取的點云數據有嚴重的缺失和形變失真，都會降低點云描述符的可靠性[6]。

模板匹配是用事先定義好的模板在輸入圖像中搜索，從而找到匹配區域的一種高級機器視覺技術，不需對大量的數據樣本進行訓練[7]。基于灰度的模板匹配對光照變化敏感，計算時間長，且不具備旋轉不變性[8]。基于形狀的模板匹配具有尺度不變性和旋轉不變性，如基于Hu矩[9]、Zernike矩、形狀上下文[10]等方法，但都需要先進行邊緣提取得到目標單獨輪廓，才能進行相似度計算，而對于堆疊的工件，由于工件之間相互遮擋，工件輪廓分割難度較大，導致識別效果不佳。吳曉軍等[11]提出了基于圖像邊緣的幾何模板匹配算法，將邊緣的梯度方向和亞像素坐標作為匹配信息，該方法對光照、遮擋和旋轉具有較強的魯棒性，但當工件堆疊時工件發生傾斜且尺度發生變化，導致目標物與模板相差較大，匹配效果較差。

當工件散亂堆疊時，對工件進行分揀則需要空間的6D位姿信息，而對于弱紋理工件，由于很難提取紋理特征進行描述，大部分方法都基于特征顯著的邊界信息，HE等[12]提出了規整化直線檢測子（complete line segment detector，CLSD）用于檢測直線輪廓，但需先對物體模型進行渲染，生成大量不同視角下的邊界特征描述子再進行匹配，計算復雜度高且精度較低。

工業零件的孔洞常作為裝配、定位、識別的特征，Li等[13]以螺釘安裝孔為基準特征用于AGV的精準定位，王青等[14]為了實現飛機大部件的最佳位姿裝配，提出一種基于制造準確度與對接深孔協調準確度的大部件位姿優化算法。由于同一工件上的孔洞在不同角度、位置、尺度以及堆疊情況下的幾何約束均保持不變，因此本文針對目前工業現場弱紋理堆疊工件識別困難的問題，著重研究帶孔弱紋理工件的識別問題，以工件表面的孔洞為特征，提出一種改進幾何模板匹配算法用于帶孔弱紋理堆疊工件識別，不需進行紋理特征的提取、樣本訓練和建立不同視角的模板，根據孔特征之間的幾何約束進行工件識別，本文以合頁為例進行工件識別，可用于機器人打磨前代替人工進行分揀。本文將從工件圖像預處理，工件孔特征提取和帶孔弱紋理工件識別三個部分對工件識別過程進行闡述。

1 工件圖像預處理

在進行孔特征提取之前，先對工件圖像進行預處理，包括工件圖像灰度化和對灰度化后的圖像進行邊緣檢測，圖1給出了預處理階段的實驗結果。

圖1 預處理階段實驗結果Fig.1 Experimental results of preprocess stage

1.1 工件圖像灰度化

工業相機采集的工件圖像是RGB彩色圖像，如圖1（a）所示為采集的原始圖像。對三個通道依次進行處理耗時較長，為了提高系統的處理速度，采用加權平均法[15]將彩色工件圖像轉變成灰度圖像以降低算法的時間復雜度：

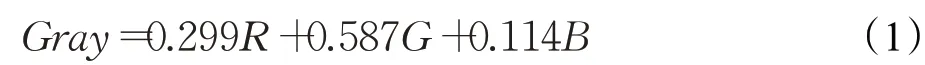
式中，R、G、B為彩色圖像中像素點的三個顏色分量；Gray為使用加權平均法灰度化后對應像素點的灰度值。

1.2 工件圖像邊緣檢測

邊緣是圖像像素值發生跳變的位置，是圖像的顯著特征之一，包含了重要的形狀信息和語義信息。與Sobel等單一邊緣檢測算法相比，Canny邊緣檢測算法所提取的邊界具有較高的連續性和聚合性，因此本文采用Canny算法進行邊緣檢測，包括高斯模糊、計算梯度幅值和方向、梯度幅值非極大值抑制與雙閾值滯后邊界跟蹤。

（1）高斯模糊

由于圖像中的噪聲通常是高頻信號，很容易被識別為偽邊緣，因此先采用高斯模糊減少噪聲，降低偽邊緣的干擾，從而提高邊緣檢測的質量。

（2）計算梯度幅值和方向

采用Sobel一階微分算子分別計算水平和垂直方向的梯度，如式（2）所示，S x和S y分別為水平和垂直方向的Sobel算子，將兩個算子分別與原圖像進行卷積，分別得到水平和垂直方向的梯度幅值矩陣G x和G y，根據式（3）和式（4）計算求得梯度幅值矩陣G和方向θ。

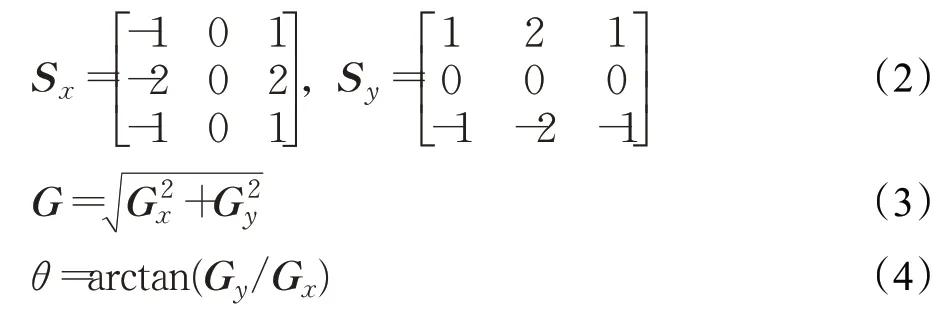
（3）梯度幅值非極大值抑制

對梯度幅值矩陣G進行非極大值抑制（non maximum suppression，NMS），沿著每個像素點的梯度方向比較前后兩點的幅值，若該點大于前后兩點則保留，否則置為0，達到保留局部最大梯度而抑制所有其他梯度值的目的，同時實現細化邊緣的效果。

（4）雙閾值滯后邊界跟蹤

采用雙閾值法確定邊界，即一個低閾值和一個高閾值來區分邊緣像素。若梯度值大于高閾值，標記為強邊緣點，為真實邊緣；若梯度值小于低閾值，直接剔除；若梯度值介于高低閾值之間，標記為弱邊緣點，并進一步判斷其8連通鄰域內是否存在強邊緣點，若存在，則這個弱邊緣點認為是真實邊緣，否則直接剔除該點。

如圖1（b）所示為Canny邊緣檢測后的圖像，可以看出，兩個工件的邊緣已經連接在一起，不易分割，而未被遮擋的孔洞輪廓清晰且未與工件邊緣相連，易于后續的孔輪廓提取以及工件識別。

2 工件孔特征提取

在工件圖像預處理的基礎上進行工件孔特征提取，首先求解每個輪廓的最小面積外接矩形（minimum area bounding rectangle，MABR），再進行幾何約束得到孔特征對應的孔輪廓，最后計算孔輪廓對應的最小外接圓（minimum enclosing circle，MEC），得到孔特征的圓心坐標，為后續工件識別奠定基礎。

2.1 工件孔輪廓提取

Canny邊緣檢測后的輪廓不僅包括孔輪廓，還包括工件的邊緣、噪聲干擾等，因此必須從所有輪廓中將孔輪廓提取出來，通過求取每個輪廓的最小面積外接矩形，并進行幾何約束，從而達到提取工件孔輪廓的目的。

2.1.1 求解輪廓凸包

在求解輪廓最小面積外接矩形時，通常先求輪廓的凸包代替輪廓的二維點集，這樣不僅可以減少點集頂點的個數，而且從根本上把一個無序的點集變成了有序的凸多邊形，形成了線性的結構，從而簡化了最小面積外接矩形的求解步驟，提高運算效率。假設單個輪廓上的所有點構成點集S，則包含S中所有點的最小凸多邊形稱為S的凸包，采用Graham算法構造每個輪廓的凸包，具體步驟為：

步驟1找到點集S中縱坐標最小的點p0，若存在多個縱坐標相同的點，選擇其中橫坐標最小的點。

步驟2以p0為參考點，分別求出p0與點集S中剩余點的極角，并從小到大排序得到點集S1={p i|pi=(x i,yi),i=0,1,…,n}。

步驟3由于凸包逆時針相鄰兩邊的向量叉乘為正值，根據式（5）依次對S1中的點進行判斷，若α為正值，則p i為凸包頂點，否則剔除該點，更新得到凸包點集S2。

2.1.2 求解輪廓最小面積外接矩形

在遍歷過程中，逆時針旋轉到下一條邊后不需要再重新掃描所有點，只要分別從上一條邊確定的三點出發，向后比較找到最大值即可，三個點的指針都只會對每個頂點訪問一次，因此整個過程的時間復雜度為O(m)。

2.1.3 幾何約束提取孔輪廓

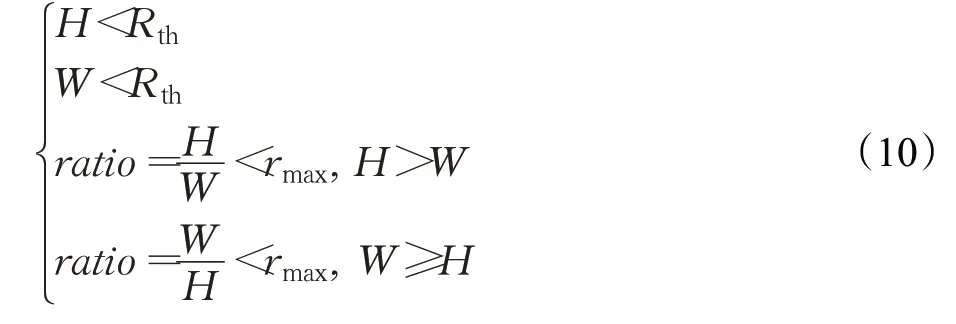
對每個輪廓對應最小面積外接矩形的寬W、高H、寬高比ratio進行幾何約束從而提取孔輪廓：式中，Rth為最小面積外接矩形寬和高的約束閾值，與相機和工件平面的高度有關，實際采集并計算多幅圖像距離，取Rth=35像素；rmax為最小面積外接矩形的寬高比約束閾值，由于最小面積外接矩形的W為x軸逆時針遇到的第一條邊，W和H無絕對的大小關系，所以需分別判斷，圓的外接矩形近似于一個正方形，寬高比接近于1，但考慮光照對圖像采集的影響以及工件堆疊時工件傾斜導致孔輪廓發生形變，寬高比發生改變，因此取rmax=2。

依次求取每個輪廓的最小面積外接矩形，并進行幾何約束，對滿足式（10）的輪廓即可認為是孔輪廓，對圖1（b）中的輪廓進行幾何約束，提取的孔輪廓如圖2所示。

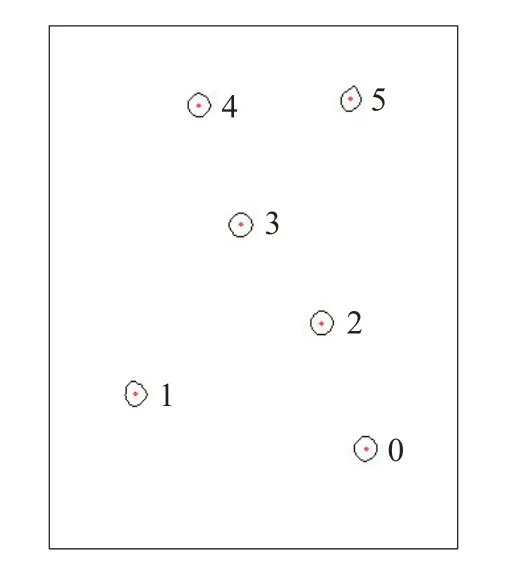
圖2 幾何約束提取的孔輪廓Fig.2 Hole contours extracted by geometric constraints

由圖2可知，對比于圖1（b），對輪廓進行幾何約束可以很好地將工件的邊緣和噪聲剔除，保留需要的孔輪廓。

2.2 求解孔輪廓圓心坐標

采用隨機增量法求解孔輪廓的最小外接圓，得到孔特征的圓心坐標，主要思想是：將孔輪廓所對應的凸包隨機排序，得到新的點集P={p0,p1,…,p n}，以p0p1為直徑作圓得到初始圓心o和半徑r，遍歷剩余的所有點，根據式（11）判斷點到當前圓心的距離，如果其余點均在該圓內，則該圓為最小外接圓，否則進行循環迭代，不斷更新圓心o和半徑r，直至遍歷所有點，得到孔輪廓的最小外接圓，同時得到最小外接圓的圓心坐標，算法流程圖如圖3所示。

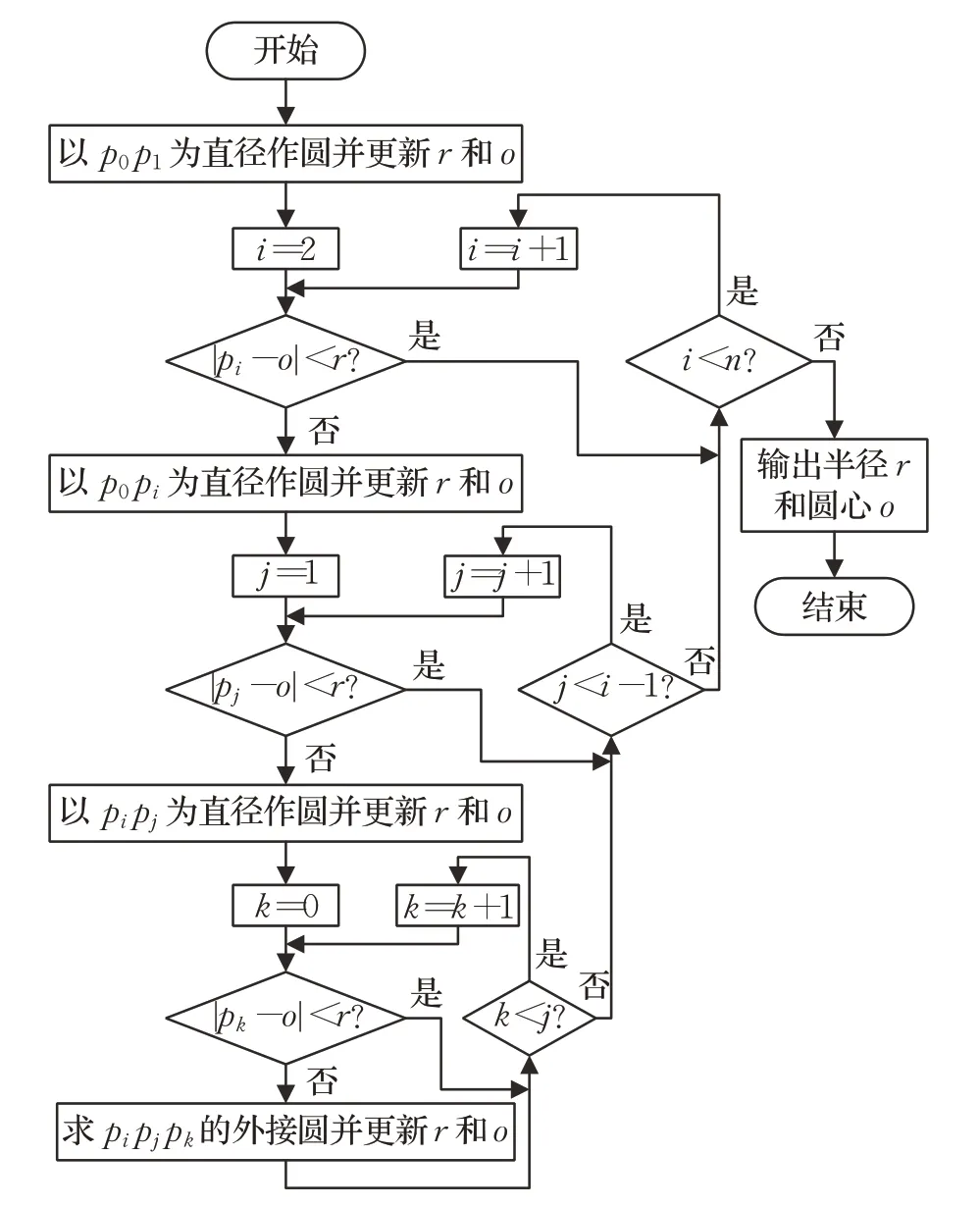
圖3 隨機增量法求最小外接圓流程圖Fig.3 Flow chart of obtaining minimum enclosed circle by randomized incremental algorithm

式中，p=(p x,p y);o=(o x,o y)。

如圖2所示，紅色標記為孔輪廓最小外接圓的圓心位置，根據縱坐標位置從大到小排列存儲，便于后續工件識別，孔特征圓心坐標如表1所示。

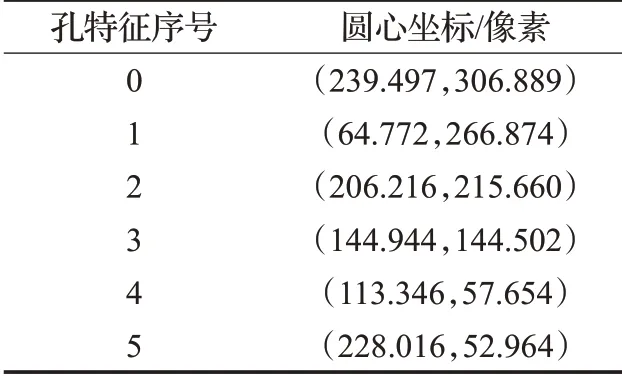
表1 圖2中孔特征圓心坐標表Table 1 Center coordinates of hole features in Fig.2

3 帶孔弱紋理堆疊工件識別

在提取工件孔特征的基礎上，首先采用改進幾何模板匹配算法進行工件識別，再根據孔特征之間是否存在邊緣剔除誤識別工件，從而實現對帶孔弱紋理工件的識別。

3.1 改進幾何模板匹配識別工件

傳統的幾何模板匹配是基于模板的顯著邊緣進行匹配，只適用于平面物體的檢測，當工件堆疊時工件發生傾斜時目標物與模板相差較大，導致傳統的幾何模板匹配識別效果不佳，且無法得到工件的6D位姿信息。本文所提出的改進幾何模板匹配算法是根據工件表面的加工特征（如：孔洞、槽等）之間的幾何約束進行工件識別，包括特征之間的距離約束和角度約束。在提取孔特征的基礎上，采用改進幾何模板匹配算法進行工件識別，實驗結果如圖4。

如圖4（a）和圖4（b）所示分別為工件在水平放置和30°傾斜放置時的模板工件特征圖，A、B、C、D分別為從上到下4個孔特征，可以看出真實工件滿足：與的約束條件，所以可根據孔特征之間的幾何約束進行工件識別：

圖4 工件識別階段實驗結果Fig.4 Experimental results of workpiece recognition stage

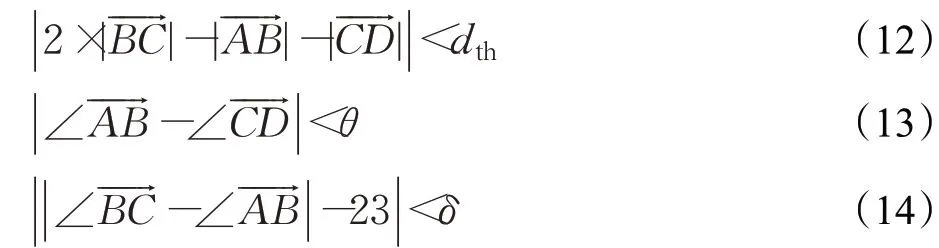
式中，dth為相同距離約束的閾值；θ為相同角度約束的閾值；δ為之間的角度約束閾值。由于在圖像采集、圓心計算過程會產生誤差，其距離、角度不完全相同，但誤差依然很小，因此取dth=8像素，θ=4°，δ=7°。

首先根據距離約束尋找工件上下兩個孔特征：

改進幾何模板匹配算法主要分為以下三個步驟：

步驟1已知各個孔特征的圓心坐標，根據式（5）尋找符合距離約束的上下兩孔特征。

步驟2提取步驟1中上下兩孔特征間的所有孔特征。

步驟3對步驟2中提取的孔特征根據式（12）~式（14）進行判斷，符合約束條件的孔特征與上下兩孔特征相組合，構成真實工件。

已知圖2的孔特征圓心坐標如表1所示，采用上述步驟進行工件識別，計算得到序號為0、2、3、4的孔特征滿足式（12）~式（15）的約束條件，構成真實工件，識別結果如圖4（c）所示。

由圖4（c）可知，本文所提出的改進幾何模板匹配算法可以有效地對上層帶孔弱紋理堆疊工件進行識別。

3.2 誤識別工件剔除

基于孔特征之間的幾何約束進行工件識別，在多工件識別時會出現不是同一工件的孔特征也滿足約束條件，從而導致誤識別情況發生，實驗結果如圖5，圖5（a）中存在誤識別的工件。由于真實工件的4個孔特征之間無其他邊緣，而誤識別的工件為跨工件識別，孔特征之間存在其他工件的邊緣（如圖5（a）黃色邊框所示），因此可以根據工件孔特征之間是否存在其他邊緣信息，對已識別的工件進行判斷，從而將誤檢的工件剔除，結合邊緣信息對圖5（a）進行判斷識別結果如圖5（b）所示。由圖5（b）可知，結合邊緣信息對已識別的工件進行判斷，可以將圖5（a）中誤識別的工件剔除，從而降低工件的誤檢率。

4 實驗與結果分析

為了定量評價工件的識別結果，使用查全率（Recall）和誤檢率（false positive rate，FPR）作為評價指標[16]，其計算公式為：

式中，REC為查全率；FPR為誤檢率；TP為工件被正確識別的個數；FN為工件未被正確識別的個數；FP為誤識別工件的個數；TOTAL為應該被識別工件的個數。

為了驗證本文提出的以工件表面孔洞為特征的改進幾何模板匹配算法的有效性，對合頁在任意旋轉、堆疊情況下進行實驗，采集堆疊圖像200張進行工件識別實驗，實驗環境為CPU Intel Core i5-8250U，基于Visual Studio 2017和OpenCV 3.2進行實驗。首先對所采集圖像中應該被識別工件的約束閾值進行統計，統計結果表明，dth的最大值為7.2像素，θ的最大值為2.7°，δ的最大值為6.0°，綜合考慮工件識別的容錯率以及運行時間，取dth=8像素，θ=4°，δ=7°。采用上述約束閾值在不同約束條件下進行工件識別實驗，統計結果如表2所示。

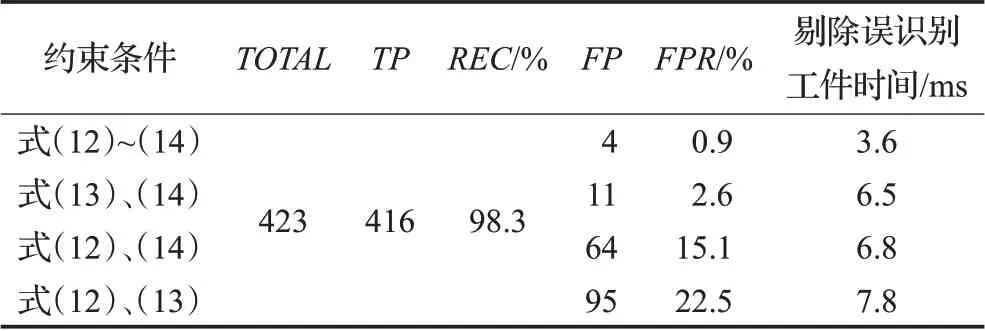
表2 不同約束條件下合頁識別統計結果Table 2 Statistical results of hinges recognition with different constraints

由表2可知，約束條件不會對真實工件產生影響，只是加速對誤識別工件的剔除，因此當減少約束條件時，并不會對識別的查全率產生影響。分別減少式（12）~（14）的約束條件時，工件的誤識別率以及剔除誤識別工件的時間相較于3個約束條件時明顯增加。其中，式（12）的約束條件對誤識別率的影響最大，因此本文選擇3個約束條件進行工件識別，以降低工件的誤檢率，工件識別查全率為98.3%，誤檢率為0.9%。

工件的部分識別結果如圖6所示，圖6所識別工件的信息如表3所示，圖6工件識別中每個步驟的運行時間如表4所示。

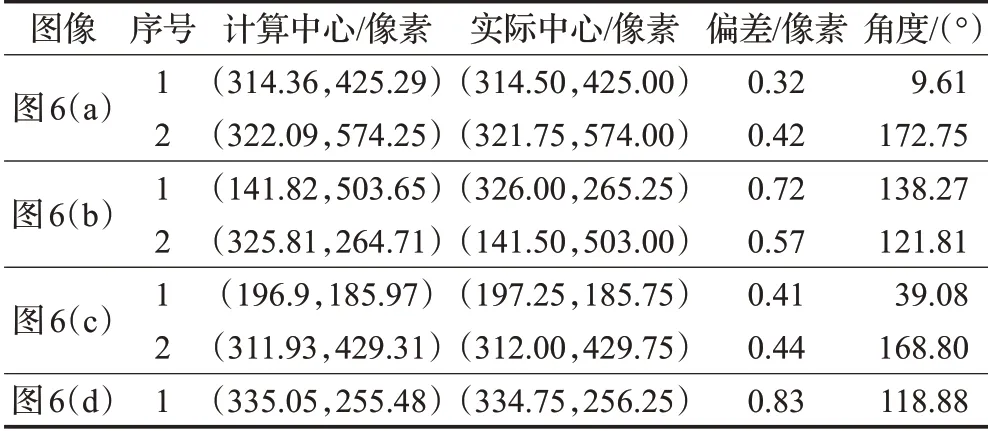
表3 圖6中工件識別結果信息表Table 3 Information of workpieces recognition results in Fig.6

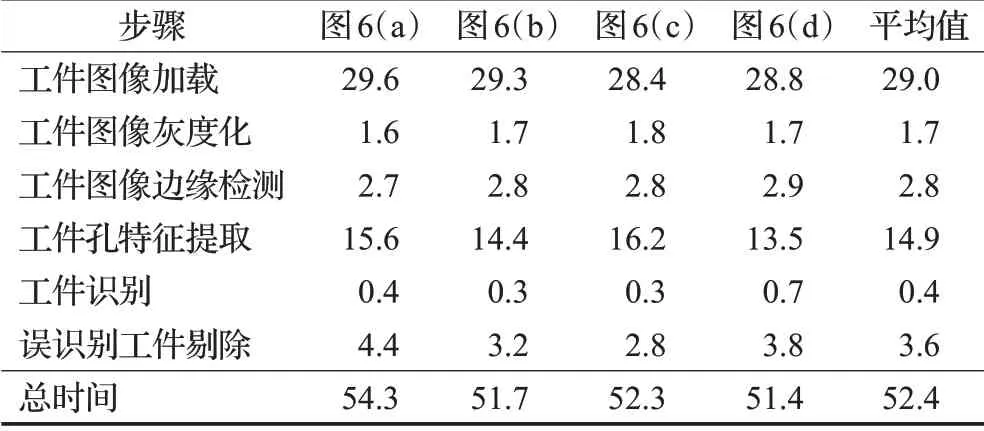
表4 圖6中工件識別運行時間表Table 4 Running time of workpieces recognition in Fig.6ms

圖6 部分工件識別結果Fig.6 Partial workpieces recognition results

由圖6可知，本文所提出的改進幾何模板匹配算法可以有效地對上層的帶孔弱紋理堆疊工件進行識別，當上層工件被分揀后再進行工件識別，循環完成對工件的識別和分揀。所提出的改進幾何模板匹配算法是基于工件的孔洞進行識別，工件的正確識別依賴于幾何特征的準確檢測，所以需要良好的光照條件易于孔洞與工件表面產生明顯的亮度差，便于工件孔輪廓提取，以提高工件識別的查全率和降低工件識別的誤檢率。

由表3可知，工件識別的平均偏差為0.63像素，而工件在圖像中長度為290像素，實際長度為115 mm，因此工件識別的平均偏差約為0.25 mm，滿足實際工件抓取的精度要求。

由表4可知，工件識別平均運行時間為52.4 ms，滿足實際工件抓取的速度要求，在圖像處理過程中，除加載圖像外，最耗時的步驟是工件孔特征提取。

5 結束語

本文對帶孔弱紋理堆疊工件的識別進行研究，提出了改進幾何模板匹配算法對具有孔洞特征的工件進行識別，有效解決了傳統工件識別方法中工件的平移、旋轉和堆疊對識別結果干擾的問題。在后續的研究中，（1）由于工件孔特征提取耗時較長，可以先對每個輪廓進行預判斷，包括尺寸、面積等，從而將明顯不符合孔輪廓特征的輪廓剔除，減少計算量，提高運行速度；（2）還需解決由于光照不均勻而引起的誤檢和漏檢情況，進一步提升算法的魯棒性。由于已經得到工件孔特征的圓心坐標，再基于EPnP（efficient perspective-n-point）算法并結合目標工件孔洞實際的幾何尺寸，可以得到工件的精準6D位姿信息，進行坐標變換后可引導機器人對工件進行分揀。