一種沉井潛入式豎井掘進機結構設計與研究

徐光億， 肖 威， 趙 飛， 齊志沖， 呂 旦， 趙子輝

(中鐵工程裝備集團有限公司， 河南 鄭州 450016)

0 引言

城市地下空間的開發利用已成為當今世界發展的趨勢，并成為衡量城市現代化的重要標志。隨著城市化的快速發展，城市可用面積越來越少。因此，開發和利用地下空間資源，修建與城市發展相適應的地下停車場、市政給排水管網、地下倉儲等基礎設施，對城市的建設與發展具有重要意義[1]。因此對應的施工裝備——豎井掘進機應運而生。

在豎井掘進機的發展過程中，已有學者對其施工工藝、掘進裝備未來發展、設備研究等方面進行了探索研究。劉志強等[2]對千米級豎井全斷面科學鉆進裝備與關鍵技術進行了分析與研究。賈連輝等[3]提出全斷面豎井掘進機上排渣技術，并對其關鍵技術進行了研究與試驗。王鵬越[4]和楊仁樹等[5]結合立井鑿井技術及施工裝備的歷史發展，對豎井掘進裝備的發展進行了探討。劉志強[6]和荊國業等[7]分別介紹了利用導孔排渣的機械破巖豎井掘進機鑿井工藝，并對掘進裝備進行了論述。現有的研究多集中在設備的施工工藝、未來發展等方面，而關于設備本身的研究相對較少。

本文基于工業試驗研發了一種新型豎井裝備——沉井潛入式豎井掘進機，介紹了設備的應用工況、結構組成與工作原理；分析了設備工作裝置受力特性，并對其進行了運動學分析；基于有限元分析方法和虛擬樣機技術，對關鍵結構件進行了強度分析和動態仿真模擬。

1 依托試驗項目

本項目依托于廠內工業試驗模擬現場工況。為更真實的模擬豎井掘進機的工況，建立了試驗臺進行開挖試驗。試驗項目可以模擬真實現場豎井施工情況。試驗采用基坑(井)內組裝始發，為減小豎井深度，降低豎井建造難度，豎井試驗臺設計為地面始發，利用組裝工裝作為設備始發鋼結構，進行設備始發掘進。基坑尺寸為上部直徑7.95 m，深6 m，可以供掘進機進行開挖試驗。圖1為試驗基坑(井)和設備始發現場照片。

樣機工業性試驗開挖介質為C30混凝土，開挖深度為0.5 m，試驗切削效率約為30 m3/h。采用抓斗形式出渣，出渣效率約為40 m3/h。該豎井掘進機較好地完成了工業試驗，成井精度控制在1‰以內，達到了預期效果。

(a) 試驗基坑(井)

(b) 試驗整機組裝

2 結構組成及工作原理

沉井潛入式豎井掘進機是結合沉井工法的一種新型豎井掘進機，主要應用于城市給排水豎井設施建設，地下停車場、倉儲設施建設，盾構始發井建設等領域，該設備是具有高安全性、集成化、機械化等特點的一種新型豎井施工設備。

沉井潛入式豎井掘進機由動力系統、開挖系統、推進系統、出渣系統、管片拼裝系統、控制系統、糾偏系統等組成。主機結構主要由支撐裝置、驅動裝置、回轉裝置、伸縮油缸、工作臂、截割臂、截割滾筒等組成。

動力系統包括2部分： 1)由馬達提供開挖裝置的回轉運動； 2)由截割臂上的電機提供截割滾筒旋轉運動。

開挖系統創新性采用縱軸結構的截割滾筒設計，主要由截割破巖(土)滾筒、截割電機及其他輔助零部件等組成，工作原理是截割電機驅動截割滾筒旋轉進行截割破巖工作。

其開挖軌跡從以下方面進行分析。

1)沿掘進方向的開挖軌跡分析。在截割滾筒開挖的過程中分為截割運動和進給運動，分別如圖2和圖3所示。其截割滾筒繞自身軸旋轉的同時也在沿截割臂軸線方向推進，因此截割滾筒的運動軌跡為圓弧螺旋線，如圖4所示。

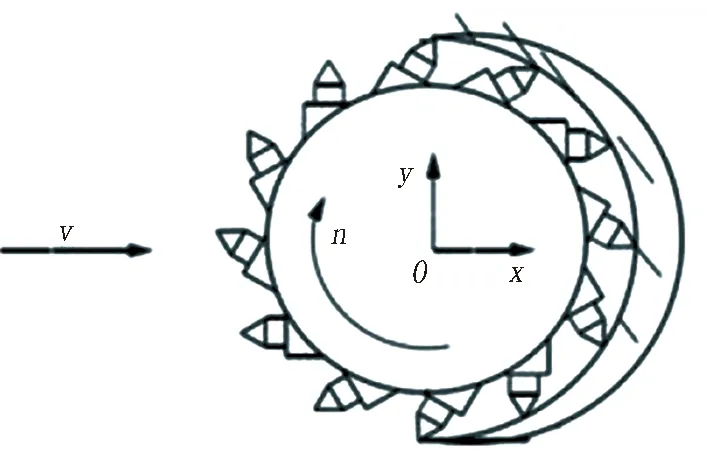
v為速度； n為轉速。下同。

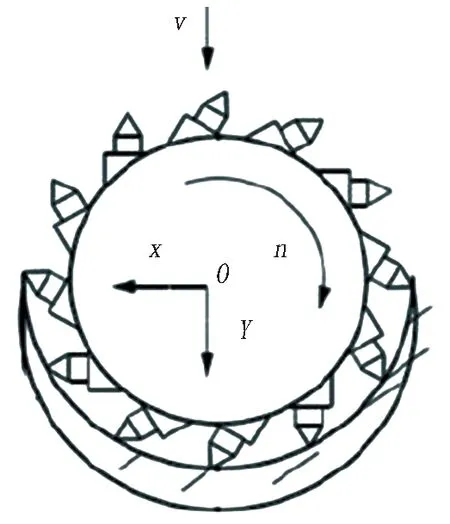
圖3 進給運動示意圖

圖4 圓弧螺旋線軌跡示意圖

2)沿圓周擺動方向的開挖軌跡分析。當沿圓周方向擺動時，同時伴隨著截割滾筒自身的旋轉，因此截割滾筒的運動軌跡為沿圓周方向的圓弧螺旋線，圖5為其中一段的圓周方向軌跡示意圖。

3)最終形成的開挖輪廓。通過截割滾筒自身的旋轉并通過伸縮油缸將其移動到某一基準位置進行定位，以定位基準位置依次向外進行回轉開挖，達到所需的開挖輪廓。以開挖直徑8 m為例，主機旋轉共7圈，主機旋轉依次向外進行開挖形成，開挖輪廓如圖6所示。

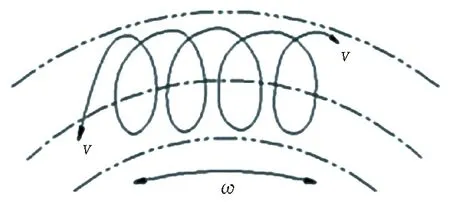
ω為角速度。

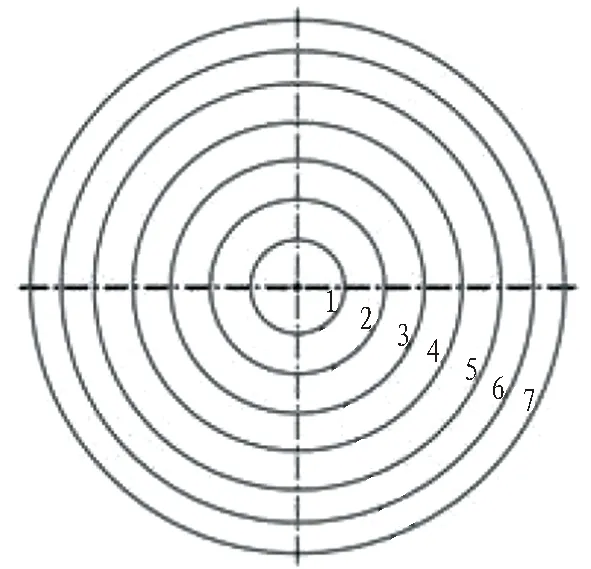
圖6 主機旋轉形成的開挖輪廓

推進系統基于滑箱軌道移動運動形式設計理念，創新性采用支腿與滑道形式來實現上下行程的移動。向下推進依靠推進油缸的伸出和預制管片的下沉來保證。

出渣系統可根據不同的地質條件采用不同的出渣方式。針對無水、少水地層，設備采用抓斗出渣的方式；針對富含地下水的工程采用泥漿出渣。

管節拼裝系統由龍門架、管節吊機、吊機軌道等組成；控制系統由液壓控制系統和電氣控制系統組成，利用其控制系統融合動態感知模擬技術來實現實時監測與控制；糾偏導向系統由糾偏導向儀和加壓裝置兩者協同進行控制。主機主要結構組成示意如圖7所示。

該沉井潛入式豎井掘進機結構小巧靈活，對地層及地面環境的擾動小，豎井斷面尺寸和形狀可變，遠程控制和操作，模塊化設計可根據需求進行靈活選配和定制。

3 掘進機的力學特性分析

沉井潛入式豎井掘進機在掘進過程中會伴隨著預制管片或現澆結構管片的拼裝來支撐井壁，設備的土壓力靠管片來承受，因此在計算掘進機的受力時，無需考慮來自井壁土壓力的作用，只需計算設備掘進過程中的受力即可。

在設備開挖過程中，工作裝置產生軸向進給力F軸向力、圓周回轉力F周向力、自身重力G1。設備受力示意如圖8所示，主要受到的力(考慮開挖位置在極限位置處)為截割滾筒壓力所產生的反力矩、截割滾筒軸向進給力引起的傾覆力矩[8]。

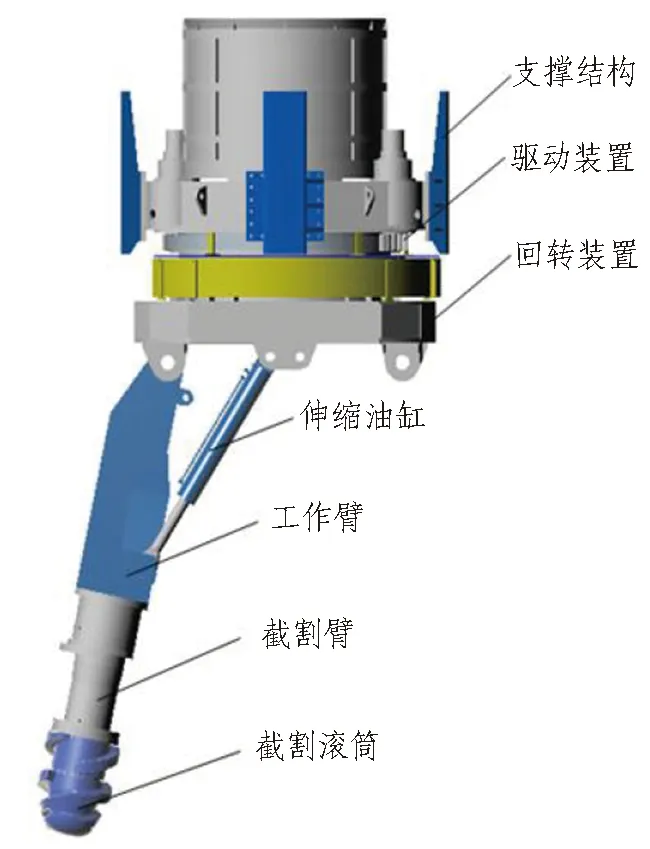
圖7 主機主要結構組成示意圖

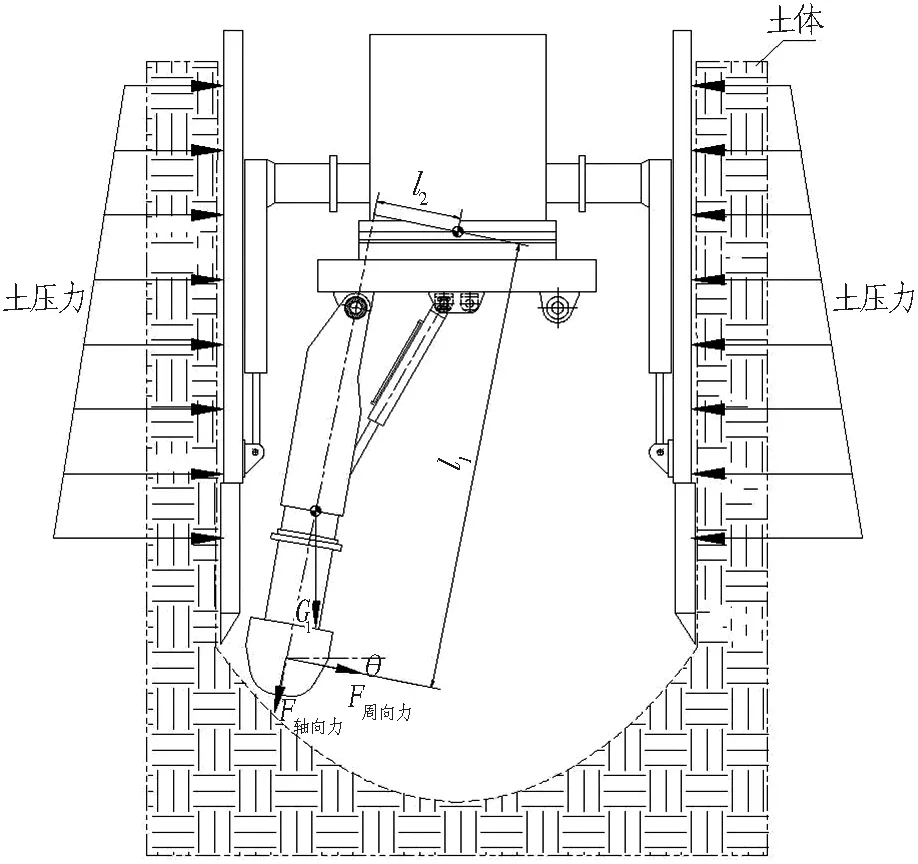
圖8 設備受力示意圖

截割滾筒壓力所產生的反力矩(逆時針方向)

M1=F周向力×l。

(1)

截割滾筒軸向進給力引起的傾覆力矩

M2=F軸向力×l。

(2)

中部回轉裝置受到的軸向力

F1=G1+F周向力×sinθ。

(3)

式(1)—(3)中：M1為截割滾筒壓力所產生的反力矩；M2為截割滾筒軸向進給力引起的傾覆力矩；G1為設備自身重力；F1為回轉支承受到的軸向力；θ為F周向力與水平方向的夾角；L為開挖裝置與設備重心位置的直線距離。

4 工作裝置的運動學模型構建與分析

根據掘進機實際工作過程中工作裝置的運動狀態，建立其工作裝置的運動簡化模型，如圖9所示。 伸縮油缸活塞桿的伸出和收回會引起工作臂空間轉角的變化。OA為固定臂，OB為轉動臂，BC為截割頭部，v1為油缸伸縮的速度方向，v2為設備掘進速度方向。

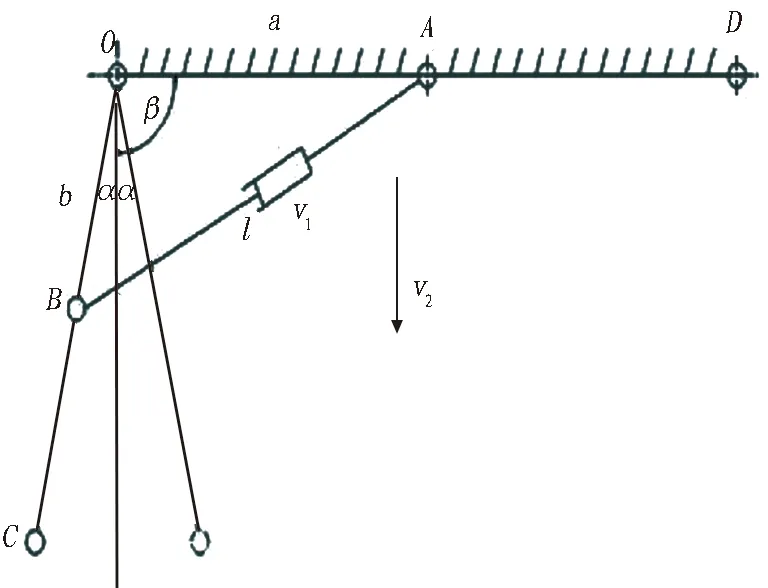
θ為轉動臂OB與固定臂OA的夾角，(°)； α為轉動臂OB與前進速度的夾角，(°)； a為固定臂OA的長度，mm； b為轉動臂OB的長度，mm； l為液壓缸伸出的長度，mm; 下同。

由圖9，可得：

(4)

θmin=αmin+β(β=90°) 。

(5)

(6)

(7)

(8)

以O點豎直向下位置為界線，以當前位置OB轉動臂依靠油缸收縮向中間豎直位置擺動的工況可得：

(9)

以O點豎直向下位置為界線，以當前位置OB轉動臂依靠油缸收縮從中間豎直位置向右側擺動的工況可得：

(10)

以截割臂為研究對象，通過截割臂中心點的位置坐標[x,y]以及截割臂的姿態角α可以確定截割臂的空間狀態，用矢量[xyα]T表示。

1)以當前OB截割臂的活動范圍在X軸豎直位置的左側范圍擺動的工況1進行分析。

在設備掘進的過程中，為了便于研究，假設液壓缸活塞桿直線往復運動速度和下沉掘進速度是恒定的，分別為v1和v2。將大地視為定坐標系XOY，將該機構視為動坐標系(以轉動點O為坐標原點，掘進方向為X軸，與掘進方向垂直的方向為Y軸)，如圖10所示。

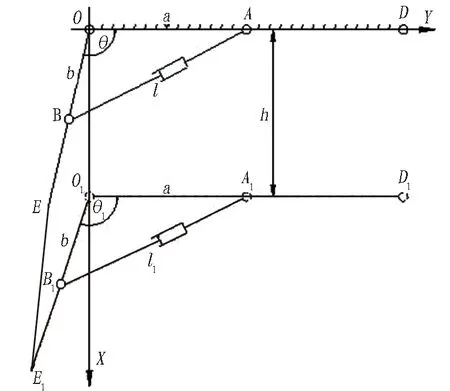
圖10 運動工況1空間姿態簡圖

截割臂參考點的位移矢量為EE1，參考點位置E1坐標可以表示為：

(11)

式中：h1表示掘進機向下掘進的深度，mm；c表示截割滾筒參考點E到轉動點O的距離，mm；θ1表示該空間任意狀態下工作臂OB與固定臂OA的夾角。

截割臂在伸縮油缸伸出階段的姿態空間狀態可以表示為：

EE1[]T=[x1y1α1]T

=[h1+c·sinθ1-c·cosθ1θ1-β]T。

(12)

同理，截割臂在油缸伸出階段狀態的基礎上繼續向下掘進深度h2，油缸保持狀態下的姿態空間狀態可以表示為：

E1E2[]T=[x2y2α2]T

=[h1+h2+c·sinθ2-c·cosθ2θ2-β]T。

(13)

同理，截割臂在油缸保持狀態下的基礎上繼續向下掘進深度h3，油缸收回狀態下的姿態空間狀態可以表示為：

E2E3[]T=[x3y3α3]T

=[h1+h2+h3+c·sinθ3-c·cosθ3θ3-β]T。

(14)

2)以當前OB截割臂在X軸正中豎直位置向下掘進的工況2進行分析，如圖11所示。

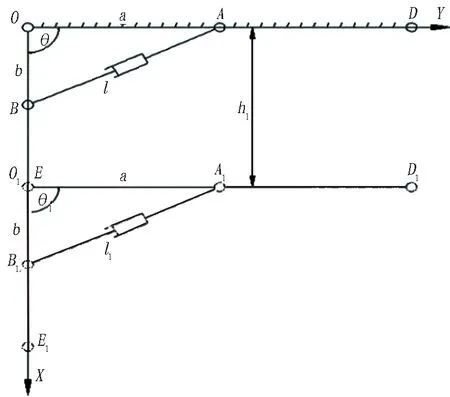
圖11 運動工況2空間姿態簡圖

截割臂姿態空間狀態可以表示為：

EE1[]T=[x1y1α1]T=[h1+c0β]T。

(15)

3)以當前OB截割臂的活動范圍在X軸豎直位置的右側范圍擺動的工況3進行分析，如圖12所示。

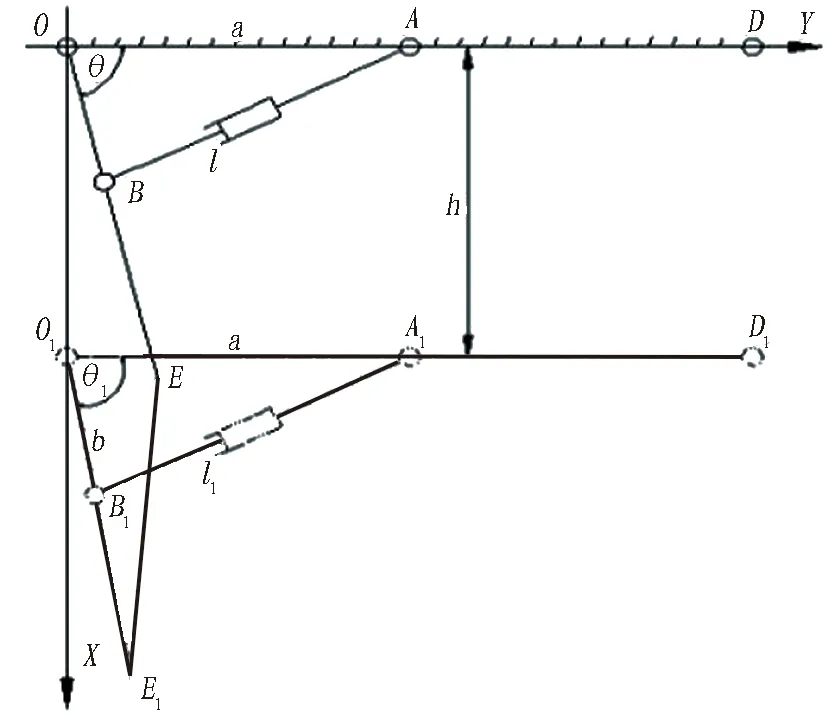
圖12 運動工況3空間姿態簡圖

(16)

截割臂在油缸伸出階段的姿態空間狀態可以表示為：

EE1[]T=[x1y1α1]T=[h1+c·sinθ1c·cosθ1β-θ1]T。

(17)

同理，截割臂在油缸伸出階段狀態的基礎上繼續向下掘進深度h2，油缸保持狀態下的姿態空間狀態可以表示為：

E1E2[]T=[x2y2α2]T

=[h1+h2+c·sinθ2c·cosθ2β-θ2]T。

(18)

同理，截割臂在油缸保持狀態下的基礎上繼續向下掘進深度h3，截割臂在油缸收回狀態下的姿態空間狀態可以表示為：

E2E3[]T=[x3y3α3]T

=[h1+h2+h3+c·sinθ3c·cosθ3β-θ3]T。

(19)

5 設備關鍵部件的有限元分析

5.1 工作臂有限元分析

工作臂作為整機主要的運動與支撐零部件，是連接回轉運動以及截割滾筒的關鍵結構，在實際工作過程中工作臂的受力情況對于整機的可靠性至關重要，因此需要對其進行強度分析。

5.1.1 有限元模型的建立

在不影響精度的前提下，建立計算模型時，應簡化模型結構，以提高運算速度。為此，對模型進行幾何修改，將模型上的非倒角結構和圓角以直角代替，然后進行網格劃分[9-10]。采用有限元法對工作臂三維模型進行網格劃分，如圖13所示。采用四面體網格，劃分網格單元數量95 594，節點數量177 080。采用四面體結構單元和線彈性材料模型，在網格劃分前先賦予結構材料屬性，定義材料的彈性模量為206×103MPa，泊松比為0.3。

5.1.2 材料的設置與參數

結構采用Q345B焊接而成，其材料參數見表1。

5.1.3 載荷與邊界條件

根據受力情況，在上部連接位置處與側部伸縮油缸連接固定位置處施加固定約束，與下部截割臂連接端面的位置施加600 kN·m的力矩，并添加重力約束。工作臂施加邊界條件如圖14所示。

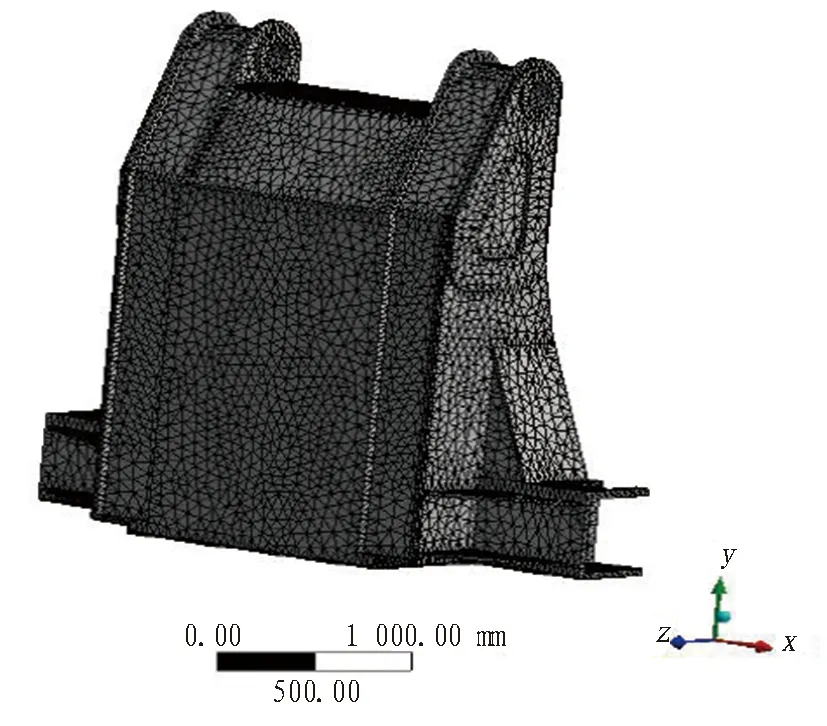
圖13 工作臂三維模型網格劃分

表1 材料參數表

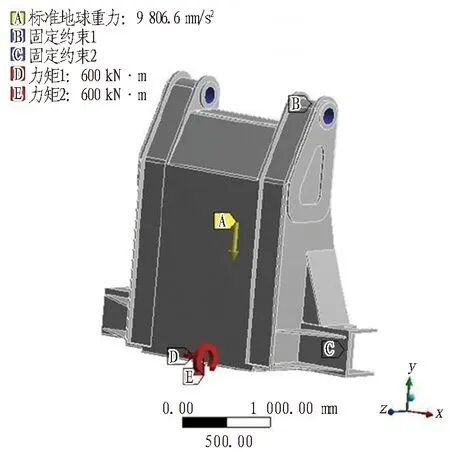
圖14 工作臂邊界條件

5.1.4 應力分析

圖15為工作臂應力云圖。從圖15分析結果可知，工作臂大部分區域的應力在150 MPa以下，局部會由于三維模型繪制的結構尖角以及尖角過渡處出現應力集中導致應力值變大。在由于計算簡化引起的應力值變大的位置，可以采用較大直徑圓角過渡處理，這樣可大大降低這些位置的應力值[9]。因此工作臂結構整體受力狀況較好，滿足設計要求。

圖15 工作臂應力云圖(單位： MPa)

5.2 回轉裝置有限元分析

回轉裝置是回轉運動的關鍵結構件，回轉裝置是連接驅動裝置與開挖裝置的載體，其受力情況相對較差，因此需要對其進行強度分析。

5.2.1 有限元模型的建立

網格劃分如圖16所示，采用四面體網格，劃分網格單元數量95 594，節點數量177 080。采用四面體結構單元和線彈性材料模型，在網格劃分前先賦予結構材料屬性，定義材料的彈性模量為206×103MPa，泊松比為0.3。

圖16 回轉裝置三維模型網格劃分

5.2.2 載荷與邊界條件

回轉裝置約束與加載情況如圖17所示。在上部法蘭連接端面位置處做固定約束處理；在底部端面及圓周面處施加回轉力矩和傾覆力矩；施加斜向力；添加重力。

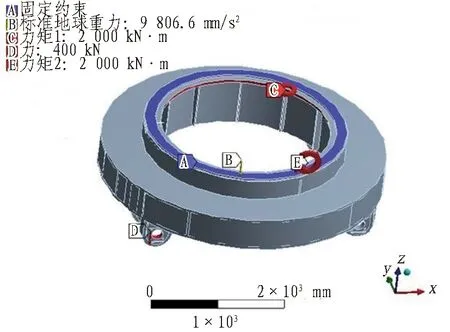
圖17 回轉裝置約束與加載情況

5.2.3 應力分析

圖18為回轉裝置應力云圖。從圖18分析結果可知： 回轉裝置的應力在110 MPa以下，結構的整體受力狀況較好，滿足設計要求。

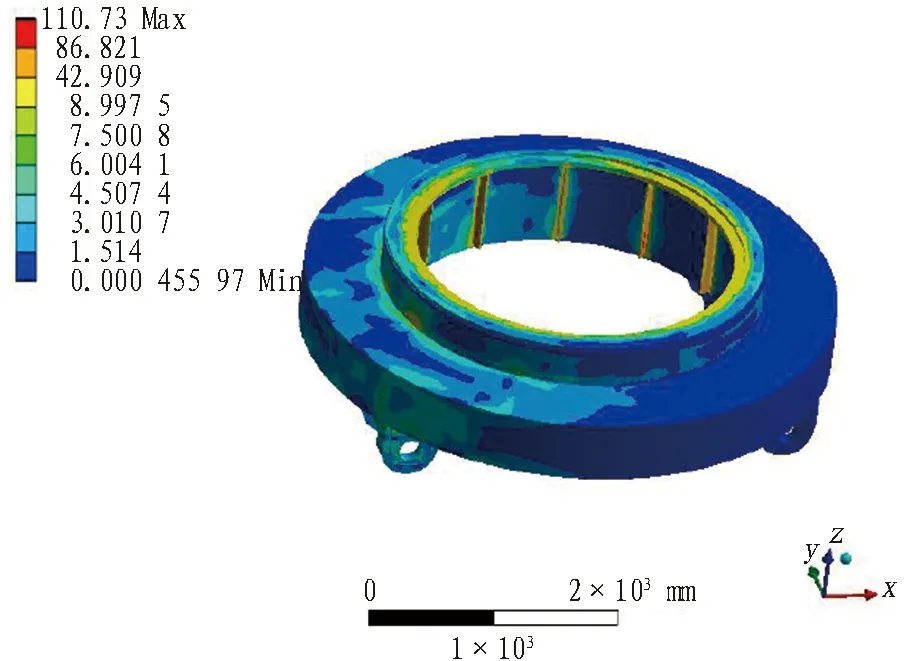
圖18 回轉裝置應力云圖(單位： MPa)

6 工作裝置運動學及動力學分析

對工作裝置進行三維建模并簡化，然后把模型導入仿真軟件中建立虛擬樣機模型，并進行模型定義與各種約束、驅動和力的添加，具體包括以下部件的定義： 2個球鉸副、5個旋轉副、2個移動副、5個固定副、1 個齒輪副、2個液壓缸驅動、1個回轉驅動和1個結構重力[11-13]。

工作裝置的運動形式有2種： 1)上部驅動帶動回轉裝置進行工作裝置的回轉運動； 2)伸縮油缸的伸縮帶動工作臂及截割滾筒的擺動運動。

6.1 回轉運動

以回轉裝置旋轉為主，設置時間為35 s，設其驅動函數為：

STEP(time,0, 0, 5, 190 d)+STEP(time, 5, 0, 15, -190 d)+STEP(time, 15, 0, 25, -190 d)+STEP(time, 25, 0, 35, 190 d)，根據函數設置進行仿真分析。

回轉運動與工作臂質心運動曲線如圖19所示。可以看出在0～5 s其速度曲線波動較大，其余時間運動相對平穩。整個位移曲線呈現規律性的變化，符合實際運動情況。

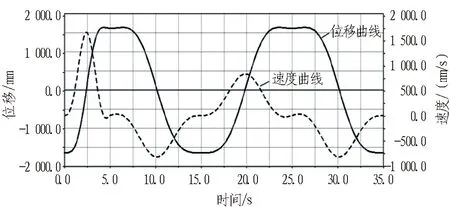
圖19 回轉運動與工作臂質心運動曲線

工作臂與回轉裝置連接處的受力曲線如圖20所示，可以看出其受力曲線呈現規律性變化，0～15 s為1個周期循環變化，其受力最大值為300 kN。

圖20 工作臂與回轉裝置連接處受力曲線

6.2 擺動運動

以伸縮油缸伸縮為主，設置時間為80 s，設其驅動函數為：

STEP(time, 0, 0, 10, 500)+STEP(time, 10, 0, 20, -500)+STEP(time, 20, 0, 30, -500)+STEP(time,30,0,40, 500)

擺動運動與工作臂質心運動曲線如圖21所示，可以看出其位移曲線隨著油缸的伸縮運動呈現規律性變化；其速度曲線在油缸伸出與收縮的轉換點出現尖峰，其余時間速度相對平穩。

工作臂與回轉裝置連接處的受力曲線如圖22所示，可以看出其受力曲線呈現規律性變化，最大值為580 kN，最小值為220 kN。

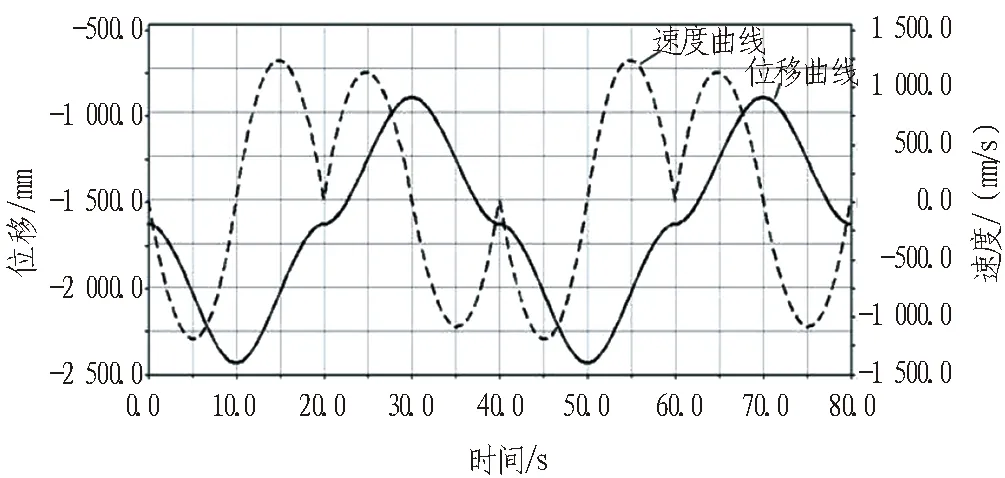
圖21 擺動運動與工作臂質心運動曲線

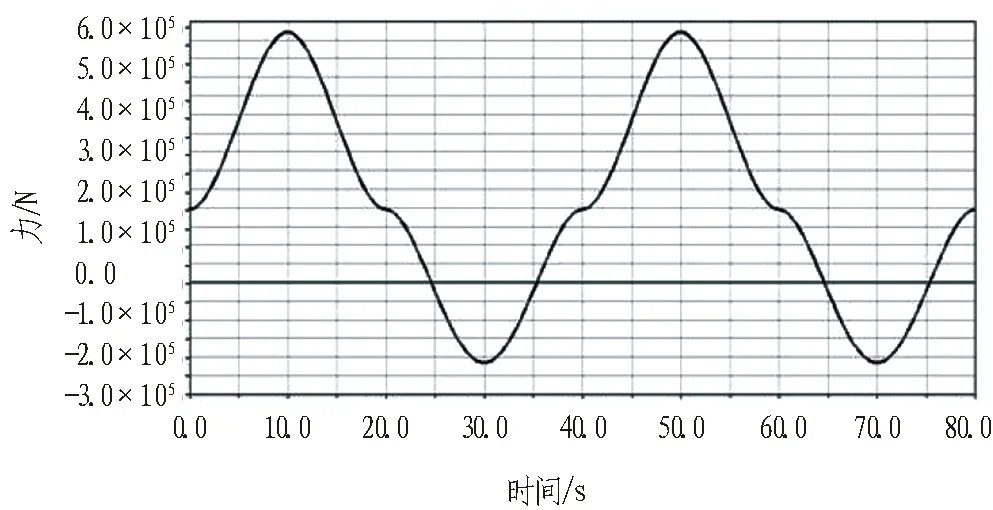
圖22 工作臂與回轉裝置連接處受力曲線

7 結論與討論

本文建立了沉井潛入式豎井掘進機的力學模型，基于力學模型對掘進機的回轉裝置、工作臂進行靜強度分析，驗證了其在強度和剛度方面設計的合理性。以工作裝置為研究對象，基于運動學模型對工作裝置進行了運動學理論分析。基于虛擬樣機技術，在回轉運動和擺動運動2種運動形式下，對其工作臂以及連接位置處進行了運動學研究和動力學研究。

在設備掘進過程中，整機的自動化作業可大大提高施工效率，整機的輕量化設計、安裝與吊裝作業的方便快捷也可大大提高作業效率，從而降低設備制造以及施工成本。因此，整機零部件的輕量化設計研究以及結構設計的自動化程度可作為接下來的探索方向。