基于饋源固定的雙頻掃描反射陣設計

張 瑩，左 樂，李 洋，何清明

(電子信息控制重點實驗室，四川 成都 610036)

0 引言

自20世紀末電磁超材料出現以來，其獨特的電磁性能為工程電磁學尤其是天線技術提供了廣闊的可能性和自由度[1-4]。對于在雷達、制導、電子戰和通信系統中廣泛應用的高增益天線，傳統的反射面天線由于利用反射反向的金屬材料，僅能通過幾何形狀來實現相位補償，因此反射面為非平面的拋物面，剖面高度較高。基于超材料技術的平面反射陣，利用超材料反射系數可設計的原理，采用不同反射相位的散射體代替傳統金屬，結合了陣列天線和反射面天線的優點，具有剖面低、結構簡單和易集成等特點。反射陣通過調節入射場相位實現對輻射場的控制，由多個超材料反射單元組成，每個反射單元提供一個相位補償量，使饋源發射的電磁波在反射陣單元所在平面形成等相，從而產生高增益、窄波束輻射[5-6]。

由于高增益天線的波束寬度較窄，為實現更寬空域的波束覆蓋，反射陣天線需具備掃描性能。且伴隨著衛星通信技術的發展，針對1.575 GHz的GPS頻段及2.4 GHz的藍牙、WiFi頻段的雙頻掃描反射陣需求日益突出。文獻[7]總結了反射陣天線的掃描方法，常見實現反射陣波束掃描的技術手段主要分為2類：第1類通過移動饋源以實現波束掃描[8-10]，這類方法對于饋源設備量大、難以移動場景無法應用；第2類通過獨立調節反射陣單元相位，以達到波束掃描的目的[11- 16]，典型的調節方式為電控形式的PIN管、FET管或可變電容等，這類方法由于控制參數較多，導致設計復雜度提升，且結構復雜、可靠性低、價格昂貴，同時由于加入大量的有源器件，使其損耗較大，影響反射陣天線效率。文獻[17]設計了一種旋轉反射面實現波束掃描的反射陣，但只進行了單頻設計，且未對掃描原理進行闡述。相對于單頻反射陣，雙頻反射陣波束掃描的設計難度更大。由于雙頻在掃描時所需的相位變量不同，若獨立調節反射陣單元相位，則控制變量多而繁雜，系統復雜度急劇上升。

本文通過旋轉反射陣面實現了雙頻波束掃描，僅一個控制參數即可實現雙頻波束掃描，具有系統復雜度低、可靠性高、易安裝和損耗低等優點。通過對旋轉前后反射陣口面相位分布的理論分析，結合陣列天線理論，推導出波束掃描角與陣面旋轉角的解析關系。對解析表達式的進一步分析表明，形成的相位分布具備寬帶特性，即通過旋轉反射陣陣面實現波束掃描的方法是一種寬帶方法，既可以應用在寬帶掃描反射陣中，又可以應用在多頻或雙頻反射陣中。隨后采用反射陣陣列理論[18]對本文提出的掃描方法進行驗證。利用25×25單元的雙頻掃描反射陣進行設計驗證，并在1.575，2.4 GHz頻段獲得了良好的掃描特性。

1 理論推導

本文提及的反射陣結構及坐標示意如圖1所示，這里假設饋源的波束指向為反射陣面中心位置，且反射陣面與xoy面的初始偏饋角為θ0。

圖1 掃描反射陣結構示意

反射陣天線通過反射陣單元的相位補償，實現理想的輻射特性。反射陣天線的補償相位公式為：

Φr=-Φ1+Φb=kRi+Φb,

(1)

其補償相位包含兩部分，第一部分Φ1為由饋源到反射陣單元的相位延遲；k為空氣中的傳播常數；Ri為反射陣單元到饋源的空間距離；Φb為實現波束指向的相位分布。此時，饋源到反射陣面不同位置的相位延遲為：

Φ1=-k[x2+(lcosθ0)2+(f-lsinθ0)2]1/2,

(2)

式中，f為焦距；x和l分別為反射陣單元在x，y軸的坐標值。

根據陣列天線理論[5]，波束指向θb方向時的陣列單元相位分布滿足：

Φb=klsin(θb-θ0)+Φ0,

(3)

式中，Φ0為固有相位，為一常數。

根據反射陣工作原理，反射陣單元的相位補償量為：

Φr=klsin(θb-θ0)+Φ0+

k[x2+(lcosθ0)2+(f-lsinθ0)2]1/2。

(4)

當反射陣面具備如上的補償相位時，由饋源發出的球面波經反射陣面后的相位分布為：

Φs1=klsin(θb-θ0)+Φ0。

(5)

由陣列天線理論可知，此時反射陣的最大輻射方向為θb。至此，反射陣面的相位分布已固化。當反射陣面繞x軸旋轉θs時，從饋源到反射陣面的相位延遲變為：

Φ2=-k[x2+(lcos(θ0+θs))2+(f-lsin(θ0+θs))2]1/2。

(6)

此時，由饋源發出的球面波經反射陣面后的相位分布為：

Φs2=klsin(θb-θ0)+Φ0+

k[x2+(lcosθ0)2+(f-lsinθ0)2]1/2-

k[x2+(lcos(θ0+θs))2+(f-lsin(θ0+θs))2]1/2。

(7)

當θ0較小，將式(2)進行二階泰勒展開，近似為：

(8)

(9)

式中，ri為每一個反射陣單元距離坐標原點，即反射面中心的距離。由此可見，此擾動系數與反射陣單元位置、焦徑比和反射面旋轉角度有關。在反射陣中心位置ri=0，擾動系數Wi=1，隨著單元遠離中心區域呈現下降趨勢，邊緣處最小。對于邊緣處單元，ri≈D/2，D為反射陣口徑尺寸，因此邊緣單元的擾動系數與焦徑比呈正比，焦徑比越大，擾動系數越接近于1。以反射陣單元中間一列為例，圖2給出了當θs=15°時，不同焦徑比條件下各單元對應的擾動系數變化曲線。分析曲線可以看出，焦徑比越大，全空域范圍內擾動系數越接近于1。同時由于反射陣單元幅度從中心向邊緣遞減，因此對合成波束指向起主要作用的單元集中在中心區域。由圖2可以看出，當焦徑比大于0.7時，中間區域單元的擾動系數近似為1。綜上所述，對于長焦反射陣，為了分析方便，可將此擾動系數近似為1，即：

圖2 不同焦徑比的擾動系數

Φs2?klsin(θb-θ0)+Φ0+klsinθs。

(10)

當θb及θ0較小時，根據三角函數的和差化積及半角公式，又可做如下近似：

Φs2?klsin(θb-θ0+θs)+Φ0。

(11)

由式(11)可見，當反射陣面繞x軸旋轉θs時，其波束指向也偏轉了θs。同時應當注意，根據陣列天線理論，此波束偏轉是相對于反射陣面法線方向，而由于反射陣面相對于xoy面已經旋轉了θs，因此相對于xoy面，波束共偏轉了2θs。可以推算出，在保持反射陣饋源不動的情況下，僅旋轉反射陣面可以實現反射陣的波束掃描，且反射陣旋轉θs，其波束指向近似偏轉了2θs，這說明反射陣面的旋轉范圍為波束掃描范圍的一半，波束掃描的速度是反射陣面旋轉速度的2倍。

根據陣列天線理論可知，隨著反射陣陣面旋轉其掃描波束在不同頻點的指向相同，即波束偏轉與頻率無關，因此通過旋轉反射陣陣面實現波束掃描的方法是一種寬帶方法。掃描方法的寬帶特性意味著其既可以應用在寬帶掃描反射陣中，又可以應用在多頻或雙頻反射陣中，掃描方法的寬帶特性是實現雙頻反射陣的必要條件。

2 方法驗證

本文提出了一種適用于雙頻平面反射陣的波束掃描方法，并進行了理論推導。利用反射陣陣列理論[18]對上述掃描方法進行數值驗證，以論證此掃描方法與本文設計需求的符合性。

2.1 掃描驗證

首先，與上節推導假設一致，選取θb為較小值進行驗證。這里選取的反射陣焦徑比f/D為0.85，初始偏饋角θ0為15°，初始波束指向θb為0°。圖3(a)給出了初始波束指向θb為0°時反射陣方向圖隨旋轉角的變化情況。由此可知，隨著反射陣面的旋轉，其波束指向隨之偏轉，實現了反射陣的波束掃描。其次，反射陣旋轉10°，其波束指向偏轉了20°，反射陣旋轉20°，其波束偏轉了40°，即掃描波束偏轉量近似為反射陣面旋轉角度的2倍，與上節的推導一致。

其次，為了驗證此掃描方法的普適性，對θb非較小值情況進行驗證。圖3(b)給出了初始波束指向θb為30°時的情況。此時，當反射陣不旋轉時最大波束指向為30°。可見隨著反射陣面的旋轉，其波束指向依然隨之發生偏轉，證明此方法在θb非較小值時依然可實現波束掃描。當反射陣旋轉15°，波束指向約為60°；當反射陣旋轉-15°，其波束指向約為0°，即波束偏轉量仍然近似為反射陣面旋轉角度的2倍。可見，上節結論不僅適用于θb較小的情況，而是具有普適性。

(a) θb=0°

2.2 雙頻驗證

理論推導揭示了該方法具有寬帶特性，可應用于雙頻設計。本小節給出雙頻數值驗證。圖4(a)給出初始波束指向θb為30°，反射陣旋轉前雙頻的歸一化方向圖，圖4(b)給出反射陣旋轉-15°后，雙頻的歸一化方向圖。由此可見，隨著反射陣面的旋轉，雙頻的波束指向一同隨之發生偏轉，且旋轉前后雙頻的波束指向相同，驗證了本文提出的掃描方法可應用于雙頻掃描反射陣設計。

(a) 旋轉前

3 雙頻掃描反射陣設計

設計的雙頻掃描反射陣與上一小節參數保持一致，焦徑比f/D為0.85，初始角度θ0為15°，初始波束指向θb為30°。此雙頻反射陣包含了25×25單元，單元呈矩形周期分布，排布間距為60 mm，本文提出的波束掃描方法可適用于多種極化，為了簡便,此處采用垂直極化進行驗證。

單元設計如圖5所示，單元圖形印制于介電常數為2.55的印制板上，印制板厚度為2 mm，印制板距離金屬底板的高度為10 mm，單元周期為60 mm。印制圖形為4個寬度為1 mm的圓環，最外環外半徑為R1，與之相鄰的圓環外半徑為0.9×R1，通過改變R1的大小以控制低頻相位；第3個圓環外半徑為R2，最內環外半徑為0.8×R2，通過改變R2的大小以控制高頻相位。圖6(a)給出低頻相位隨R1變化曲線，圖6(b)給出高頻相位隨R2變化曲線，可以看出該單元在2個頻率相位變化范圍均超過360°，滿足雙頻設計要求，可用于雙頻反射陣設計。

圖5 反射陣單元示意

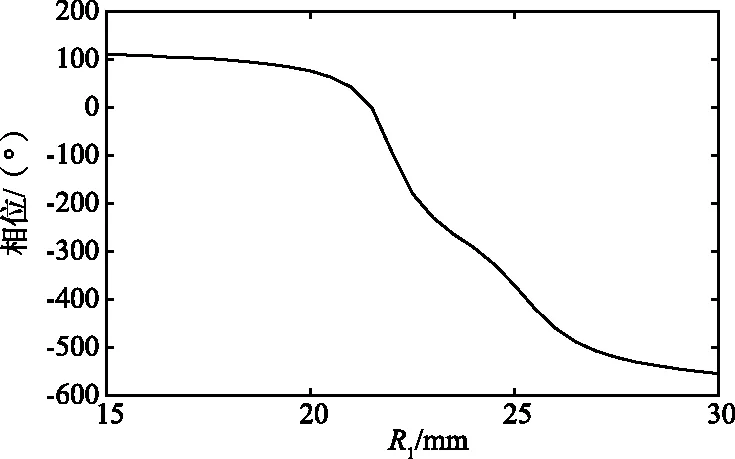
(a) 1.575 GHz

根據式(4)分別計算雙頻所需的補償相位，在不同位置根據圖6的相位隨尺寸變化曲線選取合適的參數，形成反射陣面如圖7所示。

圖7 反射陣面示意

利用全波算法進行仿真驗證，圖8給出掃描方向圖。當反射陣不旋轉時，天線雙頻波束指向均為30°，當反射陣旋轉15°，波束在雙頻均掃描至60°，當反射陣旋轉-15°，波束在雙頻均掃描至0°，即通過旋轉反射陣面實現了雙頻波束掃描，且雙頻的掃描波束指向相一致，與上節結論一致。

(a) 1.575 GHz

為進一步驗證此設計方法，加工實物進行測試驗證。圖9給出雙頻掃描反射陣實物照片。圖10和圖11給出實測結果與仿真結果的對比曲線，可見實測結果與仿真結果基本吻合，有效地驗證了本文設計方法的有效性。

圖9 雙頻掃描反射陣實物照片

(a) 0°

(a) 0°

根據第一節的理論推導，旋轉反射陣面相位變化具有連續性，可知掃描波束也具有連續性，其增益變化也具有連續性。表1給出典型掃描角度波束增益值，可以看出，該雙頻掃描反射陣在60°空域范圍內掃描波束增益下降小于2 dB，具有良好的雙頻掃描特性。

表1 波束增益值匯總

4 結束語

本文設計了一種基于饋源固定的雙頻掃描反射陣，定量對波束掃描方法進行了理論分析，并給出推導過程。通過分析可知該方法具有掃描速度快、寬帶等特性。利用此方法進行雙頻掃描反射陣設計，并通過25×25單元的雙頻掃描反射陣對此設計方法進行了驗證，最終在60°空域范圍內獲得了良好的雙頻掃描特性，有效地證明了本文設計方法適用于雙頻掃描反射陣的設計。

提出的波束掃描方法具有寬帶特性，可進一步基于此方法進行饋源固定的多頻及寬帶反射陣設計。