周期性多孔結構特征值拓撲優(yōu)化

付君健， 張 躍， 杜義賢， 高 亮

(1. 水電機械設備設計與維護湖北省重點實驗室， 湖北 宜昌 443002；2. 三峽大學 機械與動力學院， 湖北 宜昌 443002； 3. 華中科技大學 數(shù)字制造裝備與技術國家重點實驗室， 武漢 430074)

周期性多孔結構是功構一體化的優(yōu)良載體[1]，在航空航天、汽車、醫(yī)學植入等領域具有廣泛的應用前景。周期性多孔結構可設計性強，能根據(jù)功能特性需求，設計出不同形狀、尺寸和孔隙率的多孔構型。對于含有多孔結構的復雜機電系統(tǒng)，多孔結構的固有頻率要求遠離驅(qū)動系統(tǒng)的工作頻率。

在給定的材料屬性和邊界條件下，周期性多孔結構的固有頻率與拓撲構型相關，通過改變多孔結構的拓撲構型，可以被動地改變結構固有頻率，使其脫離工作環(huán)境下的激勵頻率，從而避免劇烈共振導致的結構失穩(wěn)和破壞。特征值拓撲優(yōu)化是改變多孔結構固有頻率的有效設計方法，與宏觀結構特征值拓撲優(yōu)化[2]的不同之處在于，周期性多孔結構通過改變局部單胞的幾何特征，實現(xiàn)整體結構特征值的優(yōu)化。

由于存在尺度跨越，特征值有限元求解方法對周期性多孔結構拓撲優(yōu)化有重要影響。對于具有相同自由度數(shù)量的結構系統(tǒng)，求解頻率和振型的特征值問題，其計算時間將比靜力分析高出一個數(shù)量級[3]。如果是局部幾何特征較多的多孔結構，計算量將更大。由于尺度小、特性多、計算量大，多孔結構宏觀等效屬性計算一般需采用模型縮減方法。均勻化法是常用的周期性多孔結構宏觀等效屬性計算方法[4]，主要用于計算宏觀等效彈性矩陣，等效彈性矩陣則用于計算等效剛度矩陣和等效質(zhì)量矩陣[5]。均勻化法的假設之一為尺度分離，即多孔微結構尺寸遠遠小于宏觀結構尺寸。在實際應用中，均勻化法更適合小尺度、大規(guī)模的周期性多孔結構分析與優(yōu)化。對于有尺度要求的多孔結構設計，需采用尺度關聯(lián)的模型縮減方法進行宏觀等效屬性計算，如子結構法[6]、尺度關聯(lián)均勻化法[7]、多尺度有限元法[8]，或者采用迭代法進行求解[9]。

子結構法作為一種較為成熟的模型縮減方法，近年來逐漸被用于細觀尺度周期性多孔結構的拓撲優(yōu)化[10]。子結構法具備尺度關聯(lián)的特性，適用于尺度關聯(lián)、中等規(guī)模多孔結構分析與優(yōu)化。目前，基于子結構法的多孔結構拓撲優(yōu)化研究主要集中于靜力學問題[11-12]，實現(xiàn)周期性和多層級多孔結構剛度拓撲優(yōu)化。雖然已有研究將子結構法用于多層級結構一階特征值拓撲優(yōu)化[13]，并取得了一定效果，但子結構靜態(tài)凝聚求解高階特征值會產(chǎn)生較大誤差。因為子結構靜態(tài)凝聚忽略了動力學方程中的慣性項，導致縮減的質(zhì)量矩陣為近似值，只有在頻率較低時才有較高的縮減精度，隨著頻率的增加，數(shù)值誤差將逐漸增大。O’Callahan[14]提出了針對動力學問題的改進縮減系統(tǒng)(improved reduced system, IRS)，保證了子結構法的動態(tài)縮減精度，但采用子結構法進行多孔結構特征值分析與優(yōu)化仍存在諸多問題有待探索，如集中質(zhì)量施加、特征值尺度問題、特征值拓撲優(yōu)化敏度分析等。

本文基于子結構動態(tài)凝聚方法，探討其動態(tài)縮減精度，建立了周期性多孔結構特征值最大化拓撲優(yōu)化模型，實現(xiàn)了尺度關聯(lián)的二維、三維周期性多孔結構的拓撲優(yōu)化，并揭示了細觀尺度多孔結構特征值拓撲優(yōu)化的尺度效應。

1 周期性多孔結構幾何與物理描述

1.1 周期性多孔結構幾何描述

針對周期性多孔結構幾何描述，提出局部水平集函數(shù)(local level set function, LLSF)的概念，即在全局設計域中定義多個局部水平集函數(shù)描述細觀尺度下的周期性多孔結構，將多孔結構幾何邊界隱式地嵌入高一維的函數(shù)。局部水平集函數(shù)使得多孔結構的幾何描述更加簡單，也使得多孔結構拓撲優(yōu)化具有更多的設計自由[15]。如圖1所示，將二維周期性結構設計域離散為M個細觀結構，在每個細觀結構內(nèi)部定義一個局部水平集函數(shù)，Φi表示其中一個細觀結構的水平集函數(shù)

(a) 零水平面

(1)

式中：下標i為設計域D內(nèi)的子結構編號；x為空間坐標向量；Ω為結構域；?Ω為結構邊界。

所有細觀結構水平集函數(shù)Φi(xi)的集合組成了全局水平集函數(shù)Φ(x)

(2)

局部水平集函數(shù)Φi在子結構內(nèi)部動態(tài)演化的Hamilton-Jacobi方程如下

(3)

式中：vn, i為局部水平集函數(shù)的法向速度場；t為時間變量。

為克服傳統(tǒng)水平集方法的數(shù)值問題，便于與梯度優(yōu)化算法結合，本文采用緊支徑向基函數(shù)插值替代離散的水平集函數(shù)，形成參數(shù)化水平集法[16]。在參數(shù)化水平集法中引入局部水平集函數(shù)，可有效避免初始擴展系數(shù)求解困難的問題[17-18]。

(4)

式中：φ為緊支徑向基函數(shù)插值矩陣；α為擴展系數(shù)向量，其中，k=1,…,N，N為細觀結構設計域緊支徑向基插值控制點的數(shù)量。

根據(jù)式(4)，參數(shù)化之后的局部水平集函數(shù)法向速度場為

(5)

1.2 周期性多孔結構物理描述

本文采用子結構法[19]描述多孔結構物理模型，如圖2所示。將多孔結構單胞凝聚為具有多個節(jié)點的超單元。與周期性多孔結構的幾何描述定義類似，子結構法的基本思想是將計算域Ω分解為若干子區(qū)域Ωi，先求解邊界上的數(shù)值信息，然后對子區(qū)域內(nèi)部“各個擊破”。在有限元分析中采用子結構法可以實現(xiàn)多孔結構物理模型和幾何模型的匹配，縮小有限元分析的計算規(guī)模，降低計算內(nèi)存的消耗，提高周期性多孔結構特征值分析與拓撲優(yōu)化的效率。

圖2 子結構凝聚

特征值問題的有限元平衡方程為一個無阻尼自由振動系統(tǒng)，為了展示子結構法動態(tài)凝聚也適用于考慮載荷的動力學問題，在特征值問題中引入載荷向量F=0，則特征值問題平衡方程的矩陣形式為

(6)

(7)

由式(7)第二行可得主節(jié)點位移和從節(jié)點位移之間的關系

(8)

對于靜態(tài)凝聚，忽略式(8)中所有的慣性項

KsmUm+KssUs=Fs

假設Kss為正定矩陣，且結構內(nèi)部的從節(jié)點不受外載荷作用，即Fs=0

(10)

由式(10)得到變化關系

(11)

式中，Tc為靜態(tài)凝聚的變換矩陣

(12)

根據(jù)式(11)和式(12)，縮減后的平衡方程為

(13)

其中

(14)

(15)

由于式(9)忽略了全部慣性項，對于特征值問題，式(13)的縮減精度存在較大誤差，需要對此進行改進。由式(13)可得

(16)

對式(10)求二階導數(shù)

(17)

將式(16)代入式(17)

(18)

將式(16)和式(18)代入式(8)

(19)

對于無阻尼自由振動問題，主、從節(jié)點上的載荷Fs和Fm均為零，式(19)可進一步簡化為

(20)

由此得到子結構動態(tài)凝聚的變換矩陣

(21)

其中

經(jīng)過子結構動態(tài)凝聚后的無阻尼自由振動平衡方程為

(23)

其中，縮減后的質(zhì)量矩陣和剛度矩陣分別為

(24)

(25)

單一結構的凝聚可通過式(23)實現(xiàn)，周期性多孔結構則涉及多個子結構的凝聚。由于周期性排布的假設條件，含有重復結構特征的子結構只需進行一次凝聚，多個重復子結構的凝聚過程可通過對單個凝聚子結構的組裝完成。由于載荷向量一般取零，多個重復子結構組裝而成的縮減平衡方程為

(26)

(27)

(28)

為驗證子結構動態(tài)凝聚求解特征值問題的精度，與子結構靜態(tài)凝聚、全自由度有限元模型進行對比分析。如圖3所示為對比分析的模型，尺寸為1 m×1 m二維正方形板，厚度為0.1 m，左下角和右下角固定約束，離散為40×40個雙線性四邊形單元，單元尺寸為0.025 m×0.025 m。材料彈性模量為200 GPa，泊松比為0.3，質(zhì)量密度為7 800 kg/m3。

(a) 全自由度模型

表1為有限元分析的特征頻率值，與全自由度有限元分析對比可知，子結構靜態(tài)凝聚求解的特征值誤差較大，隨著階數(shù)的增大，特征頻率誤差越來越大。子結構動態(tài)凝聚求解的特征值誤差較小，且誤差不會隨著階數(shù)的增加而放大。因此，子結構動態(tài)凝聚能保證特征值求解的精度，同時能縮減結構自由度數(shù)量，提高特征值問題的求解效率。

表1 特征頻率對比

2 周期性多孔結構特征值拓撲優(yōu)化模型

多孔結構的共振很大程度取決于前幾階頻率，劇烈的共振一般發(fā)生在外界激勵頻率和某一階固有頻率接近的時候，所以在多孔結構設計時，必須對結構的前幾階固有頻率進行限制或改變。本文以前幾階加權特征值最大化為目標函數(shù)，構造如式所示的p-norm形式的函數(shù)，并以此緩解模態(tài)轉換引起的目標函數(shù)振蕩問題[20]。該目標函數(shù)可通過改變特征值權重ωj和p-norm函數(shù)的p值，靈活調(diào)整對全部或特定階次特征值的影響。

(29)

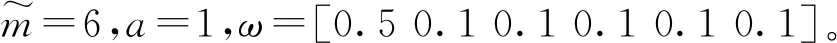
(30)

(31)

(32)

式中：ε為應變場；D為實體材料的彈性矩陣；ρ為材料質(zhì)量密度。

由于特征值λ是針對多孔結構整體的特征值，優(yōu)化模型式(30)中的目標函數(shù)并未寫成對每個多孔結構積分或累加的形式，但靈敏度表達式可寫成對子結構積分或累加的形式，其具體形式見靈敏度分析。

3 靈敏度分析與數(shù)值實施

3.1 靈敏度分析

采用形狀導數(shù)來推導目標函數(shù)和約束條件關于設計變量(擴展系數(shù))的靈敏度。根據(jù)形狀導數(shù)的定義及其引理[21]，目標函數(shù)、能量雙線性形式和載荷雙線性形式關于時間變量t的導數(shù)分別為：

(33)

(34)

(35)

將式(30)中的平衡方程兩邊對時間t求偏導得到

(36)

(37)

將式(34)、式(35)、式(37)代入式(36)可得

(38)

通過構造伴隨方程可得，該優(yōu)化問題為自伴隨問題[22]，即v=u。

(39)

根據(jù)質(zhì)量矩陣的正交歸一化條件[23]

b(u,u)=1

(40)

式(38)可進一步簡化為

(41)

式(41)仍存在邊界積分形式，引入式(42)

dΓ=δ(Φ)|?Φ|dΩ

(42)

式(41)的邊界積分轉換為體積積分

|?Φ|vndΩ

(43)

由于本文采用子結構法，式(43)可寫成對每個子結構積分的形式

(44)

γi,j(ui,λj)=εT(ui,j)Dε(ui,j)-λjρiui,jui,j

(45)

式中：下標i為子結構的編號；下標j為特征值的階次。

將式(5)中的局部水平集函數(shù)的速度場vn,i代入式(44)可得

(46)

將特征值關于時間t的導數(shù)代入式(33)可得

(47)

通過鏈式法則對目標函數(shù)J(Φ)直接求其關于時間變量t的偏導數(shù)可以得到

(48)

對比式(47)和式(48)可得目標函數(shù)關于擴展系數(shù)α的導數(shù)

φi,k(xi)dΩidΩ

(49)

同理，體積約束對擴展系數(shù)α的導數(shù)為

(50)

3.2 數(shù)值實施

結構特征值的求解是在縮減的全局有限元模型上實現(xiàn)，該過程暫不涉及子結構內(nèi)部的擴展。在求解敏度信息時，需要求解子結構內(nèi)部的特征向量。子結構內(nèi)部特征向量求解可順序求解或者CPU并行求解，CPU并行求解在子結構劃分數(shù)量較多時能節(jié)約大量時間。在求解時為避免重復計算，在子結構動態(tài)縮減時，可將式(20)中相關的數(shù)據(jù)重復使用。此外，在敏度計算時，子結構內(nèi)部特征向量的求解可重復使用子結構動態(tài)縮減中式(21)的值，這樣TIRS只需要計算一次。

為防止優(yōu)化過程中隨著結構材料的不斷刪除，出現(xiàn)無限多個特征值，需要在結構的特定位置加入所謂的非結構集中質(zhì)量。如果不加入非結構集中質(zhì)量，在結構的特定位置就不可能獲得期望的最優(yōu)拓撲結構，從而影響到整個結構頻率的最大化[24]。在周期性多孔結構設計中，單方向的周期數(shù)量可能為奇數(shù)或者偶數(shù)，非結構集中質(zhì)量的施加位置視具體情況而定，非結構集中質(zhì)量可施加在如圖4(a)所示的子結構內(nèi)部自由度上，也可施加在如圖4(b)所示的縮減結構的自由度上。加在子結構內(nèi)部時，需在子結構內(nèi)部質(zhì)量矩陣自由度所在位置的對角線上添加一個很大的數(shù)值，大小約為允許設計質(zhì)量的10%左右，非結構集中質(zhì)量會參與子結構的動態(tài)凝聚。加在縮減的結構自由度上時，需在子結構凝聚和組裝完成之后，在縮減結構的質(zhì)量矩陣自由度所在位置的對角線上添加設計質(zhì)量10%左右的數(shù)值。

(a) 子結構內(nèi)部

4 數(shù)值案例與結果分析

4.1 懸臂梁結構

如圖5所示的二維懸臂梁結構，梁結構設計域長寬比L∶H= 2 m∶1 m，厚度為0.1 m，將宏觀結構設計域劃分為20×10個子結構，子結構內(nèi)部劃分為40×40個雙線性四邊形單元，單元的尺寸為0.025 m×0.025 m，材料彈性模量E=200 GPa，泊松比v= 0.3，質(zhì)量密度7 800 kg/m3，在宏觀結構右邊界中點處施加大小為設計質(zhì)量10%的集中質(zhì)量，以多孔結構體積分數(shù)f= 0.5為約束，進行二維周期性多孔結構設計。

圖5 懸臂梁設計域

圖6所示為經(jīng)過優(yōu)化的子結構單胞、水平集函數(shù)及其組裝而成的宏觀結構，經(jīng)過162次迭代后，其最優(yōu)的目標函數(shù)值收斂到16.103，體積分數(shù)收斂到0.5，前6階頻率分別為0.398 Hz、31.621 Hz、55.398 Hz、60.04 Hz、94.633 Hz、110.121 Hz。圖7所示為前6階特征頻率對應的特征向量圖，即結構的模態(tài)振型。值得注意的是，數(shù)值算例中周期性多孔結構一階固有頻率較低，通過數(shù)值試驗分析可知，引入非結構集中質(zhì)量是導致該現(xiàn)象的主要原因。因為在整個宏觀設計域中僅定義了子結構的局部水平集函數(shù)，因此只需要對一個子結構單胞進行求解，即可得到如圖6(c)所示的20×10個周期性分布的子結構。從圖6(c)可以看出，最優(yōu)的周期性結構在集中質(zhì)量施加點處存在材料，這是由于子結構動態(tài)縮減的尺度關聯(lián)性所帶來的益處。

(a) 最優(yōu)子結構單胞

(a)

在迭代初期前6階頻率一直處于下降趨勢，這是因為初始化的結構體積分數(shù)大于指定的體積分數(shù)，迭代初期的約束條件不滿足，導致前6階頻率較大，如圖8所示。當體積分數(shù)約束得到滿足后，隨著優(yōu)化過程的進行，前6階頻率逐漸收斂。

圖8 前6階頻率迭代圖

4.2 兩端固定梁結構

為驗證本方法的高效性和特征值問題的尺度效應，考慮如圖9所示的兩端固定的二維梁結構，將本方法與沒有模型縮減的全自由度拓撲優(yōu)化[25]的計算時間進行了對比。梁結構設計域長寬比L∶H= 7 m∶1 m，厚度為0.1 m，將宏觀結構設計域分別劃分為14×2、28×4、56×8和84×12個子結構，子結構內(nèi)部劃分為40×40個雙線性四邊形單元，單元的尺寸為0.025 m×0.025 m，材料彈性模量E=200 GPa，泊松比v= 0.3，質(zhì)量密度7 800 kg/m3。在結構中心施加大小為設計質(zhì)量10%的集中質(zhì)量，以子結構體積分數(shù)f= 0.5為約束，進行二維周期性多孔結構設計。

圖9 兩端固定二維梁設計域

當宏觀結構離散為14×2、28×4、56×8和84×12個子結構時，其結構自由度數(shù)量分別約為9萬、36萬、144萬和323萬，采用子結構法分別將其縮減至約為0.57萬、2萬、7.6萬、17萬。如表2所示為對應4種子結構數(shù)量下的拓撲優(yōu)化結果。其中最優(yōu)子結構拓撲構型的特征在于上下兩端有橫向分布的主承載結構，主承載結構之間有交叉的結構。隨著子結構數(shù)量的增多，最優(yōu)子結構的拓撲構型在局部展現(xiàn)出一定的變化，其目標函數(shù)也隨之下降。圖10所示對應4種子結構數(shù)量下周期多孔結構特征頻率的變化趨勢，在固定大小的設計域內(nèi)，當離散的子結構數(shù)量越多時，優(yōu)化結果表現(xiàn)出一定的尺度效應，其最優(yōu)多孔結構的前6階特征頻率整體呈下降趨勢。因此，在實際工程應用中，可

圖10 多孔結構特征頻率變化

表2 特征值拓撲優(yōu)化結果

針對結構具體的力學性能需求來設置多孔結構周期性排布的數(shù)量，從而避開結構的激振頻率。

在拓撲優(yōu)化的計算效率方面，如圖10所示，對比本文子結構法與全自由度模型，當子結構數(shù)量為14×2時，在每一步迭代中，兩種方法在有限元分析和拓撲優(yōu)化的平均計算時間相當。當子結構數(shù)量大于14×2后，在每一步迭代中，本文方法在有限元分析和拓撲優(yōu)化方面的平均計算時間大幅下降。當子結構數(shù)量為84×12時，本文方法優(yōu)化更新的計算時間僅為全自由度模型的19.4%，有限元分析的計算時間僅為全自由模型的31.9%，平均每步的迭代時間約為全自由度模型的30.5%。其原因在于，本文采用了子結構動態(tài)凝聚縮減了自由度數(shù)量，采用了局部水平集函數(shù)描述多孔結構降低了幾何描述上的復雜度，從幾何模型和物理模型角度共同提升了周期性多孔結構特征值拓撲優(yōu)化的效率。此外，從圖11可知，有限元分析占據(jù)了拓撲優(yōu)化大部分的計算時間，研究高效的有限元分析方法將有助于提升拓撲優(yōu)化的計算效率。

圖11 計算效率對比

4.3 三維梁結構

如圖12所示的兩端固定的三維梁結構，結構設計域長寬高比例為L∶W∶H= 7 m∶1 m∶1 m，將結構設計域劃分為14×2×2個三維子結構，每個子結構離散為10×10×10個八節(jié)點六面體單元，單元的尺寸為0.1m× 0.1 m × 0.1 m，材料彈性模量E= 200 GPa，泊松比v= 0.3，質(zhì)量密度7 800 kg/m3。在結構中心施加大小為設計質(zhì)量10%的集中質(zhì)量，以多孔結構體積分數(shù)f= 0.4為約束，進行三維周期性多孔結構設計。

三維結構的有限元分析和子結構的凝聚相對于二維問題具有更大的計算量，本算例采用三維子結構法將結構自由度從18.6萬左右縮減至約4.2萬。如圖13所示為經(jīng)過優(yōu)化的三維周期性結構及其子結構單胞，從子結構單胞拓撲構型可知，組裝后的周期性多孔結構在集中質(zhì)量點處必然存在材料，這是子結構法尺度關聯(lián)所帶來的益處。從圖14可知，拓撲優(yōu)化模型經(jīng)過93次迭代后，其最優(yōu)的目標函數(shù)值收斂至36.564 7，體積分數(shù)收斂至0.4。圖15所示為前6階頻率迭代圖，分別收斂至1.558 Hz、36.049 Hz、68.633 Hz、82.604 Hz、82.814 Hz、106.298 Hz。

圖13 三維周期性多孔結構優(yōu)化結果

(a)

圖15 前6階特征頻率迭代圖

5 結 論

子結構法是高效、高精度的模型縮減方法，本文將參數(shù)化水平集方法和子結構動態(tài)凝聚相結合，研究了周期性多孔結構的特征值拓撲優(yōu)化方法。研究表明，本方法能有效實現(xiàn)尺度關聯(lián)的二維和三維周期性多孔結構的特征值拓撲優(yōu)化，且所設計的周期性多孔結構具有一定的尺度效應。