新型豎向電渦流-磁力混合阻尼裝置試驗研究

朱前坤, 馬齊飛, 張 瓊, 杜永峰

(蘭州理工大學 防震減災研究所， 蘭州 730050)

隨著城市化的邁進和建筑行業的飛速發展，出現了大量輕質、柔性結構[1]。這些結構，具有阻尼低，頻率低等特點[2]。一旦激勵荷載的頻率和結構接近，會發生共振，產生較大響應，嚴重時還會造成結構破壞，危害人身和財產安全[3]。為解決此類問題，最常用的措施是對結構進行被動控制[4]。

被動控制中以調諧質量阻尼器(tuned mass damper,TMD)減振控制備受青睞。常用的阻尼器有橡膠阻尼器[5]，液體黏滯阻尼器[6]和電渦流阻尼器[7]等。其中橡膠阻尼缺點是容易老化[8]；液體黏滯阻尼器不易養護，且會有漏油現象[9]；電渦流阻尼器因剛度和阻尼可分離而備受關注[10]。

TMD減振原理是結構受到外力作用發生振動帶動TMD運動，TMD運動過程中對結構施加一個反向的慣性力，以此控制結構的振動[11]。現在國內外學者已經對電渦流阻尼器進行了大量研究：其中Lee等[12]采用近似理論對渦流制動控制器模型進行了分析，并通過試驗得出渦流阻尼力與速度成正比的結論。汪志昊等[13]提出了一種電渦流TMD構造與磁路優化設計的方法，通過有限元仿真和試驗確定其最優間距、運動方向、相鄰永磁體磁極宜同向布置。Kwak等[14]通過在懸臂梁的末端連接一個柔性結構、兩個永磁體和固定銅板，永磁體運動改變穿過銅板的磁通量，產生電渦流。Sodano等[15]通過在導體板外側放置第二個磁性相反的磁鐵來壓縮磁場，從而提高磁通量來提高阻尼力。而實際應用中電渦流阻尼器存在漏磁現象，最優阻尼比也很難達到，有時僅用一種阻尼形式很難達到最佳控制效果。需要引入一種新的阻尼與電渦流阻尼進行混合減振。磁力在減振應用中研究頗多：Sebastian[16]提出了一種新型的旋轉對稱磁力阻尼器，并通過試驗證明這種磁阻尼器對風力渦輪機上的振動有較好的減振控制效果。Fune等[17]利用兩個磁性橡膠層制作了磁力減振器，其原理是由滑動摩擦產生的這種摩擦損失與由磁性橡膠層變形產生的內部損耗同時作用,因此減振效果非常顯著。汪志昊等[18]提出了一種基于永磁體作用力的頻率調節方法，通過調整永磁體相互作用力帶來的附加剛度調節擺式調諧質量阻尼器的頻率。李輝等[19]提出了一種磁懸浮減振器的設計方案，磁懸浮減振器的彈性介質是兩塊同極相對的高強度永久磁鐵，分析比較表明，它的綜合性能優于螺旋彈簧。Zhou等[20]用梁彈簧與由電磁體和永磁體構成的磁性彈簧并聯，進行了被動、半主動控制，結果表明該裝置控制效果顯著。上述學者所研究的并聯磁鐵將提供負剛度，且磁力減振技術大多應用于車輛減振中，在土木工程領域鮮有所聞。

本文提出了一種電渦流-磁力阻尼器(eddy current-magnetically tuned Mass damper,EMTMD)。首先介紹了EMTMD的減振原理及其對結構減振控制的運動方程。接著介紹了EMTMD的設計方法，并提出了一種磁力附加剛度和等效磁力阻尼系數的計算方法。然后對不同磁路設計的EMTMD進行試驗，測量自身的動力參數。最后用其對結構模型進行減振控制，計算出各個工況下的減振率，進而得出EMTMD不同工況對結構振動控制效果的不同影響。

1 減振原理及振動方程

1.1 EMTMD的工作原理

電渦流-磁力阻尼系統是由永磁鐵和導體板組成的電渦流阻尼系統和兩組相對磁鐵組成的磁力阻尼系統構成，如圖1所示。其耗能原理主要為渦流損耗和磁滯損耗兩種。渦流損耗是導體板在磁場中做切割磁感線運動，磁通量改變形成電渦流，發熱耗散振動的能量[21]。磁滯損耗是鐵磁體等在反復磁化過程中因磁滯現象而消耗的能量，這部分能量轉化為熱能，以此耗散振動的能量[22]，因而達到結構振動控制的目的。

圖1 EMTMD設計樣機圖

1.2 結構振動分析模型

豎向結構受到激勵時，會產生豎向振動。豎向阻尼器控制豎向振動時，可將全部質量集中成單點。磁力可增加EMTMD的附加剛度[23]。豎向EMTMD的簡化計算模型如圖2所示。

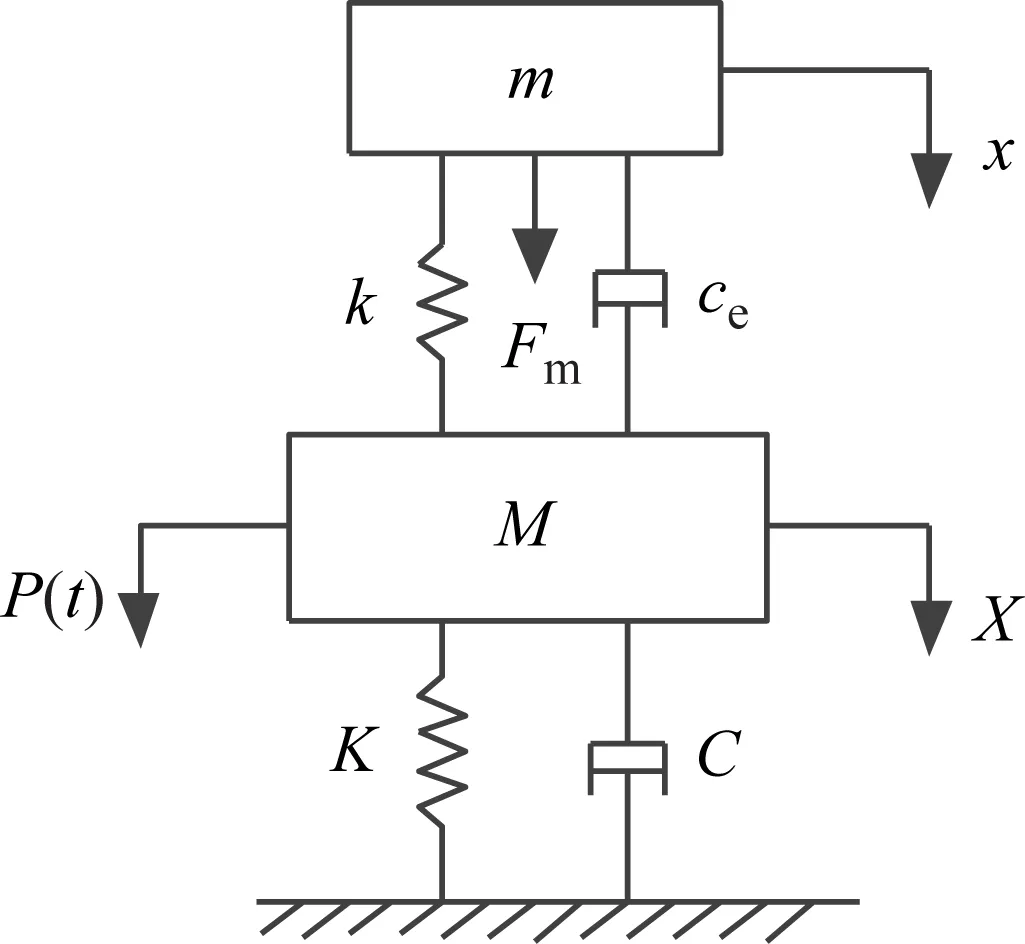
圖2 EMTMD控制結構的計算模型

圖2中：M為主結構的質量；K為主結構的剛度；C為主結構的阻尼系數；X為主結構的響應位移；m為EMTMD裝置的質量；k為EMTMD裝置的剛度；ce為EMTMD裝置的阻尼系數；x為EMTMD裝置的響應位移；Fm為磁鐵磁力;P(t)為外部激勵荷載。

特定磁路設計的磁力給EMTMD提供負剛度，其定義為在外部荷載變化量與變形變化量方向相反的情況下，剛度為負剛度[24]，對結構和EMTMD列運動平衡方程如下

(1)

式中：km為結構的附加剛度；C1為裝EMTMD裝置系統的總阻尼系數，C1=C+ce。文獻[25]也將磁鐵等效為彈簧，故本文定義km為附加剛度。故定義磁力Fmsinθ=km(x-X)，代入式(1)

(2)

其中兩磁鐵間磁力簡化公式[26]為

Fm=(Bg/4 965)2Ag

(3)

式中：Bg為磁感應強度，Gs(1 Gs=1×10-4T);Ag為磁極面積。

永磁體為長方體的一對平行吸力型永磁體間隙中點磁感應強度為[27]

(4)

式中：Br為永磁體剩磁感應強度；Lm為永磁體高度；h為一對永磁體間隙；a為磁鐵長度；b為磁鐵寬度。其中[28]

Br=μ0·Jm

(5)

式中：μ0為真空磁導率；Jm為永磁體束縛面的電流密度。

2 EMTMD的設計

2.1 結構模型的動力特性

本次選用試驗室的結構模型為試驗對象，如圖3所示。結構模型長為10 m，寬為1.6 m。由5塊2.0 m×1.6 m的雙層夾膠鋼化玻璃(厚25 mm)組成橋面，粘接在由兩根10 m的25a型工字鋼和6根1.6 m的25a型工字鋼焊接形成鋼框架主體上。鋼框架搭接在支座上，支座采用地腳螺栓錨固連接在地面。

圖3 結構模型圖

本文中只控制結構模型的豎向振動。測得該結構模型靜載下前三階的自振頻率分別為4.14 Hz，6.20 Hz和15.50 Hz，結構一階模態質量m1=795 kg。結構模型發生豎向振動時，中間位置振動最為劇烈[29]，如圖4所示，為一階振型位移峰值處。因此EMTMD需要安裝中間位置控制結構模型的豎向一階振動。

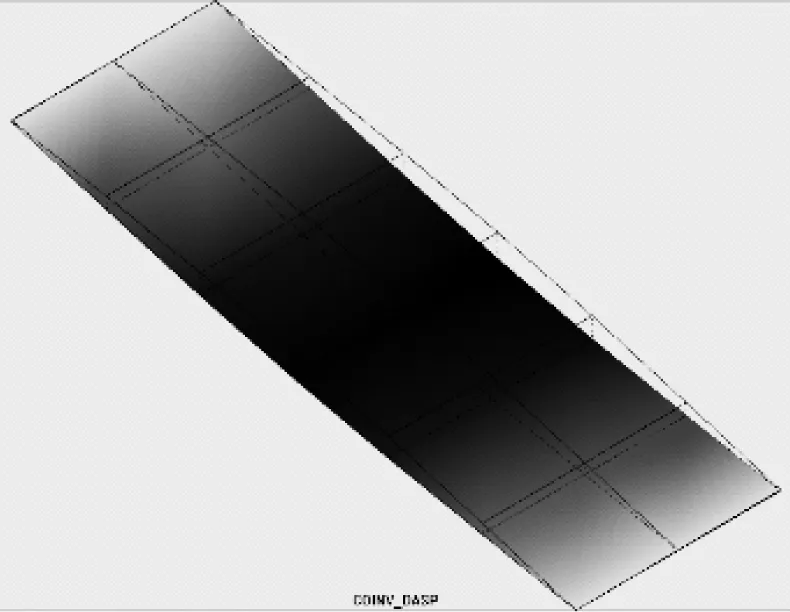
圖4 結構模型的第一階豎向振型圖

為探究EMTMD對結構模型振動控制的效果，首先必須確保激勵的一致性。本試驗選用APS400激振器，質量為75 kg，占一階模態質量的9.4%。考慮激振器的質量對結構模型一階頻率的影響，將其放入結構跨中，測得豎向一階頻率為4 Hz，激振器自質量使結構一階頻率下降0.14 Hz。然后根據結構模型的動力特性，確定EMTMD的設計參數。

2.2 EMTMD的參數設計

EMTMD的特色在于在銅板后或者底板上安裝磁鐵，該磁鐵和質量塊運動磁鐵磁心相對，相斥或相吸。增加磁鐵，會改變阻尼器的剛度和頻率。為此提出了一種假設試驗法來確定EMTMD的參數，即先根據電渦流阻尼器的要求進行參數設計，然后增加磁鐵之后通過改變質量調節頻率即可提高阻尼器的魯棒性。

設計TMD需先確定其有效質量與結構模態質量之比μ。通常μ越大，對結構振動控制效果越好。但受成本和安裝空間等因素制約，質量比一般取1%～5%[30]，本文μ取2%，則TMD運動質量為15.9 kg，振動頻率為4 Hz。由文獻[31]可知

(6)

(7)

md=μm1

(8)

式中：μ為TMD質量與結構模態質量的質量比；fopt為TMD與結構模態的最優頻率比；kopt為TMD的剛度；md為TMD的質量；copt為TMD的阻尼系數；ω1為結構的一階圓頻率；m1為結構的一階模態質量。

2.3 剛度構件

TMD應配備嚴格的導向系統，它產生的摩擦阻尼要盡量小[32]。因此本文通過無摩擦且導向性能好的4個直線套筒結構進行導向，選用4根螺旋壓簧。單根彈簧的剛度系數即為2.411 kN/m，螺旋彈簧的剛度計算式[33]

(9)

式中:G為彈簧鋼的剪切模量；D為彈簧的中徑；n為彈簧的有效圈數；d為彈簧絲的線徑。

計算得到各參數如表1所示。為了提高穩定性，選用的壓簧中徑應適當加大，故彈簧剛度會略微增加。表1對應的彈簧剛度系數為2.85 kN/m。

表1 壓簧的設計參數

2.4 電渦流-磁力阻尼構件設計

依據EMTMD的工作原理，分別設計電渦流阻尼元件和磁力阻尼元件。中指出電渦流TMD受到的電渦流阻尼力與其速度的比值即為電渦流阻尼系數。對于電渦流阻尼元件設計，電渦流阻尼系數簡化公式[34]

ce=σδSB2

(10)

式中：σ為導體板的導電系數；δ與S分別為導體板的厚度與有效表面積；B為導體板表面主磁感應強度的大小。

由式(9)可知，在同等條件下，導體板的厚度、導電系數、內外主磁感應強度的平方和電渦流阻尼的大小成正比。而磁場強度的大小又與永磁體磁性的強弱及磁路的設計密切相關。釹鐵硼(NdFeB)是目前性價比最高的磁鐵，磁性極高。試驗采用N35牌號NdFeB矩形永磁體，其主要參數有：剩磁感應強度1.2 T；最大磁能積為2.8×105Jm-3；矯頑力與內稟矯頑力分別為8.7×105A/m、9.6×105A/m；長(a)×寬(b)×高(h)分別為50 mm×30 mm×10 mm。導體板選用導電系數較高的紫銅，電導率為σ=5.8×107S/m。銅板尺寸為100 mm×100 mm×6 mm,距離磁鐵9 mm處用高斯計測量得到磁通量為0.162 T，由此計算出單塊永磁體阻尼系數為13.64 N·S/m。由于磁力也將提供阻尼，對其研究較少，阻尼系數尚沒有完善的理論公式用于計算。為避免過阻尼對試驗結果造成的影響，保守計算，僅選取兩塊永磁體，其對應電渦流阻尼系數為27.28N·S/m。然后安裝磁力阻尼元件。根據磁鐵的安裝位置，設計了3種電渦流-磁力阻尼器如表2所示。選取第3種磁路設計如圖1所示。

表2 EMTMD磁路設計

假設安裝磁力阻尼元件后，質量塊和彈簧剛度不變，振動頻率以結構的一階頻率f1計算。先測量EMTMD的自由衰減曲線，經過傅里葉變換得到自振頻率f，則EMTMD的剛度公式為

k=(2πf)2md

(11)

式中，k為EMTMD的總剛度。由于彈簧和等效磁力彈簧是并聯，故磁力提供的附加剛度為

km=k-ks

(12)

EMTMD的質量計算公式

(13)

然后測量得到無阻尼系統時TMD的固有阻尼比，阻尼系數計算公式[35]

c0=2mmω0ζ0

(14)

式中：ω0為TMD固有圓頻率；ζ0為TMD未安裝阻尼原件的固有阻尼比。

EMTMD運動過程中，磁滯損耗耗能，磁力也會提高EMTMD自身阻尼比。由磁鐵產生的阻尼系數稱為等效磁力阻尼系數。因此EMTMD運動過程中受到的阻尼分別來自電渦流阻尼、磁力阻尼、TMD無任何耗能原件時的固有阻尼。因此EMTMD總的阻尼系數即為三者之和。故c0+cm+ce=2mmωmζ，所以EMTMD的磁力阻尼系數試驗值為

cm=2mωmζ-c0-ce

(15)

式中：ωm為EMTMD固有圓頻率；ζ為安裝電渦流-磁力阻尼系統TMD的阻尼比。

2.5 豎向EMTMD的制作

根據EMTMD的參數設計，制作了可調質量的豎向EMTMD樣機。質量塊由6塊鋼板焊接形成的長方體空腔和填充的沙子組成，鋼板質量為11 kg，可調節質量為7 kg，如圖5所示。質量塊與底板通過套筒連接。質量塊和底板通過4對內徑不同的鋼管形成套筒，安裝在4個彈簧上，彈簧承受質量塊的全部質量。磁鐵安裝在鋼板上用卡夾夾在質量塊底部，隨質量塊一起運動。底板上安裝U型卡夾固定導體板。

圖5 EMTMD樣機

3 EMTMD性能測試與分析

將制作的EMTMD樣機進行試驗，首先進行其自身阻尼比的測量。測量阻尼比常用方法有[36]：半功率點法；自由衰減法；共振頻率法；放大系數法。本文選用自由衰減法測量EMTMD的阻尼比。

3.1 EMTMD阻尼比測定

EMTMD的頻率和結構自振頻率相近時，對結構能起到較好的控制效果[37]。因此首先通過試驗來調節TMD的頻率。將阻尼器質量塊按壓到可運動的最大位移處，釋放使其自由衰減。測得的加速度時程衰減曲線經過傅里葉變換得到自振頻率。通過改變質量直至頻率調節為4 Hz，然后計算阻尼比。通過多次試驗，最終調節質量塊質量為17.38 kg，此時固有頻率為4.069 Hz。

電渦流TMD計算阻尼系數時需要測量磁鐵到導體板的磁通量。考慮到可能會有漏磁現象發生，因此保守測量，即分別用高斯計測量磁鐵上3個點(a/2，b/2)(a/2，0)(0，b/2)到導體板的平均磁通量B值來計算，如見表2。電渦流TMD的理論預測阻尼比計算公式為[38]

(16)

式中：md為TMD的運動質量；ω0為TMD的圓頻率。通過式(16)計算電渦流阻尼器阻尼比為3.06%，由于實物存在漏磁的現象，試驗值將小于計算值。因此在EMTMD阻尼系數計算過程中，為避免電渦流阻尼系數計算值過于偏大，計算值應乘以縮小系數。定義縮小系數=電渦流阻尼器測量阻尼比/電渦流阻尼器理論預測阻尼比。

由于磁力TMD的相關研究較少，因此EMTMD-2、MTMD-3僅測量距上下磁鐵表面1 mm處和中間位置的磁通量作為參考。為避免質量比不同，本文質量取統一，然后測試磁鐵對EMTMD自身的影響。根據磁鐵的尺寸對其進行編號為10 mm×10 mm×5 mm(1)、20 mm×10 mm×5 mm(2)、30 mm×10 mm×5 mm(3)、20 mm×20 mm×5 mm(4)、40 mm×20 mm×5 mm(5)、20 mm×10 mm×10 mm(6)、20 mm×20 mm×10 mm(7)、30 mm×10 mm×10 mm(8)、30 mm×20 mm×10 mm(9)、40 mm×20 mm×10 mm(10)10組。現有研究中并聯磁鐵提供負剛度會有很好的減振效果，故本研究提供正剛度的僅選取一組作為對照。試驗測得磁鐵吸力對EMTMD-1提供正剛度，斥力對EMTMD-2提供正剛度。故EMTMD-1磁鐵選用編號為2，吸力僅一組。而磁鐵斥力的磁路設計提供負剛度，分別選用編號：1、2、3、4、5、6、8、9、10。EMTMD-2磁鐵選用編號為10，斥力僅一組。磁鐵斥力的磁路設計分別選用編號： 3、6、7、8、9、10。對于EMTMD-3為方便尋找最優磁路設計，先確定EMTMD-2對電渦流影響較小，且減振性能提升最高的底板磁鐵，然后控制銅板后磁鐵的尺寸為變量來對比每種組合的減振率。在此底板吸力磁鐵暫定為編號9，銅板后斥力磁鐵編號為1、2、4、7、8。后續將根據EMTMD-1和EMTMD-2對結構的振動控制效果做出適當調整。

經過試驗測得安裝不同磁鐵的3種EMTMD的頻率和阻尼比。試驗結果如表3所示(表3中數據均已減去TMD自身阻尼比0.8%)。

表3 不同磁鐵下EMTMD參數測量及計算

通過表3數據分別用式(16)、式(10)、式(15)算出結構阻尼系數、電渦流阻尼系數、等效磁力阻尼系數。具體如圖6所示。

由表3和圖6可知：EMTMD-1是吸力、EMTMD-2是斥力的磁路設計，能增加自身的正剛度，從而增加頻率；EMTMD-1是斥力、 EMTMD-2是吸力的磁路設計，會增加自身的負剛度，從而減少頻率。EMTMD-1的電渦流阻尼系數和磁力阻尼系數由編號1的17.14N·S/m和4.59 N·S/m，到編號10的2.58 N·S/m和26.49 N·S/m，說明斥力能減少電渦流阻尼系數，增大等效磁力阻尼系數；EMTMD-2的電渦流阻尼系數和磁力阻尼系數由編號3的16.72 N·S/m和5.98N·S/m，到編號10的16.96 N·S/m和4.84 N·S/m，說明電渦流阻尼系數和等效磁力阻尼系數比較穩定；EMTMD-3的電渦流阻尼系數和磁力阻尼系數由編號1的10.05 N·S/m和12.37 N·S/m，到編號9的1.78 N·S/m和32.89 N·S/m，說明底板磁鐵一定，增加銅板后磁鐵的表面積或厚度，都會降低頻率，降低電渦流阻尼系數，提高等效磁力阻尼系數。

為了更直觀的表現頻率和負剛度的關系，由式(11)計算出磁力附加剛度，并將數據繪如圖7所示。

圖7 EMTMD的頻率和負剛度變化曲線

由圖7可知，EMTMD-1、EMTMD-2、EMTMD-3的頻率變化分別由4.045 Hz到3.096 Hz；4.056 Hz到3.945 Hz；3.954 Hz到3.896 Hz。對應的附加剛度變化分別為-83 kN/m到-840 kN/m；-21 kN/m到-631 kN/m；-581 kN/m到-894 kN/m。頻率和剛度幾乎為線性關系。由此表明，增加磁鐵使EMTMD頻率降低，而EMTMD的負剛度隨著頻率的降低呈線性增長。為研究電渦流-磁力阻尼器增加負剛度對結構振動控制效果的影響，需將其放在結構上進行試驗。

4 EMTMD對結構模型的振動控制

為研究EMTMD對結構的減振控制效果，將其應用于結構模型上進行振動控制。試驗裝置如圖8所示。選用APS400激振器進行激勵，結構的位移用Banner-250U激光位移計測量，結構模型的加速度用941B拾振器測量。用DG1022U信號發生器輸入激勵頻率和激勵幅值，經過AP145放大器傳輸到APS400激振器進行激勵。采集系統選用DH-5921應變采集儀和INV3060 V采集儀分別采集位移信號和加速度信號。

(a) 測量儀器位置圖

將激振器放置結構跨中，首先以4 Hz正弦激勵對結構模型進行激勵。測量得到加速度時程，通過快速傅里葉變換得到結構模型的振動頻率如圖9所示。

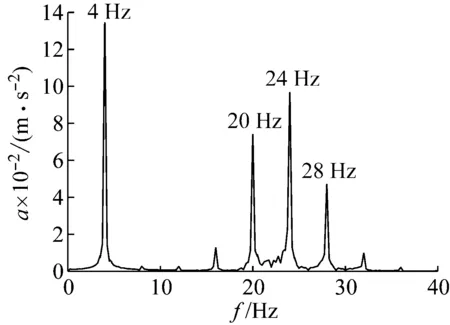
圖9 激振器4 Hz激勵下結構的加速度傅里葉變換圖

由圖9可知，結構模型的豎向振動頻率主要以4 Hz、20 Hz、24 Hz、28 Hz為主。值得指出的是，并不是當TMD頻率比嚴格等于1時，TMD的控制效果最佳，當TMD頻率比近似為1時，控制效果已可滿足工程需要[39]。本文設計的TMD僅對結構豎向一階頻率進行減振控制，磁力對頻率影響較小，且阻尼器頻率都在4 Hz左右，故為避免質量比不同帶來的影響，質量將不再改變。

4.1 安裝磁鐵為吸力或斥力的EMTMD對結構模型振動控制的影響

為探究安裝磁鐵為吸力或斥力的EMTMD對結構模型振動控制的影響，將EMTMD安裝在結構的中間位置進行振動控制。首先測量未安裝EMTMD結構模型的位移和加速度，即讓信號發生器輸出激勵頻率4 Hz，激勵幅值10 VPP使激振器激勵結構模型，發生共振，且每次輸入激勵保持一致。用拾振器測量結構中間位置的加速度；用激光位移計測量結構模型的位移，如圖10所示。然后安裝電渦流TMD，安裝磁鐵為吸力或斥力的EMTMD對結構模型進行減振控制。測量的加速度和位移時程曲線圖如11所示(僅選取EMTMD-1其中一組)。

圖10 結構模型振動控制試驗現場照片

(a) 位移時程曲線

試驗測得結構模型未安裝阻尼器時在該激勵荷載作用下位移和加速度峰值分別為8.11 mm和0.236 81 m/s2。由圖10可知，結構模型安裝電渦流阻尼器，EMTMD-1為斥力或吸力后的位移和加速度峰值分別為0.869 mm和0.023 94 m/s2，0.718 mm和0.018 865 m/s2、1.0 mm和0.027 535 m/s2。

測得EMTMD-2為斥力或吸力的磁路設計，位移和加速度峰值分別為0.8 mm和0.022 15 m/s2、0.513 mm和0.013 75 m/s2。計算得到加速度和位移減振率如圖12所示。

由圖12可知，結構模型安裝電渦流阻尼器，EMTMD-1為斥力或吸力，EMTMD-2為斥力或吸力后的位移和加速度的減振率分別為89.20%和89.80%，91.14%和92.00%、87.60%和88.30%，89.40%和90.60%、93.60%和94.10%。結構模型安裝EMTMD-1為斥力，EMTMD-2為吸力或斥力的減振率分別高于電渦流TMD的1.94%和2.20%，4.40%和4.30%、0.20%和0.80% ，而安裝EMTMD-1為吸力的減振率低于電渦流TMD的1.60%和1.00%。

(a)

盡管安裝磁力阻尼系統，EMTMD阻尼比變化微弱，但是合適的磁路設計可提高減振率，從而說明電渦流-磁力混合阻尼減振效果優于電渦流阻尼。因此磁鐵最佳磁路設計EMTMD-1應為斥力，EMTMD-2應為吸力。對于EMTMD-3的磁路設計需要結合EMTMD-1和EMTMD-2減振效果顯著的方案來設計，即銅板后磁鐵和相對的運動磁鐵表面磁性相同，底板上磁鐵和同一側的運動磁鐵表面磁性相反。確定EMTMD磁鐵的最佳磁路設計后，需進一步確定磁鐵尺寸。

4.2 磁鐵尺寸對EMTMD減振控制的影響

為探究磁鐵尺寸對EMTMD減振控制的影響，將分別在EMTMD上安裝不同磁鐵對結構模型進行減振控制。每種工況都以相同輸入進行激勵：即在信號發生器輸出激勵頻率4 Hz，激勵幅值10 VPP使激振器激勵結構模型發生共振。將上述設計的不同工況下EMTMD-1、EMTMD-2、EMTMD-3分別對結構進行減振控制。每次測量得到阻尼器穩定工作后的位移和加速度峰值如圖13所示。

由圖13可知， EMTMD-1、EMTMD-2、EMTMD-3安裝磁鐵尺寸分別為20 mm×20 mm×5 mm、30 mm×20 mm×10 mm，20 mm×10 mm×5 mm、30 mm×20 mm×10 mm減振效果最好，由式(3)和式(4)以及表3數據計算出3種工況最大磁力分別為46.69 N，81.8 N，123.22 N。此時結構模型位移和加速度峰值分別為0.611 mm和0.015 3 m/s2，0.421 mm和0.012 315m/s2，0.331 mm和0.011 15 m/s2。據此計算得到不同磁鐵尺寸下EMTMD的位移和加速度減振率分別如圖14所示。

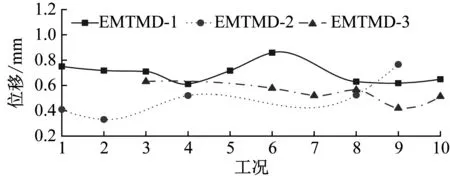
(a) 位移曲線

由圖14可知，EMTMD-1、EMTMD-2、EMTMD-3控制效果最佳的工況對應的位移和加速度減振率分別為92.49%和93.56%，94.80%和94.80%，95.90%和95.30%，對應的電渦流阻尼系數和磁力阻尼系數之比分別為0.37、3.00、0.75。在銅板后安裝磁鐵和底板上安裝磁鐵制作的EMTMD，均能在電渦流TMD減振控制的基礎上提高減振性能，但是在銅板后安裝磁鐵的磁路設計的EMTMD減振率小于底板上安裝磁鐵。其原因為銅板后安裝磁鐵會降低電渦流阻尼力，而底板上安裝磁鐵對電渦流阻尼力影響較小。

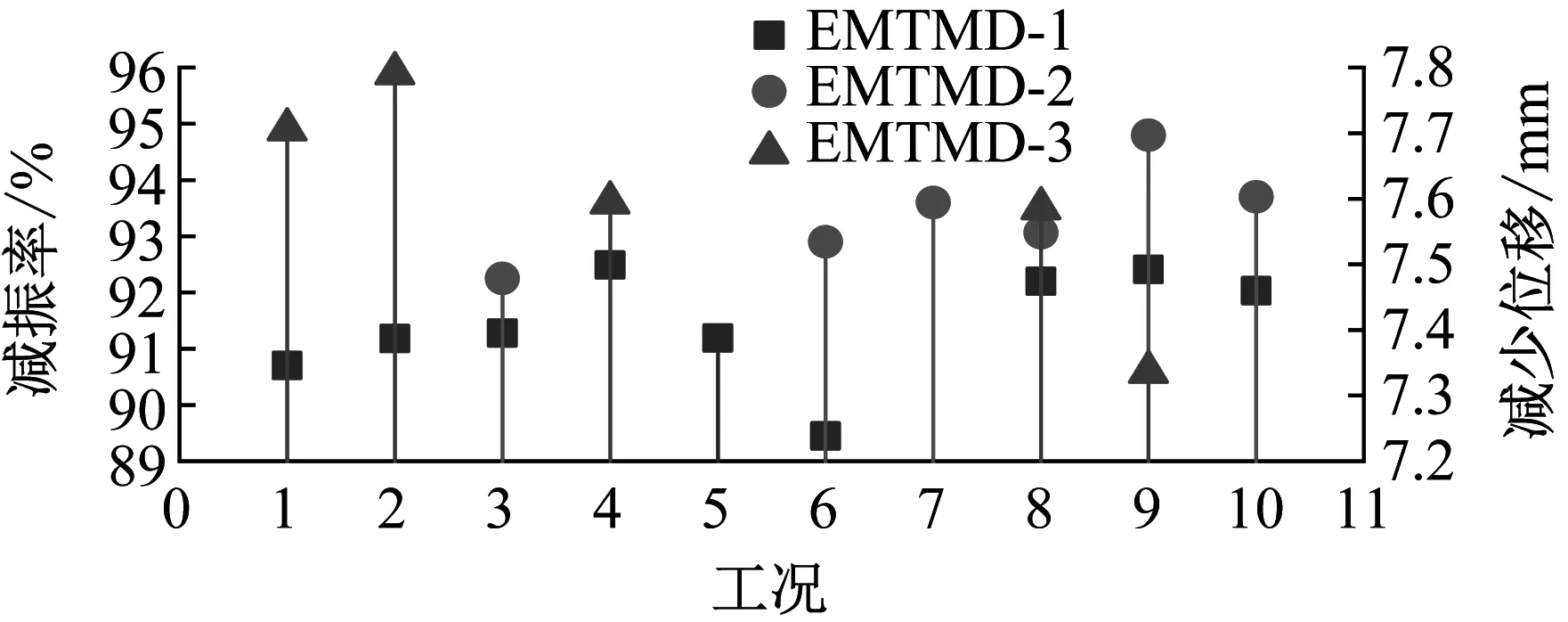
(a) 減振率-減少位移曲線

4.3 不同激勵頻率下EMTMD對結構模型的減振控制影響

為探究EMTMD對結構模型的減振控制效果受激勵頻率的影響，特將EMTMD放在結構的中間位置進行試驗。本文分別選取2 Hz、3 Hz、4 Hz、5 Hz進行激勵。當激振器激勵致使結構模型發生振動，選取TMD穩定工作以后的加速度和位移峰值作圖，如圖15所示。

(a) 頻域-位移曲線

由圖15可知，結構模型安裝電渦流阻尼器EMTMD-1、EMTMD-2、EMTMD-3后當激勵頻率為4 Hz時的位移和加速度最小，其數值分別為0.884 mm和0.023 94 m/s2，0.611 mm和0.017 6 m/s2，0.421 mm和0.017 6 m/s2，0.331 mm和0.017 6 m/s2。由此計算各個工況減振率如圖16所示。

由圖16可知，當激勵頻率為f/2、f時，結構會產生較大響應，減振率較大。當結構模型發生共振時，電渦流TMD，EMTMD-1、EMTMD-2、EMTMD-3的位移和加速度減振率分別可達89.6%和89.9%，92.5%和93.5%，94.8%和94.8%，95.9%和95.2%。同一激勵頻率，減振率EMTMD-3>EMTMD-2>EMTMD-1>電渦流TMD。說明EMTMD具有很好的減振耗能作用。從2 Hz到4 Hz，電渦流阻尼器位移的減振率變化9.1%，EMTMD-3位移的減振率變化6.2%。說明EMTMD-3對結構的控制效果比電渦流阻尼器的更加穩定。

4.4 不同激勵幅值下EMTMD對結構模型的減振控制影響

為探究EMTMD在不同激勵幅值下對結構模型的減振控制問題，特將EMTMD-3放在結構的中間位置進行試驗。輸入簡諧荷載頻率為結構自振頻率1倍能更好的保證TMD的魯棒性。為此讓激振器激勵頻率為4 Hz，激勵幅值分別為5 VPP、10 VPP、15 VPP，對結構模型進行激勵。為了進行有效對比，首先將激振器擺放在結構模型跨中，對未安裝減振裝置、安裝電渦流TMD、 EMTMD-3后的結構模型進行激勵。每次選取TMD穩定工作以后的位移和加速度峰值如表4所示。

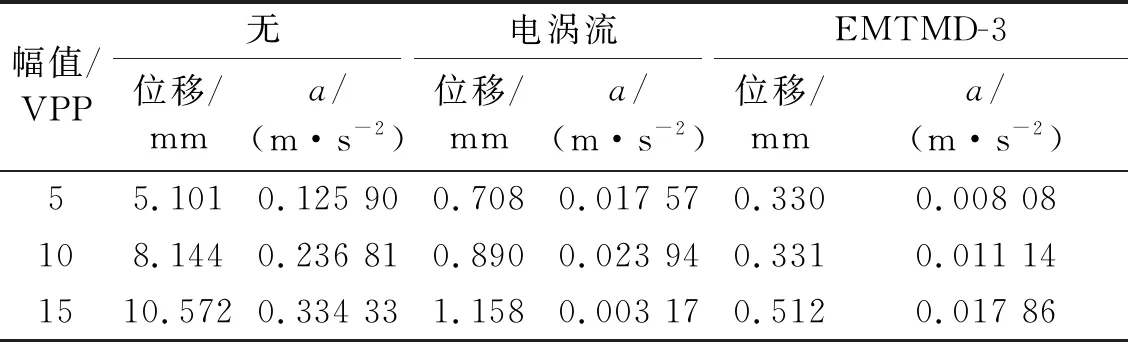
表4 不同激勵頻率下結構振動響應

由表4可知，同一激勵幅值，EMTMD-3的位移和加速度最小。結構模型安裝EMTMD-3后的位移和加速度是同工況下安裝電渦流阻尼器的1/2。同時根據表4數據計算得到加速度和位移減振率，如圖17所示。

由圖17可知，隨著激勵幅值由5 VPP變化到15 VPP，電渦流阻尼器減振率變化4.4%，EMTMD-3減振率變化2.4%。由此可見激勵越大EMTMD-3越穩定，當面對較大激勵EMTMD-3有良好穩定的減振作用。并且每種工況下，EMTMD-3減振率均高于電渦流TMD，最高可達95.9%，比同工況下電渦流TMD減振率高6.8%。電渦流TMD控制效果能夠達到EMTMD-3的92.9%，由此可知EMTMD比傳統的電渦流TMD有更好的減振控制作用。

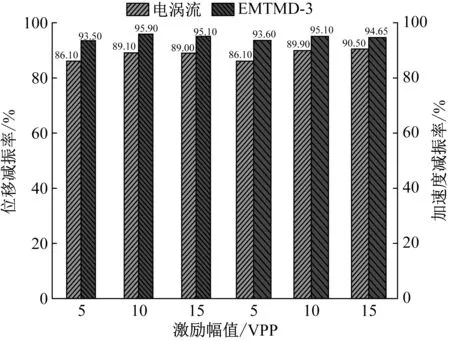
圖17 不同激振幅值下安裝電渦流和EMTMD-3的結構減振率圖

5 結 論

本文通過對EMTMD進行研究，可以得到以下結論：

(1) 研制的EMTMD裝置，由電渦流阻尼系統和磁力阻尼系統組成，利用渦流損耗和磁滯損耗一起消耗振動能量，故有很好的減振作用。

(2) 磁鐵的磁性和尺寸對電渦流-磁力阻尼器自身參數有影響。特定磁路設計可增加結構的負剛度——銅板后磁路設計應為斥力；底板上磁路設計應為吸力。一定范圍內增加磁鐵的表面積或厚度，會提高等效磁力阻尼系數，提高附加剛度。

(3) 電渦流-磁力阻尼器對結構的減振性能優于電渦流阻尼器。EMTMD-1、EMTMD-2、EMTMD-3在同等激勵條件下，減振率均高于電渦流TMD。EMTMD-3的減振率最高可達95.9%，比電渦流TMD減振率高6.8%。