聲表面波在空心圓柱體中的傳播特性分析

吳榮興, 邱森, 張青艷, 鄭東

（寧波職業技術學院應用力學研究所，浙江寧波，315800）

0 引言

聲表面波因其具有激發和接收簡單、傳播能量衰減較小、檢測領域廣泛等優點，在板型和圓柱類結構中獲得了廣泛的應用[1]。高祥熙等利用超聲表面波對飛機液壓導管的裂紋進行了檢測[2]。徐志祥等采用有限元仿真分析表面波在涂層平板表面的傳播規律，利用Morse小波分解多頻表面波信號，提取最大幅值單一頻率的缺陷時域信號從而確定表面缺陷位置[3]。宋大成等研究了聲表面波與一定深度范圍內的V型裂紋的作用過程，采用有限元方法模擬了熱彈機制下，線性脈沖激光源激發的聲表面波信號在金屬材料中的傳輸過程，以及聲表面波與V型裂紋的相互作用[4]。吳榮興等分析了聲表面波在混凝土材料特性檢測和飛機結冰厚度檢測等應用[5-7]。

金屬圓柱作為常見的結構類型，其表面缺陷檢測和管道類傳感檢測一直是檢測領域重要的方向。聲表面波在圓柱表面傳播會產生色散和相移現象，這與聲表面波在平板上的傳播規律不同，一定程度影響了檢測表面缺陷的位置精度[8]。徐志祥等提出通過掃描檢測點的方法確定缺陷的位置，給出了表面波在表面缺陷附近的傳播路徑和缺陷深度計算公式[9]。在這些分析過程中，除了極少數情況下，一般無法獲得其精確解析解，主要原因是聲表面波在空心圓柱體傳播時其邊界條件和求解過程將更加復雜。本文分析了聲表面波在空心圓柱體內傳播的特性，為聲表面波在空心圓柱體的檢測奠定了理論基礎和方法。

1 基本方程

聲表面波在如圖1所示的空心圓柱體內沿著圓周方向傳播，其內徑、外徑和圓周轉角分別為r1、r2和θ，z軸垂直于的圓柱體橫截面，文中不考慮聲表面波沿著z軸方向傳播。當聲表表面波沿著平板傳播時候，我們主要考慮二維截面，沿著x1方向傳播，但是在x2方向發生衰減。這里沿著圓周方向傳播，沿著半徑方向發生衰減。

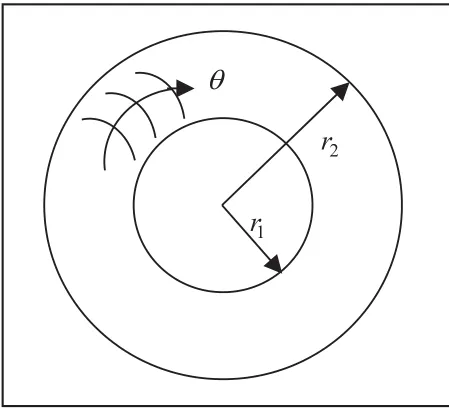
圖1 空心圓柱體截面圖

各個方向的位移可以寫為

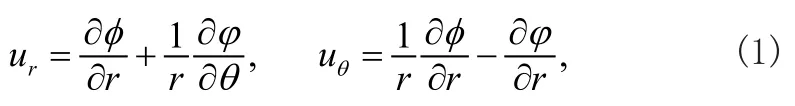
式中ur和uθ分別是半徑r和轉角θ的函數，而勢函數φ和?必須滿足圓柱坐標下的波動方程為

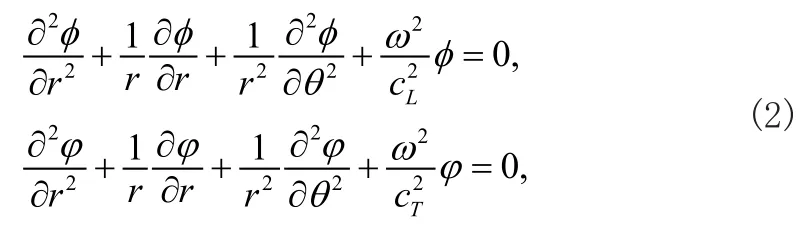
式中

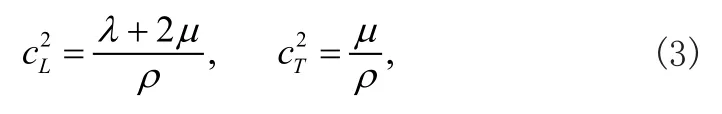
分別定義為彈性介質的縱波和橫波波速，其中,λμ和ρ分別為彈性固體的拉梅常數和密度。根據彈性材料的本構關系，應力可以表示為

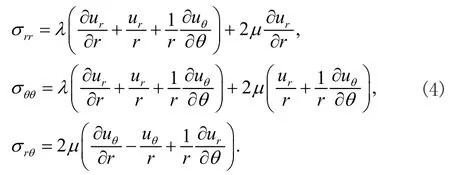
對于如圖1所示圓柱體的內外表面，其邊界條件為

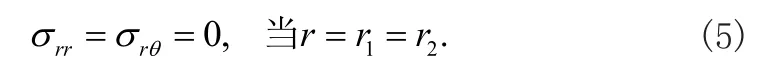
可以進一步假設勢函數為

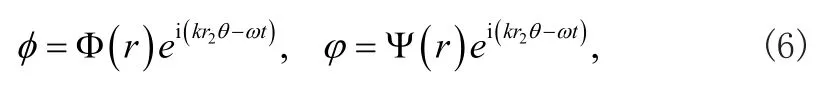
式中k和t分別式角波數和時間變量。將式(6)代入式(2)，省略掉e?iω t可以得到

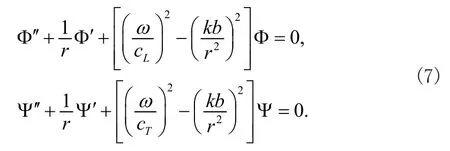
式中的通解為

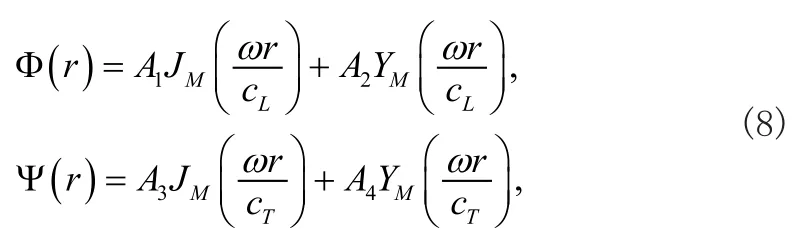
式中JM和YM分別是第一類和第二類貝塞爾函數，A1(A2,A3,A4)為振幅表示式，其他參數定義如下

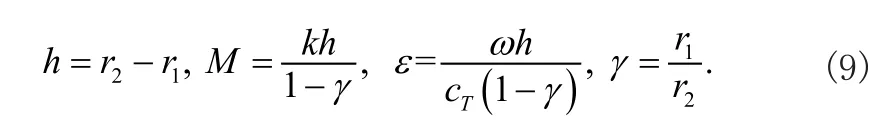
將式(8)代入應力表達式(4)，可以得到

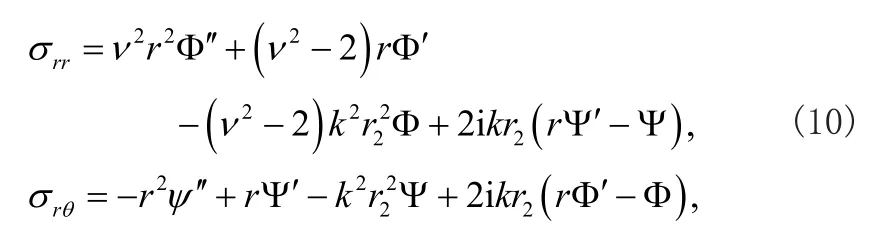
可以將應力表達式(10)代入邊界條件式(5)，可以得到振幅A1(A2,A3,A4)的線性齊次方程組。若這些振幅存在非零解，那么必須要求系數行列式的值必須為零，這樣就得了聲表面波在圓柱表面傳播的頻散方程如下

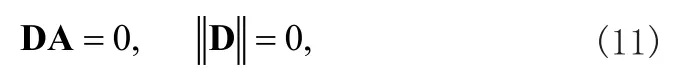
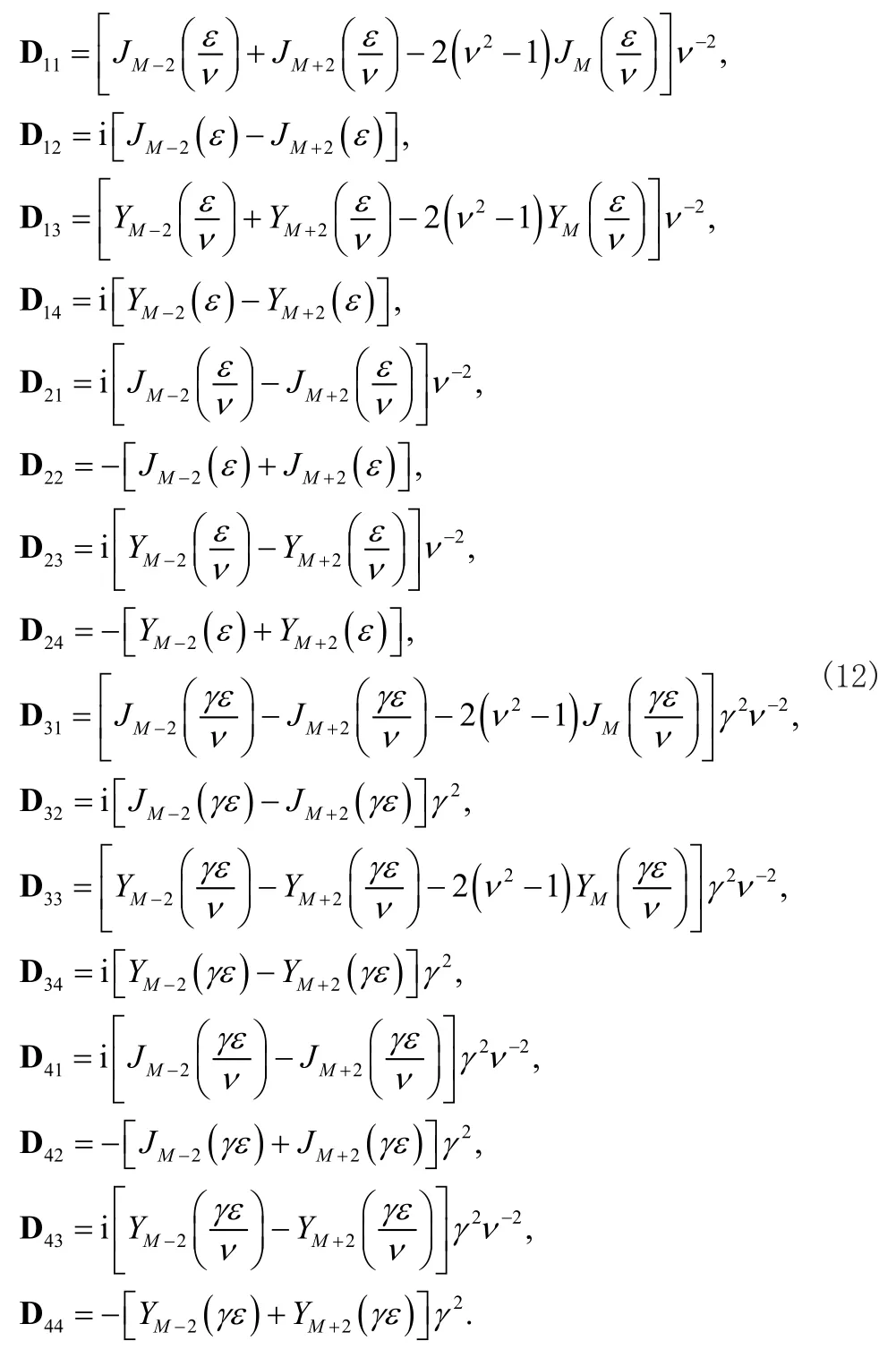
這樣就完整建立了聲表面波在空心圓柱體傳播的頻散方程。為了進一步分析其振動特性，根據式(11)的計算結果，我們可以得到多個聲表面波的解，根據線性疊加原理，可以重寫位移為

式中

通過位移表達式可以確定聲表面波的振動模態形式，主要為對稱振動和反對稱振動模態。這里的位移表達式和平板的位移表達式存在著明顯不同，平板的位移表達式是不考慮曲率的影響，因此引用的勢函數也是不同的，其表達式為

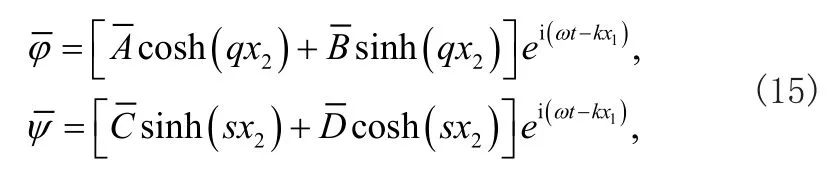
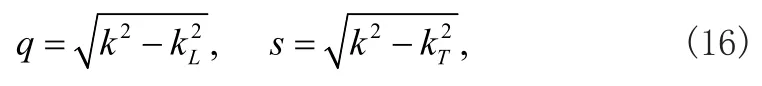
式中kL和kT分別為單層板中縱波和橫波的波數

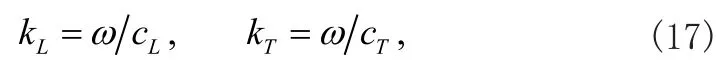
式中cL和cT分別為單層板的縱波和橫波波速，如式(3)所示。通過式(15)-(18)和前面的推導表達式比較可以明顯看出位移表達的不同，同時由于曲率的存在，聲表面波的頻率和位移都將發生改變，而這些改變對于聲表面波的檢測來說非常重要。

2 計算結果

可以對式(11)進行求解，這里設定的材料參數為空心圓柱鋁管，相關參數定義如下

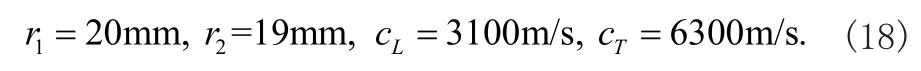
可以進一步定義周向導波的相速度為[10]

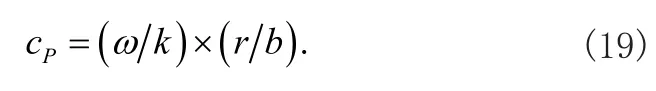
這樣繪制了不同內徑空心鋁圓柱體的聲表面波的頻散關系如圖2-3所示。

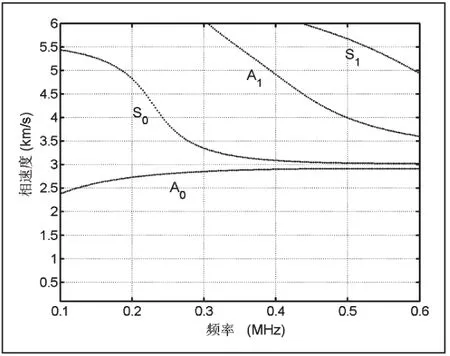
圖2 空心鋁圓柱的聲表面波頻散關系(r2=19mm)

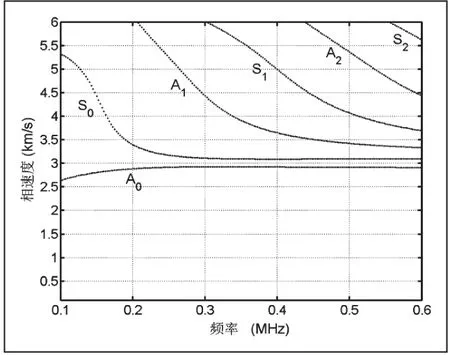
圖3 空心鋁圓柱的聲表面波頻散關系(r2=18.5mm)

從圖2-4中可以觀察到隨著頻率的增加，空心鋁圓柱中的聲表面波將會出現一系列對稱和反對稱模態，這為空心圓柱體的各類檢測提供了多模態選擇[10]。先前的研究表明低階的振動模態通常被用來作為檢測的工作模態，例如零階對稱和反對稱模態，主要原因是低階模態比較容易激發和接收信號，高階模態激發和接收需要更加精確[7]。同樣發現隨著空心鋁圓柱體壁厚的不斷增加，在同一頻率尺度內各種振動模態將出現更多，這和平面板的結果不一致[11-12]。但是與平板中傳播的聲表面波一樣，隨著頻率的不斷增加，空心鋁圓柱體內的聲表面波的各模態的波速都將趨于瑞利波波速[13]。

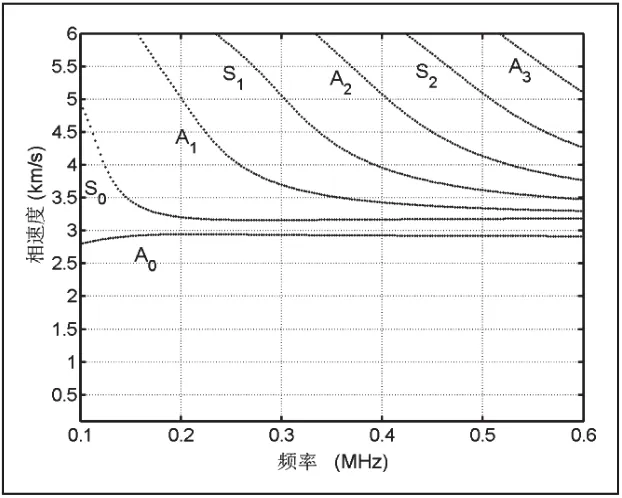
圖4 空心鋁圓柱的聲表面波頻散關系(r2=18mm)

同樣根據式（13），我們可以繪制出聲表面波在圓柱體傳播的位移圖如圖5-圖8所示。

這里需要注意的是圖5-8的縱坐標是各階模態的歸一化位移，因為在計算過程中是利用振幅比來求解聲表面波的位移，因此就不存在單位。從圖5-8可以發現，圓柱體內的聲表面波的位移仍然呈現對稱和反對稱模態[14]。但是由于存在一定的曲率，對稱和反對稱模態略顯變異，通過繪制不同曲率的位移圖表明曲率對于位移的影響較為明顯。這樣在實際工程檢測中，必須注意模態的選擇，過去的研究表明高階模態由于信號發射和接受比較困難，通常選擇低頻模態。現在的研究表明相比于平板，圓柱空心體的聲表面波的低階模態受曲率影響較為明顯，實際檢測時候必須考慮這些影響。

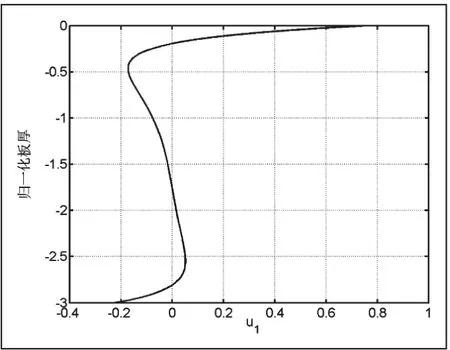
圖5 空心鋁圓柱中u1 的位移(r2=18mm)

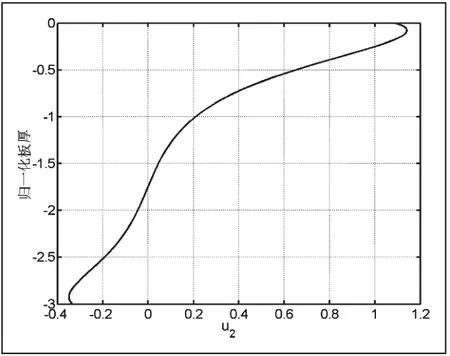
圖6 空心鋁圓柱中u2 的位移(r2=18mm)

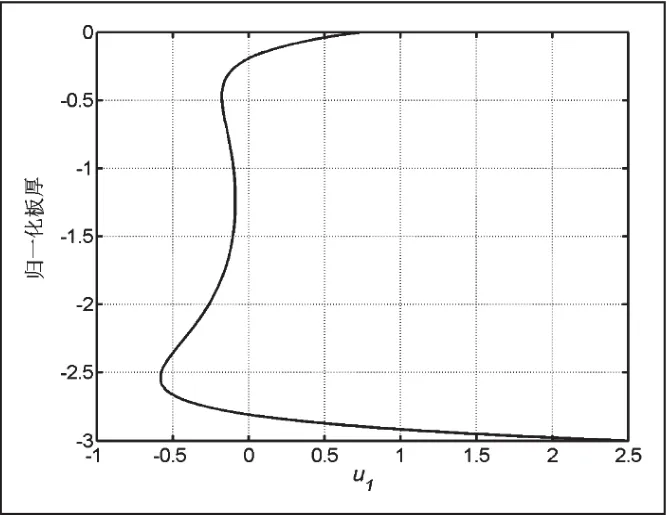
圖7 空心鋁圓柱中u1 的位移(r2=18mm)

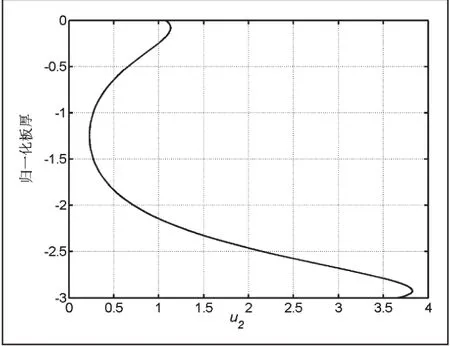
圖8 空心鋁圓柱中u2 的位移(r2=18mm)

3 結論

分析了聲表面波在空心鋁圓柱體內的傳播特性，建立了聲表面波的頻散方程。通過數值求解繪制了不同壁厚的空心鋁圓柱體的聲表面波頻散關系。計算結果表明聲表面波在空心圓柱體沿著圓周方向傳播時將會出現多個對稱和反對稱模態，同時隨著頻率的增加，各種模態的相速度都將趨于瑞利波的波速。這里建立的模型和計算結果為實際的聲表面波圓柱體檢測奠定了基礎。