受電弓氣動特性隨列車時速及工作高度變化規律的數值分析

王東屏,趙亞軍,孫成龍,黃思俊

(1.大連交通大學 機械工程學院,遼寧 大連 116028;2.北京中車賽德鐵道電氣科技有限公司,北京 100176)①

改革開放以來，我國高速鐵路的技術有了迅猛的發展，逐漸形成了高速車輛及重要零部件的自主研發與規模制造的規范體系[1].列車頂部安裝的受電弓是高速列車安全運行并取得電力的關鍵設備.隨著列車運行速度越來越快，對鐵路電氣化的要求也越來越高[2].受電弓系統作為高速列車的關鍵技術之一面臨巨大的挑戰，受電弓系統與周圍空氣的作用變得十分劇烈.例如當列車速度達到250～300 km/h時，空氣對受電弓產生的阻力約占總阻力的70%～80%[3]，而且當速度越大時，產生的阻力越大，對受電弓的影響就越大.

目前，國內許多學者對高速列車受電弓氣動特性的分析研究已取得諸多成果.林澤峰[4]等人對列車運行速度300 km/h時受電弓所處的有限個結構位移狀態下各部件的氣動力進行數值模擬,探討了受電弓氣動抬升力的傳遞系數與其工作高度的關系.張業[5]等人基于CFD軟件，采用SIMPLE算法分析了不同速度下的受電弓空氣動力特性.郭迪龍[6]等人對橫風作用下受電弓的抬升力進行仿真計算，探討了受電弓主要部件的優化方案.臧首華[7]數值模擬了高速受電弓在18種工況下的外流場，并分析了各工況下受電弓的空氣動力學特性，總結了氣動阻力、升力和側向力值在不同車速和風速下的變化規律.張雪[8]對受電弓不同速度的抬升力進行仿真計算，總結了升弓高度1 600 mm時受電弓氣動抬升力隨速度變化的規律.雖然上述文章對有關受電弓的氣動特性進行了計算分析，但并沒有形成規律性的結論，與實驗數據對比證明其正確性的相關文獻也較少，所以對新研發的受電弓，仍然需要對其空氣動力學特性進行數值分析.

本文以最新研制的受電弓為研究對象，此款受電弓采用單碳滑板弓頭，與之前雙碳滑板弓頭相比，具有質量小、空氣動力性能好、燃弧率低、受流穩定性高等特點，同時對整體結構進行改進，提高結構部件疲勞壽命，比以往的受電弓更簡單、緊湊和穩定.對不同升弓高度下受電弓不同風速的氣動力進行數值模擬并進行受電弓抬升力的計算，與風洞試驗結果對比分析，為優化受電弓的空氣動力學特性提供技術支持.

1 計算模型概述

1.1 算法原理

本文采用的研究方法是基于計算流體動力學的數值計算.首先按照受電弓和風洞的實際尺寸等建立受電弓-風洞流場計算模型并進行網格劃分.在風洞中進行實驗時，受電弓周圍的氣流為三維、定常和不可壓縮流動，所以采用不可壓縮N-S以及k-ε兩方程湍流模型，對不同升弓高度下、不同風速受電弓的氣動力進行數值計算，并分析受電弓的空氣動力學特性.

1.2 三維幾何模型及網格劃分

本文以某種新型受電弓為研究對象，由于受電弓的三維幾何模型外形非常復雜，因此為了生成更高質量的網格，需要簡化其幾何結構.建模中應保留對受電弓氣動力特性有較大影響的形狀特征，以免過于簡化從而使得計算結果失去其應有的意義；相反，對于計算結果影響較小的幾何特征應盡可能地簡化掉.為了得到高質量的網格和降低網格規模，去掉了升弓裝置、凸臺等對計算結果影響甚微的零件，便于計算機快捷高效地進行模擬仿真.

簡化后的受電弓三維計算模型如圖1所示.在整個模擬仿真過程中，網格劃分有著極其重要的作用.對受電弓表面進行網格劃分時，由于受電弓某些結構尺寸較小，受電弓表面的網格尺寸需要進行合理處理.受電弓表面網格劃分細節如圖2和圖3所示.

圖1 受電弓幾何模型

圖2 弓頭表面網格劃分

圖3 連接處表面網格劃分

1.3 計算區域的確定及網格劃分

當進行受電弓氣動特性仿真計算時，流場區域達到一定范圍，計算區域與無限大流場的計算結果已非常接近.此時，繼續擴大流場區域已毫無實際意義[7].

在某風洞試驗場(3 m×3 m×14 m，受電弓距離進風口5 m)對受電弓進行了空氣抬升力測試，提供實驗的受電弓為機車用的實物受電弓，受電弓安裝在特殊設計的底架上，弓頭有拉繩懸掛并安裝有壓力傳感器，最大測試速度為320 km/h，通過專門的軟件獲得特定工況下的空氣抬升力數據.為了將數值計算結果與實驗結果相比較，建立與實驗中風洞尺寸完全一致的計算區域.根據實驗中風洞參數，選取如下流場域：外流場前端距模型前端5 m， 流場后端距模型尾部7 m， 流場寬度為3 m，高度為3 m，整個計算區域尺寸為3 m×3 m×14 m.計算區域模型如圖4所示.

圖4 計算區域模型

在對計算模型劃分網格時，采用以下方案：使用混合網格方法進行網格劃分，即使用結構網格和非結構網格.由于受電弓的結構復雜，因此在受電弓表面及附近區域采用非結構化網格，同時對受電弓表面的網格進行細化.在遠離受電弓的較大外部區域內，離受電弓距離越遠氣流流動影響越小，因此離受電弓越遠的網格可以劃分越大.此外，在距受電弓一定距離后，可以采用結構化網格.這樣可以減少網格數量、保證精度，同時減少計算時間.計算區域網格劃分如圖5所示，受電弓附近的網格已被細化，網格總數為800多萬.

圖5 計算區域網格劃分

1.4 邊界條件

由于是在有限的區域內進行受電弓外流場的數值計算，因此需要在區域邊界上給定邊界條件.基本思路是受電弓靜止不動，氣流以列車時速沿著列車前進方向的反向流動.計算邊界條件具體設置為：入口采用速度入口邊界，出口采用壓力出口邊界，計算區域的側面、頂面、底面采用無滑移壁面邊界條件.

2 工作高度2 800 mm計算結果及分析

利用計算流體力學軟件，仿真計算列車運行速度為160～320 km/h，受電弓在開口運行時，受電弓表面的壓力分布和速度分布情況，并計算弓頭、上臂桿、下臂桿和底座的氣動阻力和氣動升力.對氣動抬升力進行計算，計算方法參考文獻[8]，得到開口運行時的氣動抬升力仿真數據，并與實驗數據進行比較.由于篇幅所限，主要列舉列車運行速度320km/h，受電弓開口運行，受電弓的空氣動力特性的數值分析.

2.1 受電弓表面的壓力分布

受電弓開口狀態下的迎風側和背風側壓力分布如圖6所示.由圖6(a)可以看出，弓頭、上臂桿連接處和底座受到的表面壓力較大， 大部分區域分布在4 277～5 428 Pa范圍內.由圖6(b)可以看出，弓頭受到的表面壓力絕對值較大，大部分區域分布在-2 627～-1 476 Pa范圍內，背風側出現最小壓力值為-16 437 Pa.結合圖6可以看出，受電弓隨列車迎風運行時，由于迎風面空氣受擠壓，使受電弓迎風面周圍流場呈正壓狀態，背風面體現出較大的負壓，從而產生了壓差阻力.弓頭部件的正負壓差比較明顯，充分說明弓頭是氣動阻力的主要來源.由于臂桿前后方的壓力差，上臂桿會受到向上的空氣升力，下臂桿受到向下的空氣升力.

(a) 迎風面

2.2 受電弓各部件的氣動力

受電弓開口狀態下的氣動阻力和升力數據如表1所示，并繪制曲線如圖7所示.受電弓開口運行時各部件氣動阻力的絕對值隨著風速的增大而逐漸增大，其中弓頭的氣動阻力隨著風速的增大而增加幅度最大，基本保持速度每增加40 km/h，阻力增加約100 N. 下 臂 桿 的 氣 動阻力隨著風速的增大而增加幅度也較大，基本保持速度每增加40 km/h，阻力增加40 N.弓頭的氣動升力趨勢不明顯，上下臂桿產生的氣動升力方向相反，可相互抵消.明顯看出，弓頭受到風速的影響最大，其次是上臂桿和下臂桿.

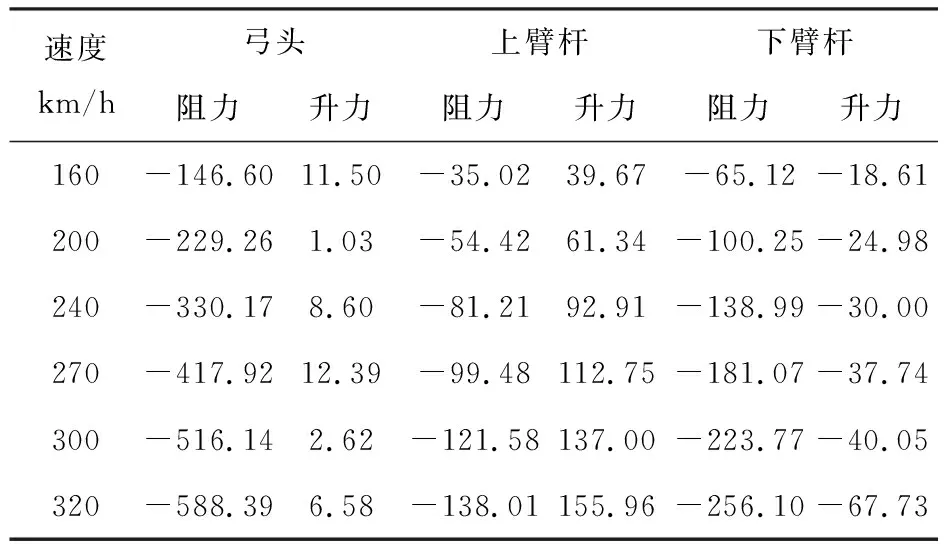
表1 受電弓開口運行各部件氣動力 N

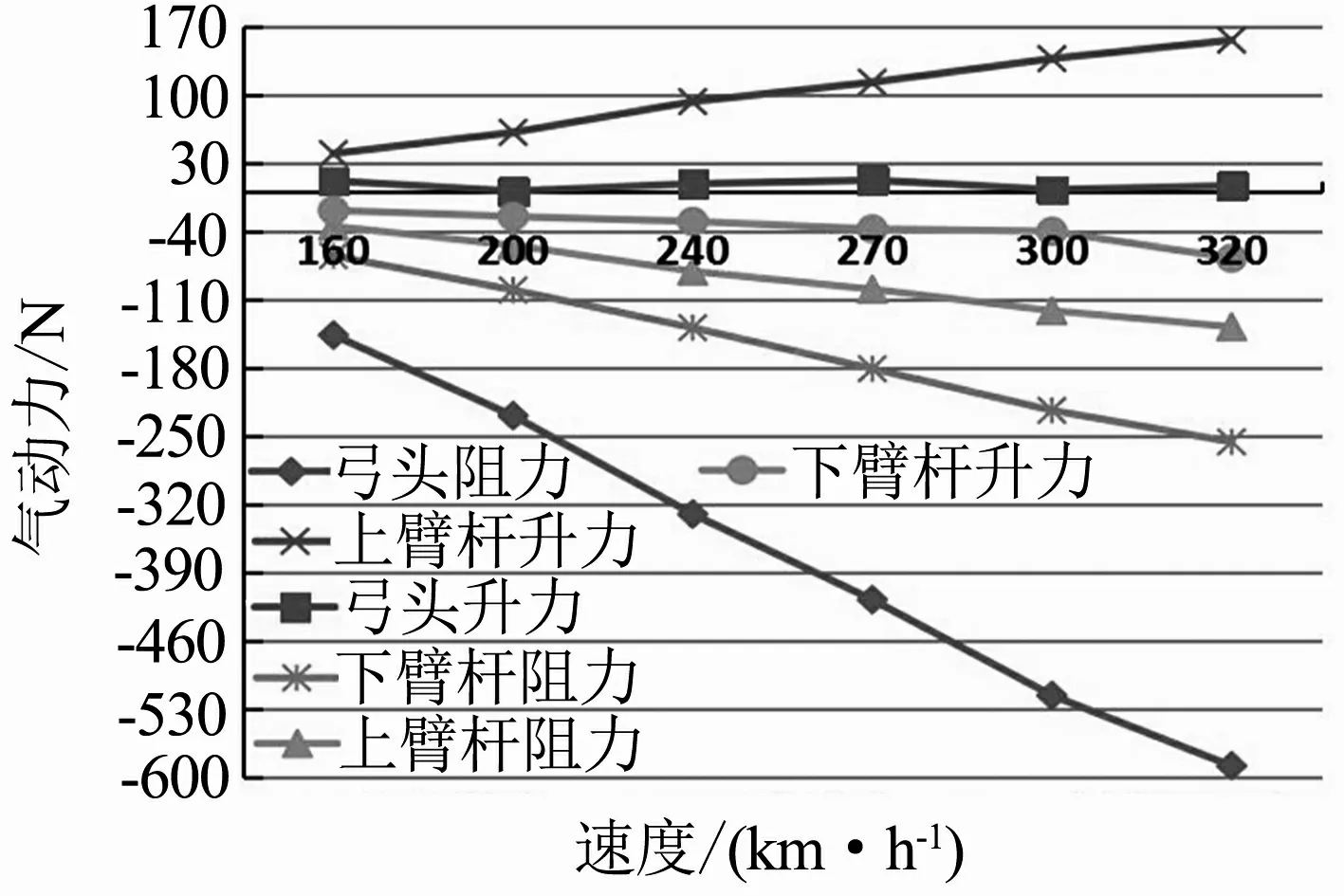
圖7 受電弓開口運行時各部件氣動力隨速度變化趨勢

2.3 受電弓氣動抬升力

受電弓開口狀態下的仿真計算數據與實驗數據對比如表2所示，繪制曲線如圖8所示.受電弓開口狀態下的計算仿真結果和實驗數據較接近，氣動抬升力隨列車速度的增加而不斷增大，基本保持速度每增加40 km/h，氣動抬升力增加30～40 N.實驗數據和仿真結果的變化規律較為一致，誤差保持在10%以內，說明本文數值計算結果具有一定可靠性.

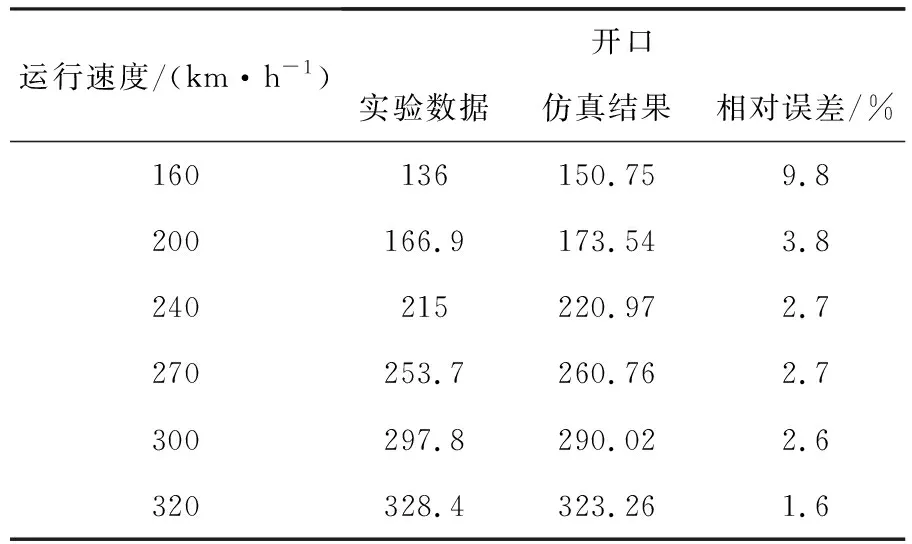
表2 受電弓開口運行氣動抬升力與實驗數據對比

圖8 受電弓開口運行時氣動抬升力隨速度變化趨勢

3 工作高度1 600 mm計算結果及分析

在受電弓工作高度2 800 mm仿真結果得到肯定后，對工作高度1 600 mm的受電弓進行仿真計算，與工作高度2 800 mm做對比分析.由于篇幅所限，主要列舉列車運行速度320 km/h，受電弓開口運行，受電弓的空氣動力特性的數值分析.

3.1 受電弓表面的壓力分布

受電弓開口狀態下的迎風側和背風側壓力分布如圖9所示.由圖9(a)可以看出，弓頭和上下臂桿連接處受到的表面壓力較大，大部分區域分布在4 287～5 447 Pa范圍內，迎風側出現最大壓力值5 447 Pa.由圖9(b)可以看出，上臂桿和下臂桿的連接處表面壓力絕對值較大，大部分區域分布在-3 883～-1 513 Pa范圍內，背風側出現最小壓力值為-16 594 Pa.

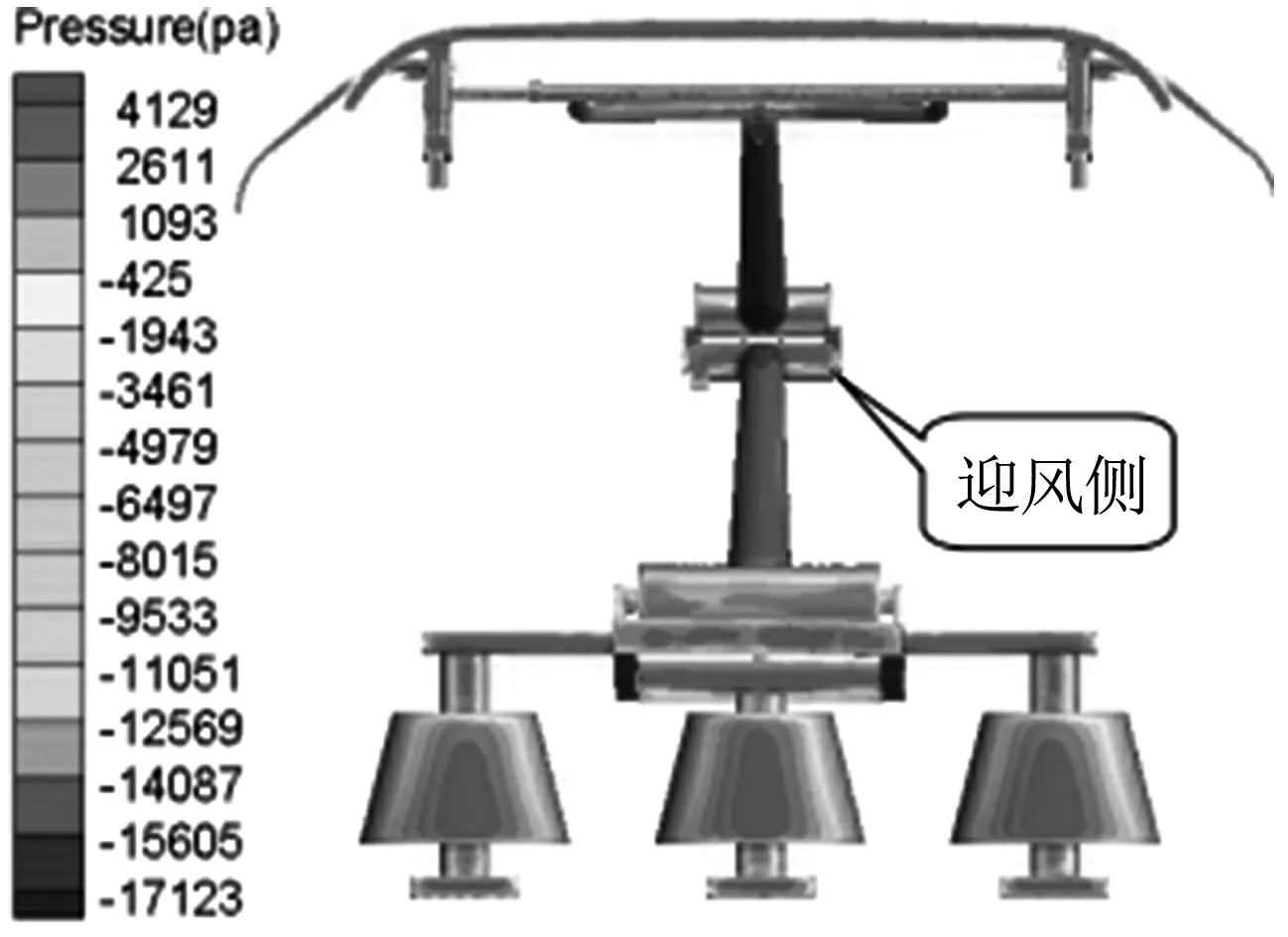
(a) 迎風面

3.2 受電弓各部件所受的氣動力

受電弓開口狀態下統計的氣動阻力和升力數據如表3所示，并繪制曲線如圖10所示.與上文工作高度2 800 mm氣動力對比分析，同一速度下，受電弓各部件氣動升、阻力隨工作高度減小而絕對值減小.但工作高度1 600 mm開口運行時各部件的氣動阻力和升力的絕對值隨著風速的增大也逐漸 增 大. 與 工 作 高度2 800 mm相似，弓頭的氣動阻力的增加幅度最大，基本保持速度每增加40 km/h，阻力增加約100 N.上下臂桿產生的氣動升力方向相反，可相互抵消.不同高度下，弓頭受到列車時速的影響最大，其次是上臂桿和下臂桿.

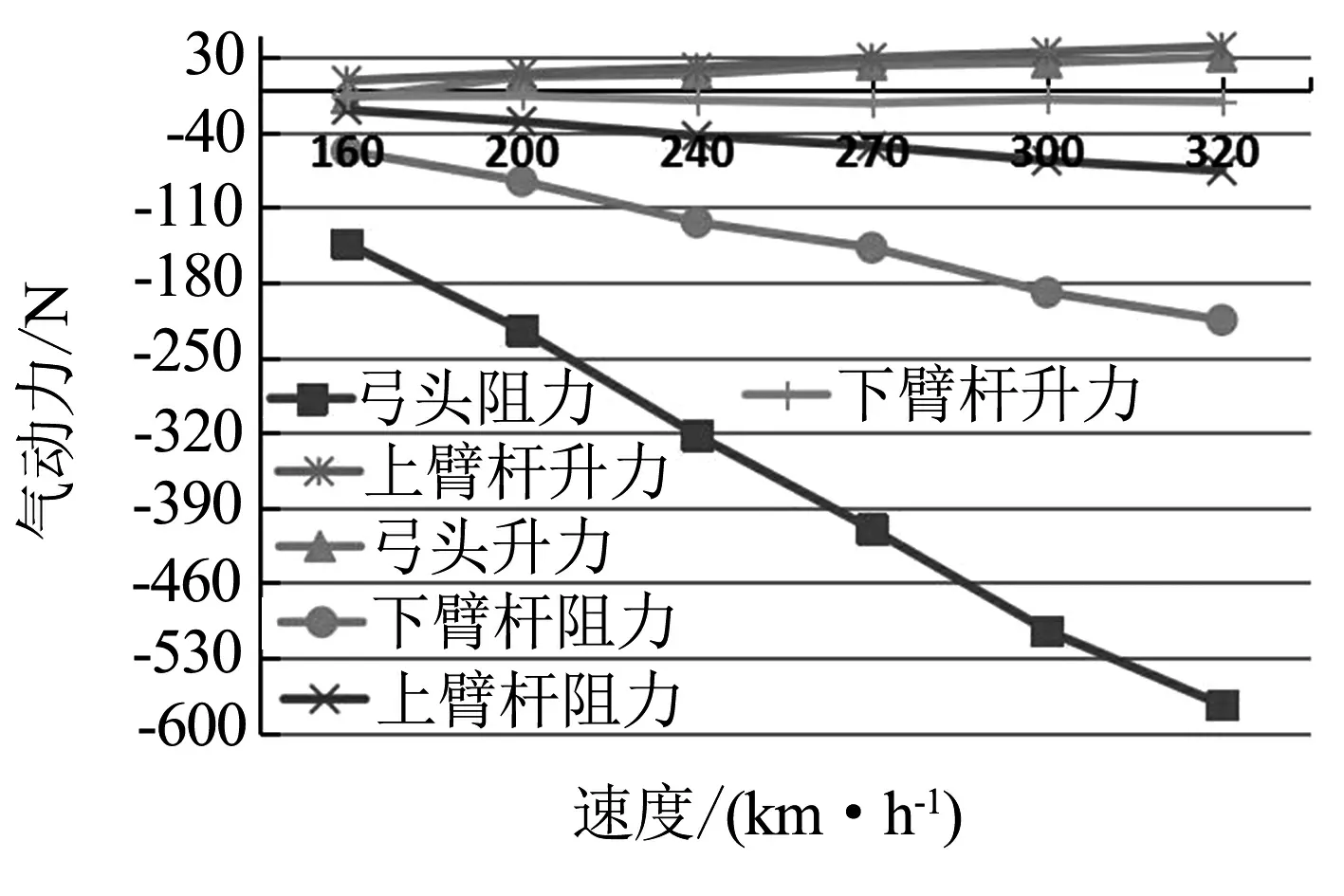
圖10 受電弓開口運行時各部件氣動力隨速度變化趨勢

3.3 不同高度下受電弓氣動抬升力對比分析

受電弓工作高度為2 800 mm和1 600 mm的開口狀態下的氣動抬升力數據對比如表4所示，繪制曲線如圖11所示.受電弓由工作高度2 800 mm降低至1 600 mm，同一速度下整弓的氣動抬升力隨著工作高度的減小而減小，但同一高度下氣動抬升力都隨著速度的增加而逐漸增大.其中工作高度為2 800 mm時氣動抬升力隨速度增加而增加幅度較大，速度每增加40 km/h氣動抬升力增加30 N.工作高度為1 600 mm時氣動抬升力隨速度增加而增加幅度較小，速度每增加40 km/h氣動抬升力增加10 N以內.

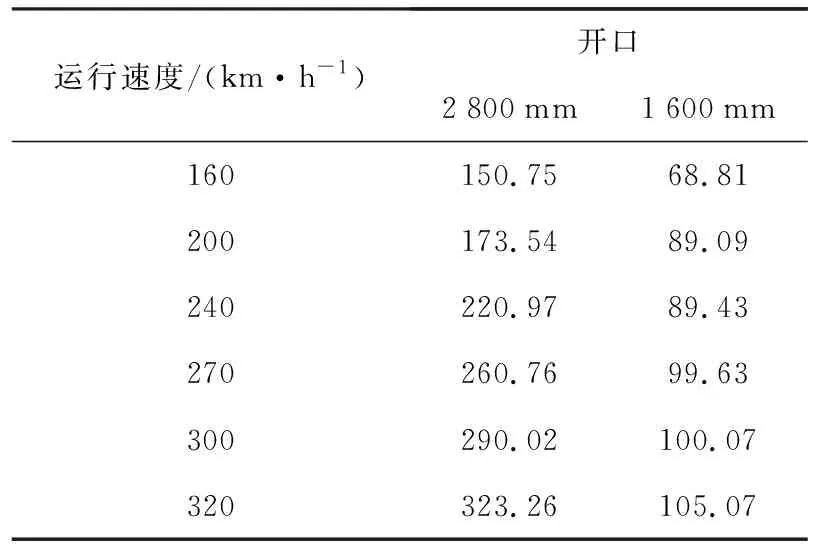
表4 受電弓不同高度下開口運行時氣動抬升力數據對比

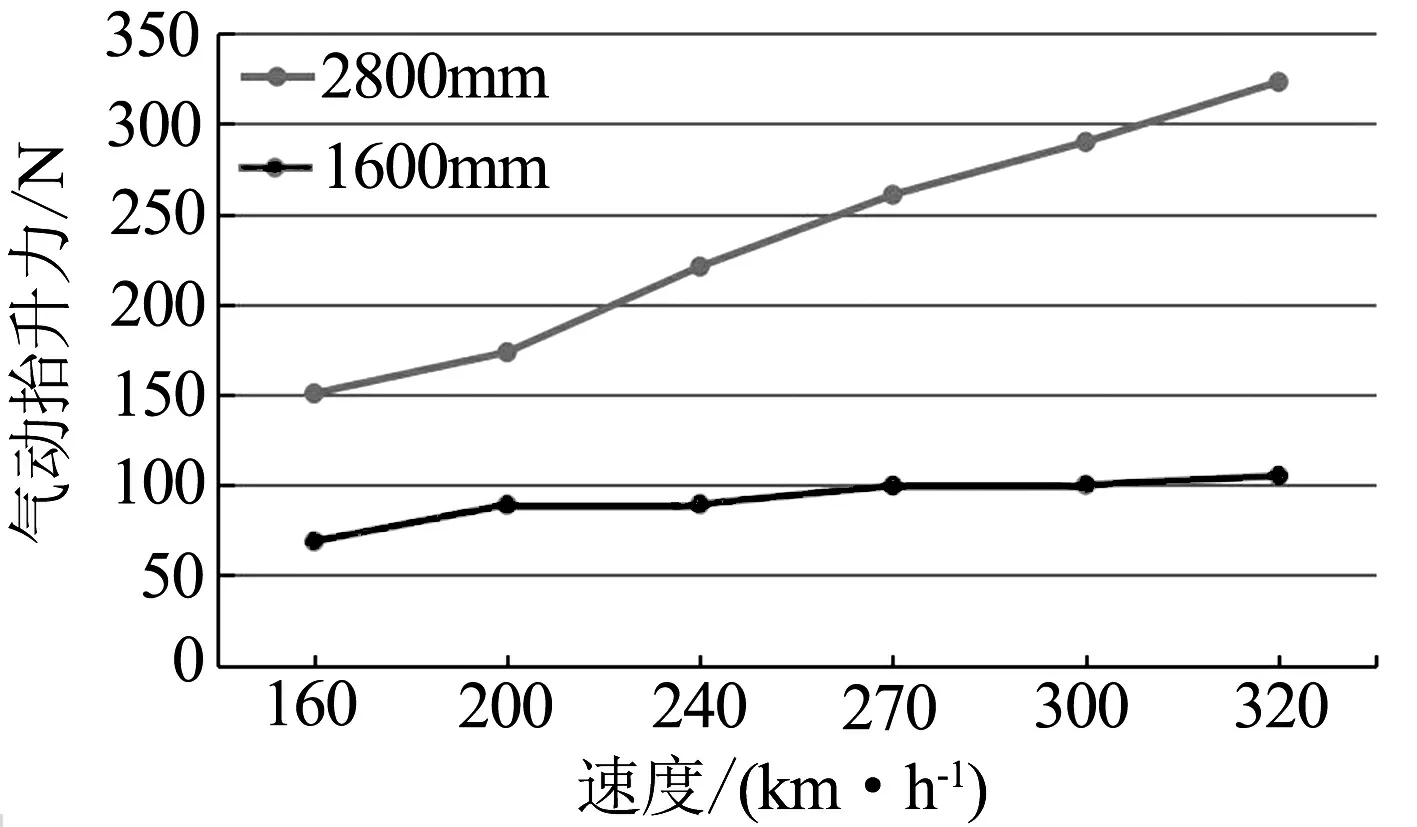
圖11 受電弓不同高度開口運行時氣動抬升力隨速度變化趨勢

4 結論

(1)在列車時速為160～320 km/m的條件下，對某新研制受電弓工作高度2 800 mm時開口工作狀態下的氣動流場進行了數值分析.根據數值計算所得的受電弓各部件的氣動力，計算得到工作高度為2 800 mm時受電弓6個列車時速下的抬升力.將仿真結果與實驗數據進行對比，仿真結果與實驗數據的變化規律一致，誤差保持在10%以內，說明本文數值計算結果具有一定可靠性;

(2)受電弓開口運行時，同一高度下，弓頭的氣動阻力隨著風速的增大而增加幅度最大，基本保持速度每增加40 km/h，阻力增加約100 N.上下臂桿產生的氣動抬升力方向相反，可相互抵消;

(3) 受 電 弓 由 工 作 高 度2 800 mm 降 低 至1 600 mm，受電弓各部件氣動升、阻力基本都隨著工作高度減小而絕對值減小，降幅基本保持在20 N以內.整弓的氣動抬升力也隨著工作高度的減小而減小，隨著速度的增加.降幅基本保持在60%以內.同一高度下整弓的氣動抬升力都隨著速度的增加而逐漸增大，工作高度2 800 mm時速度每增加40 km/h，氣動抬升力增加約30 N；工作高度1 600 mm時速度每增加40 km/h，氣動抬升力增加保持在10 N以內;

(4)弓頭是影響受電弓氣動特性最大的子部件，受電弓優化的重點在弓頭處，可以通過在弓頭處加裝導流板的方式來改善其空氣動力學特性.根據受電弓氣動特性分析，對企業受電弓優化具有一定的指導意義.